Атом физикасы: тарихи даму, атом құрылымы және кванттық түсініктер


1- лекция. Тақырыбы: Кіріспе. Атом, қатты дене, атом ядросының және қарапайым бөлшектер физикасының даму кезеңдері. . Микроәлем құбылыстарының өлшемдері
Лекция мақсаты: Студенттерге атом, қатты дене, атом ядросы туралы түсінік беру.
Лекция мәтіні (қысқаша)
Бізді қоршаған табиғаттағы заттар неден тұрады? Оларды табиғат қалай жасаған? Заттарды құрайтын ең кішкене бөлшек не деген сұрақтар ертеден қойылып келеді. Үлкен, зәулім таулар судың, желдің және вулкандық күштердің әсерінен бұзылып тасқа, ал тастардың өзі бара-бара шаңға айналады. Табиғат бөле алмайтын ең кішкене бөлшек бар маб бар болса ол не?
Ертедегі грек философтары Демокрит және Лепкип мұндай бөлшектер бар, олар «атомдар» деп есептеген. «Атом»-грек тілінде «бөлінбейтін» деген сөз. Атом қандай, оның түрі қандай деген сұрақ ғасырлар бойы жауапсыз қалды. Мүмкін атомдар кішкене шариктер шығар, немесе басқа формада ма? Ертедегі грек философы Анаксиманд әлемді төрт нәрсе - су, ауа, жер, от құрайтынын, ал олардың өзі атомдардан тұратынын айтқан. Алайда, ертедегі грек философтарының бұл ойлары эксперимент жүзінде дәлелденбей, тек болжам түрінде қалды да одан бергі ғасырларла көпке дейін атом туралы сөз болған жоқ.
Атом туралы ілімнің XVІІ- XVІІІ ғасырларда қайтадан дамуына химиялық элементтер туралы түсініктің пайда болуы, химиялық реакциялар кезінде зат массасының сақталуы, затты құрайтын элементтердің бір-бірінен айырмашылығының болуы, мысалы, судың құрамында сутегі мен оттегі болатыны және т. с. с. құбылыстар мен заңдылықтардың ашылуы үлкен әсерін тигізді. Сөйтіп, атомдар заттың ең кішкене бөлшектері, олар бір-бірімен қосылып заттың химиялық қасиетін сақтайтын кішкене бөлшек-молекула құрайтыны, ал молекулалар жиынтығынан бізді қоршаған заттар түзілетіні ашылды. XVІІІ ғасырда ұлы орыс ғалымы М. В. Ломоносов өзінің «Математикалық химияның элементтері» және тағы басқа еңбектерінде химиялық элементтер, күрделі және жай заттарды құрайтын бөлшектер туралы түсінік берген. Заттарды құрайтын бөлшектер екенін және олардың үнемі қозғалыста болатынын дәлелдеп, газдардың кинетикалық теориясының негізін қалады. Өкінішке орай М. В. Ломоносовтың бұл еңбектері де ұзақ уақыт ұмытылып, жабулы қалпында қалды.
Ағылшын ғалымы Дальтон 1804 ж. Еселік қатынас заңдылығын ашып, химиялық қосылыстардағы екі элементтің массалыры, қандай жолмен қосылғандарына байланыссыз, әрқашан тұрақты болатынын дәлелдеді. Бұдан қосылыстарға қатынасатын элементтер дискреттік бөлшектер ретінде, яғни атомдар түрінде болатыны дәлелденді, ал қосылыстар құрайтын әр түрлі элементтердің - атомдардың массасының да әр түрлі болатыны көрінді. Ал 1811 ж, ашылған Авогадро заңы молекула құралуы үшін, мысалы, аммиак молекуласында, сутегі үш атомды, су молекуласын құрау үшін сутегі екі атомды болуы керек екенін көрсетті. Сонымен қатар, Авогадро заңы температуралары мен қысымдары бірдей кез келген газдардың көлемінде молекулалар саны да бірдей екенін дәлелдеді. 1869 ж. Менделеев химиялық элементтердің периодтық системасын ашып, табиғаттағы әр элемент өзіне тән атомдық массасына байланысты система құрайтынын көрсетті.
Сонымен XІX ғасырдың екінші жартысында заттарды құрайтын ең кішкене бөлшек - атом әрі қарай бөлінбейтін дүниенің «кірпіші» деп есептелді. 1870 ж. ағылшын ғалымы Максвелл атом әрі қарай бөлінбейтін дене деп жазды. Бұл пікір XІX ғасырдың соңына дейін келді. Атом ілімі XІX ғасырдың аяғында ғана табиғатты зерттейтін физика, химия, математика ғылымдарының өріс алуына байланысты дамып, ілгерілей түсті. 1896 ж. радиоактивтіліктің, 1897 ж. катод сәулелерінде электронның ашылуы, анод сәулелерінің, яғни оң зарядталған бөлшектердің бар болуы атомның бөлінбейтін бөлшек деген ұғымына шек келтірді. Егер атом бөлінбейтін бөлшек болса, онда өз алдына өмір сүре алатын, теріс зарядты бөлшек - электрон қайдан пайда болды (электрон массасы ең жеңіл элемент, сутегі атомының массасынан 200 есеге жуық жеңіл) ? Ал электр бейтарап атом бөлінбейді десек онда атом деп есептеуге болмайтын теріс зарядталған кішкене бөлшек - электрон қайдан келді? Уран тұзы не себептен сәулелер шығарады және ол сәулелер қайдан шығады? деген және т. с. с. сұрақтар жауапсыз қалды.
Ендеше атом күделі болғаны ғой. Ал оның құрылымы қандай, құрамына қандай бөлшектер енеді және олар қалай орналасады деген сұрақтар пайда болды.
Бақылау сұрақтары:
- Атом деген сөздің мағынасы қандай?
- Атом жөніндегі алғашқы көзқарастар?
- Дальтон ашқан қатынастың аталуы?
- Атом құрамына қандай бөлшектер енеде?
2- лекция. Тақырыбы: Атом туралы кванттық түсініктер . Атом және молекулалар. Атомның периодтық қасиеттері. α-бөлшектердің шашырауы туралы Резерфорд тәжірибесі. . Атомның планетарлық-ядролық моделі. Резерфорд өрнегі. . Атом күйлерінің орнықтылығы және дискреттілігі.
Лекция мақсаты: Студенттерге атомның алғашқы модельдерін түсіндіру, Резерфорд өрнегімен таныстыру
 Лекция мәтіні (қысқаша)
Лекция мәтіні (қысқаша)
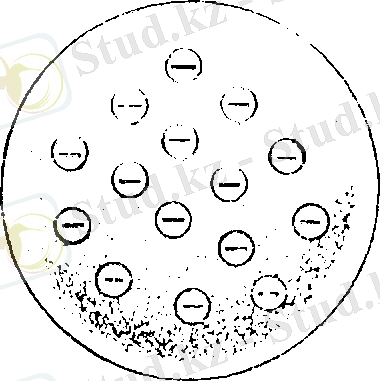
1900 жылы электрон барлық атомдардың құрамында болатыны анықталды. Атомның бірінші моделін 1902-1901 жж. Дж. Томсон ұсынған. Бұл модель бойынша oң
зарядталған біртекті атом массасына тербелмелі қозғалыста болатын теріс зарядты электрондар орналасқан, яғни атом бейнелеп көрсетсек «мейіз қосылған булка нан» сияқты (мейіз түйірлері
электрон ролін атқарады), оң заряд атомның бүкіл көлемін түгелдей жайлайды деген (1-сурет) . Бұл модель термоэлектрондық эмиссия кезінде электрондардың ытқып шығуын 1-сурет
атомның электромагниттік толқындарды шығаруын, иондардың пайда болу процестерін және т. с. с. құбылыстарды түсіндіре алды. Әрине, Томсон моделі атом туралы ілімнің дамуында белгілі роль атқарды.
Ағылшын ғалымы Резерфорд 1908-1911 жж. жүргізілген тәжірибелерінде атом ішіндегі зарядтың таралуын зерттеу отырып Томсон моделінің қате екенін дәлелдеді. Резерфорд тәжірибелерінде жұқа алтын фольга арқылы өткендегі
 -бөлшектердің шашырауын қарастырды (алтынның созымдылық қасиеті өте жоғары, одан өте жұқа фольга жасауға болады) . Тәжірибеде қолданылған фольга қалындығы -
-бөлшектердің шашырауын қарастырды (алтынның созымдылық қасиеті өте жоғары, одан өте жұқа фольга жасауға болады) . Тәжірибеде қолданылған фольга қалындығы -
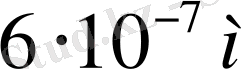 шамасында. Моноэнергетикалық, яғни энергиялары
шамасында. Моноэнергетикалық, яғни энергиялары
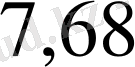 МэВ
МэВ
 -бөлшектердің көзі ретінде радиоактивтік препарат
-бөлшектердің көзі ретінде радиоактивтік препарат
 қолданылған.
қолданылған.
1909 ж. жүргізілген тәжірибелермен Резерфорд
 -бөлшектердің заряды оң, ал шамасы
2е
-ге тең, екенін тапқан еді,
-бөлшектердің заряды оң, ал шамасы
2е
-ге тең, екенін тапқан еді,
 -бөлшектердің шашырауы зерттейтін құралдың схемасы 2-суретте берілген,
-бөлшектердің шашырауы зерттейтін құралдың схемасы 2-суретте берілген,
 -бөлшектер көзінен шыққан бөлшектер қорғасын коллиматорлардан өтіп өте жіңішке шоқ ретінде
-бөлшектер көзінен шыққан бөлшектер қорғасын коллиматорлардан өтіп өте жіңішке шоқ ретінде
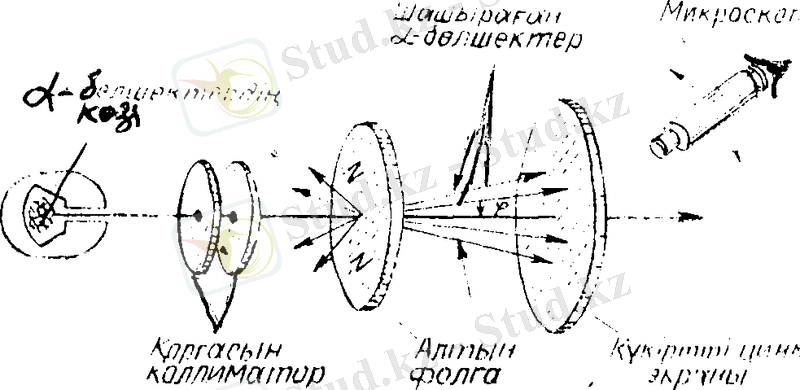
алтын фольгаға түседі (қорғасын
 -бөлшектерді жақсы жұтады) . Алтыннан шашыраған
-бөлшектерді жақсы жұтады) . Алтыннан шашыраған
 -бөлшектер күкіртті мырыш (цинк) жағылған экранға түскен. Экранға түскен әрбір бөлшек экранда жарықтың жылтылдауын (сцинтиляциясын) туғызады. Көптеген
-бөлшектер күкіртті мырыш (цинк) жағылған экранға түскен. Экранға түскен әрбір бөлшек экранда жарықтың жылтылдауын (сцинтиляциясын) туғызады. Көптеген
 -бөлшектер фольгадан өткенде өзінің әуелгі бағытын сақтаған, немесе әуелгі бағытынан кішкене
-бөлшектер фольгадан өткенде өзінің әуелгі бағытын сақтаған, немесе әуелгі бағытынан кішкене
 бұрышқа ауытқыған бөлшектер микроскоп экранына түседі.
бұрышқа ауытқыған бөлшектер микроскоп экранына түседі.
 -бөлшектер ауаның молекуласына соқтығыспас үшін құрал түгелімен вакуум ыдысқа орналастырылған. Шашыраған бөлшектердің аз ғана бөлігі
-бөлшектер ауаның молекуласына соқтығыспас үшін құрал түгелімен вакуум ыдысқа орналастырылған. Шашыраған бөлшектердің аз ғана бөлігі
 -қа, ал кейбіреулері тіпті
-қа, ал кейбіреулері тіпті
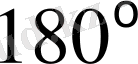 -қа жақын бұрышпен кері бұрылған (шамамен 20 000 бөлшектен біреуі) .
-қа жақын бұрышпен кері бұрылған (шамамен 20 000 бөлшектен біреуі) .
Алдын ала есептеулерге қарағанда, Томсон моделі бойынша
 -бөлшектер бастапқы бағытынан тек кішкене
-бөлшектер бастапқы бағытынан тек кішкене
 бұрышқа ауытқуы керек еді, себебі Томсон атомының ішіндегі электр өрісі әлсіз болуы керек, біркелкі зарядталған шардың электр өрісі оның бетінде максимал болып шардың центріне жақындаған сайын нольге дейін кемуі керек. Тәжірибелердің қорытындысына қарап, кейбір
бұрышқа ауытқуы керек еді, себебі Томсон атомының ішіндегі электр өрісі әлсіз болуы керек, біркелкі зарядталған шардың электр өрісі оның бетінде максимал болып шардың центріне жақындаған сайын нольге дейін кемуі керек. Тәжірибелердің қорытындысына қарап, кейбір
 -бөлшектердің үлкен бұрышқа шашырауын Томсон моделімен түсіндіруге мүмкіндік болмады. Бұл құбылысты түсіндіру үшін Резерфорд оң зарядталған бөлшектер алтын фольгадан өту жолында шама жағынан үлкен оң зарядқа және үлкен массалы денеге кездеседі де одан Кулон заңы бойынша кері тебіледі деп есептеді, яғни атомның оң заряды оның бүкіл көлемінде таралған емес, белгілі бір кішкене аймағына - ядроға жиналып, оның көлемі атомның көлеміне қарағанда анағұрлым кіші.
-бөлшектердің үлкен бұрышқа шашырауын Томсон моделімен түсіндіруге мүмкіндік болмады. Бұл құбылысты түсіндіру үшін Резерфорд оң зарядталған бөлшектер алтын фольгадан өту жолында шама жағынан үлкен оң зарядқа және үлкен массалы денеге кездеседі де одан Кулон заңы бойынша кері тебіледі деп есептеді, яғни атомның оң заряды оның бүкіл көлемінде таралған емес, белгілі бір кішкене аймағына - ядроға жиналып, оның көлемі атомның көлеміне қарағанда анағұрлым кіші.
Мұндай кішкене көлемнен
 -бөлшектердің шашырау ықтималдығы аз, сондықтан көптеген бөлшектер аз ғана бұрышқа шашырайды (3-сурет) . Ядроға тікелей тура келген бөлшек қайта тебіліп үлкен бұрышқа шашырайды.
-бөлшектердің шашырау ықтималдығы аз, сондықтан көптеген бөлшектер аз ғана бұрышқа шашырайды (3-сурет) . Ядроға тікелей тура келген бөлшек қайта тебіліп үлкен бұрышқа шашырайды.
 -бөлшектердің ядроға тию ықтималдығы өте аз, бірақ нольге тең емес. Ал атомның қалған көбірек бөлігін электрондар жайлайды. Олардың бүкіл теріс заряды ядроның оң зарядымен бейтараптанады. Электрон массасы өте аз болғандықтан
-бөлшектердің ядроға тию ықтималдығы өте аз, бірақ нольге тең емес. Ал атомның қалған көбірек бөлігін электрондар жайлайды. Олардың бүкіл теріс заряды ядроның оң зарядымен бейтараптанады. Электрон массасы өте аз болғандықтан
 -бөлшектердің қозғалысына әсер етпейді деп есептеген.
-бөлшектердің қозғалысына әсер етпейді деп есептеген.
Резерфорд
 -бөлшектердің оң заряды бар ядроның кулондық өрісінде ауытқуын теория жүзінде қарастырып, ядро зарядының шамасымен есептеген. 4-суретте
-бөлшектердің оң заряды бар ядроның кулондық өрісінде ауытқуын теория жүзінде қарастырып, ядро зарядының шамасымен есептеген. 4-суретте
 -бөлшектің
-бөлшектің
 заряды бар ядродан ауытқуы көрсетілген. Шашырау теориясы бойынша нысына қашықтығы дегеніміз, егер
заряды бар ядродан ауытқуы көрсетілген. Шашырау теориясы бойынша нысына қашықтығы дегеніміз, егер
 -бөлшектің тебу күші болмаса, ядроға ең жақын келетін ара қашықтық
р.
Кулон күші әсерінен кейбір
-бөлшектің тебу күші болмаса, ядроға ең жақын келетін ара қашықтық
р.
Кулон күші әсерінен кейбір
 -бөлшек өзінің траекториясын өзгертіп АВС сызығының бойымен, яғни гипербола бойымен қозғалады, белгілі бір
-бөлшек өзінің траекториясын өзгертіп АВС сызығының бойымен, яғни гипербола бойымен қозғалады, белгілі бір
 бұрышына шашырайды. Әсер етуші Кулон күшінің шамасы:
бұрышына шашырайды. Әсер етуші Кулон күшінің шамасы:
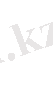
4-сурет
(1)
Мұндағы
 -
-
 -бөлшектің заряды,
-бөлшектің заряды,
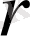 -
-
 -бөлшек пен ядроның центрлерінің ара қашықтығы,
-бөлшек пен ядроның центрлерінің ара қашықтығы,
 - электрлік тұрақты. Нысана ара қашықтығы
р
өзгергенде шашырау бұрышы
- электрлік тұрақты. Нысана ара қашықтығы
р
өзгергенде шашырау бұрышы
 әр түрлі болады. Ал, ядроға тура бағытталған
әр түрлі болады. Ал, ядроға тура бағытталған
 -бөлшектің нысана қашықтығы
р=0
болады да, бір
D
нүктесіне дейін келіп, ең минимал
r
0
ара қашықтығында кейін бұрылады.
-бөлшектің нысана қашықтығы
р=0
болады да, бір
D
нүктесіне дейін келіп, ең минимал
r
0
ара қашықтығында кейін бұрылады.
 -бөлшектің ядромен әсерлесуін сипаттау үшін
-бөлшектің ядромен әсерлесуін сипаттау үшін
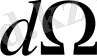 денелік бұрышпен шашыраған конустық бетпен шектелген
денелік бұрышпен шашыраған конустық бетпен шектелген
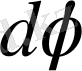 бұрышы бар денелік бұрыш ішіндегі
бұрышы бар денелік бұрыш ішіндегі
 -бөлшек санын білу қажет. 5-суретте осындай кішкене бұрышпен шашыраған
-бөлшек санын білу қажет. 5-суретте осындай кішкене бұрышпен шашыраған
 -бөлшектер экрандағы
С
сақинасына, ал Резерфорд тәжірибесінде микроскоп экранына түсіп жылтылдау туғызады.
-бөлшектер экрандағы
С
сақинасына, ал Резерфорд тәжірибесінде микроскоп экранына түсіп жылтылдау туғызады.
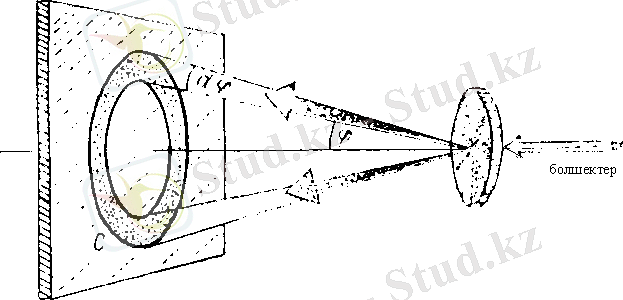
Фольгаға бағытталған бүкіл
 -бөлшектердің тығыздығы, яғни бірлік уақытта бірлік ауданға түсетін бөлшек саны н
0
, ал кішкене ғана элементар
-бөлшектердің тығыздығы, яғни бірлік уақытта бірлік ауданға түсетін бөлшек саны н
0
, ал кішкене ғана элементар
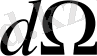 денелік бұрыш ішінде шашыраған
денелік бұрыш ішінде шашыраған
 -бөлшек саны
dn
болса делік. Осы жалпы нысанаға бағытталған
-бөлшек саны
dn
болса делік. Осы жалпы нысанаға бағытталған
 -бөлшектердің ішінен
-бөлшектердің ішінен
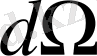 денелік бұрышының ішінде шашыраған
денелік бұрышының ішінде шашыраған
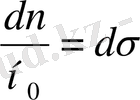 бөлігін алсақ, бұл шашыраудың эффективтік қимасы деген шаманы береді. d
бөлігін алсақ, бұл шашыраудың эффективтік қимасы деген шаманы береді. d
 атом физикасында жиі қолданылатын шама, өлшем бірлігі - м
2
, яғни өлшемі аудан өлшемдей. Атом физикасында көбінесе қолданылатын өлшем - барн (б), 1б =10
-20
м
2
. эффективтік қима шашырату центрінің ерекшелігімен сипатталады. Сонда, Резерфорд бойынша шашырау теориясына сүйенсек,
атом физикасында жиі қолданылатын шама, өлшем бірлігі - м
2
, яғни өлшемі аудан өлшемдей. Атом физикасында көбінесе қолданылатын өлшем - барн (б), 1б =10
-20
м
2
. эффективтік қима шашырату центрінің ерекшелігімен сипатталады. Сонда, Резерфорд бойынша шашырау теориясына сүйенсек,
 -бөлшек пен ядроны нүктелі оң зарядтар, олар бір-біріне Кулон заңы бойынша әсер етеді деп есептесе,
-бөлшек пен ядроны нүктелі оң зарядтар, олар бір-біріне Кулон заңы бойынша әсер етеді деп есептесе,
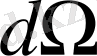 бұрышының ішіндегі шашыраған
бұрышының ішіндегі шашыраған
 -бөлшектер санын табуға мүмкіндік болады:
-бөлшектер санын табуға мүмкіндік болады:
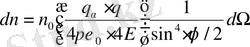 , (2)
, (2)
мұндағы Е -
 -бөлшектің жалпы энергиясы. (2) формуласы Резерфорд формуласы деп аталады. (2) формуласын өзгертіп, келесі түрде жазамыз:
-бөлшектің жалпы энергиясы. (2) формуласы Резерфорд формуласы деп аталады. (2) формуласын өзгертіп, келесі түрде жазамыз:
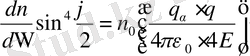 . (3)
. (3)
Тәжірибеде қарастырған
 -бөлшектер моноэнергетикалық болғандықтан, (3) формуласындағы
-бөлшектер моноэнергетикалық болғандықтан, (3) формуласындағы
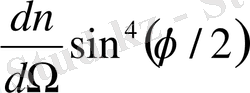 шамасы тұрақты болуы керек. Оқушылардың Гейгер мен Марсденнің жүргізген тәжірибелерінің нәтижесінде Резерфорд формуласының дұрыстығы дәлелденді. Мысалы, тәжірибенің бір сериясында 150 000 жылтылдау тіркелген, соның нәтижелерін төменгі таблицада қарастырамыз:
шамасы тұрақты болуы керек. Оқушылардың Гейгер мен Марсденнің жүргізген тәжірибелерінің нәтижесінде Резерфорд формуласының дұрыстығы дәлелденді. Мысалы, тәжірибенің бір сериясында 150 000 жылтылдау тіркелген, соның нәтижелерін төменгі таблицада қарастырамыз:
1-таблица. Алтын фольгадан
 -бөлшектердің шашырауы.
-бөлшектердің шашырауы.
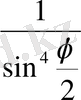
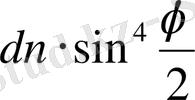
150
135
105
75
45
15
1, 15
1, 38
2, 53
7, 25
46, 6
3445
33
43
70
211
1435
132000
29
31
28
29
31
38
Таблицадан шашырау бұрышы
 өзгеруіне байланысты
өзгеруіне байланысты
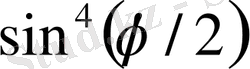 мөлшері 3000 есе өзгергеннің өзінде
мөлшері 3000 есе өзгергеннің өзінде
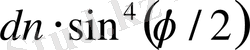 көбейтіндісі шамамен тұрақты екені көрінеді. Ал егер Томсон моделі бойынша оң заряд атомның бүкіл көлеміне таралған деп есептесек, мұндай заңдылық болмаған болар еді. Міне, сонымен Резерфордтың атомның бүкіл оң заряды ядроға жиналған деген тұжырымы дұрыс болып шықты.
көбейтіндісі шамамен тұрақты екені көрінеді. Ал егер Томсон моделі бойынша оң заряд атомның бүкіл көлеміне таралған деп есептесек, мұндай заңдылық болмаған болар еді. Міне, сонымен Резерфордтың атомның бүкіл оң заряды ядроға жиналған деген тұжырымы дұрыс болып шықты.
Тәжірибелерін қорытындылай келе Резерфорд атомның ядролық моделін ұсынды, оны кейде атомның планетарлық моделі деп атайды. Ол бойынша атом оң зарядталған ядродан және ядроны айналып қозғалатын электрондардан тұрады. Атомның бүкіл дерлік массасы ядроға шоғырланған. Резерфорд формуласын пайдаланып ең бірінші рет атом ядросының зарядын табу мүмкіндік болды. Әр түрлі металдармен істелген тәжірибелердің нәтижесінде (2) формуладағы
 екені дәлелденді,
екені дәлелденді,
 -Менделеев таблицасындағы элементтің реттік номері,
е
-электрон заряды, яғни периодтық системадағы элементтер номерінің физикалық мағынасы түсіндірілді. Ал, атом негізінен бейтарап болғандықтан ядроның оң зарядының шамасы
-Менделеев таблицасындағы элементтің реттік номері,
е
-электрон заряды, яғни периодтық системадағы элементтер номерінің физикалық мағынасы түсіндірілді. Ал, атом негізінен бейтарап болғандықтан ядроның оң зарядының шамасы
 болса, атомдағы электрон саны
болса, атомдағы электрон саны
 -ке тең болуы керек.
-ке тең болуы керек.
4-суреттегідей
 -бөлшектіңядроға тура бағытталған (
-бөлшектіңядроға тура бағытталған (
 ) жағдайын қарастырса, ядроның мөлшерін шамалауға болады, яғни
) жағдайын қарастырса, ядроның мөлшерін шамалауға болады, яғни
 -бөлшек пен ядроның ең жақындасатын минимал ара қашықтығы
-бөлшек пен ядроның ең жақындасатын минимал ара қашықтығы
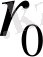 шамамен ядоның радиусына тең деп алуға болады.
шамамен ядоның радиусына тең деп алуға болады.
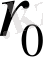 -дің сандық мәнін шамалау үшін
-дің сандық мәнін шамалау үшін
 -бөлшектің ядромен орталық соқтығысуы қарастырамыз, шашырау бұрышы
-бөлшектің ядромен орталық соқтығысуы қарастырамыз, шашырау бұрышы
 -қа тең деп аламыз. Энергияның сақталу және айналу заңы бойынша
-қа тең деп аламыз. Энергияның сақталу және айналу заңы бойынша
 -бөлшектің ядромен ең жақын ара қашықтыққа келгендегі кинетикалық энергиясы ядромен әсерлесудің потенциалдық энергиясына айналады:
-бөлшектің ядромен ең жақын ара қашықтыққа келгендегі кинетикалық энергиясы ядромен әсерлесудің потенциалдық энергиясына айналады:
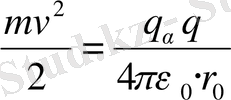 (4)
(4)
мұндағы
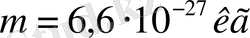
 -бөлшектің массасы,
-бөлшектің массасы,
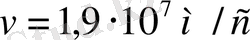 - оның ядродан алыстағы бастапқы жылдамдығы, алтынның Менделеев таблицасындағы номері
- оның ядродан алыстағы бастапқы жылдамдығы, алтынның Менделеев таблицасындағы номері
 , электрон заряды
, электрон заряды
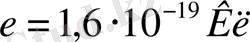 , ал
, ал
 ,
,
 ; сонда (4) формуласынан:
; сонда (4) формуласынан:
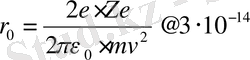 м. (5)
м. (5)
Міне, бұдан, алтын атом ядросының мөлшері табылған
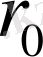 шамасынан кем болуы керек. Қазіргі өлшеулер бойынша ядро радиусы 10
-15
м, ал атом радиусы шамамен 10
-10
м, ендеше ядро атомнан 100 000 есе кіші.
шамасынан кем болуы керек. Қазіргі өлшеулер бойынша ядро радиусы 10
-15
м, ал атом радиусы шамамен 10
-10
м, ендеше ядро атомнан 100 000 есе кіші.
Атом ядросының массасы атом массасына тең деп алуға болады, себебі электрон массасы ядро массасына қарағанда шамамен мың есе аз болады. Ядро массасы мен радиусынбілсе, ядро « затының» тығыздығын табуға болады. Мысалы, сутегі атомының массасы
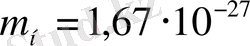 кг,
кг,
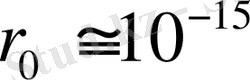 м, сонда ядро тығыздығы:
м, сонда ядро тығыздығы:
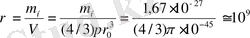 т/см
3
т/см
3
Ядро тығыздығы өте үлкен шама екен: 1 см 3 көлемде миллиард тонна.
Әрине, атомның Резерфорд моделі атом ілімінің дамуына үлкен әсер тигізді, атом табиғатын дұрыс түсінуге мүмкіндік берді. Бірақ Резерфорд моделінің классикалық электродинамика тұрғасынан елеулі кемшіліктері болды. 1) Электрон ядроны айналып қозғалғанда, оның қозғалысы үдемелі қозғалыс болғандықтан, ол үнемі электромагниттік энергия шығаруы тиіс, яғни электромагниттік толқын шығаруы керек, ал олай болса, электрон энергиясы азая береді. Электрон мен ядро арасы жақындай беріп, аз уақыт өткенде электрон ядроға құлап түсуі тиіс. Атом, бұзылуы керек. Ал күнделік тәжірибеден атом өте берік система екені белгілі. 2) Электрон ядроға жақындай берген сайын айналу периоды үздіксіз кеми береді. Осы кездегі шығарылған электромагниттік толқындардың жиілігі үздіксіз артып отырады. Сөйтіп, атомның шығарған электромагниттік толқын спектрі үздіксіз болуға тиіс. Өмірде атомның шығарған спектрі үздікті, сызықтық спектр болып табылады. Мысалы, сутегі атомының спектрлері - сызықтық спектрлер.
Бақылау сұрақтары:
- Дж. Томсон ұсынған атом моделі қандай?
- Резерфорд тәжірібісін түсіндіріңіз?
- Не үшін алтын фольга қолданылды?
- Резерфорд формуласын жазыңыз?
- Резерфорд тәжірибесінде радиоактивті препарат ретінде не қолданды?
3- лекция. Тақырыбы: Энергияның деңгейлері және оларды қоздыру әдістері. Шағылысу және жұтылу спектрлерінің жалпы сипаттамасы. Спектрлердің түрлері. Сутегі атомының спектрлік сериясы. . Бор постулаттары. . Атомның энергетикалық деңгейлері. Сутегі атомы туралы Бор теориясы. Сутегі тәріздес атомдардың спектрлік сериясы. Франк-Герц тәжірибесі. Бор теориясын нақтылы мағлұматтармен салыстыру. Бор теориясының қайшылықтары.
Лекция мақсаты: Студенттерге спектр түрлерін таныстыру, Бор постулаттарын түсіндіру.
Лекция мәтіні (қысқаша)
Шыны түтіктегі төменгі қысымдағы бір атомды газ арқылы (
Н
) электр тогын өткізген кезде газ атомдары электромагниттік толқындар, яғни жарық сәулелерін шығарады. Егер шыққан сәулелерді спектроскоп арқылы қарайтын болсақ, жарық сәулесі түрлі -түсті спектрлік сызықтар түрінде көрінеді. Сутегі атомының шығаратын спектрі
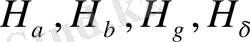 және т. с. с. белгіленеді. Бұл сызықтарды 1885 ж. швейцар ғалымы И. Бальмер ашқан, сондықтан оларды Бальмер сериясы деп атайды. Олардың төртеуі көрінетін аймақта, ал қалғандары спектрдің көрінбейтін ультракүлгін аймағында орналасқан. Небәрі Бальмер сериясында елуге жуық сызықтар бар. Бальмер сутегі атомының шығаратын спектрінің толқын ұзындықтарын келесі формула бойынша есептеуге болатынын тапты:
және т. с. с. белгіленеді. Бұл сызықтарды 1885 ж. швейцар ғалымы И. Бальмер ашқан, сондықтан оларды Бальмер сериясы деп атайды. Олардың төртеуі көрінетін аймақта, ал қалғандары спектрдің көрінбейтін ультракүлгін аймағында орналасқан. Небәрі Бальмер сериясында елуге жуық сызықтар бар. Бальмер сутегі атомының шығаратын спектрінің толқын ұзындықтарын келесі формула бойынша есептеуге болатынын тапты:
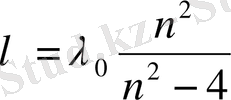 (1)
(1)
мұндағы
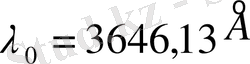 -тұрақты шама, ал
-тұрақты шама, ал
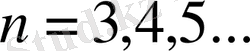 бүтін сандар. Мысалы,
бүтін сандар. Мысалы,
 деп алсақ, онда
деп алсақ, онда
 сызығының толқын ұзындығын табамыз, ал
сызығының толқын ұзындығын табамыз, ал
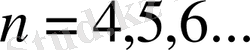 мәндерін алсақ
мәндерін алсақ
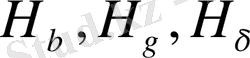 және т. с. с. толқын ұзындықтары табылады. (1) формуласындағы
және т. с. с. толқын ұзындықтары табылады. (1) формуласындағы
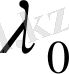 тұрақты шама
тұрақты шама
 жағдайда толқын ұзындығы
жағдайда толқын ұзындығы
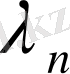 -нің шегі
-нің шегі
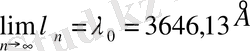 (2)
(2)
Егер жарықтың толқын ұзындығы
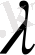 , жылдамдығы
, жылдамдығы
 және жиілігі
және жиілігі
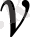 арасындағы байланысты
арасындағы байланысты
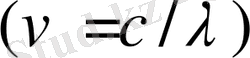 ескерсек, (1) Бальмер формуласын ыңғайлы түрге келтіруге болады.
ескерсек, (1) Бальмер формуласын ыңғайлы түрге келтіруге болады.
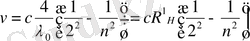 (3)
(3)
мұндағы
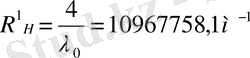 -сутегі спектрлері үшін тұрақты шама-Ридберг тұрақтысы, көпшілігінде оны
-сутегі спектрлері үшін тұрақты шама-Ридберг тұрақтысы, көпшілігінде оны
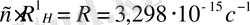 түрінде қолданып, (3) формуласын бвлай жазамыз:
түрінде қолданып, (3) формуласын бвлай жазамыз:
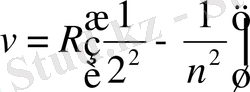 (4)
(4)
Атом туралы ілімнің өркендеуінде Бальмер формуласы үлкен роль атқарды. Сутегі атомы спектрінің инфрақызыл бөлігінде Ф. Пашен тағы да серия сызықтарын тапты. Ол сериялар келесі формуламен анықталады:
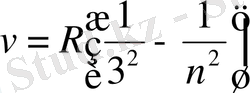 (5)
(5)
мұнда
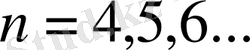 .
.
Ғалымдар сутегі атомының спектрлерін зерттеп, алшақ жатқан инфрақызыл және ультракүлгін облыстарында қосымша серияларды тапты. Олар Лайман сериясы:
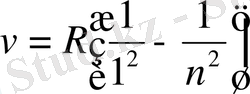
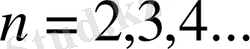 (6)
(6)
Брэкет сериясы
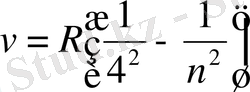 мұнда
мұнда
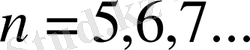 (7)
(7)
Пфунд сериясы
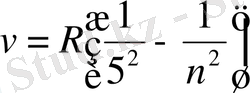 мұнда
мұнда
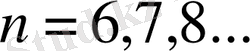 (8)
(8)
Хэмфри сериясы
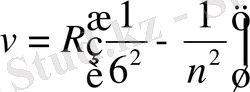 мұнда
мұнда
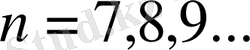 (9)
(9)
Ридберг сериялы формулаларды бір жүйеге келтіріп, барлық сериялар үшін біріккен формула шығарды:
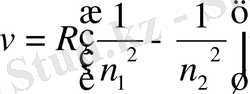 (10)
(10)
Мұндағы
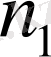 -бірден басталған бүтін сандар қатарын түзеді, ал
-бірден басталған бүтін сандар қатарын түзеді, ал
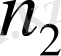 сол қатардағы
сол қатардағы
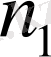 +1-ден басталған мәндерге тең. 1908 жылы В. Ритц спектрлік сериялар үшін өзінің комбинациялық принципін ұсында. Бұл принцип бойынша кез келген атомның шығару спектрінің жиілігін екі термнің айырымы түрінде беруге және сол атомның шығару спектрінің жиілігін осы термдерден әр түрлі комбинациялар құра отырып, тауып алуға болады деген:
+1-ден басталған мәндерге тең. 1908 жылы В. Ритц спектрлік сериялар үшін өзінің комбинациялық принципін ұсында. Бұл принцип бойынша кез келген атомның шығару спектрінің жиілігін екі термнің айырымы түрінде беруге және сол атомның шығару спектрінің жиілігін осы термдерден әр түрлі комбинациялар құра отырып, тауып алуға болады деген:
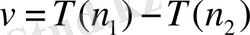 (11)
(11)
Мұнда
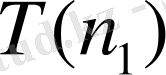 және
және
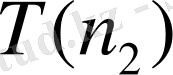 функциялары үшін спектрлік термдер деген ұғымдар енгізген. Берілген серия үшін
функциялары үшін спектрлік термдер деген ұғымдар енгізген. Берілген серия үшін
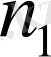 тұрақты шама, ал
тұрақты шама, ал
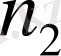 айнымалы. Мысалы, Бальмер сериясы үшін
айнымалы. Мысалы, Бальмер сериясы үшін
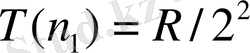 , ал
, ал
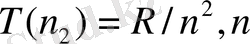 -шексіз өскенде
-шексіз өскенде
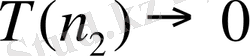 , яғни Бальмер сериясы өзінің шегіне ұмтылады:
, яғни Бальмер сериясы өзінің шегіне ұмтылады:
 .
.
Жоғарыда келтірілген (4), (5), (6), (7), (8), (9), (10), (11) сериялық формулалары - тәжірибеден алынған эмпирикалық формулалар. Олар көп уақытқа дейін теория жүзінде негізделіп дәлелденбеді. Сериялық формулалардың түрлері, олардың құрамындағы бүтін сандардың таң қаларлық қайталануы, Ридберг тұрақтысының универсалдығы, бұл формулалардың терең физикалық мағынасы бар екенін көрсетеді. Бірақ оны классикалық физика тұрғысынан түсіндіру мүмкін болмады. Міне, атомның Резерфорд моделінің қиыншылықтарына, классикалық электромагниттік теория тұрғысынан түсініксіз, электромагниттік сәуле шығарудың спектрлік термдерге байланыстылығы қосылды.
1913 ж. Дания ғалымы Бор классикалық физиканың теориясынан бөлек атом теориясын ұсынды. Ол Резерфорд атом моделі мен атомның спектр шығару жұту процестерін біріктіретін идеяны алды. Бор тұжырымы бойынша классикалық электродинамика заңдылықтарын атом ішіндегі процестерге қолдануға болмайды. Атом ішіндегі процестер Планктың кванттық теориясының заңдылықтарына бағынуға тиіс. Бор теориясында классикалық физикадан алынған көптеген ұғымдар бар еді, мысалы, электрон орбитасы, траекториясы туралы түсініктер және т. с. с. Бор атом ішіндегі электронның қозғалу заңдылықтарын көрсету үшін классикалық физиканың ұғымдарын толықтырды. Міне, осылай толықтырылған классикалық ұғымдар ең қарапайым система - сутегі атомының спектрлерінің орналасу заңдылықтарын дұрыс түсіндіре білді. Бор теориясын тек қана сутегі атомының күйін сипаттап қоймай, сонымен қатар сутегі атомына ұқсас системаларға да қолдануға болатынын көрсетті. Мысалы, мұндай системалар:
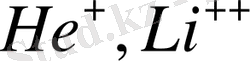 және т. с. с.
және т. с. с.
Бірақ Бор жүйелі атом теориясын берген жоқ, ол жаңа теорияның негізгі қағидаларын постулаттар түрінде тұжырымдады, сонымен бірге классикалық физиканың заңдарынан да қол үзген жоқ, жаңа постулаттар классикалық физикада рұқсат етілген қозғалысқа кейбір шектеулер ғана қойды. Осыған қарамастан, Бор теориясының табысы айтарлықтай болып, кейіннен микробөлшектердің теориясы - кванттық механиканың шығуына себепші болды.
Бор өз ойын келесі постулаттар түрінде берді:
І постулат. Атомдық система тек ерекше стационар немесе кванттық күйлерде ғана болады, олардың әрқайсысына белгілі бір энергия сәйкес келеді. Стационар күйде атом сәуле шағармайды.
Бұл постулат классикалық электродинамика заңына қайшы. Себебі, ядроны айналғанда электрон қозғалысы үдемелі қозғалыс, ал үдемелі қозғалыстағы электрон электромагниттік толқын шығаруы және электрон энергиясы кез келген мәнге ие болуы керек.
ІІ постулат. Атмо энергиясы көп
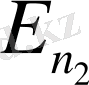 стационар күйден энергиясы аз
стационар күйден энергиясы аз
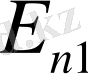 стационар күйге өткенде сәуле (фотон) шығарады. Шығарылған фотонның энергиясы стационар күйлердің энергияларының айырымына тең:
стационар күйге өткенде сәуле (фотон) шығарады. Шығарылған фотонның энергиясы стационар күйлердің энергияларының айырымына тең:
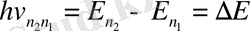 (1)
(1)
ал шығарылған сәуленің жиілігі
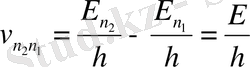 (2)
(2)
Ал егер атом фотонды жұтатын болса, ол энергиясы аз
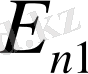 күйден энергиясы көп
күйден энергиясы көп
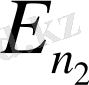 күйге өтеді (ядроға жақын орбитадан ядродан алыс орбитаға өтеді) .
күйге өтеді (ядроға жақын орбитадан ядродан алыс орбитаға өтеді) .
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz