Қатты денелердің беріктілігі мен жарамдылық мерзімі: статикалық және кинетикалық концепциялар, сынау әдістері


Беріктілік проблемаларды шешуде статикалық және кинетикалық көзқарастар.
Жоспары: 1. Ақауы жоқ идеал дененің морт қирауы.
2. Гриффитс-Иоффе теориясы.
3. Материалдың беріктілігіне зерттеу жүргізу.
4. Қатты денелердің жарамдылық мерзімі.
Лекция мақсаты:
Ораван, Маргетроид және С. Н. Журковтың қатты дененің қирау процесстеріне ұсынылған теорияларын қарастыру.
Лекция мәтіні (қысқаша)
Көп уақытқа дейін қатты денелердің беріктілік физикасының табиғатын олардың критикалық қирау түсінігімен қарастырып келгенін айтып өттік. Осы көзқараспен ақауы жоқ идеал дененің морт қирауын қарастырайық. Бұл денеге жүктелген жүк сол дененің теориялық беріктілігіне жеткенде, ол дене бірденінен атомдарға шашылып кеткен болар еді. Реал жағдайда денелер бірнеше бөлікке ғана бөлінетінін және жүктелген жүк шамасы теориялық беріктілікке жетпей қирайтыны белгілі (Гриффитс теориясы) . Бұл теорияның рас екендігін А. Ф. Иоффе өзінің экспериментінде дәлелдеген (NaCl кристалын су ертінді ортасындағы беріктілігі теориялық беріктілікке жақын болғаны байқалған) . Бірақ Гриффитс пен Иоффенің теориясы реал беріктілігінің шамасы теориялық беріктілік шамасынан төмен екендігін және денелер қирау барысында 2-3 бөлікке ғана бөлінетінін түсіндіргенімен, жүктелген жүктің әсер етуші уақыт мерзімі сол, жүктелген дененің беріктілік шамасына әсерін тигізуін түсіндіре алмайды. Мысалы, егер үлгі аз уақыт арасында жүктеліп, оның беріктілік шегі сол денеден жасалған үлгіні көп уақыт аралығында жүктелгендегі беріктілік шегіне қарағанда әлдеқайда жоғары екендігі байқалған. Бұл материалдың статикалық шаршауы деп аталады.
Денелердің статикалық шаршауын көптеген зерттеушілер силикат шыныларда, полимерлерде, металдарда, ионды кристалдарда т. б. материалдарда байқаған.
Материал беріктілігіне жүктеу уақытының әсерін, әр түрлі жылдамдықпен жүктегенде немесе деформациялағанда беріктіліктің шегі өзгеруінен, жылжығыштық тәсілі және ұзақ мерзімді беріктілігін анықтау барысында байқауға болады.
Уақыт мерзімінің дене беріктілігіне әсерін дененің критикалық қирау сипаттамасымен біріктіруге болмайды. Шынында да бір жағынан денеге жүктелген жүк белгілі шегіне жеткенде ғана қирайтын болса, екінші жағынан сол дененің беріктілік шегінің денені жүктеу мерзіміне (уақытына) тәуелділігі бір-біріне қайшы. Бұл қайшылыққа көптеген зерттеушілер көңіл аударғанымен, оны түсіндіру барысында статикалық көзқараста қалып қоя берген. Яғни, дене беріктілік проблемаларының шешімі болмаған. Мысалы, шыны материалдары беріктілігінің уақытқа тәуелділігін, Ораван Гриффитстің теориясын қолдана отырып, ауадан ылғалды сору арқасында беттік керілу коэффициентінің төмендеуімен түсіндірген:
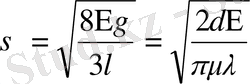
мұндағы Е - Юнг модулі, μ - Пуассон коэффициенті, λ - сызат ұзындығы, γ, δ - беттік керілу (δ <1)
Ораван теориясы бойынша, үлгі тез мерзімде жүктелсе, жаңа пайда болған сызат ылғалды сорып алуға үлгермейді, сызатта беттік керілу болмайды, сондықтан да беріктілік жоғары. Ал үлгі көп уақыт мерзімде жүктелген болса, жаңа сызат ылғалды сорып алуға үлгереді, беттік кернеу сына (клин) ретінде әсерін тигізіп беріктілік шамасын төмендетеді.
Маргетройд шыны беріктілігіне жүктеу мерзімінің әсерін, шыны екі фазадан тұруымен байланысты деп түсіндірген. Шыны гетерогенді жүйеден тұрады деп есептеп (квазитұтқырлы және серпінді элементтерден тұрады), уақыт мерзімі өткен сайын тұтқырлы пластиктив микробөлшектерде релаксация өтуі нәтижесінде серпінді элементінде кернеулік өсіп отырады. Бұл процесс серпінді элементіндегі кернеулік материалдың беріктілік шегіне жеткенше өседі де, материал қирайды, яғни материалдың беріктілігіне уақыт мерзімінің әсерін материалдың ішіндегі кернеуліктің таралу процесімен (релаксация) байланыстырылады. Бұл гипотезаны кейбір зерттеушілер, материал беріктілік шамасының уақыт мерзіміне тәуелділігін осы күнге дейін осылай түсіндіреді. Мысалы, поликристалды металдар үшін, әр түрлі физика-химиялық қасиеттері бар материалдарда олардың беріктілігіне уақыт мерзімі әсерін тигізетіндігі Ораванның теориясы орынсыз екендігін дәлелдейді. Мысалы, резина, пластмасса, фарфор, металдар, ионды кристалдар т. б. материалдар зерттелген. Олардың қирауына және беріктілігіне орта әр түрлі әсер ететіндігі бізге белгілі.
Сонымен, материалдың беріктілігі уақыт мерзіміне тәуелділігіне зерттеу жүргізу, ортаға байланысты емес екендігі анықталды. Оған қосымша дәлел, кейінгі кездегі вакуумда және инертті ортада жүргізген зерттеулер беріктіліктің уақыт мерзіміне тәуелділігін көрсетеді.
Ораван мен Маргетройдтың теориясы әр түрлі болғанымен, екі теория да әрбір материалдың беріктілік шегі барлығына қарсы емес. Яғни, беріктіліктің статикалық концепциясы сақталады, материалдың қирауы критикалық түрде өтеді деп есептеді. Беріктіліктің уақыт мерзіміне тәуелділігін сыртқы қосымша процестермен байланыстырады. Алдағы қарастырылатын феноменологиялық және жүктелген денедегі өтетін элементар процестерді зерттеу нәтижесінде дене беріктілігінің уақыт мерзіміне тәуелділігі сыртқы қосымша процестермен байланысты болмай, беріктіліктің уақытқа тәуелділігі - тікелей дененің қирау механизмімен байланысты екендігін дәлелдеді.
Сонымен, беріктіліктің уақытқа тәуелділігі, қатты денелердің қирау заңдылығы, жалпы физикалық табиғаты бар және сол табиғатпен тікелей байланыстылығын көрсетеді. Дене беріктілік проблемасына кинетикалық көзқараспен қарау, дене қирауы уақытқа байланысты дене ішінде қирау процесі жүріп, олардың жинақталуымен байланыстыру қажет. Олай болса, бұл процестерді анықтаудың ең оңай жолы - қатты денелердің жарамдылық мерзімін тұрақты температурада және тұрақты кернеуде анықтау. Яғни, дене жүктелген уақыттан бастап, сол дененің сол жүктің астында қирау үшін кеткен уақытты анықтау болып табылады. Материалдың механикалық беріктілігін анықтауда, кинетикалық қирау концепциясы бойынша материалдың жарамдылық мерзімі - фундаментальді шама болып есептеледі. Бұл шаманы қирау процесінде орташа қирау жылдамдығына кері пропорционал деп алуға болады:
 ∼
∼

Әрбір материалдың беріктілік қасиетін және олардың қирау табиғатын кинетикалық көзқараспен анықтау үшін, ол материалдың жарамдылық мерзімінің жүктелген кернеулікке және үлгіні сынау температурасына тәуелділігін анықтау қажет:
 (
(
 ) - ?
) - ?
Бақылау сұрақтары:
1. Беріктілік проблемасына статистикалық көзқарас. Гриффитс-Иоффе теориясы.
2. Беріктілік проблемасына кинетикалық көзқарас.
3. Ораванның теориясы.
4. Маргетроидтың теориясы.
5. Ораван теориясының дұрыс еместігіне дәлел.
3-лекция. Тақырыбы: Қатты денелердің жарамдылық мерзімі және беріктілік кинетикалық концепциясының негіздері.
Жоспары:
1. Жүктелген қатты денелердің жарамдылық мерзімін анықтау.
2. Жарамдылық мерзімнің кернеулікке тәуелділігі.
3. Одинг көзқарасы.
Лекция мақсаты Қатты дененің жарамдылық мерзімін анықтауға ұсынылған зерттеу тәсілі, жарамдылық мерзімнің кернеуге, температураға тәуелділігін қарастыру.
Лекция мәтіні (қысқаша)
Жүктелген қатты денелердің жарамдылық мерзімін, негізінде, үлгіні бір бағытта созу арқылы анықтаған. Ол үшін үлгіні пленкадан немесе фольгадан не болмаса топталған талшықтардан арнайы жасайды. Үлгі полимер пленка тәрізді болса, металл жұқа фольга тәрізді болса, арнайы пышақ арқылы жасалады:
Топталған талшық болса:
Ал кристалдардан талшық параллелепипед жасалып (арнайы пышақ арқылы) желімге отырғызылады.
Жасалған үлгілерді былай сынайды: белгілі температурада үлгіні, белгілі кернеулікпен жүктейді. Үлгі жүктелген кезден бастап, үлгі қирағанға дейінгі уақытты, яғни жарамдылық мерзімін анықтайды. Әр түрлі температурада және кернеулікте (80-90) үлгілердің жарамдылық мерзімі анықталады, бірақ бір үлгі үшін кернеу де, температурада тұрақты болуы қажет.
Арнайы қондырғы, үлгіні созу барысында оның деформациялануына қарамай, үлгі қирауына дейін жүктелген кернеуді тұрақты етіп ұстайды. Осы қондырғылардың арқасында жарамдылық мерзім 10 рет аралығында анықталған (10 -3 с - бірнеше ай аралығында) .
Жарамдылық мерзімнің температураға, жүктелген кернеулікке тәуелділігі көптеген материалдар үшін анықталған. Олар: поликристалды металдар - Санфирова, Бетехтин; әр түрлі монокристалдар - Бақтыбаев; металл емес қоспалар - Регель, Левин; полимерлер - Журков, Нарзуллаев, Аббасов; металды қоспалар - Бетехтин, Петров, Бақтыбаев; күрделі компазитты материалдар - Регель, Бетехтин, Бақтыбаев; цемент тастар, бетондар - Бақтыбаев, Кадырбеков.
Барлық зерттелген материалдар үшін температура тұрақты болған кезде, жарамдылық мерзімнің кернеулікке тәуелділігін былай жазуға болады:
 =
=
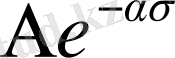 (1)
(1)
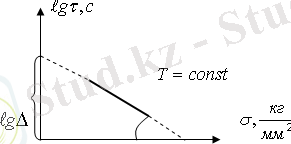 А, α - осы материалдың тұрақты шамасы.
А, α - осы материалдың тұрақты шамасы.
Жарамдылық мерзім ортаға байланысты емес екенін дәлелдеу үшін, зерттеуді вакуумда не болмаса инертті ортада жүргізген. Бұл формуланы
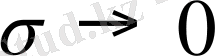 болған кезде қолдануға болмайды, себебі сызықты lg
болған кезде қолдануға болмайды, себебі сызықты lg
 - σ тәуелділік орындалмайды. Оның себептерін кейін қарастырамыз.
- σ тәуелділік орындалмайды. Оның себептерін кейін қарастырамыз.
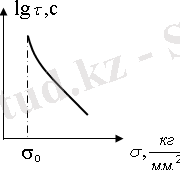 Кейбір зерттеушілер, мысалы, И. А. Одинг және басқалар lg
Кейбір зерттеушілер, мысалы, И. А. Одинг және басқалар lg
 - σ қисығы асимтотикалық ординатаға жетпей, ординатаға параллель оське жақындайды, σ
о
қауіпсіздік кернеу деп есептеген. Бұл көзқарасты тексеру өте қиын,
- σ қисығы асимтотикалық ординатаға жетпей, ординатаға параллель оське жақындайды, σ
о
қауіпсіздік кернеу деп есептеген. Бұл көзқарасты тексеру өте қиын,
өйткені σ
о
кездегі жарамдылық мерзімі
 өте үлкен шама. Бұл көзқарас
өте үлкен шама. Бұл көзқарас
теорияға қарсы болмағанымен дискуссиялық көзқарасқа жатады. Сол үшін біз қазірше тек lg
 - σ тәуелділіктің тура сызықты жағын қарастырамыз. Барлық зерттелген материалдарға бұл теңдеудің орындалуы, жарамдылық мерзім жүктелген денеде өтетін қирау процесінің жинақталуына кетеді деп есептеуге болады. Бұған дәлел, үлгіні жүктеуді бірнеше рет тоқтатып, қайтадан сол шамаға жүктеген кездегі қирауға кеткен жарамдылық мерзім, тоқтаусыз үзбей жүктеген кездегі жарамдылық мерзімге қарағанда аз болғаны дәлел бола алады.
- σ тәуелділіктің тура сызықты жағын қарастырамыз. Барлық зерттелген материалдарға бұл теңдеудің орындалуы, жарамдылық мерзім жүктелген денеде өтетін қирау процесінің жинақталуына кетеді деп есептеуге болады. Бұған дәлел, үлгіні жүктеуді бірнеше рет тоқтатып, қайтадан сол шамаға жүктеген кездегі қирауға кеткен жарамдылық мерзім, тоқтаусыз үзбей жүктеген кездегі жарамдылық мерзімге қарағанда аз болғаны дәлел бола алады.
Енді жүктелген денедегі өтетін процестер, сол дененің қирауына алып келетін болса, сол процестің табиғатын анықтау мақсатында жарамдылық мерзім шамасына температураның әсерін анықтау қажет. Сонымен, lg
 - σ тәуелділігін әр түрлі температурада анықталған. Әр температураның lg
- σ тәуелділігін әр түрлі температурада анықталған. Әр температураның lg
 - σ тәуелділігі тура сызықты, температура өскен сайын lg
- σ тәуелділігі тура сызықты, температура өскен сайын lg
 - σ қисығы енкіштігі ұлғайып, температура төмендеген сайын lg
- σ қисығы енкіштігі ұлғайып, температура төмендеген сайын lg
 - σ сызығы тік сызыққа жақындайтыны байқалған. Бұны график түрінде былай көрсетуге болады:
- σ сызығы тік сызыққа жақындайтыны байқалған. Бұны график түрінде былай көрсетуге болады:
Белгілі бір жарамдылық мерзім шамасында барлық lg
 - σ сызықтар
- σ сызықтар
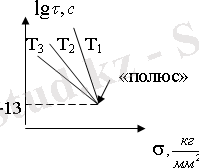 бір нүктеге қосылатындығы байқалған. Ол жарамдылық мерзім ∼10
-13
с тең. Сызықтардың қосылатын нүктесін «полюс» деп атаған. График түрде былай көрсетуге болады:
бір нүктеге қосылатындығы байқалған. Ол жарамдылық мерзім ∼10
-13
с тең. Сызықтардың қосылатын нүктесін «полюс» деп атаған. График түрде былай көрсетуге болады:
Жарамдылық мерзімнің «полюстағы» шамасы τ ≈ 10
-12
÷ 10
-13
с, lg
 = -13.
= -13.
Жарамдылық мерзімнің Т, σ тәуелділігін аналитик түрде былай жазуға болады:
τ = τ

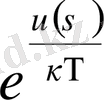
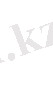 (2),
(2),
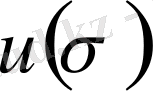 =
=
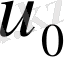 -
-

γ және
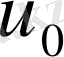 - тұрақты шамалар, олардың физикалық мәнін кейін қарастырамыз.
- тұрақты шамалар, олардың физикалық мәнін кейін қарастырамыз.
Екінші формуланың экспериментті нәтижелерді тура түсіндіретінін тексеру үшін, бұл формуланы былай жазуға болады:
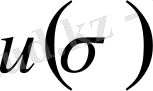 =
=
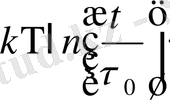 (3)
(3)
Бұл формулаға қарағанда барлық тура сызықтар бір сызыққа:
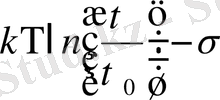 жинақталуы қажет. Дененің қирау табиғатын (2) -формуланы талдау арқылы анықтауға болады. Бұл формула жарамдылық мерзімнің негізгі теңдеуі болып есептеледі.
жинақталуы қажет. Дененің қирау табиғатын (2) -формуланы талдау арқылы анықтауға болады. Бұл формула жарамдылық мерзімнің негізгі теңдеуі болып есептеледі.
Бақылау сұрақтары:
- Дене қирау табиғаты кинетикалық көзқараспен өтуін анықтау.
- Жарамдылық мерзімі және кинетикалық концепциясының негіздері.
- И. А. Одинг және басқалардың көзқарасы.
- Жарамдылық мерзімнің механикалық кернеуге тәуелділігі.
- Жарамдылық мерзімнің температураға тәуелділігі.
4-7 лекция. Тақырыбы: Жарамдылық мерзімді анықтау тәсілі.
Жоспары:
1. Материалдың жарамдылық мерзімін бір бағытта үлгіні тарту арқылы анықтау.
2. Үлгіні қысқа уақыт аралығында жүктеу тәсілі.
3. Материалдың беріктілігіне ортаның әсер етуі.
Лекция мақсаты: Жарамдылық мерзімді жылжығыштық анықтайтын тәсілдердің жұмыс атқаруымен таныстыру.
Лекция мәтіні (қысқаша) :
Жоғарыда айтылғандай материалдың жарамдылық мерзімін бір бағытта үлгіні тарту (созу) арқылы анықталады. Ол үшін үлгі біртекті деформацияланып, көлемі өзгермейтін жағдайда үлгінің көлденең кесімі деформацияның арқасында былай азаяды:
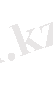 S =
S =
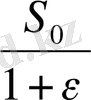 ,
,
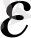 =
=
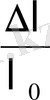
Олай болса, үлгіге әсер етуші кернеу өсуі
 =
=
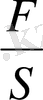 =
=
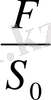 (1+ε) болады. Үлгіге әсер етуші кернеу тұрақты болу үшін, жүктелген күш деформация барысында былай кемуі керек:
(1+ε) болады. Үлгіге әсер етуші кернеу тұрақты болу үшін, жүктелген күш деформация барысында былай кемуі керек:
F(ε) =
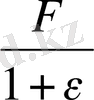 , F = P
, F = P
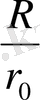
 = const болу үшін ілінген Р жүктің иығы
= const болу үшін ілінген Р жүктің иығы
 =
=
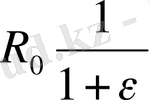 шамаға өзгеріп тұруы керек. R-дің деформация барысында мұндай өзгеруін Э. Е. Томашевский және А. И. Слуцкер есептеп тапқан рычаг фигурасының профилі, полярлық координат бойынша былай болу қажет:
шамаға өзгеріп тұруы керек. R-дің деформация барысында мұндай өзгеруін Э. Е. Томашевский және А. И. Слуцкер есептеп тапқан рычаг фигурасының профилі, полярлық координат бойынша былай болу қажет:
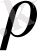 =
=
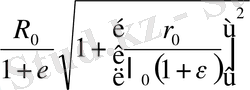
 - үлгінің бастапқы ұзындығы.
- үлгінің бастапқы ұзындығы.
Рычагтың (1-сурет) негізгі параметрі
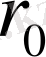 сыналатын материалдың қасиетіне байланысты. Егер материалдың деформациясы көп болмаса, (ε<<1)
сыналатын материалдың қасиетіне байланысты. Егер материалдың деформациясы көп болмаса, (ε<<1)
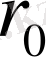 радиусты үлгі ұзындығы
радиусты үлгі ұзындығы
 тең етіп алуға болады. Егер деформация ε ≈2÷3 болса,
тең етіп алуға болады. Егер деформация ε ≈2÷3 болса,
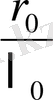 = 2
= 2
 .
.
Практикада рычагты деформация барысында 270
 бұрышқа бұру мүмкін. Рычагты дайындау дәлдігін асыру мақсатында рычаг өлшемдері үлкен болуы қажет. Сол себепті
бұрышқа бұру мүмкін. Рычагты дайындау дәлдігін асыру мақсатында рычаг өлшемдері үлкен болуы қажет. Сол себепті
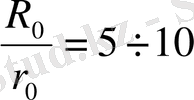 аралығында болады.
аралығында болады.
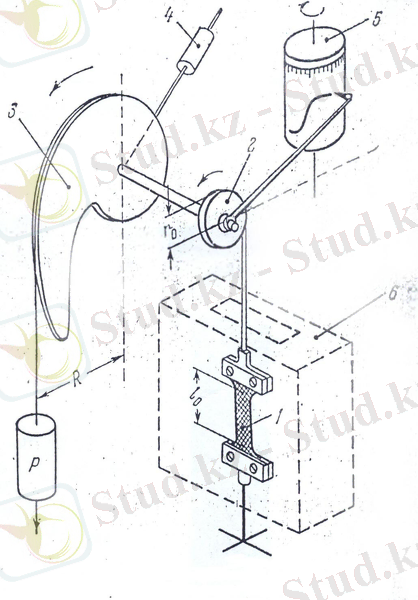
1-cурет. Жарамдылық мерзімді анықтайтын қондырғының схемасы. 1-үлгі, 2-блокпен иілгіш, 3-фигуралы рычаг, 4-фигуралы рычагты теңестіретін ауырлық, 5-ішінде сағат механизмі бар барабан, жылу излояцияланбайтын камера.
Бұл қондырғы арқылы жарамдылық мерзімді бірнеше секундтан, бірнеше ай аралығында анықтауға болады. Жарамдылық мерзімді анықтауда төменгі жағынан шектеулі қондырғының конструкциясына байланысты, үлгіні жүктеуге кететін уақыт 2-3 секундты талап етеді. Ал жарамдылық мерзімнің σ, Т-ға тәуелділігін дәл анықтау үшін, жарамдылық мерзімді өлшейтін интервал үлкен болуы қажет. Бірақ интервалды үлкейту, яғни айдан жылға өту перспективасыз, себебі өлшеу интервалы бір реттікке ғана өседі. Ал қысқа жарамдылық мерзімді анықтау, мысалы,
 с жарамдылық мерзім интервалын 3-4 ретке кеңітеді. Сонымен қатар, материалдардың соққы (удар) жүктелуінде қирауы практикада көп кездескен себепті, бұл бағытта қирау барысын зерттеу қажет болатындығы белгілі.
с жарамдылық мерзім интервалын 3-4 ретке кеңітеді. Сонымен қатар, материалдардың соққы (удар) жүктелуінде қирауы практикада көп кездескен себепті, бұл бағытта қирау барысын зерттеу қажет болатындығы белгілі.
Сонымен, үлгіні қысқа уақыт аралығында жүктеу тәсілін табу қажет. Ол үшін кіші интервалды өлшейтін жүйе табу керек. Тез өтетін механикалық процестерді зерттеуге инерциясыз электр өлшеу тәсілдері қолданылады. Бұл электр тәсілінің негізгі элементі болып, электр сигналын беретін көрсеткіштер (датчиктер) жатады. Көрсеткіштер арқылы механикалық шамалар анықталады. Көрсеткіштердің түрлері көп (А. М. Туричин, «Электрические измерения не электрических величин») . Көрсеткіштен пайда болған сигналдар күшейтіріліп, катод не болмаса шлейфті осциллограф арқылы тіркеледі. Аз шамадағы жарамдылық мерзімді өлшейтін қондырғыны электродинамикалық тартып қирату машинасы деп атайды. Бұл машина бірінші рет Санкт-Петербург қаласындағы физика-техникалық институттың, беріктілік физикасы зертханасында С. Н. Журков басшылығымен Э. Е. Томашевский құрастырған (2-сурет) .
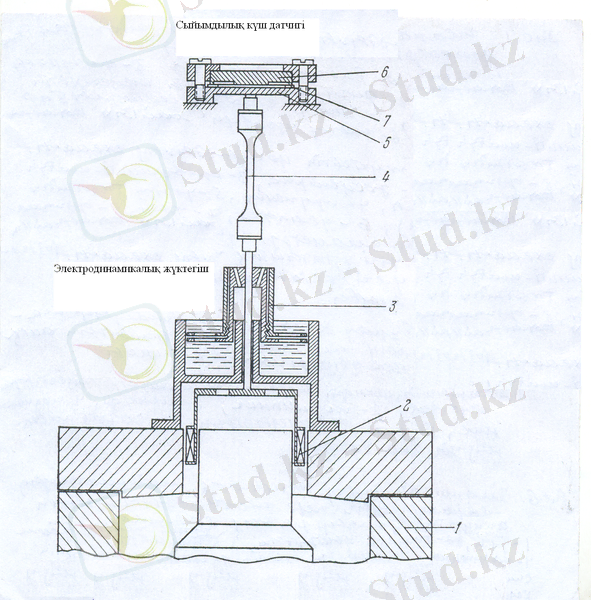
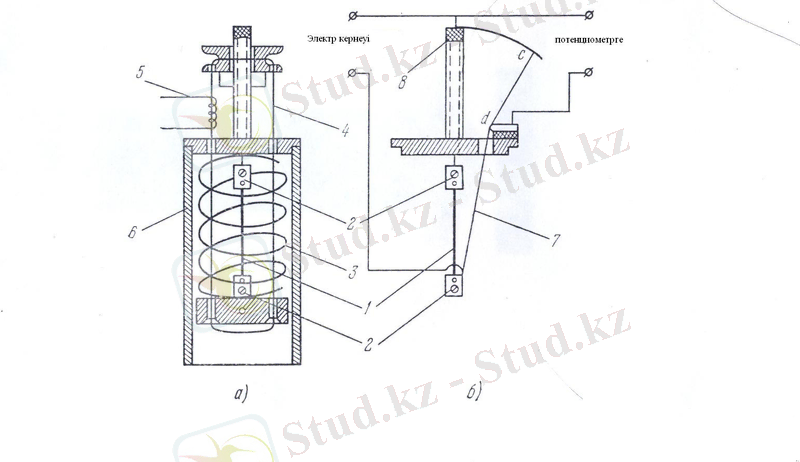
2-сурет. Кіші мөлшердегі жарамдылық мерзімді өлшейтін қондырғының схемасы. 1-саңлауы бар магнит, 2-үлгімен қосылған катушка, 3-сұйықтық демпфер, 4-үлгі, 5-күш датчигінің мембранасы, 6-датчиктің екінші электроды, 7-мембрана мен конденсатордың арасына қойылған смодадан жасалған сақина.
Бұл қондырғының негізін сыйымдылық күш көрсеткіші және сұйық демпферлі электродинамикалық жүктегіш құрайды. Үлгіні жылдам жүктеу электродинамикалық қондырғы арқылы жүргізіледі. Электродинамикалық қондырғы сақина тәрізді саңылауы бар магниттен(1) тұрады. Сақина тәрізді саңылауға сынайтын үлгімен қосылған катушка орналасқан. Саңылауда магнит өрісі магниттелген коэрцитивті қоспа арқылы не болмаса магниттеуші катушка(2) арқылы жасалады. Қозғалатын катушкадан электр тогы өткенде, мынаған тең Ампер күші пайда болады:
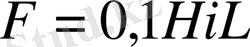
мұндағы: Н-магнит өрісінің кернеулігі, i-катушкадан өтетін ток, L-катушканың ұзындығы.
Бұл күш үлгіні жүктеуге қолданылады. Катушканың қозғалу үдеуі, ауырлық үдеуінен 100 есе үлкен болуы мүмкін. Үлгі мен катушка аралығында сұйықтық демпфер(3) орналастырылады. Ол арқылы әсер ететін күш импульсінің формасын (3-сурет) өзгертуге болады.
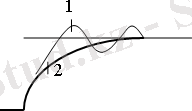 3-сурет. Үлгіні бір бағытта тарту күші өсуінің осциллограммасы. 1-демпфер жоқ кездегі кернеудің өзгеруі, 2-демпфер қосылған кездегі кернеудің өзгеруі.
3-сурет. Үлгіні бір бағытта тарту күші өсуінің осциллограммасы. 1-демпфер жоқ кездегі кернеудің өзгеруі, 2-демпфер қосылған кездегі кернеудің өзгеруі.
Демпфер үлгіні жүктеу диаграммасын өзгертеді екен. Демпфер арқылы үлгіні тербеліс режим жүктеуден апериодикалық жүктеуге болады. 2-ші сызықтың формасын демпфердің үйкеліс коэффициентін өзгерту арқылы жасауға болады. Үлгіге әсер етуші күштің өсуі 2*10 -3 ÷ 10 -2 с аралығында жатады. Жүктеу уақытының шектелуі қолданған тәсілдің мүмкіншілігінде емес, ол зерттелетін материалдың қасиетіне және серпінді импульстің үлгі бойымен таралу жылдамдығына байланысты, яғни табиғатты шектелу болып есептеледі. Жүктеу уақытын қысқарту үшін, тек үлгінің ұзындығын қысқарту арқылы болады.
Сонымен бұл қондырғы жоғары жиілікті сыйымдылықты күш күшейткіштен, жоғары жиілікті лампалы генератордан, детекторлайтын схемадан және катодты осциллографтан тұрады. Бұл электродинамикалық машинаны созылу деформациясы аз материалдардың жарамдылық мерзімін анықтауға (2*10 -3 ÷ 10 -2 с) болады. Пластикалық деформациясы жоғары материалдарға қолдану үшін электродинамикалық жүктейтін бөлшек, жүктелген кернеулік шамасын автоматты түрде деформация барысында тұрақты етіп ұстап тұруы қажет (σ = const) . Ол үшін саңылауда қозғалатын катушка біртексіз арнайы орамнан жасалуы қажет не болмаса саңылауда арнайы біртексіз магнит өрісін жасау қажет. Бүгінгі таңда ондай қондырғы тәсілін ешкім жасамаған. Материал беріктілігіне ортаның әсерін анықтау үшін, басқаша айтқанда Ораванның теориясын тексеру үшін Журков, Левин, Томашевский бірінші рет вакуумда және инертті ортада зерттеу жүргізді. Олардың зерттеуі бойынша, беріктіліктің уақытқа тәуелділігі тек ортаға тәуелді еместігін дәлелдейді. Вакуум жасайтын жүйе форвакуум сорғыштан (насос) - ВН-461 және май булы сорғыштан (парамаслянный) - ЦВЛ-100 тұрады. Қалған бөлшектері материалды жүктеу және кернеулікті тұрақты ұстайтын бөлшектер.
Күрделі жағдайда материалдардың жарамдылық мерзімін анықтау тәсілдері.
Біз материалдарды бір бағытта тарту тәсілімен жарамдылық мерзімін қалай анықталатынын қарастырдық. . Бұл қарапайым тәсілден басқа, материалдарды күрделі жағдайда сынау зерттеулері де жүргізілген. Күрделі сынауға материалдарды циклды жүктеу, бұрау, бұрап тарту, гидростатикалық қысым ортасында, радияцияның әсері, әр түрлі сұйық орталарда зерттеулер жатады. Біз бұл тәсілдерге қысқаша тоқталып өтеміз, себебі, әрбір тәсілдің практикада өзінің орны бар. Бірақ материалдардың қирау процесін физика негізінде анықтауға аса айтарлықтай үлес қоспайды. Сонымен материалдардың шаршау тәсіліндегі жарамдылық мерзімі қалай анықталатынына тоқталамыз.
Валға отырғызылған эксентристі моторға қосып, кривошип-шатун механизмі серіппені (пружина) тартып, демпфер арқылы үлгіге және динамометрге жүк түсіреді (4-сурет) .
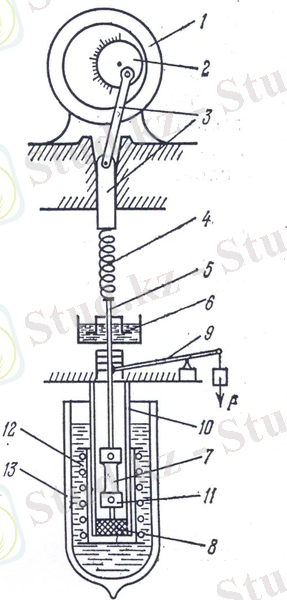
4-сурет. Үлгіні циклді жүктейтін қондырғының схемасы. 1-мотор, 2-эксцентрик, 3-кривошипті шатун механизмі, 4-пружина, 5-үлгіні тартатын сым (тяга), 6-демпфер, 7-үлгі, 8-динамометр, 9-динамометрді градуировка жасайтын рычаг, 10-үлгі ұстағыштың трубкасы, 11-қозғалмайтын үлгі ұстағыш, 12-қыздырғыш, 13-Дьюар ыдысы.
Үлгіге түсірілген жүк уақыт барысында мынадай заңдылықпен өзгереді:
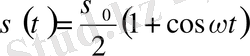
мұндағы,
 - жүктелген кернеудің амплитуда шамасы;
- жүктелген кернеудің амплитуда шамасы;
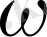 - айналмалы жиілік (циклді) .
- айналмалы жиілік (циклді) .
Уақыт барысында
 = const болу үшін, алынған серіппе мынадай шартқа сай болуы керек:
= const болу үшін, алынған серіппе мынадай шартқа сай болуы керек:
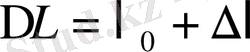
 - серіппе бастапқы деформациясының амплитудалық шамасы;
- серіппе бастапқы деформациясының амплитудалық шамасы;
 - үлгінің бастапқы ұзындығы;
- үлгінің бастапқы ұзындығы;
 - қирау алдындағы үлгінің деформация шамасы (
- қирау алдындағы үлгінің деформация шамасы (
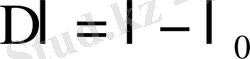 ) .
) .
Егер үлгінің көлемі деформация барысында өзгермесе және үлгіде мойын (шейка) пайда болмаса, үлгінің қирау алдындағы кернеулігі:
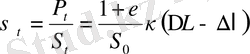
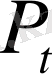 - қирау алдындағы жүктелген жүк;
- қирау алдындағы жүктелген жүк;
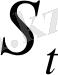 - қирау алдындағы үлгінің көлденең ауданы;
- қирау алдындағы үлгінің көлденең ауданы;
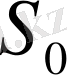 - үлгінің бастапқы көлденең ауданы;
- үлгінің бастапқы көлденең ауданы;
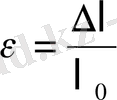 - қирау алдындағы үлгінің салыстырмалы ұзаруы;
- қирау алдындағы үлгінің салыстырмалы ұзаруы;
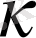 - серіппенің қаттылық шамасы.
- серіппенің қаттылық шамасы.
Үлгінің қирау алдындағы кернеулігін былай жазуға болады:
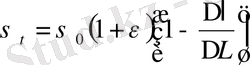
Олай болса, сынау барысында үлгідегі кернеулік тұрақты болу үшін:
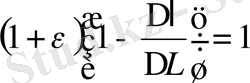 болуы керек, шынында да
болуы керек, шынында да
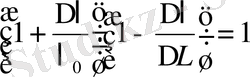 . Бұдан
. Бұдан
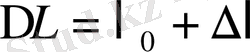 келіп шығады. Бұл серіппеге қойылатын шарт болатын (жоғарыда айтып кеткенбіз) . Бұл тәсілді бірінші рет Регель, Лексовский жасаған.
келіп шығады. Бұл серіппеге қойылатын шарт болатын (жоғарыда айтып кеткенбіз) . Бұл тәсілді бірінші рет Регель, Лексовский жасаған.
Енді материалдарды бұрау кездегі жылжығыштықтың жарамдылық
мерзімін анықтауын қарастырайық.
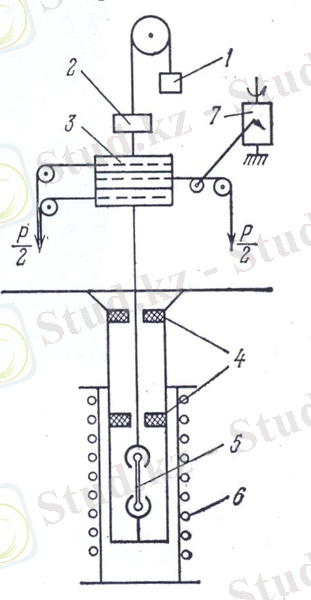
5-сурет. Үлгіні бұрау кезіндегі материалдың жарамдылық және жылжығыштығын анықтайтын қондырғының схемасы. 1-тартқышты, шкифті және подшипникті (2) теңестіруші ауырлық, 2-подшипник, 3-шкиф, 4-подшипник, 5-үлгі, 6-қыздырғыш, 7-сағат механизмі бар барабан.
Бұрау кездегі дененің жылжығыштығын және қирауын, денені бұрайтын екі күш шкив арқылы үлгіге әсер етеді (5-сурет) . Шкив үлгімен біртұтас бекітіледі. Бұрау барысында үлгінің өлшемі өзгермейтін себепті, үлгіде тұрақты кернеу болу үшін, бұрайтын күш моментінің тұрақты болуы жеткілікті. Бұл тәсілді бірінші рет В. А. Степановтың басшылығымен Шпейзман құрастырып зерттеу жүргізген (Санкт-Петербург, физика-техникалық институт, В. А. Степановтың зертханасында) .
6-сурет. Гидростаттикалық қысымда материалдардың жарамдылығын және жылжығыштығын анықтайтын қондырғының схемасы. 1-үлгі, 2-төменгі қыстырғыш, 3-үлгіні жүктейтін спиральді пружина, 4-кпроннан жасалған жіп, 5-капронды күйдіретін спираль, 6-металдан жасалған обойма, 7-үлкен кедергілі нихромнан жасалған сым.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz