Алгоритмдер теориясы. Анықтамасы. Қасиеттері. Түрлері. Алгоритмді жазу әдістері. Алгоритм модельдері

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 34 бет
Таңдаулыға:

2-БӨЛІМ. ДӘРІС КЕШЕНІ

1-БӨЛІМ. АЛГОРИТМДЕР ТЕОРИЯСЫНА КІРІСПЕ

Глоссарий

Алгоритмдер теориясы - алгоритмдердің жалпы қасиеттері мен заңдылықтарын, олардың ұғымдарының формальды модельдерін оқытатын ғылым

Алгоpитм - кез келген алғашқы мәліметтен ( берілген алгоритм үшін мүмкін алғашқы мәліметтердің қандай да бір жиынтығынан) басталатын және осы алғашқы мәліметпен толық анықталатын нәтиже алуға бағытталған алгортмдік үрдісті беретін дәл нұсқаулар тізбегі

Алгоритмдік үрдіс - конструктивті объектілерді (сөз, сан, сөз жұбы, сан жұбы, сөйлемдер және т. б. ) дискретті қадаммен түрлендіру үрдісі.

Алгоритмнің негізгі қасиеттері : дискреттілік, түсініктілік, анықтылық, нәтижелік, көпшілік.

Алгоритмді орындаушы - бұл алгоритммен тағайындалатын әрекеттерді орындай алатын абстрактілі немесе нақты жүйе (техникалық, биологиялық немесе биотехникалық) .

Тьюринг машинасы - белгілі бір есептерді шығаруға арналған қатаң математикалық құрылым, математикалық аппарат

Сөз - әлдебір алфавиттен алынған әріптердің кез келген тізбегі

Сөз ұзындығы - с өздегі әріптердің саны

Енгізілетін сөз - алгоритмде қолданылатын сөз

Шығарылатын сөз - алгоритмнің нәтижесі

Пост алгоритмдік машинасы - абстрактылы машина, бірнеше бірдей секцияларға бөлінген, оқу-жазу инесі бар шексіз лентадан тұрады.

Есептелетін функция - ә лдебір алгоритм көмегімен есептелетін функция

Іс жүзінде алгоритм - функцияны беру әдісі

Черч тезисі алгоритмдік - есептелетін бөлшекті сандық функциялар класы барлық бөлшекті рекурсивті функциялар класымен беттеседі.

Бөлшекті рекурсивті функция - есептелетін бөлшекті функция интуитивті ұғымының ғылымы эквиваленті бола алады.

1-дәріс: Алгоритмдер теориясы. Анықтамасы. Қасиеттері. Түрлері. Алгоритмді жазу әдістері. Алгоритм модельдері.

Дәріс мақсаты: Алгоритмдер теориясының анықтамаларын қарастыру, оның шығу тарихына шолу жасау, алгоритмдер модельдерін қарастыру.

Алгоритмдер теориясының негізгі анықтамалары
Алгоритмдер теориясының шығу тарихы
Алгоритмдер теориясының мақсаты мен міндеті.
Алгоритмдер теориясының нәтижелерін практикалық қолдану

Алгоритмдер теориясы - алгоритмдердің жалпы қасиеттері мен заңдылықтарын, олардың ұғымдарының формальды модельдерін оқытатын ғылым. Алгоритмдерді формализациялау негізінде олардың тиімділігі бойынша салыстыру, эквиваленттілікті тексеру, қолданылу облысын анықтау мүмкіндіктері бар.

1930 жылдары құрастырылған алгоритмдердің формальды модельдері (Пост, Тьюринг, Черч) 1950-жылдардағы Колмогоров және Марковтың модельдерімен тең, себебі бір модельде шешілетін кез келген проблемалар класы басқа да модельмен шешіледі. Қазіргі кезде алгоритмдер теориясы негізінде практикалық ұсыныстарды көптеген жобалау және программалық жүйелерді құрастыру облыстарында көруге болады.

Ең алғашқы интуитивті түсінікте бізге жеткен алгоритм - қойылған есепті шешетін ақырлы элементарлы тізбектелген әрекеттер, біздің эрамызға дейінгі 3-ғасырдағы Евклид ұсынған екі санның ең үлкен ортақ бөлгішін табу болды. Оны Евклид алгоритмі деп атады. 20-ғасырға дейін ұзақ уақыт бойы алгоритм сөзі Евклидтік алгоритм сөзімен тұрақты тіркесіп айтылатын. Басқа математикалық есептерді қадамдап шешуді сипаттау үшін «әдіс» сөзі қолданылды. Бастапқы алгоритмдер теориясының заманауи жұмысын неміс математигі Курт Гёдель (1931 жылы) жазды. Ол символикалық логиканың толықсыздығы туралы теорема жазды. Онда бірқатар математикалық проблемалардың әлдебір класқа жататын алгоритмдермен шешілмейтіндігі көрсетілді. 1936 жылы тәуелсіз түрде Алан Тьюрингтің, Алоиз Черчтің, Эмиль Посттың фундаментальды жұмыстары жасалды. Тьюринг машинасы, Пост машинасы және Черчтің лямбда-санақ машиналары пайда болды. Олар өздері ұсынған формальды жүйелермен алгоритмнің интуитивті ұғымдарын эквивалентті деп есептеді. Оның негізінде алгоритмдік тұрғыдан шешілмейтін проблема болмайтындығы дәлелденді.

1950-жылдары Колмогоров және Марков алгоритмдер теориясына көп үлес қосты. 1960-70-жылдары келесі бағыттар пайда болды:

Алгоритмдердің классикалық теориясы (формальды тілдер терминдеріндегі есептің қойылымы, шешілетін есептер ұғымы, күрделі кластарды енгізу, 1965 жылы Эдмондс ашқан P=NP проблемалары, NP- толық есептер класының ашылуы және оның зерттелуі) ;
Алгоритмдердің асимптотикалық анализі (алгоритмдердің күрделілігі және көлемділігі, алгоритмдерді бағалау шарты, рекурсивті алгоритмдерді асимптотикалық бағалау әдістері), Кнут, Ахо, Хопкрофт, Ульман, Карп жұмыстарында көрсетілді;
Есептеуіш алгоритмдердің практикалық анализін (айқын көлемді еңбек функциясының алынуы, функцияның аралық анализі, алгоритмнің практикалық сапасын бағалау, рационалды алгоритмдерді таңдау әдістемесі) Д. Кнут «ЭЕМ үшін программалау өнері» жұмысында көрсетті.

Алгоритмдер теориясының мақсаты мен міндеті. «алгоритм» ұғымын формальдандыру және формальды алгоритмдік жүйелерді зерттеу; Бірқатар есептердің формальды түде алгоритмдік шешілмейтіндігін дәлелдеу; Есептердің классификациясы, күрделі кластарды анықтау және зерттеу; Алгоритмдер күрделілігін асимптотикалық анализдеу; Рекурсивті алгоритмдерді анализдеу және зерттеу; Алгоритмдерді салыстырып анализдеу мақсатында айқын көлемді еңбек функциясын алу; Алгоритмдердің сапасын салыстырмалы түрде бағалау шарттарын құрастыру.
Алгоритмдер теориясының нәтижелерін практикалық қолдану

Екі аспектіде қолданылады:

Теориялық аспект : қандай да бір есепті зерттеу кезінде алгоритмдер теориясының нәтижесі мына сұраққа жауап береді - бұл есеп алгоритмдік тұрғыдан шешілетін есеп пе, егер шешілетін есеп болса, бұл есептің NP- толық есептер класына жататындығын зерттеу. Егер оған жатса, онда үлкен көлемді бастапқы берілгендер үшін дәл шешім алуға көп уақыт шығынын есептеу керек.

Практикалық аспект : алгоритмдер теориясының әдістері мен әдістемелері (асимптотикалық және практикалық анализ) келесі сұрақтарды қарастырады:

Берілген есепті шешуге арналған алгоритмдер жиынынан есепті қолдану ерекшелігін ескере отырып рационалдысын таңдау (бастапқы берілгендердің көлеміне шектеу қойылса, қосымша жадының көлеміне шектеу қойылса) ;
Күрделі есептерді шешудің уақыттық бағалауын алу;
Криптографиялық әдістер үшін маңызды болып саналатын әлдебір есептің белгілі бір уақыт аралығында шешілмейтіндігі туралы шынайы бағалау алу;
Есепті шешу тиімді алгоритмдерін практикалық анализ негізінде ақпарат өңдеу облысында құрастыру және жетілдіру.

Алгоритм ұғымын формальдандыру

Алгоритм ұғымы информатиканың ақпарат сияқты негізгі ұғымдарының бірі болып табылады.

Анықтама 1. 1.

Бұл - алгоритм ұғымының интуитивті сипатталуы болып табылады. Алгоритмдік үрдіс - конструктивті объектілерді (сөз, сан, сөз жұбы, сан жұбы, сөйлемдер және т. б. ) дискретті қадаммен түрлендіру үрдісі.

Алгоритмнің негізгі қасиеттері : дискреттілік, түсініктілік, анықтылық, нәтижелік, көпшілік.

Орындаушыны - орта, элементарлық әрекеттер, командалар жүйесі, әрекеттерінің «формальдығы» сипаттайды . Информатикада әмбебап алгоритм орындаушысы компьютер болып табылады.

Орындаушының командалар жүйесі - орындаушы орындай алатын барлық командалар жиынтығы. Әрбір команда үшін қолдану шарттары берілуі (ортаның қандай жағдайында команда орындалуы мүмкін) және команданың орындалу нәтижелері жазылған болуы тиіс. Команданы шақырғаннан кейін орындаушы сәйкес элементарлық әрекеттерді орындайды.

Орындаушы «формальды» түрде әрекет етеді, яғни есептің мазмұнына үңілмейді, тек қана қажетті нәтиже алу үшін қатаң түрде әрекеттерді (командаларды) орындайды. Енді алгоритм орындаушысы ұғымын қолдана отырып алгоритм ұғымын анықтауға болады.

Алгоpитм - алдыға қойылған есептің шешіміне ақырлы қадаммен жету үшін қажетті қимылдар тізбегінің орындаушыға түсінікті және дәл нұсқаулары.

Алгоритм іргелі ғылыми ұғым ретінде қатаң сипаттауды талап етеді, яғни «формальдауды». Алгоритм ұғымы формальдаудың келесі бағыттары белгілі:

шекті және шексіз автоматтар теориясы (Пост, Тьюринг машиналары, Марковтың қалыпты алгоритмдері және т. б. ) ;
есептелетін (рекурсивті) функциялар теориясы;
Черчтің λ-есептеуі (LISP бағдарламалау тілі) .

Алгоритм ұғымын формальдаудың негізгі мақсаты: әртүрлі математикалық есептердің алгоритмдік шешілу мәселелерін қарастыру, яғни есептің шешілуіне әкеп соғатын алгоритм тұрғызуға бола ма деген сұраққа жауап беру.

D - есептің бастапқы берілгендерінің облысы (жиыны) болсын. R - мүмкін нәтижелер жиыны болсын, онда алгоритм D --> R бейнелеуін орындайды. Бұл бейнелеу толық емес болғандықтан, келесі ұғымдар қажет:

Алгоритм бөлікті алгоритм деп аталады, егер D облысынан алынған d үшін ғана нәтиже алатын болсақ. Егер частичным алгоритмом, если мы получаем результат только для некоторых d из D D облысынан алынған барлық d үшін дұрыс нәтиже алынса, онда толық алгоритм деп аталады.

Алгоритмнің формальды анықтамалары өте көп. Олардың барлығының дәлелдемелері бар.

Анықтама 1. 2 (Колмогоров) : Алгоритм - қандай да бір қадамдар санынан кейін қойылған есептің шешіміне әкелетін, қатаң анықталған ережелерге сәйкес орындалатын, кез келген есептеу жүйесі

Анықтама 1. 3 (Марков) : Алгоритм - өзгеретін бастапқы берілгендерден нәтижелерге қарай жүретін есептеу процесін анықтайтын дәл сипаттама.

Өзін-өзі бақылау сұрақтары:

Алгоритмдер теориясының негізін қалаушы кім?
Алгоритмдер теориясының интуитивтілігі неде?
Колмогоровтың алгоритмдерге берген анықтамасы?
Марковтың алгоритмдерге берген анықтамасы?
Бөлікті алгоритм деген не?
Алгоритмнің негізгі қасиеттері
Алгоритм ұғымын формальдандыру
Алгоритмнің теориялық аспектісі
Алгоритмнің практикалық аспектісі
Алгоритмдер теориясының мақсаты мен міндеті.

2-дәріс: Алгоритм ұғымын тереңдету, анықтау. Тьюринг машинасын программалау. Пост алгоритмдік машинасы алгоритм ұғымын дәлелдеуші.

Дәріс мақсаты: Тьюринг, Пост машиналарына түсініктеме беру. Алгоритмдердің ұғымын тереңдету.

Алгоритм ұғымын тереңдету анықтамалары
Тьюринг машинасы
Пост алгоритмдік машинасы
Марков алгоритмдік машинасы

Алгоритм абстрактілі машина іспеттес.

Тьюринг машинасы - белгілі бір есептерді шығаруға арналған қатаң математикалық құрылым, математикалық аппарат. Бұл аппарат машина деп аталу себебі оның құрамдас бөлігінің және функцияларының есептеу техникасына ұқсауында. Тьюринг машинасының есептеу техникасынан ерекшелігі оның еске сақтау құрылғысы шексіз лентадан тұруында, ал есептеу техникасының еске сақтау құрылғысы қаншалықты үлкен көлемді болса да шектеулі. Сондықтан Тьюринг машинасын лентасы шексіз болғандықтан есептеу техникасы түрінде қолдануға болмайды.

Тьюринг машинасымен жұмыс істеу үшін объектілер туралы ұғымдарға тоқталу қажет.

Анықтама. Әлдебір алфавиттен алынған әріптердің кез келген тізбегі осы алфавитте сөз деп аталады.

Анықтама. Сөздегі әріптердің саны сөз ұзындығы деп аталады. Әріптері жоқ сөзді бос сөз дейді. Олар « 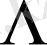» немесе 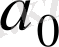деп белгіленеді.

Әлемдегі барлық объектілерді әртүрлі алфавиттегі сөздер түрінде қарастыруға болады. Сондықтан алгоритмнің жұмыс істеу объектілері сөздер болып табылады.

Анықтама. Алгоритм қолданылатын сөзді енгізілетін сөз дейді. Алгоритмнің нәтижесі шығарылатын сөз деп аталады. Алгоритм қолданылатын сөздердің жиыны алгоритмнің қолданылу облысы деп аталады.

Әрбір Тьюринг машинасында 2 бөлік бар:

Ұяшықтарға бөлінген екі жағынан да шексіз лента
Автомат - жазу/оқу инесі

Тьюринг тезисі: Кез келген алгоритм үшін сәйкес Тьюринг машинасын құруға болады.

Анықтама. Тьюринг машинасы деп 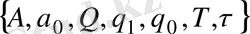жүйесін айтады. Мұндағы: А - шекті -жиын, Тьюринг машинасының алфавиті, 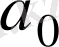- А алфавитінің бос сөзі, Q -Тьюринг машинасының жағдайын білдіретін шекті жиынның элементі, q ₁ - ТМ-ның бастапқы жағдайы, q ₀ - ТМ-ның тоқтау жағдайы, пассивті жағдай, Т-ТМ-ның жылжу жиыны, - ТМ-ның программасы.

Анықтама. Алгоритм (Тьюринг бойынша) - қойылған есепті шешуге келтірілетін Тьюринг машинасына құрылған программа.

Тьюринг машинасы мен тезисі болашақта да қолданылады, себебі кез келген проблема шешілмейді деп айтуға болмайды, шешілмейтін есеп болмауы керек, оны қандай да бір шешілетін түрге келтіру керек, соған орайластырылған алгоритм құрастыру керек.

Машинаның белгілі бір процесті орындауының өзі алгоритмдік процесс болып табылады. Сондықтан алгоритмге қойылатын талаптар мен қасиеттер оны орындайтын машинаға да қойылады:

Машинаның жұмысы дискретті, бірінен кейін бірі орындалатын жеке - жеке командалармен орындалуы керек.
Әрекеттер детерминделген, яғни қадамдар қатаң реттелген, ал олардың нәтижесі алдыңғы қадамда алынған нәтижелермен тікелей байланысты болуы керек.
Жұмыс алдында алғашқы берілгендер алгоритмнің анықталу облысынан алынуы керек.
Саны санаулы қадамдарды орындаудан соң нәтиже алынуы керек.
Машина универсалды, жан - жақты болуы керек, оның көмегімен кез - келген алгоритмді орындайтын болуы керек.

Сипатталған машинаның құрылғылары немесе структурасы қарапайым болса және орындалатын қадамдар элементарлы болса, алгоритмнің орындалуы машинаның жұмыс істеуі деп есептеуге болады .

Машинаның орындайтын қадамдары элементарлы болуы үшін белгілі бір алфавит арқылы ақпаратты алмастыру керек. Сондықтан алгоритм - кез- келген ақырлы алфавиттен берілгендерді немесе ақпаратты алмастыру

Ережелерінің ақырлы кез келген жүйесі.

Алгоритмнің анықталу облысынан алынған бастапқы берілгендер А алфавиті және ақырлы { 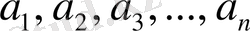}таңбалар тізбегін құрасын, мұндай тізбекті сөз дейді. Алгоритмді орындау барысында жаңа сөз құрылады { 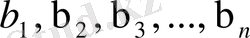}, олар В алфавитін құрайды. Бұл алмастыруды жүргізу үшін келесі қадамдар орындалады:

Бастапқысөзінің бір сөзін В алфавитінентаңбасымен алмастыру.
Бастапқы сөздің таңбасын өшіру.
В алфавитінен бір таңбаны бастапқы сөзге қосу.

Егер алфавитке «бос таңба» деп аталатын таңба қосылса, оны сөзге оң жағынан да сол жағынан да қоссақ та сөз өзгермейді, яғни 1) операция бос таңбаны алмастыру болады. Сонда 2) - 3) - операцияларды орындасақ та, бәрібір 1) - қадамда тағы сол алдыңғы қадам қалады. Сондықтан абстрактылы машина әр символды зерттейді, сосын шексіз лентаға - жадыға сақтайды, егер символ бос болмаса оны басқа таңбамен алмастырады да жаңа қалыпта тұрады.

Бұл машина туралы теорияны Алан Тьюринг (1936-1937), Эмиль Пост сияқты ғалымдар ұсынған. Осы принципке сәйкестелген есептеу машиналары 8-9 жылдан кейін пайда болған.

Пост алгоритмдік машинасы алгоритм ұғымын дәлелдеуші

Бұл машинаның Тьюрингтен айырмашылығы - ол өзінің теориясында «машина» емес «алгоритмдік жүйе» деген терминді қолданған.

Оның абстрактылы машинасы бірнеше бірдей секцияларға бөлінген, оқу-жазу инесі бар шексіз лентадан тұрады. Әр секция бос немесе толтырылған болуы мүмкін. Лентаға түк жазылмаса секция бос, лентаға жазылып белгі түссе секция толық деп есептеледі.

Лента жағдайы процесс уақытында өзгермелі болды. Осы лента жағдайы мен оқу-жазу инесінің орны туралы ақпарат Пост машинасының жағдайын айқындайды.

Инені « », метка-белгі М болсын. Секция бос болса, ешбір белгі түспейді. Бір қадам жасағанда ине оңға немесе солға 1 қадам жылжып белгіні салады немесе өшіреді. Программадағы командаларға сәйкес машина 1 жағдайдан келесі жағдайға көшіп отырады.

Әрбір команданың структурасы ХКУ болсын,

Х - орындалатын команда нөмірі,

К - орындалатын әрекет туралы нұсқау,

У - келесі команда нөмірі.

№

команда

Командалардың жазылуы

Машина әрекетінің сипаттамасы

№: 1

команда: Оңға қадам

Командалардың жазылуы: Х→У

Машина әрекетінің сипаттамасы: Инені оңға қарай 1 секцияға жылжыту

№: 2

команда: Солға қадам

Командалардың жазылуы: Х←У

Машина әрекетінің сипаттамасы: Инені солға қарай 1 секцияға жылжыту

№: 3

команда: Белгі салу

Командалардың жазылуы: Х V У

Машина әрекетінің сипаттамасы: Секцияға белгі қойылады

№: 4

команда: Белгіні өшіру

Командалардың жазылуы: Х x У

Машина әрекетінің сипаттамасы: Секциядан белгі өшіріледі

№:

команда: Басқаруды ауыстыру

Командалардың жазылуы:

Х У ₁

У ₂

Машина әрекетінің сипаттамасы: Секцияда белгі жоқ болса басқару у ₁ командасына, әйтпесе у ₂ командасына беріледі

№: 6

команда: тоқтату

Командалардың жазылуы: Х стоп !

Машина әрекетінің сипаттамасы: Машина жұмысын тоқтатады

№: 7

команда: Тармақты ұйымдастыру

Командалардың жазылуы: ? a; b

Машина әрекетінің сипаттамасы: Ұяшықты қарау, егер ұяшықта 0 тұрса, онда а номерлі командаға көшу, әйтпесе b нөмірлі командаға көшу.

Бұл әрекеттерге қойылатын қосымша шарттар:

ХМУ командасы бос секцияда орындалмайды
ХсУ командасы толық секцияда орындалады
У командасының нөмірі программадағы бар команда нөмірімен сәйкес болуы керек.

Егер келтірілген шарттар сақталмаса, онда машина нәтижесіз жұмысын аяқтайды. Х стоп командасы нәтижелі орындалады. Себебі, ол өзінің алдындағы әрекеттер орындалып барып солардың нәтижесінде орындалады. Кейде машина тоқтамауы мүмкін, егер командалардың ешқайсысында тоқтау командасына көшу нөмірі болмаса.

Пост машинасы оң бүтін сандарды жазуды қарастырады, себебі кез келген сөз цифр түрінде кодталады.

Лентада К бүтін саны К+1 келесі белгіленген секцияларда, унарлы санау жүйесі қолданылып жазылады.

0, 2, 3 сандарыныің жазылуы:

Өзін-өзі бақылау сұрақтары:

Пост алгоритмдік машинасы
Пост машинасының Тьюрингтен айырмашылығы
Тьюринг машинасына аАнықтама
Алгоритм абстрактілі машина іспеттес

3-дәріс: «Алгоритмдік шығарылмайтын есептер. Есептелетін функциялар»

Дәріс мақсаты: Алгоритмдік шығарылмайтын есептерді анықтау. Рекурсия ұғымын енгізу. Есептелетін функциялар ұғымын талдау.

есептелетін функция ұғымы
Рекурсия ұғымы, рекурсивті функция
Компьютер көмегімен есептелетін функциялар теориясы.
Черч тезисі

21-ші ғасырдың ортасына дейін алгоритм ұғымы есептеу әдістері ұғымымен теңестірілді. Есептеу әдістерінде қолданылатын арифметикалық, анализдік, тригонометриялық операциялардың орындалу алгоритм іспеттес болып жүрді. Ондай проблемаларды шешу үшін қосымша арнаулы дәлелдеулердің қажеті болмады. Ал 21-ші ғасырдың 2-ші жартысынан бастап сандық емес объектілерге қолданылатын алгоритмдерге қатаң формулировка берудің болмайтындығы белгілі болды. Лейбництің тұжырымдамасы бойынша алгоритмдік шешілмейтін есептер бар, сондықтан кез келген математикалық тұжырымдамалардың дұрыстығын дәлелдейтін алгоритм құрастыру қажеттігі туындады. Ол барлық теоремалардың дұрыстығын дәлелдейтін болуы керек.

Анықтама. Әлдебір алгоритм көмегімен есептелетін функцияны есептелетін функция дейді.

Іс жүзінде алгоритм - функцияны беру әдісі. Ал функция таблица, схема, формула түрінде берілуі мүмкін. Бірақ кейбір процестерде бастапқы енгізілген немесе берілген деректер мен алынған нәтижедегі деректер арасындағы байланысты ұйымдастыратын функцияны құру қиын, күрделі.

1 - бағыт Рекурсивті функциялар - есептелетін функциялар ұғымымен байланысты.

Рекурсия

Рекурсия ұғымы. Рекурсия деп көмекші алгоритм ретінде алгоритмнің өзін -өзі шақыруын айтамыз. Әдетте рекурсия едәуір қиын тақырыптарға жатады. Тақырыпқа деген қызығушылықты арттыру үшін «рекурсияны білу -дамыған ақыл-ойдың белгісі» деп айтуға болады. Сонымен рекурсияның оқытуды бірнеше деңгейде бөліп оқытуды ұсынамыз.

Бірінші деңгейде (танысу) . Балаларға арналған лого тілінде рекурсия бастапқы кезеңде “Жұлдызша ’’алгоритмді (шексіз мөлшерде орындалатын) түрінде беріледі. Бұл жерде оқушы қайталану мен рекурсияның айырмашылығын түсіне алмайды. Сурет салу процесін тоқтату үшінCTRL-STOP клавишалары пайдаланылады.

Екінші деңгей (түсіну) . Рекурсияның мағынасын шарт бойынша тексерілетін алгоритмді мысалға келтіре отарап шашып беруге болады. Бұл өзінөөзі шақыру процесінің әйтеуір аяқталуы мүмкін деген тұжырым жасауға әкеледі. Мысал ретінде Роботтың экрандағы жүрісін алуға болады.

Үшінші деңгейде(меңгеру) . Аса қызықты да, маңызды жағдай- анргументінің басқа мәндерінде өзі арқылы анықталатын аргументті функциялар. Мысалы, tg(х) функциясы tg(х/2) арқылы өрнектеледі, бірақ бұл шексіз рекурсия. Функцияның рекуурсивті анықталуының классикалық мысалы - факториал:

Алг бүт факт(бүт N)

Арг N

Нәт F

Басы

Егер N=0

Онда мән:=1

әйтпесе мән:=N*F(N-1)

бітті

соңы

Егер бұл жазуды маематикалық анықтама ретінде қарастыратын болсақ, онда бәрі де түсінікті. Егер шақырудың орнына команданың орнына қою әдісін қарастыратын болсақ, онда мынандай тізбек аламыз:

F(3) =3*F(2) =3*(2*F(1) ) =3*(2*(1*F(0) ) ) = 3*(2*(1) ) =3*(2) =2

Солдан оңға қарай оқиық. Орындалу әрекеті жақшаменг көрсетілген. Мұндағы қиындық көбейтуді есептеудің оң жақтағы функция көбейткішін есептегенше, кенйінге қалдырылғанында болып отыр.

Бұдан да айқынырақ тәсіл - ұлғаймалы параметрлі рекурсивті функциялар. Әдістің мақсаты - функцияны формуладан шығару, амалдарды кейінге қалдырудан құтылу. Бұл программалау тілдерінде жеңілдетеді. Сонымен, факториалды былай есептеуге болады:

Алг бүт FP( бүт N, R)

Басы

Егер N=0

Онда мән:=R ! өзін шақырдың соңы

әйтпесе мән:=FP(N-1, R*N)

шақыруға дейінгі көбейту

бітті

соңы

Енді әрекетте кейінге қалдырылмай (солдан оңға қарай оқимыз) :

F(3, 1) =F(2, 3*1) =F(1, 2*3) =F(0, 6) =6.

Қорланатын параметрлер әдісінде цикл инвариантымен аса маңызды ұқсастық бар: N аргумент пен R қорлану коэффициенті сәйкес өзгереді.

... жалғасы