Қатты денелер физикасы

Жоспар
Кіріспе

Кіріспе
I тарау
1 Қатты дененің ішкі құрылымы. Кристалл торы
2 Қатты денелердегі анизотропия Моно және поликристалды катты денелер
3 Химиялық элементтердің кристалдық құрылымдары
4 Полиморфизм құбылысы
5 Кристалдардағы құрылым жетіспеушілігі
(құрылым кемшілігі) және ақаулар
6 Адиабаталық жуықтау. Реттелген
және реттелмеген күйлер. Жылулық қозғалыс.
7 Кристалл электрондардың динамикасы
8 Дебай Теориясы бойынша түсінік
9 Заттардың магниттік қасиеттері.

Техниканың өсуіне физиканың ролі күннен-күнге өсу барысында десек артык айтканымыз болмас, әсіресе катты денелер физикасы. Жартылай өткізгіштер техникасынын, кванттық электрониканың, қажетті механикалык, электр, магнитгік, оптикалық жэне басқа касиеттерге ие жаңа материалдарды алу жолдарындағы жетістіктер катты денелер физикасының даму нәтижелерімен үздіксіз байланыста. Барлық өндірістердегі болатын келешектегі техникалық прогресті әр түрлі приборлардағы және қондырғылардағы технологиялық процестер анықтайды, ал бұл технологиялык процестер катты денелердегі өтетін кұбылыстарға негізделген. Бүл бағытта көптеген мысалдар келтіруге болады,
Сондықтан катты денелер физикасын окып-білу тек физиктерге ғана емес, өндіріске тікелей катысы бар инженер, инженер-технологтарға да өте кажет.
I тарау
Қатты дененің ішкі құрылымы
Кристалл торы
Қатты денелердін ішкі қүрылымын сипаттау үшін кеңістік немесе кристалл торы деген түсінікті енгізу ынғайлы.
Кристалл торы кеністік торын күрайды, тордың түйінінде

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:

Қатты денелер физикасы

Кіріспе
Техниканың өсуіне физиканың ролі күннен-күнге өсу барысында десек артык
айтканымыз болмас, әсіресе катты денелер физикасы. Жартылай өткізгіштер
техникасынын, кванттық электрониканың, қажетті механикалык, электр,
магнитгік, оптикалық жэне басқа касиеттерге ие жаңа материалдарды алу
жолдарындағы жетістіктер катты денелер физикасының даму нәтижелерімен
үздіксіз байланыста. Барлық өндірістердегі болатын келешектегі техникалық
прогресті әр түрлі приборлардағы және қондырғылардағы технологиялық
процестер анықтайды, ал бұл технологиялык процестер катты денелердегі
өтетін кұбылыстарға негізделген. Бүл бағытта көптеген мысалдар келтіруге
болады,
Сондықтан катты денелер физикасын окып-білу тек физиктерге ғана емес,
өндіріске тікелей катысы бар инженер, инженер-технологтарға да өте кажет.

I тарау
Қатты дененің ішкі құрылымы
Кристалл торы
Қатты денелердін ішкі қүрылымын сипаттау үшін кеңістік немесе кристалл
торы деген түсінікті енгізу ынғайлы.
Кристалл торы кеністік торын күрайды, тордың түйінінде бөлшектер (атом,
молекула) орналаскан болады, сонымен катты денені құрайды

І.І.-сурет

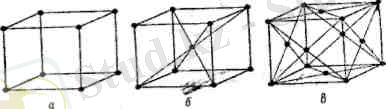
Қалың сызықпен ен кіші параллелепппед көрсетілген, бұл параплелепипедтің
озінің үш осі бойынша орын ауыстыруымен барлық кристалды құруға болады. Бүл
параллелепипедті элементар немесе негізгі тор ұяшығы деп атайды. Бұл тор
ұяшығын сипаттау үшін 6 шаманы беру керек: үш қырын {а, е, с) және осьтер
арасындағы бұрыштарын (α, β, γ). Бүл шамаларды тор параметрлері деп атайды.
Қарапайым тор түріне куб торы жатады, мұнда а = в = с жэне α= β = γ = 90°.
Кейбір жағдайда тордың симметриясын нақты айкындау максатында элементар тор
шыңдарында ғана орналаспай, тағы тор үяшығының басқа нүктелерінде де
орналасқан болады. Мысалы, көлем центрленген торда кеңістік
диагональдардың қиылысқан нүктесінде қосымша бір бөлшек орналасқан болады
(1.2.б -сурет), жақ центрленген торларда жақ диагональдарының қиылысқан
нүктелерінде косымша бөлшектер орналасқан болады (І.2.в -сурет), т.б. Енді
түйіндерді, бағыттарды және тордың жазықтықтарын белгілеуді қарастырайық.
Бұл белгілеулерді Миллер индекстері деп атайды.

1.2.- сурет

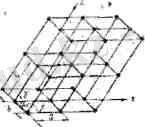
Тор индекстері. координата басынан алынған кез-келген тор түйінінің

орнын оның х, у, z координатасымен анықтайды. (І.З.-сурет)

1.3-сурет 1.4-
сурет

x = ma, y = nb,
z = pc (1.1)

,

Мұндағы : а, Ь, с – тор параметрлері, т, п, р - бүтін
сандар.
Ось бойымен өлшенетін бірлікті метр деп есептемей, бірлік ретінде тордың а,
Ь, с параметрлерін алсак, онда тор координаталары т, п, р бүгін сандар
болады. Бүл сандарды түйін нндекстері деп атайды және былай жазылады:
[[mnр]]. Теріс индекс болса, теріс таңба индекс төбесіне қойылады:
[[mn'р]].
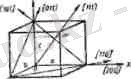
Бағыт индекстері. Кристалдағы бағытты сипаттау үшін координата басынан
тура сызық алынады. Ол сызықтың орналасуын бірінші .түйіннің тор индексі
аныктайды, сызық сол бірінші түйіннен өтеді (І.З.-сурет). Сондыктан
түйіннің тор индекстері бағыт индексі де болады. Бағыт индексін [mқр] -мен
белгілейді. Бағыт индексінін аныктамасы бойынша, оны үш ен кіші бүтін сан
анықтайды. Мысалы, координата басынан және [[345]] түйіннен өтетін бағыт
индексі [345] болады.
Мысал ретінде куб торының негізгі бағыттарын көрсетуге болады (1.4.-
сурет). Тор осьтерінің индекстері: ОХ осінің индексі [100], ОУ осінің -
[010], 02 осінің - [001]. Жақ диагональдарының индексі: вс жағы
диагоналының
индексі [011], ас жағы диагоналының - [101], ав жағы диагоналының [110],
кеңістік диагоналының индексі - [111].
Кристалл жақтарының индскстері. Кристалл жақтарының орнын кристалл торының
осьтерін қиып өтетін А, В,С кескіндер анықтайды. Мұндай жазық теңдеуінің
түрі мынадай болады:
XA+YB+ZC=1
(1.2)
Мұндағы X. У, Z- осы жазықта жататын нүктенің координаталары. Егер кристалл
жазығы (жағы) тор түйінінен ететін болса (тек сондай жақтар қарастырылады),
онда жазықта жататын кез-келген түйіннің координаталары түйін нндекстеріне
тең:
x=m, y=n, z = р.
Сондықтан жазық теңдеуін мынадай түрде жазамыз:

m1A+n1B+p1C=1 (1.3)

т, п. р бүтін сан болғандықтан. (1.3) теңдеу 1А, 1В, 1С қатынастар
рационалды сандар болуы керек, олардың қатынастарын h,k,l үш бүтін сан
қатынастарымен ауыстыруға болады;

1A:1B:1C=h:k:l (1.4)

Осы h,k,l сандар кристалл жазықтарының индекстерін береді олар былай
белгіленеді (h,k,l). Жазық индекстерін былай анықтайды: тор осьтеріндегі
жазықты қиып өтетін ось бірлігімен алынған А, В, С кескіндерді сол
кескіндердің кері мәндеріне сәйкес, яғни 1А, 1В, 1С етіп жазады. Алынған
1А, 1В, 1С бөлшектерге ортақ бөлім табады. Ортақ бөлім Д болсын дейік,
онда бірінші бөлшекке ДА, екіншіге ДВ, үшіншіге ДС болады. ДА, ДВ, ДС
бүтін сандар кристалл жазығының h,k,l индекстері болады. Яғни

h=ДA, k=ДB, l=ДC
(1.5)

Мысалы:
I. Тор осьтерін қиып өтетін А=1, В=2 және С-3 кескіндерге сәйкес кристалл
жазықтығының индексін анықтайық.
Шешім: 1A:1B:1C = 11:12:13 - рационал сандар, онда жалпы бөлгіш
болады. Олай болса, 61=6, 62=3, 63=2, яғни h=6, k=3, l=2, жазық индексі
(632) болады екен.
2. Тор осьтерін қиып өтетін А=12, В=2 және C=13 кескіндерге сәйкес
кристалл жазығының индексін анықтайық.
Шешім: 1A:1B:1C=112:12:113-рациона лды сандар. Ортақ бөлім 2
болады,онда h=212=4, k=22=1, l=213=6 жазық индексі (416).
(1.5) қатынастан тор осінен өтетін кескінді сол жазықтың индексімен
анықтауға болатыны көрініп тұр, яғни
A=Дh, B=Дk, C=Дl (1.6)
Сондықтан жазық индексі (hkl) арқылы тор осьтерін қиып өтетін
кескіндерді анықтау үшін индекстердің кері мәнін жазып. яғни 1h,1k,1l,
олардың ортақ бөлімін (Д) анықтайды. Онда (1.6) теңдеулер
арқылы кескіндер анықталады: А=Дh,В=Дk,С=Дl
3. Тор осіндегі (123) жазықты қиып өтетін кескіндерді анықтайық.
Шешім Жазық индекстнрінің кері мәнін жазамыз: 11, 12, 13. Онда кескінде
А=61=6, В=62=3, С=63=2 тең. Координат осьтеріне параллель жазыққа
сәйкес индекс нольге тең.

Қатты денелердегі анизотропия Моно және поликристалды катты денелер

Қатты денелердің бөлшектері кристал торында біртекті қатар-қатар
орналасқан деп есептейік (Кристалдардағы ақауларды ескермейміз). О
нүктесінен ОА, ОВ, ОС, т.б. бағытта сызық өткізейік. Әрбір бағытта бірлік
арақашықтықта кездесетін бөлшектер саны әртүрлі жиі кездесетін бөлшектер ОА
бағытта, ал сирек кездесетін бөлшектер ОС бағытта. Әрбір бағыттағы қатты
денелердің қасиетгерін бөлшектердің сол бағытта қаншалықты тығыз орналасуы
анықтайтын болғандықтан, алынған бағыт бойынша қатты денелердің қасиеттері
әр түрлі болуы керек. Дене қасиетінің бағытқа тәуелділігін (қасиеттің.
бағыттылығын) анизотропия деп атайды. Арнайы жағдайда қатты денелерді бір
кристалл түрінде өсіруге болады, яғни монокристалл түрінде. Бірақ көп
жағдайда ерітінділерде (балқыған денелерде) бір мезгілде көптеген
кристаллизацияланатын орталықтар пайда болып, көптеген өзінше бөлек
кристалдар болуына алып келеді. Бұл кристалдардың өсуінің арқасында олар
бір-біріне жақындай түседі. Сонымен көптеген бөлшектер пайда болады, яғни
поликристалл. Өскен кристаллиттер (дәндер) әр түрлі формада болады, сыртқы
көрінісі ішкі ретті құрамына сәйкес келмейді. Себеб! олардың (дәндердің)
орналасуы суытылған ерітіндіде (сұйық күйдегі затта) кристаллизация
орталығы кездейсоқ орналасқан болады, өскен дәндердің өзара орналасуы да
кездейсоқ болады. Сондықтан поликристалдарда олардың қасиеттері кристалл
бағытына елеулі тәуелді болуы байқалмайды, яғни олар изотропты болады.
Сонымен қатар өскен дәндердің әр түрлі бағытта болғандағы дәндер
(кристаллиттер) шекарасында кристаллиттер шекарасы деп аталатьгн әр түрлі
қалыңдыққа ие қабаттар пайда болады. Бұл дән шекаралары поликристалл
агрегатының механикалық қасиетінің қалыптасуына елеулі әсер етеді. Өте
таза, қоспа атомдардың болуы жақтың қасы болғанда да дәнаралық қабатындағы
тор дән торына қарағанда елеулі ауытқыған болады. Бұл тор ауытқуы бір атом
аралығымен шектелмейді, бірнеше атом аралықтарына дейін орын алады. Бұл
торлары ауытқыған атомдармен дән шекарасындағы атомдар бір-бірімен
әсерлеседі. Дән шекарасындағы ретсіздік дәрежесі үлкен (жоғары) болған
сайын, ретсіздік көлемі(ретсіздік
қабыршақтың қалыңдығы - ені) үлкен болады және олардың тор ауытқулары
ұлғаяды, яғни тор ауытқу дәрежесі өседі. Кристаллит тор жолағындағы
ауытқулар, бұл жолақта артық еркін энергияның шоғырлануына (локализация)
алып келеді. Еркін энергияның шоғырлануы бірнеше тәжірибелерде дәлелденген.
Сонымен қатар өскен дәндердің әр түрлі бағытта болғандағы дәндер
(кристаллиттер) шекарасында кристаллиттер шекарасы деп аталатьгн әр түрлі
қалыңдыққа ие қабаттар пайда болады. Бұл дән шекаралары поликристалл
агрегатының механикалық қасиетінің қалыптасуына елеулі әсер етеді. Өте
таза, қоспа атомдардың болуы жақтың қасы болғанда да дәнаралық қабатындағы
тор дән торына қарағанда елеулі ауытқыған болады. Бұл тор ауытқуы бір атом
аралығымен шектелмейді, бірнеше атом аралықтарына дейін орын алады. Бұл
торлары ауытқыған атомдармен дән шекарасындағы атомдар бір-бірімен
әсерлеседі. Дән шекарасындағы ретсіздік дәрежесі үлкен (жоғары) болған
сайын, ретсіздік көлемі(ретсіздік қабыршақтың қалыңдығы - ені) үлкен болады
және олардың тор ауытқулары ұлғаяды, яғни тор ауытқу дәрежесі өседі.
Кристаллит тор жолағындағы ауытқулар, бұл жолақта артық еркін энергияның
шоғырлануына (локализация) алып келеді. Еркін энергияның шоғырлануы бірнеше
тәжірибелерде дәлелденген.

Химиялық элементтердің кристалдық құрылымдары

Қатты күйдегі химиялық элементтер ішкі ретті құрылымды кристалдық
денелерді құрайды. Кристалл құрылымының түрін негізінен құрылым
бөлшектердің (атомдар, иондар, молекулалар) арасындағы байланыс күштің түрі
анықтайды. Бұл бөлшектер арасында 4 негізгі байланыс болғандықтан 4 типті
кристалл торын кұрайды: ионды немесе координационды тор, бұл торда атомдар
арасындағы негізгі байланыс ионды болады; поляризационды немесе молекулярлы
тор; мұндағы молекулалар арасындағы байланыс Ван-дер-Вальс күштері арқылы
болады; валентті байланысты атомдық тор және металды байланысты металл
торлары болады. Таза бір күш түрмен байланысқан, яғни өзара әсерлесетін
атомдарды сирек кездестіретін секілді, құрылым түрлерінде де таза бір типті
тордың кездесуі де өте сирек. Көп жағдайда тор өткінші (переходной) болып
келеді, яғни тордың өткінші болуы атомдар арасындағы байланыстың түрі екі
немесе бірнеше болудың арқасында химиялық элементтердің кристалдық
құрылымын жобамен 4 классқа бөлуге болады (1.1 .-кесте)

IА IIА ША

Бұл кұрылымдарды талдауды IV класстан бастаған ыңғайлы. Бұл. классқа
инерт газдардың кұрылымы жатады. Инерт газдардың сұйық күйге және кристалға
айналғанда электрондары симметриялы сфералық қабыршақтары бар атомдар
арасындағы байланыс әлсіз Ван-дер-Вальс күштің пайда болуынан болады. Бұл
күштің әсерінен симметриялық атомдар тығыз орналасқан жақ цеитрленген куб
торын құрайды (1.2.-сурет).
Тордағы әрбір атомды оған жақын орналасқан 12 атом қоршайды. Атомға жақын
орналасқан атомдардың санын тордың координациялық саны деп атайды.
III класс. Бұл классқа қысқа периодтан кремний және көміртегі IVВ топтан
германий және қалайы және VВ, IVВ және VIIВ топтардағы барлық элементтер
жатады. Бұл класстағы барлық элементтер 8-N ережесіне сәйкес
кристаллизацияланады, яғни тордағы әрбір атом 8-N жақын атомдармен
қоршалған.
I класс. Бұл классқа көп элементтер жатады, олар - металдар. Металл
торларында атомдар емес, олардың иондары орналасқан. Олар инертті газдар
секілді сфералық симметрияға ие. Сондықтан металдар кристаллизация кезінде
инертті газдар секілді тығыз орналасқан торға ие деп күтуге болады. Шынында
да, металдар 3 турлі кристалл торларына ие, Координациялық саны 12 тең жақ
центрленген куб (1.2. в-сурет), координациялық саны 12 тең гексагональды
тығыз орналасқан тор (1.6.-сурет) және 8 координациялық санға тең көлем
центрленген куб (1.2, б-сурет). Бұл ең ұлпа торлы металл (кеңістікті
атомдармен толтыру мағынасында). Идеал гексагональды торда са= 1,633 тең.
II класс. Бұл класстағы химиялық элементтер металл мен III класстағы 8-N
ережемен кристаллизацияланатын элементтер арасындағы аралық кристалдарға
жатады. IIВ топтағы Zn, Сd, Нg металдар, олай болса олар жоғары
координациялық санға ие металл торларының біріне жатуы керек. Ал шындығында
Zn және Сd кристаллизацияланғанда ерекше гексагональды компакты кұрылымға
ие болады. са--1,633 болмай, бұл қатынас 1,9 тең болады.
Полиморфизм құбылысы

Бірнеше қатты денелерді екі және оданда көп кристалдар құрылымына
және қасиеттерге ие, әр бір құрылым әр түрлі температурада және қысымда
тұрақты болады. Мұндай құрылымдарды политромды форма немесе заттың
модификасы деп атайды, ал бір модификациядан екінші модификацияға өтуді
полиморфты түрлену деп атайды.
Полиморфты модификацияны грек арібімен белгілеу қабылданған: қалыпты
және жоғары температура тұрақты модификацияларды сәйкесінше β, γ, τ және
т.б. әріптермен белгілейді. Полиморфизмге классикалық мысал ретінде
қалайыны алуға болады. 13,30С температурадан төмен температурада қалайының
α модификациясы тұрақты болады, бұл кезде қалайының құрылымын алмаз типті
тетрагональды куб торға ие. Бұл қалайыны сұр қалайы деп атайды. Мұндай
құрылымды қалайы морт болып келеді және ұнтаққа айналып оңай қирайды.
Бұрыңғы кезде көп заттар қалайыдан жасалған (мысалы, әскери киімдердің
түймелері, т.б.) төмен температурада заттардың бетінде бөлшектердің пайда
болуы және заттың төменгі температурада ұнтаққа айналып, қирауын байқаған,
бұл құбылысты түсінбегендіктен, металдың белгісіз ауруы деп қалайыны чума
деп атаған. Қалайыдан басқа полиморфизм қасиетіне көптеген басқада химиялық
элементтерге ие. Мысалы: көміртегі, темір, никель, кобальт, т.б. сонымен
қатар көп теген химиялық қосындылар және қоспалар. Теориялық көзқарас
бойынша, полиморфизм қатты денелерде болуы керек еді, егер олардың қатты
күйде тұрақты болып қалу мүмкіндігі олардың балқу және сублемация
процестерімен шектелмеген болғанда. Полиморфизм құбылысының болуын
кристалды қыздырғанда немесе қысыммен әсер еткенде атомдардың қозғалу
интенсивтілігінің өзгеруінің арқасында және атомдар қашықтығының өзгеруі
кристалл тордағы атомдар арасындағы байланыс күшінің және оның
интенсивтілігінің өзгеруіне алып келуіне байланысты, басқаша айтқанда
температура мен қысым атомдардың қозғалысы, атомдар арақашықтығын
өзгертеді, ал бұл өзгеріс атомдар арасындағы күшті және оның
интенсивтілігін өзгертеді, ал бұл өзгеріс атомдар арасындағы күшті және
оның интенсивтілігін өзгертеді, ал бұл өзгерістер полиморфизм құбылысын
алып келеді. Абсолют ноль температурасы аумағындағы тұрақты құрылымда
атомдар арасындағы күш байланыс ең жоғары болуы керек Менделеев кестесінде
қалайы IV-ші топта орналасқан, мұнда құрылым алмаз құрылымы болады, яғни әр
бір атом валентті 4 атомнан бағытталған күшті байланысты. Бір-ақ
температура жоғарылаған сайын байланыстың бағытталғанынан және қаттылығынан
жылу қозғалысының әсерінен байланыс оңай қирайды және 1,330С температурадан
жоғарылағаннан бастап валентті электрондар жалпылануының арқасында иілген
металдың байланысқа өтуі тиімді болады. Бұл металды байланысқа
тетрогональды көлем концентрленген (А3) тұрақты кристалл құрылымы сәйкес
келеді.
Бұл құрылым модификациясынан екінші модификацияға өтуі (түрленуі)
жылу шығару немесе жылу жұту арқылы болады. Сондықтан бірінші типті
фйазалық өту орын алады. Мұндай өту түрінің орын алуы тордың түрленуінен
байланысты, ал қатты заттағы атомдарының қозғалу мүмкіндігі төмен,
сондықтан бұл жағдайдағы термодинамикалық тұрақсыздық шектелмеген уақыт
аралықында болады. Мұндай құрылымның түрленуіне алмаз құрылымы 100000
температурады 20000С температурадан жоғарыда пайда болып және бұл құрылым
тұрақты болады. Бір-ақ алмаздың бөлме температурасына дейін суытсақта,
алмаз құрылымды көп уақытқа дейін болады, бөлме температурасында тұрақты
модификациясына айналмай қала береді. Айта кету қажет, қазіргі кезде
графиттен жасанды түрде алмаз алатын өндірістік технологиялық процес
анықталған.
Практикада полиморфизмнің ролі үлкен. Әр түрлі болаттарды және
қоспаларды алуда оларды термиялық өңдеуде және тағы көптеген технологиялық
процестер полиморфизм құбылыстарын қолдануға негізделген.

Кристалдардағы құрылым жетіспеушілігі
(құрылым кемшілігі) және ақаулар

Мозайкалық құрылым.
Нақты кристалдардың құрылымын зерттеудегі көптеген мәліметтерге
қарағанда, олардың ішкі құрылымы идеал кристалдардың құрылымнан елеулі
айырмашылығы бар екенін анғартады. Біріншіден, нақты кристалдардың құрылымы
мазайкалық құрылымға ие кристалл тура құрылымды блоктардан құралған блоктар
жобамен бір-біріне параллель болып келеді.
Бұл тор кемшілігі дән шекараларында жоғары болады, себебі бір дәннің
бағытталуы екінші дәннің бағытталуынан айырмашылығы он шақты градусқа ие.
Дән және блок шекаралары артық еркін энергияға ие болғандықтан,
химиялық реакцияның полиморфты түрленудің, диффузия процестерінің өту
жылдамдығы жоғары болады.
Қоспалар. Қоспалар нақты кристалдардың ішіндегі ең мәнді және құрылым
ақаулары көп тараған болып келеді. Ең таза қоспалардың 10-7 % құрайтын
химиялық элементтердің 1 см3 көлемінде 103 қоспа атомдары бар.
Қоспалардың табиғатына және молшеріне байланысты олар кристалдарды
ерітілген күйде немесе азды-көпті үлкен бөлшектерді құрайды. Кристалда
ерітілген қоспалар дегеніміз – қоспа атомының негізгі атомдар арсына енуі
немесе тордағы негізгі атомның орнына орналасуы. Бірінші жағдайдағы қатты
еретінді ерітілген деп, ал екінші жағдайдағы қатты ерітіндіні орын басу деп
атайды. Бөгде атомдардың физикалық табиғаты және өлшемі кристалдың негізгі
атомдарының ерекшелігі болғандықтан олардың кристалда болуы кристалл
торларын өзгертеді, яғни құрылым кемшілігі пайда болады.
Қоспа атомдар қатты денелердің химиялық, оптикалық, магниттік және
механикалық қасиеттеріне елеулі әсер етеді. Қоспа атомдар және механикалық
қасиеттеріне елеулі әсер етеді. Қоспа атомдар топ тасымалдайтын
бөлшектердің эффективті шашырататын орталық болады, яғни нақты дененің
электр кедергісін ұлғайтады, бұл кедергі абсолют ноль температурада да орын
алады. Жартылай өткізгіш кристалдарда қоспа атомдар жаңа энергетикалық
деңгейлерді тудырады, соның арқасында қоспа электр пайда болады.
Фотондар. Қатты денелердің атауларын үздіксіз тепе теңдік орнын қолында
(тор түйінінде) тербеліп тұрады. Сондықтан тордың дәл периодтылығы
бұзылады. Айта кету қажет, бұл тордың бұзылуын лездік деп түсіну керек.
Орташа уақытта тордың периодтылығы сақталады атомдық тербелісі тек тор
түйінінен кескінделеді.

Адиабаталық жуықтау. Реттелген
және реттелмеген күйлер. Жылулық қозғалыс.
1. Еркін электрондар моделі.
Қатты дененің электрлік және магниттік қасиеттерін анықтау үшін
түсіндіретін жақсы теория еркін электрондар теориясы болып табылады. Бұл
теория бойынша металл ішіндегі еркін электрондар барлық көлем бойынша орын
ауыстыра алады. Металл ішіндегі заряд бір қалыпты Р-мен таралған потенциялы
+V0 өріс жасайды. Көптеген есептерде бұл потенциал 0-ге тең деп есептеледі
және еркін электрондардың тек кинетикалық энергиясы бар деп ұйғарылады.
Металдың бетінде потенциял V0 ден 0ге дейін кемиді. Ал электрон
потенциалдық энергиясы V0=-eV0 ден 0ге дейін артады (1-сурет).
Бұл жағдай металды потенциалды шұқыр ретінде қарастыруға мүмкіндік
береді потенциалдық шұқыр үшін Шредингердің теңдеуі:

R2 – толық вектор.
е – электрон энергиясы
е – нің R-ға байланысты графигі (2-сүретте) к
көрсетілген. Ол парабола болады.
Электрон ось еркімен металдан шығып кете алмайтын, металдың
шекарасында (х=0 және х=L) толқындық
функция 0-ден өзгешще болуы тиіс.
Сондықтан шекара шарттары немесе (3)
Бұл шарттарды қанағаттандыратын шешімдер мынадай
(4)
мұндағы (5)
және (5)-ті (2)ге қойсақ металдағы еркін электронның энергиялық
спектрін анықтаймыз.
(6)
(6) дан спектрдің дискреті екендігін көреміз.
Қатты дене теориясында (3) шекара шартының орына периодтық шекара
шарттары қолданылады. Қатты дене шексіз үлкен деп есептеледі, ол оның
сипатталымы периоды L ға периодтық функция ретінде қарастырылады. Басқаша
айтқанад, шексіз үлкен қатты денені қыры L-ға тең кубиктерге ойша бөледі
және Ψ –дің өзгеру заңы кубикте қайталанып отырады. Шексіз үлкен дене
электронның қозғалысы мынадай толқындармен Ψ=АeiRx сипатталынады, олар
еркін микро бөлшектер үшін Шредингер теңдеуінің шешімі болып табылады.
Толқындық функцияның периодтылығы талабынан
(7)
Шредингер теңдеуінің шешімі мынадай. Ψ=АeiRx екендігін ескерсек, және (7)
формулаға қойсақ, онда
осыдан
Бұл теңдеу R-ның радиусының тек мынадай мәндерінде

орындалатындығын көреміз, осы (8) (2) онда
(9)
Сонымен периодты шекара шарттарда энергетикалық спектрдің
дискреттілігін көрсетеді. Электронның деңгейлері бойынша таралуы Ферми –
Дерак статистикасы бойынша сипатталады.
Еркін электрондар моделі жуық модель болып табылады. Бұл модель қатты
дененің құрылымын ескермейді, оң зарядтың диспектірі таралуында ескермейді.
Бұл модельді электронның тор түйіндемелерімен әсерлесетін тек тұрақты
өріспен айрбастайды. Бір-ақ осыған қарамастан еркін электрондар теориясы
металдағы электрондық газдардың негізгі қасиеттерін анықтауға мүмкіндік
береді, электр және жылу өткізгіштің температураға байланыстылығы нақты
олардың обсалюттік шамаларын бағалады. Электронның эмиссия құбылысымен
байланысты құрылыстарды сипаттайды және тағы басқа.
Электрондық теорияның келесі даму этапы қатты дененің зоналық
теориясы болып табылады. Зоналық теорияда қатты дене кристалдық дене
ретінде қарастырылады. Кристалл дұрыс формалы ішкі құрылымға ие болады.
Осындай кристалдағы электрондарды сипаттау үшін 2 жуық әдістемелері бар.

Кристалдарда электрондардың күшті байланыс жуықтауы.
Бұл әдіс бойынша кристалдарда жекелеген атомдардың саны өте көп деп
есептелінеді. Әр бір атомның энергиясы дискретті энергетикалық деңгейлерге
ие болады. Электронның атом мен байланыс энергиясы сол энергетикалық тордың
ішіндегі кинетикалық энергияларынан көп болады. Сондықтан, электрон өзінің
көп уақытын атомның маңайында немесе жанында болады, ол аз уақытын бір
атомнан екінші атомға орын ауыстыруына жұмсайды. Бұл әдістің
негізінде жекелеген атомдардың толқын-
дық функциялары енгізіледі. Содан кейін
электронның толқындық функциялары табылады. Атомның энергетикалық күйін
энергетикалық деңгейер арқылы кескіндеу ыңғайлы.

Салыстырмалы Деңгейдің Азғындалуының Ішкі деңгейдің
энергия белгіленуі еселігі саны

6d 10 6
7p 6 3
7s 2 1
4f 14 7
5d 10 5
6p 6 3
6s 2 1
4d 10 5
5p 6 3
5s 2 1
3d 10 5
4p 6 3
4s 2 1
3p 6 3
3s 2 1
2p 6 3
2s 2 1

1s 2 1

n=1, s=0,
l = 0, 1, 2, 3
s, p, d, f

Еркін атомды электронның энергиясы бас кванттық санмен n және
азимутальды кванттық санмен L анықталады. Бір-ақ, ол энергия магниттік
кванттық сан m және спильдік кванттық сан S-ке байланысты болмайды. Сол
себепті әрбір энергетикалық деңгейде 2(2L+1) әр түрлі электронның күйлері
сәйкес келеді. Бір-ақ, электрондардың спинді электронының энергиясына әлсіз
әсер еткендіктен спиндері қарама- қарсы болатын күйлері бірдей энергияға ие
болады. Сондықтан энергетикалық деңгейлер 2(2L+1) емес, тек 2L+1 ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.