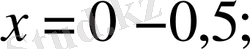Мәндес түрлендірулерді теңдеулерді шешуде қолдану және орта мектепте оқыту әдістемесі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 67 бет
Таңдаулыға:
Диплом жұмыстың тақырыбы: Мәндес түрлендірулерді теңдеулер шешуге пайдалану.
МАЗМҰНЫ
КІРІСПЕ . . . 3
1. ТЕҢДЕУ ТУРАЛЫ ЖАЛПЫ МӘЛІМЕТ
1. 1 Теңдеу, теңдеудің шешімдері . . . 6
1. 2 Теңдеу шешудегі мәндес түрлендірулер . . . 11
1. 3 Квадрат теңдеулер шешудің әдістері . . . 17
1. 3. 1 Квадрат теңдеудің даму тарихы . . . 17
1. 3. 2 Квадрат теңдеулерді шешудің 10 әдісі . . . 19
2. ТЕҢДЕУ ШЕШУДІ. ОҚУШЫЛАРДЫ ТЕҢДЕУ ШЕШУГЕ ҮЙРЕТУ. МӘНДЕС ТҮРЛЕНДІРУЛЕРДІ ҮЙРЕТУ
2. 1 Рационал теңдеулер шешуде мәндес түрлендірулер . . . 27
2. 1. 1 Рационал теңдеулер шешуде мәндес түрлендірулер . . . 27
2. 1. 2 Иррационал теңдеулер шешуде мәндес түрлендірулер . . . 30
2. 2 Тригонометриялық теңдеулерді шешуде мәндес түрлендірулер . . . 32
2. 3 Логарифмдік теңдеулерді шешуде мәндес түрлендірулер . . . 39
2. 4 Компьютерлік технологияны теңдеулер шешуде тиімді пайдалану . . . 43
2. 5 Мәндес түрлендірулерді теңдеулер шешуде пайдаланып, компьютерде модельдеп оқыту әдістері . . . 50
ҚОРЫТЫНДЫ . . . 52
Пайдаланған әдебиеттер . . . 53
К І Р І С П Е
Жаңа әлемдегі жаңа Қазақстанды құру бізден жеке адамдардың, қоғамның және еңбек нарығының талаптарын қанағаттандыра алатын бәсекеге қабілетті білім беру жүйесін қалыптастыруды талап етеді.
Тәуелсіздіктің ертеңі оқу-білімнің тереңділігімен өлшенеді. Еш толас- сыз, үздіксіз өзгеріп тұрған әле
м адамынан да қабілет пен қажеттіліктерді толассыз, үздіксіз дамытуды талап етеді.
Елбасымыз Н. Ә. Назарбаевтың “Қазақстан-2050” даму бағдарламасын- да Қазақстан халқына арналған жолдауында “Біздің жас мемелекетіміз өсіп, жетіліп кемелденеді, жас шәкірттер онымен бірге ер жетеді. Олар өз ұрпағының жауапты да шегерлі, білім өрісі биік денсаулықтары мықты өкілдері болады” деп көрсеткендей шәкіртерді тәрбиелеуде физика пәнінің алатын орны бөлек.
Қазақстан Республикасының Президенті өз Жолдауында білім беру жүйесін жаңғырту барысында жүзеге асырылуға тиісті 6 түрлі міндетті алдымызға қойып отыр. Ол міндеттер мынадай: оқыту үдерісіне қазіргі заманғы әдістемелер мен инновациялық технологияларды кеңінен енгізу; педагогтар құрамының сапасын арттыру; біліктілікті бекітудің тәуелсіз жүйесін құру; жастарды әлеуметтік бейімделуге үйрету; оқыту үдерісінің тәрбиелік құрамдасын күшейту.
Қазақстан Республикасының «Білім туралы» жаңа Заңы дәл осы бәсеке- ге қабілетті отандық білім беру жүйесін қалыптастыруға бағытталған.
Жаңа заң туралы айтқанда оның құрылымына айрықша назар аударған жөн. Ол республикадағы жетілдірілген жаңа білім беру ортасын қалып- тастырудың концептуалдық идеясына сәйкес құрылған. Білім беру қызметі іштей жүйелендіріліп, оның барлық аспектілері құрылымға бағындырылған, қисындық сабақтастыққа сәйкес заңның мазмұнынан көрініс тапқан. Заң «білім беру жүйесі» ұғымы мен оны құрайтын білім беру деңгейлерінің анықтамасынан басталады. Одан әрі әр түрлі деңгейдегі оқу бағдарламалары арқылы білім берудің мазмұны ашылады. Келесі кезекте білім беруді ұйымдастыру, білім алушыларға қойылатын талаптар, қабылдау ережелері, оқу түрлері, білім берудің оқу, тәрбие, ғылыми және оқу-әдістемелік жұмыс сияқты түрлі бағыттары сипатталады.
Кезінде Ахмет Байтұрсынов айтқан екен: «оқытудың үш жағы бар, үшеуі үш нәрсеге тіреледі: біреуі оқу құралдарына, екіншісі ақша - қаражатқа, үшіншісі жақсы мұғалімге» деп. Егер осы айтылған үш мәселенің бірі біріне сай келіп жатса, оқыту үрдісінде қиындықтар болмас па еді? Мен өзім мұғалімдік мамандықта оқып жатқандықтан осы айтылған үш мәселенің екеуі мұғалімге қатысты айтылған деп есептеймін. Осы орайда мұғалімге тікелей қатысты мәселе - оқушылардың пәнге қызығушылығын ояту, ендеше буған қол жеткізетіндей жолдарды іздестіру керек.
Қазіргі оқыту процесіне жаңа педагогикалық технологиялар көптеп енуде. Оқушыны пәнге қызықтырумен қатар, саналы да салмақты ойлауға тәрбиелейтін, қоғамдық көзқарастарын қалыптастыра алатын, өзіндік пікірі бар, өмірдегі, қоғамдағы болып жатқан түрлі қарама-қайшылықтарды түсіне білетін, еркін сөйлеп, өз пікірін ашып айта алатын ойлы ұрпақ тәрбиелеуде білім мен ғылымның маңызы зор. Оқытудың әдіс-тәсілдерін түрлендіріп жетілдіру арқылы мектеп қабырғасында жүрген кезінде оқушылардың білім деңгейін, тәрбиесін жоғарлатып, таным деңгейін арттыру, пәнге қызықтыру әрбір мұғалімнің басты мақсаты болуы тиіс. Тиімді оқыту әдісі оқушыларды алғырлыққа, байқампаздыққа баулып, олардың ойлау қабілеттерінің жетілуі- не, ең бастысы, ғылым негізіне ынтасын арттыруға мүмкіндік туғызады.
Математиканы оқыту арқылы мәселені талдай білуге, нақтылауға, ұғымдарды анықтауға, ой қорытулар жасауға, дәлелдеуге тағы басқа іс - жүзінде қадам сайын логикалық білім беріледі. Математиканың өмірмен байланысы анық. Миды жаттықтыру үшін адамға математиканы үйрену, есеп шығару, математиканың бүкіл заңдарын басқа ғылымдарды оқығанда пайдаланады. Біздің өміріміздегінің бәрі бір - бірімен тығыз байланысты. Тіршілік құбылыстарын бір - бірінен бөліп зерттеуге болмайды.
Математиканың басқа ғылымдармен байланысын анықтайық. Оның химиямен, физикамен, биологиямен, информатикамен тығыз байлыныстылығында дау жоқ. Ал тарихпен ше? Тарих толығымен мерзімдер және оған сәйкес оқиғалардан тұрады. Оларды есте сақтау үшін ойлау қабілеті немесе оқиғалардың логикалық тізбегін қадағалай білу қажет. Географиямен байланысына келсек, қалалардың ара қашықтығын анықтағанда масштаб, қолда бар карталар есепке алынады, қарапайым математикалық есептеулер арқылы қажетті деректерді алуға болады.
Матемтиканы оқып - үйрену, есеп шығаруды үйрену үшін ғана емес, кез - келген проблеманы шеше білуге, өз қабілетіңді жетілдіру үшін де
қажет. Сондықтан, «Мен ақша санаймын, өз кірісім мен шығысымды есептей аламын, одан өзге математиканың маған қажеті шамалы» деуге болмайды. Егер олай десеңіз, адам өмірінің мәнін түсінбегеніңізді көрсетесіз, өмір деп отырғаныңыз шын мағынасында өмір емес, жай ғана тіршілік болады. Біз тек сол үшін жаратылған жоқпыз, бізге ақыл - ой сол үшін берілмеген. Біз өз өмірімізді мәнді қылып, барлық жетістіктерге жету үшін табиғаттағы барлық білімді пайдалана білуіміз керек.
Дипломдық жұмысымның зерттеу обьектісі: орта мектепте математика пәнін оқыту үрдісі.
Дипломдық жұмысымның орындалу мақсаты: Мәндес түрлендірулерді теңдеулер шешуде пайдаланып, оқытудың маңыздылығын көрсетіп, оқушыларға мәндес түрлендірулерді теңдеулер шешуде тиімді әдістерді үйлестіру арқылы оқыту әдістемесін ұсыну.
Дипломдық жұмыстың міндеттері:
- Мәндес түрлендірулерді теңдеулер шешуде пайдаланып, орта мектепте оқыту мәселесін зерделеу;
- Жалпы білім беретін мектептің жаратылыстану-математика бағытында «Тригонометриялық теңдеулерді шешу» тарауын оқытудың теориялық негізіндерін айқындау;
- «Квадрат теңдеулер» тарауын оқытуда оқушылардың танымдық әрекетіне негізделген тиімді әдістерді саралау;
- Математика курсының «Рационал теңдеу», «Тригонометриялық теңдеу», «Логарифмдік теңдеу» тарауларын оқыту әдістемесін жетілдіруге бағытталған ұсыныстар жасау.
Зерттеу әдістері: бақылау әдісі, салыстыру әдісі, оқу процесіне ену, талдау, тестілеу.
Дипломдық жұмыстың құрылымы:
Кіріспе, екі тарау, қорытынды, пайдаланылған әдебиеттер тізімі, қосымша.
Бірінші тарауда теңдеу ұғымы, теңдеу дегеніміз, теңдеу туралы жалпы мәліметтер мектеп курсында ашылып көрсетілген: теңдеу, теңдеу шешімдері; теңдеу шешудегі мәндес түрлендірулер; теңдеу шешудің әдістері.
Екінші тарау теңдеу шешуді, оқушыларды теңдеулер шешуде мәндес түрлендірулерді үйрету, «Тригонометриялық теңдеулер» тарауының оқыту әдістемесін жетілдіру жолдары көрсетілген: тақырыпқа қатысты тарихи материалдар; «Тригонометриялық теңдеулер» тарауын оқыту әдістемесі; жаңа оқыту технологиялардың кейбір түрлері және осы технологияларды пайдалана отырып, тригонометриялық теңдеулерді шешуде мәндес түрлендіре отырып, оқытуда оқушылардың қызығушылығын арттыру мәселесі; тарау тақырыптарына есептер шығару; тарауды компьютерде модельдеп оқыту әдістері.
Дипломдық жұмыстың нәтижелері Оңтүстік Қазақстан мемлекеттік педагогикалық институты студенттерінің ғылыми конференциясында және алдын-ала қорғау семинарында баяндалған.
1. Теңдеу туралы жалпы мәлімет
1. 1 Теңдеу. Теңдеудің шешімдері
Мектепте теңдеу мен теңсіздікті және олардың жүйелерін ерте бастан жүйелі түрде оқыту дәстүрі қалыптасты. Бұл дәстүр қазіргі бағдарламаларда да көрініс тапқан: теңдеу ұғымы, сызықтық теңдеу, екі белгісізі бар сызықтық теңдеулер жүйесі 6-сыныпта, квадрат теңдеулер мен рационал теңдеулер 7, 8-сыныпта, мәндес теңдеулер мен теңсіздіктер және тригонометриялық теңдеулер 10-сыныпта, дифференциалдық теңдеулер туралы ұғым, көрсеткіштік және логарифмдік теңдеулер 11-сыныпта оқытылады.
Теңдеу туралы теориялық мәліметтерді баяндау мектептегі алгебра курсының басқа тақырыптарын: нақты сандар, өрнектер мен функцияларды теңбе-тең түрлендіру, математикалық талдаудың бастамалары курсын өтудің мазмұны мен ретіне қарай жүргізіледі [1] .
Орта мектепте теңдеулер мен теңсіздіктерді олардың түрлеріне байланысты баяндаудың әртүрлі нұсқаулары кездеседі, кейде теңдеулер мен теңсіздіктерді параллель оқыту туралы ұсыныста бар.
Әдістемелік әдебиеттерде теңдеудің мынадай анықтамалары кездеседі.
- Екі алгебралық өрнекке енетін әріптің қандай да бір мәндерінде
бірдей сандық мәндер қабылдайтын теңдікті теңдеу деп атайды.
- Бір белгісізі бар теңдеу бойынша жазылады:Егерсаны
біріншіден
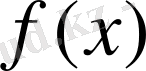 және
және
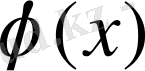 функцияларының анықталу облысына енетін болса, екіншіден мына сандық теңдік
функцияларының анықталу облысына енетін болса, екіншіден мына сандық теңдік
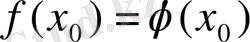 орындалатын болса, онда
орындалатын болса, онда
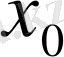 саны теңдеудің түбірі деп аталады. Теңдеуді шешу деп оның барлық түбірлерін табуды айтады.
саны теңдеудің түбірі деп аталады. Теңдеуді шешу деп оның барлық түбірлерін табуды айтады.
- Бір айнымалысы бар теңдеу деп осы айнымалы арқылы құрылған
теңдікті айтады. Теңдіктегі айнымалыны әдетте белгісіз шама деп атайды. Белгісіздің орнына апарып қойғанда берілген теңдеуді дұрыс теңдікке айналдыратын айнымалының мәнін теңдеудің түбірі (шешімі) деп атайды.
- Белгісізі бар теңдікті теңдеу деп атайды. Белгісіздің теңдікті дұрыс
сандық теңдікке айналдыратын мәндері теңдеудің түбірі деп аталады. Теңдеуді шешу дегеніміз оның барлық түбірлерін табу.
Теңдеу ұғымының бұл анықтамаларын бір-біріне қарсы қоюға болмайды. Бұл анықтамалардың әрқайсысы теңдеулерді шешудің теориялық және практикалық мәселелерінде қолданылады.
Мектеп оқулықтарында қазіргі кезде теңдеудің анықтамасы 4-анықтама негізінде алынған.
Теңдеу ұғымына ең жақын ұғым теңбе-теңдік. Бірақ ол көбінесе теңдеу ұғымына байланыссыз анықталады. Бұл әдетте теңбе-теңдік теңдеуден бұрын өтілген жағдайда кездеседі. Алдымен теңбе-теңдік айнымалының кез келген мәнінде дұрыс болатын теңдік деп қарастырылады. Кейінірек рационал бөлшектерді қарастырғанда теңбе-теңдік ұғымы дәлірек анықталады: айнымалының барлық мүмкін мәндерінде орындалатын теңдікті теңбе-теңдік деп атайды.
Теңдеу мен теңбе-теңдік ұғымдарының арасындағы тікелей байланыс мынадай анықтамамен беріледі: егер
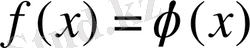 теңдеуінің шешімдерінің жиыны берілген теңдеудің анықталу облысымен сәйкес келетін болса, онда бұл теңдеуді теңбе-теңдік деп атайды [1, 2] .
теңдеуінің шешімдерінің жиыны берілген теңдеудің анықталу облысымен сәйкес келетін болса, онда бұл теңдеуді теңбе-теңдік деп атайды [1, 2] .
Сызықтық теңдеуді шешу бастауыш сынып математикасын оқытудан басталады.
- Бастауыш сыныптарда мынадай сызықтық теңдеуді шешу
қарастырылады:
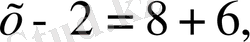
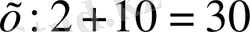 т. с. с. Белгісіз санды алдымен іріктеп, таңдап алу әдісін пайдаланып теңдеудің түбірі табылады. Кейін, теңдеудің түбірін табу арифметикалық амалдардың компоненттері мен нәтижелерінің арасындағы байланысқа сүйеніп табуға үйретіледі. Мысалы, бірінші теңдеуді шешкенде оқушылар былайша пайымдайды: «Белгісіз қосылғышты анықтау үшін қосындыдан белгілі қосылғышты алуымыз қажет:
т. с. с. Белгісіз санды алдымен іріктеп, таңдап алу әдісін пайдаланып теңдеудің түбірі табылады. Кейін, теңдеудің түбірін табу арифметикалық амалдардың компоненттері мен нәтижелерінің арасындағы байланысқа сүйеніп табуға үйретіледі. Мысалы, бірінші теңдеуді шешкенде оқушылар былайша пайымдайды: «Белгісіз қосылғышты анықтау үшін қосындыдан белгілі қосылғышты алуымыз қажет:
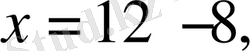
 ».
».
Теңдеулермен танысу формальді түрде жүргізілмейді. Мысалы, мынадай
есеп қарастырылады: «Белгісіз санға
 -ті қосқанда
-ті қосқанда
 шыққан. Белгісіз санды анықтаңдар». Есеп қысқаша түрде былай жазылады:
шыққан. Белгісіз санды анықтаңдар». Есеп қысқаша түрде былай жазылады:
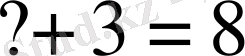 сымволының орнына қойылатын сан таңдап алу әдісімен анықталады. Бұдан кейін белгісіз санды
сымволының орнына қойылатын сан таңдап алу әдісімен анықталады. Бұдан кейін белгісіз санды
 арқылы белгілеп оны былайша жазуға болатындығы айтылады:
арқылы белгілеп оны былайша жазуға болатындығы айтылады:

- 5-сыныпта теңдеулер арифметикалық амалдардың компоненттері
мен нәтижелерінің арасындағы байланыс бойынша шешіледі, көбінесе алдын-ала өрнектерді ықшамдап алады. Мысалы,
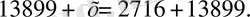 Оқушылар көбейтудің қосу (азайту) амалына қатысты үлестірілімдік заңын пайдаланып, мынадай
Оқушылар көбейтудің қосу (азайту) амалына қатысты үлестірілімдік заңын пайдаланып, мынадай
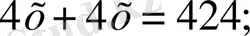
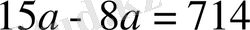 т. с. с. теңдеулерді шешеді. Ондық бөлшектерді өту кезінде мынадай теңдеулер шешіледі:
т. с. с. теңдеулерді шешеді. Ондық бөлшектерді өту кезінде мынадай теңдеулер шешіледі:
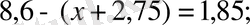
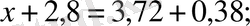
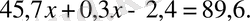
Бұл теңдеулерді шешу де арифметикалық амалдардың нәтижесі мен компоненттерінің қасиеттеріне негізделген [1, 3] .
- 6-сыныпта оң таңбалы және теріс таңбалы сандарды өткенде
сызықтық теңдеудің жаңа мысалдары, кейбір сызықтық емес теңдеулер қарастырылады. Қарама-қарсы сандардың анықтамасына сүйеніп, мынадай теңдеулердің
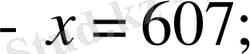
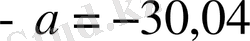 шешімдері анықталады. Модульдің анықтамасына сүйеніп
шешімдері анықталады. Модульдің анықтамасына сүйеніп
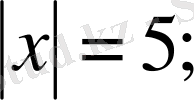
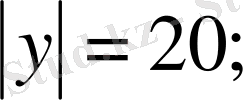
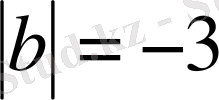 теңдеулерінің шешімдері табылады. 6-сыныпта «жақшаларды ашу» теңбе-тең түрлендіруімен танысқаннан кейін
теңдеулерінің шешімдері табылады. 6-сыныпта «жақшаларды ашу» теңбе-тең түрлендіруімен танысқаннан кейін
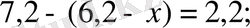
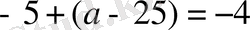 теңдеулерді шешудің жолы қысқартылады. Көбейтіндінің нольге тең болу шартын өткен соң мынадай теңдеулер шығарылады:
теңдеулерді шешудің жолы қысқартылады. Көбейтіндінің нольге тең болу шартын өткен соң мынадай теңдеулер шығарылады:
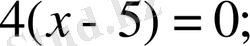
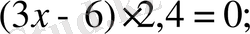
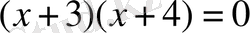 т. с. с. Оқушыларды теңдеулерді шешудің тәсілімен таныстырудың жаңа қадамы қосылғыштарды теңдеудің бір жағынан екінші жағына өткізу ережесі болып табылады. Осы ережеге сүйеніп, олар мынадай теңдеуді шешеді:
т. с. с. Оқушыларды теңдеулерді шешудің тәсілімен таныстырудың жаңа қадамы қосылғыштарды теңдеудің бір жағынан екінші жағына өткізу ережесі болып табылады. Осы ережеге сүйеніп, олар мынадай теңдеуді шешеді:
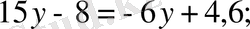
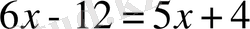 т. с. с.
т. с. с.
4. Одан кейін (6 сыныптың соңы немесе 7 сыныпта) сызықтық теңдеуді шешуге байланысты мәліметтер жүйеленеді. Кейбір оқу құралдарында бірінші дәрежелі теңдеу мен сызықтық теңдеудің айырмашылығы қарастырылады. Бірінші дәрежелі теңдеуің сызықтық теңдеудің дербес жағдайы екендігі айтылады.
Әдетте сызықтық теңдеу мына теңдікпен
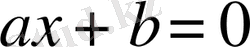 анықталады, мұндағы
анықталады, мұндағы
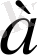 саны белгісіз алдында тұрған коэффицент деп, ал
саны белгісіз алдында тұрған коэффицент деп, ал
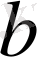 -бос мүше деп аталады.
-бос мүше деп аталады.
Бір белгісізі бар сызықтық теңдеуді шешудің жалпы тәсілін көрсеткен тиімді:

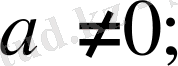
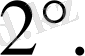
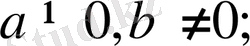
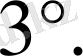
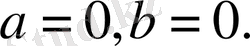
Оқушыларға бір теңдеуді шешудің бірнеше тәсілдерін табуға үйреткен пайдалы.
Мысалы,
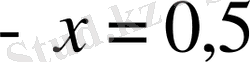 теңдеуін мынадай тәсілдермен шешуге болады:
теңдеуін мынадай тәсілдермен шешуге болады:
- алдымен бұл теңдеуді мына түрде жазып аламыз:одан кейін
белгілі айырма мен белгісіз азайғыштың арасындағы байланысқа сүйеніп, мынаны табамыз:
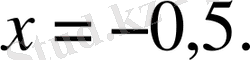
- қарама-қарсы сандардың анықтамасына сәйкес, белгісізсаны
санына қарама-қарсы. Сондықтан
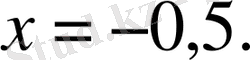
- мәндес теңдеулер туралы екінші теоремаға сүйенсек,
болады. Бұдан
Математиканы оқытудың психологиялық аспектілерінің бірі жаңа оқу
материалын өтудің себебін негіздеу болып табылады. Осы мәселені теңдеулердің жаңа түрін енгізу үшін қарастырайық. Математиканы оқыту әдістемесінде кері есеп ұғымды кездеседі. Бұл ұғымды түсіндірейік. Бір
 және
және
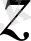 айнымалыларды туралы сөз болып, мұндағы
айнымалыларды туралы сөз болып, мұндағы
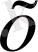 және
және
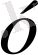 айнымалы шамалары берілген, ал
айнымалы шамалары берілген, ал
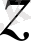 -ізделінді айнымалы шама. Енді мынадай есеп қарастырайық, мысалы
-ізделінді айнымалы шама. Енді мынадай есеп қарастырайық, мысалы
 және
және
 айнымалы шамалары берілген, ал
айнымалы шамалары берілген, ал
 - ізделінді айнымалы шама болсын. Есептің мазмұны мен айнымалы шамалардың арасындағы арақатыстар өзгермейтін болсын. Сонда мұндай екі есеп өзара кері есептер деп аталады. Өзара кері есептерді шешу үшін әртүрлі теңдеудің түрлері қолданылады. Сондықтан кері есептерді шешу мен құрастыру теңдеулердің жаңа түрін оқытуды негіздеудің пайдалы әдістемелік негізі болып табылады[1] .
- ізделінді айнымалы шама болсын. Есептің мазмұны мен айнымалы шамалардың арасындағы арақатыстар өзгермейтін болсын. Сонда мұндай екі есеп өзара кері есептер деп аталады. Өзара кері есептерді шешу үшін әртүрлі теңдеудің түрлері қолданылады. Сондықтан кері есептерді шешу мен құрастыру теңдеулердің жаңа түрін оқытуды негіздеудің пайдалы әдістемелік негізі болып табылады[1] .
Осындай есептерге мысалдар келтірейік.
- санына қандай да бір санды қосқандасанына кері сан
шыққан. Қандай сан қосылған?
- Қайсыбір оң санға-ті қосқанда, бірінші санға кері сан
шыққан. Осы сандарды табыңдар.
Бірінші есепті шешу мынадай сызықтық теңдеуге келтіріледі:
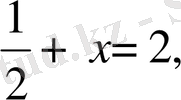 бұдан
бұдан
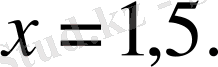 Екінші есептің шешуі
Екінші есептің шешуі
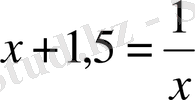 немесе
немесе
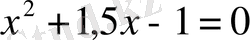 теңдеуіне келтіріледі. Сонымен, екінші есепті шығару үшін
теңдеуіне келтіріледі. Сонымен, екінші есепті шығару үшін
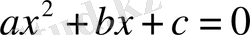 теңдеуді шеше білуі қажет.
теңдеуді шеше білуі қажет.
Теңдеулерді шешу әдісі көбейген сайын оқушыларда оларды
таңдап алу қиындығы туа бастайды. Осыған байланысты теңдеуді шешудің тәсілдерін анықтауға арнаулы тапсырмалар қарастырған пайдалы. Мұндай тапсырмаларды орындауды екі кезеңмен жүргізген тиімді:
- алдымен берілген теңдеулер үшін тек шешу жолдарын ғана көрсету;
- одан соң теңдеулерді шешу.
Теңдеулер мен теңсіздіктер оқулықта әртүрлі баяндалады. Біз
төменде Т. А. Алдамұратованың «Математика-6» оқулығындағы «Теңдеу» тақырыбының баяндалуын қарастырайық.
Құрамында әріппен белгіленген белгісізі (айнымалысы) бар
теңдік теңдеу деп аталады. Мысалы,
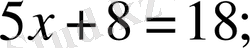
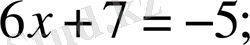
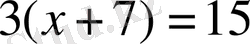 теңдеулер,
теңдеулер,
 -белгісіз (айнымалы) . Мұндай теңдеулерді бір белгісізі бар немесе бір айнымалысы бар теңдеулер деп атайды.
-белгісіз (айнымалы) . Мұндай теңдеулерді бір белгісізі бар немесе бір айнымалысы бар теңдеулер деп атайды.
Теңдеулердің оң жағы және сол жағы болады. Мысалы,
 теңдеудегі
теңдеудегі
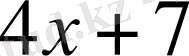 - теңдеудің сол жағы, ал
- теңдеудің сол жағы, ал
 -теңдеудің оң жағы. Теңдеудегі алгебралық қосылғыштардың әрқайсысы оның мүшелері деп аталады
-теңдеудің оң жағы. Теңдеудегі алгебралық қосылғыштардың әрқайсысы оның мүшелері деп аталады
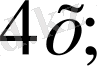
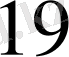 -мүшелер. Мұндағы
-мүшелер. Мұндағы
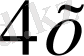 -белгісізі бар мүше,
-белгісізі бар мүше,
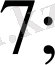
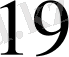 -бос мүшелер.
-бос мүшелер.
Теңдеумен берілген мысалдар мен есептерді шығарғанда,
ондағы әріппен берілген белгісіздің немесе айнымалының сан мәнін табамыз.
Белгісіз санның немесе айнымалының теңдеуді дұрыс санды
теңдікке айналдыратын мәні теңдеудің түбірі деп аталады.
Теңдеуді шешу дегеніміз - оның түбірлерін табу немесе түбірлерінің жоқ екенін дәлелдеу. Теңдеулерді шешкенде кейде түбірлері бірдей болатын теңдеулер де кездеседі. Түбірлері бірдей болатын теңдеулерді мәндес теңдеулер деп атаймыз. Мысалы,
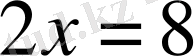 теңдеуімен
теңдеуімен
 және
және
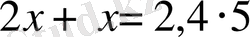 теңдеулері мәндес теңдеулер. Түбірлері бірдей:
теңдеулері мәндес теңдеулер. Түбірлері бірдей:
 Ескеретін жағдай, кейде теңдеудің түбірі болмайды. Түбірлері болмайтын теңдеулер де мәндес теңдеулер болып саналады [1, 2, 3] .
Ескеретін жағдай, кейде теңдеудің түбірі болмайды. Түбірлері болмайтын теңдеулер де мәндес теңдеулер болып саналады [1, 2, 3] .
Теңдеулерді мәндес түрлендіргенде мынадай қасиеттер пайдаланылады.
- Теңдеуді екі жағына да бірдей санды немесе әріпті өрнекті қосқанда
(азайтқанда) теңдеу мәндес теңдеуге түрленеді.
- Теңдеудегі қосылғыштардың таңбасын қарама-қарсыға өзгертіп, оны
теңдеудің бір жағынан екінші жағына көшіргенде теңдеу мәндес теңдеуге түрленеді.
- Теңдеудің екі жағын да нөлден өзге бірдей санға көбейткенде немесе
бөлгенде теңдеу мәндес теңдеуге түрленеді.
Бір айнымалысы бар екі өрнектің теңдігін ықшамдап,
түріне
келтіріледі.
- Егерболса, теңдеудің бір ғанатүбірі болады.
Мысалы:
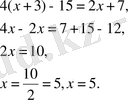
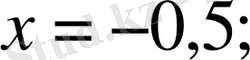
- Егерболсатеңдігі-тің ешбір мәнінде дұрыс теңдік
болмайтындықтан, теңдеудің түбірі болмайды.
Мысалы:
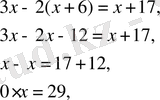
бұл теңдеудің түбірі болмайды.
- Егерболсатеңдігі-тің кез келген мәнінде дұрыс
санды теңдік, сондықтан бұл жағдайда теңдеудің шексіз көп түбірі болады.
Мысалы:
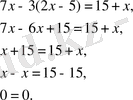
Теңдеудің түбірі - кез келген сан.
1. 2 Теңдеу шешудегі мәндес түрлендірулер
Теңдеулерді шешу кезінде әр түрлі түрлендірулер жүргізіп, алдыңғымен салыстырғанда қарапайым түрге келтіреді. Түрлендірулер тізбегі нәтижесінде пайда болған, соңғы теңдеудің шешімдері берілген теңдеудің түбірлері бола ма, бөгде түбірлер қайдан пайда болды немесе теңдеудің түбірлеінің жоғалып кету жағдайлары неліктен орын алды деген мәселелер мәндес теңдеулер ұғымымен байланысты. Қандай теңдеулер мәндес деп аталынады, қандай түрлендірулер мәндес түрлендірулер болады, қандай жағдайда мәндес емес, оны қалай білуге болады, т. б. мәселелерді оқушылар саналы түрде меңгеруі керек.
Мектеп математика курсында мәндес түрлендіру ұғымы біртіндеп, оқушыларда ол ұғымға деген қажеттілік пайда болып, белгілі бір тәжірибе жинақталғанда енгізіледі. Математика тілінде қандай да бір терминнің пайда болуы, оған деген қажеттілік болғанда ғана енгізілетінін оқушы түсінуі тиіс.
Сызықтық теңдеулер мен квадрат теңдеулерді оқып үйрену кезінде мәндес теңдеу және мәндес түрлендіру туралы мәселе келтірілмейді. Себебі бұл жерде мәндес емес түрлендіру мүлде болмайды, сондықтан мәндес теңдеу терминін енгізуге деген қажеттілік те жоқ.
Алгебралық бөлшектерді оқып үйренуге байланысты, бөлшек рационал теңдеулердің бөлімінен құтылу кезінде бөгде түбірлердің пайда болуы туралы алғашқы түсінік беріледі. Сол кезде бірінші рет мәндес теңдеу термині енгізіледі. Осы кезде мәндес теңдеу ұғымын енгізуге деген қажеттілік те пайда болады, тәжірибеде жинақталады[1] .
Түбірлері бірдей болатын екі теңдеуді өзара мәндес теңдеулер деп атайды. Бір теңдеудің әрбір түбірі екінші теңдеуді де қанағаттандырса және керісінше, екінші теңдеудің кез келген түбірі бірінші теңдеуді қанағаттандырса, онда олар мәндес немесе эквивалент теңдеулер делінеді. Дербес жағдайда, түбірлері жоқ барлық теңдеулер өзара мәндес. Мысалы, мына теңдеулер мәндес:
 және
және
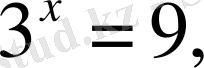
 және
және
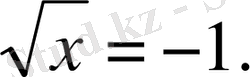
Егер
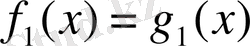 теңдеуінің әрбір түбірі бір уақытта
теңдеуінің әрбір түбірі бір уақытта
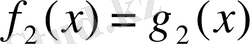 теңдеуінің де түбірлері болса, онда
теңдеуінің де түбірлері болса, онда
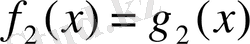 теңдеуі
теңдеуі
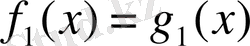 теңдеуінің салдары деп, немесе теңдеу-салдар деп аталады.
теңдеуінің салдары деп, немесе теңдеу-салдар деп аталады.
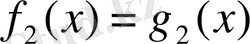 теңдеуі
теңдеуі
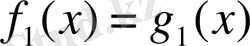 теңдеуінің салдары екендігін көрсету үшін,
теңдеуінің салдары екендігін көрсету үшін,
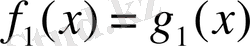 теңдеуін қанағаттандыратын х-тің барлық мәндері
теңдеуін қанағаттандыратын х-тің барлық мәндері
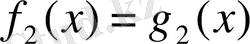 теңдеуін көз жеткізу жеткілікті.
теңдеуін көз жеткізу жеткілікті.
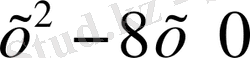 теңдеуінің салдары
теңдеуінің салдары
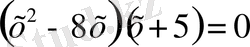 теңдеуі болатындығын көрсету үшін
теңдеуі болатындығын көрсету үшін
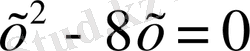 теңдеуінің әрбір түбірі
теңдеуінің әрбір түбірі
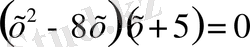 теңдеуінің де шешімі болатындығына көз жеткізіледі.
теңдеуінің де шешімі болатындығына көз жеткізіледі.
Егер екі теңдеудің бірі екіншісінің салдары және керісінше болса, онда екі теңдеу мәндес болады.
Қандай жағдайда бір теңдеуден екінші теңдеуге өткенде мәндес түрлендіру болады деген мәселеге тоқталайық.
Төмендегідей үш теорема орындалатындай түрлендіру жасағанда бір теңдеуден екінші теңдеуге өту әр уақытта мәндес түрлендіру болады.
1-теорема. Егер теңдеудің қандай да бір мүшесін кері таңбамен теңдіктің бір жағынан екінші жағына шығарса, онда пайда болған теңдеу берілген теңдеумен мәндес болады [1, 20] .
2-теорема. Егер теңдеудің екі жағын да бірдей тақ көрсеткішті дәрежеге шығарсақ, онда пайда болған теңдеу берілген теңдеумен мәндес болады.
3-теорема.
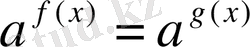 (мұндағы
(мұндағы
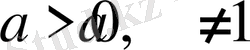 ) теңдеуі
) теңдеуі
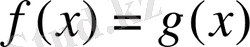 теңдеуімен мәндес.
теңдеуімен мәндес.
Бұл теоремаларды қолданғанда бөгде түбір пайда болмайды, түбірлердің жоғалып кетуі де мүмкін емес.
Ал мына төмендегі теоремалар белгілі бір шарттар орындалғанда ғана жұмыс істейді, яғни оларды қолдану кезінде ұқыптылықты қажет етеді.
4-теорема. Егер
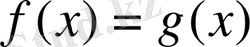 теңдеуінің екі жағын да бірдей, берілген теңдеудің анықталу облысының барлық жерінде мағынасы бар, осы облыстың ешбір жерінде нөлге айналмайтын
теңдеуінің екі жағын да бірдей, берілген теңдеудің анықталу облысының барлық жерінде мағынасы бар, осы облыстың ешбір жерінде нөлге айналмайтын
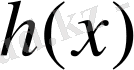 өрнегіне көбейтсе, онда берілген теңдеуге мәндес
өрнегіне көбейтсе, онда берілген теңдеуге мәндес
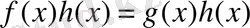 теңдеуі пайда болады.
теңдеуі пайда болады.
Бұл теоремамен жұмыс істегенде теңдіктің екі жағына да көбейтілетін
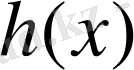 өрнегінің:
өрнегінің:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz