Анықталған интеграл: анықтамасы, геометриялық мағынасы және негізгі қасиеттері


Анықталған интеграл ұғымына келтірілген есептер
Интегралдық есептеу, дифференциалдық есептеуден тәуелсіз, одан бұрын дамыған ілім. Осы екі ілімнің арасындағы терең байланыс тек ХVІІ ғасырдың аяғында ғана тағайындалды. Бұл екі ілімнің шешетін негізгі проблемалары шексіз аздар немесе математикалық анализдің өзара кері проблемалары болды; қосу мен азайту амалдары бір-бірімен қандай қатынаста болса, функцияларды интегралдау және дифференциалдау амалдары да бір-бірімен сондай қатынаста болады. Осы тарихи кез қазіргі уақыттағы «Математикалық анализ» деп аталатын ілімнің туу кезі. Сол кезден бастап математика ғылымының осы екі тарауы тез дами бастады; әсіресе интегралдық есептеу жеке бытыраңқы есептерді шешуден, өте әлді жалпы методтар жасауға көшті.
Шынында, анықталған интеграл ұғымы геометрия, механика және физика проблемаларын шешудің нәтижесінде туған.
Анықталған интегралдың математикалық анықтамасын берместен бұрын оған келтірілетін есептерді қарастырайық.
1. Мынадай геометриялық есепті қарайық: у=f(x), [a, b] аралығында берілген үздіксіз және осы аралықта үдеме функция болсын. ОХ осімен жоғары жатқан АМВ доғасы осы функциямен кескінделетін болсын, былайша айтқанда, y=f(x) АМВ қисығының теңдеуі.
Жоғарғы жағынан АМВ доғасымен, бүйір жағынан АР және BQ ординаталарымен, төменгі жағынан PQ кесіндісімен қоршалған жазық фигураның ауданын табу керек.
Бұл есепті шешу үшін, [a, b] аралығын немесе PQ кесіндісін абсциссалары мына сандарға тең a=x 0 , x 1 , x 2 , …, x n-1 , x n =b аралық нүктелермен n бөлшек кесінділерге бөлеміз, сонан соң осы бөлу нүктелері арқылы ОУ осіне доғамен қиылысқанша параллельдер жүргіземіз. Сонда есептеп табайық деп отырған ауданымыз п қисық сызықты трапецияларға жіктелінеді.
Енді ұсақ трапециялардың ішінен і-ші трапецияны сайлап алайық, бұл трапецияның бір бүйір қабырғасы [x 1 , x i+1 ] бөлшек аралықтың ұзындығына, яғни мына санға тең: x i+1 - x i екінші бүйір қабырғасы қисық доға.
Табаны [x 1 , x i+1 ] бөлшек аралықта жататын, биіктіктері f(x i ) f(x i+1 ) сандарына тең тік төртбұрышты құрайық. Сонда жаңағы сайлап алған трапецияның ауданы мына екі санның: f(x i ) (x i+1 - x i ) және f(x i+1 ) (x i+1 - x i ) арасында жатады. Егер көрсетілген осы тік төртбұрыштарды барлық бөлшек сегменттерде құрсақ және ол тік төртбұрыштардың аудандарын s және S арқылы белгілесек, сонда
n-1
S=f(x 0 ) (x 1 - x 0 ) + f(x 1 ) (x 2 - x 1 ) +… f(x n-1 ) (x n - x n-1 ) =∑ f(x 1 ) (x i+1 - x 1 )
i=0
n-1
S=f(x 1 ) (x 1 - x 0 ) + f(x 2 ) (x 2 - x 1 ) +… f(x n ) (x n - x n-1 ) =∑f(x i+1 ) (x i+1 - x i )
i=0
егер іздеп отырған ауданның шамасын u деп белгілесек, онда бұл аудан төмендегі теңсіздікті
s<u<S
қанағаттандырады.
Енді S пен s-тің айырмасын құрайық:
S-s=(x 1 -a) [f(x 1 ) -f(a) ] +(x 2 +x 1 ) [f(x 2 ) -f(x 1 ) ] +…+(b-x n-1 ) [f(b) -f(x n-1 ) ] (1)
X 1 -a, x 2 -x 1 , …, b-x n-1 айырмалардың ішіндегі ең үлкені η болсын, егер барлық осы айырмалардың орнына η санын қойсақ, онда (1) теңдіктің оң жағы өскен болар еді, яғни
S-s<η[f(x 1 ) -f(a) +f(x 2 ) -f(x 1 ) +…+f(b) -f(x n-1 ) немесе S-s<η[f(b) -f(a) ] .
Кейінгі теңсіздіктен біз мынадай қортындыға келеміз: барлық x i+1 -х і айырмалардың ең үлкені нольге ұмтылғанда, айырма S-s та нольге ұмтылады және мұнымен бірге мына айырмалар да S-u, u-s нольге ұмтылады, олай болса u осы ек S және s қосындылардың ортақ шегі. Сонымен,
n-1 n-1
u= lim ∑ f(x i ) (x i+1 - x i ) =lim ∑ f(x i+1 ) (x i+1 - x i )
η→0 i=0 η→0 i=0
Сөйтіп, іздеп отырған ауданның шамасы барлық бөлшек сегментетрдің ұзындықтары нольге ұмтылғандағы S пен s-тің шегіне тең болатын болды.
Айтылып отырған қортынды кеміне функция үшін де дұрыс. Егер f(x) функцияның [a, b] аралығында бірнеше максимум және минимум болса, онда [a, b] аралығын функцияның не максимумы, не минимумы болғандай етіп бірнеше бөлшек аралықтарға (сегменттерге) бөлеміз.
Барлық бөлшек сегментерді табандары есебіне алып жоғарыда айтылғандай тік төртбұрыштарды құрамыз. Мұндай тік төртбұрыштардың саны n. Осы тік төртбұрыштардың ішінен біреуін, мәселен, к-інші тік төртбұрышты сайлап алайық. Бұл сайлап алған тік төртбұрыштың ауданы мынаған тең:
[a(1+α) k -a(1+a) k-1 ] Aa μ (1+a) (k-1) μ =Aa μ+1 a(1+a) (k-1) (μ+1)
Олай болса, құрылған барлық тік төртбұрыштардың аудандарының қосындысы болады:
S=A μ+1 a[1+(1+a) μ+1 +(1+a) 2(μ+1) +…+(1+a) (n-1) (μ+1) ] (2)
Егер μ+1 саны нольге тең болмаса, онда (2) теңдікті оң жағындағы квадрат жақшалардың ішіндегі өрнек еселігі мына санға (1+а) μ+1 тең, геометриялық прогрессияның қосындысы, сондықтан
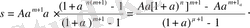
Егер кейінгі формуладағы а(1+а) n орына b санын қойсақ, онда
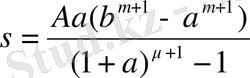
(3)
Енді іздеп отырған ауданның шамасын табу үшін, а-ны нольге ұмтылып (3) тедіктің шегін табамыз. Сонымен, ізделініп отырған ауданның шамасын u деп белгілесек, онда

Егер μ=-1 болса, онда бағанағы іштей қоршалған тік төртбұрыштың аудандарының қосындысы (2) теңдік бойынша тең болады; S=n A a, міне, осы өрнектің шегін табу керек; мұнда n мен а төмендегі қатыс
a(1+a) n =b (4)
арқылы бір-бірімен байланысты.
(4) теңдіктің екі жағын а санына бөліп жіберіп, сонан кейін логарифм дейміз. Сонда
nln(1+a) =ln
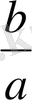
немесе бұл арадан
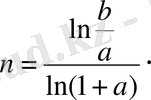
Кейінгі теңдіктің екі жағын Аа -ға көбейтеміз де, а-ны нольге ұмтылып шек аламыз, сонда

а→0 а→0 а→0 а→0
сонымен, бұл жағдайда ізделініп отырған аудан
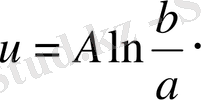
Интегралдық есептеудің тууының өзі фигуралардың аудандарын есептеп табудың нәтижесінде пайда болғаны мәлім. Айталық функция у=f(x), XOY жазықтығында үздіксіз бір қисық сызықты кескінделсін. Онда біз мына теңдеуді у=f(x) осы қисықтың теңдеуі деп айтамыз. Енді біз осы қисықпен, ОХ осімен, қозғалмайтын М 0 Р 0 ординатамен және айналымы МР ординатамен қоршалған ауданды қарастырайық, бұл ауданның шамасын u деп белгілейік. Осы айтылып отырған ауданның шамасы сөзсіз МР-нің абсциссасына тәуелді болады. функция f(x) үздіксіз болғандықтан, аудан u(х) те үздіксіз болады.
Бір-біріне өте жақын жатқан екі МР және NQ ординаталарды қарастырайық. Бұл ординаталардың абсциссалары болады х және х+∆х. PQ=∆х кесіндісін табаны үшін алып, тік төртбұрыштарды құрайық. Бұл тік төртбұрыштардың біреуінің биіктігі MN доғаның ең үлкен ординатасына, екіншісінің биіктігі жаңағы доғаның ең кіші ординатасына тең болсын. Ең үлкен ординатны Н арқылы, ең кіші ординатаны Һ арқылы белгілейік.
Ауданы u(х) -тің есімшесі ∆u жоғарыда айтылған тік төртбұрыштардың аудандарының арасында жатады, яғни
Һ∆х < ∆u <Н∆х
немесе ∆х-ке бөліп мына табамыз:
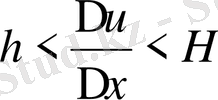
Бұл теорема-интегралдық есептеудің негізгі теоремасы. Негізгі теореманы геометриялық интуицияға (сезімге) сүйеніп отырып дәлелдедік. Бұлай дәлелдеу дұрыс болғанымен, логикалық жағынан жеткілікті дәлелдеу болып табылмайды. Көп уақыт бойы ғылыми жұртшылық ослыай дәлелдеуге риза болып келді.
Интегралдық есептеуді мызғымас негізге келтіру үшін бұл теореманы, геометриялық елеске көшпей, аналитикалық жолмен дәлелдеу қажет.
Анықталған интеграл ұғымына тек геометриялық есептер ғана келтіріп қоймайды, физикалық есептер де келтіреді. Мысал үшін, төмендегі физикалық есепті қарайық. Материалды нүкте р күшінің әрекетімен түзу сызықтың бойымен қозғалады деп ұйғарайық. Күштің бағыты қозғалыс бағытымен дәл келсін де, жүрілген жолдың ұзындығы l болсын.
Егер күш р тұрақты болса, онда бұл күштің өндірілген жұмысының шамасы pl болады. ал егер күш р айнымалы болса, онда жаңағы жазылған көбейтіндіні қоданып, күштің өндірген жұмысын табуға болмайды, басқа жолды қоддануға тура келеді. Міне, енді біз осыған келейік.
Материалды нүкте М айнымалы р күшінің әсерімен түзудың бойымен қозғалсын. Осы түзуді абсцисса осі үшін алайық. Нүктеге әсер етуші күштің шамасы оның жағдайына тәуелді болсын, былайша айтқанда, М нүктесінің абсциссасы х-тің функциясы болсын:
р=f(x)
р күшінің әсерімен М нүктесі х 0 =aжағдайдан х n =b жағдайда келетін болсын. Енді осы күштің [a, b] аралығында өндіретін жұмысын есептеп табайық. Ол үшін[a, b] аралығын бірдей етеп n бөлшек сегментерге бөлеміз. Бөлуші нүктелер мына тәртіппен орналассын:
a=x 0 <x 1 < x 2 <…<x n-1 <x n =b
Анықталған интегралдың аналитикалық анықтамасы
Геометриялық интуцияға сүйенсек, шама және сан ұғымы арқылы анықталған интегралды анықтау тек өткен ғасырда ғана шешілді. Мұндай анықтаманы ресми немесе аналитикалық анықтама дейді, міне, осы анықтамаға келейік.
у=f(x), [a, b] аралығында анықталған, бұл аралықтың ешбір нүктесінде шексіздікке айналып кетпейтін, басқаша айтқанда, шектелген функция болсын. Бұл функция үздіксіз және үзілісті болуы да мүмкін.
Анықталған интегралдың геометриялық мағнасына тоқтап кетейік. Ең әуелі (a, b) аралығында функция f(x) оң деп ұйғарайық. у=f(x) теңдеумен берілген қисықпен, абсцисса осыімен және ордината осіне параллель x=a, x=b түзулермен қоршалған фигураның ауданын қарайық.
Интегралдық қосындының әрбір қосылғышы ƒ(ξі) ∆х і табаны ∆х і -ге, биіктігі ƒ(ξі) -ге тең тік төртбұрыштың ауданын береді; олай болса, интегралдық қосындының өзі, барлық бөлшек сегменттер [x i , x i+1 ] (i=0, 1, 2…, n-1) табаны есебінде алынып құрылған, биіктіктері ƒ(ξ і ) (і=0, 1, 2, …, n-1) сандарына тең тік төртбұрыштардың (тікшелердің) аудандарының қосындысын береді.
Сондықтан барлық бөлшек сегменттердің ұзындықтарының ең үлкені нольге ұмтылғандағы интегралдық қосындының шегі жоғарыдағы айтылған жазық фигураның ауданын өрнектейді.
Анықталған интегралдың геометриялық мағынасы: y=f(x) теңдеумен берілген қисықпен, ОХ осімен ОУ осіне параллель x=a, x=b түзулермен қоршалған облыстың ауданы болатын болды.
Егер функция f(x), [a, b] аралығында нольден кем, яғни теріс таңбалы болса немесе бұл аралықта оның таңбасы өзгеріп тұратын болса да, бәрібір кейінгі тұжырымдалған қортынды дұрыс болады. бірақ мұнда бір айтып кететін мәселе мынау: егер функция f(x) -тің таңбасы [a, b] кесіндінің барлық нүктелерінде теріс болса, онда функцияны кескіндейтін қисықтың АВ доғасы ОУ осінің теріс жағында жатқан болар еді және ƒ(ξ і ) ∆х і <0, өйткені ƒ(ξ і ) <0, ∆х і =x i+1 -х і >0. Олай болса, интегралдық қосындының таңбасы теріс болады, демек, мына өрнек:
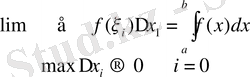
Егер [a, b] кесіндісінде f(x) функцияның таңбасы бірнеше рет өзгерсе, былайша айтқанда, бұл функцияның графигі Х-тер осін бірнеше қиса, онда анықталған интеграл
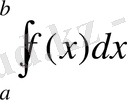 абсцисса осі мен қисықтың және x=a, x=b ординаталардың арасында жатқан облыстардың аудандарының алгебралық қосындысына тең болады.
абсцисса осі мен қисықтың және x=a, x=b ординаталардың арасында жатқан облыстардың аудандарының алгебралық қосындысына тең болады.
Анықталған интегралдың қасиеттері
Егерфункция f(x) [a, b] аралығында интегралданатын болса, онда ол [a, b] аралығында да интегралданады және
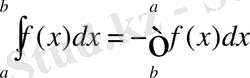
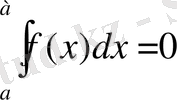 Анықтама бойынша
Анықтама бойынша
Функция f(x) мына үш [a, b], [a, c] және [c, b] аралықтардың ең үлкенінде интегралданатын болсын; онда бұл функция қалған аралықтардың екеуінде де интегралданатын болады.
Дәлелдеу. с нүктесі а мен b-нің арасында жататын, болсын, яғни a<c<b, f(x) [a, b] аралығында интегралданатын функция. Олай болса, бұл функция [a, c] [c, b] аралықтарында интегралданатынын біз жоғарыда айтап кеттік.
[a, b] аралығын бөлшек сигменттерге бөлеміз және с нүктесін бөлу нүктесінің бірі деп есептейміз де, интегралдық қосындыны құрамыз, сонда
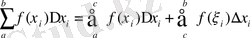
енді мах ∆х і -ді нольге ұмтылтып, кейінгі теңдіктің екі жағынан шек аламыз, сонда
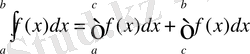
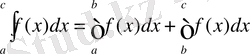 Енді с нүктесі [a, b] аралығының сыртында жатқан жағдайды қарастырайық. Соынмен, a<b<c болсын, онда формула бойынша
Енді с нүктесі [a, b] аралығының сыртында жатқан жағдайды қарастырайық. Соынмен, a<b<c болсын, онда формула бойынша
немесе бұл арадан
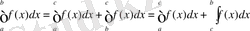
сонымен, формула с нүктесі [a, b] аралығы жөнінде қалай орналасса да дұрыс болатын болды.
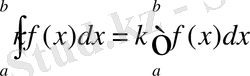 Егер функция f(x) [a, b] аралығында интегралданатын болса, онда κ f(x) (мұнда к-тұрақты сан) да осы аралықта интегралданатын болады және
Егер функция f(x) [a, b] аралығында интегралданатын болса, онда κ f(x) (мұнда к-тұрақты сан) да осы аралықта интегралданатын болады және
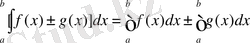 Егер екі функция f(x) және g(x) [a, b] аралығында интегралданатын болса, онда f(x) ±g(x) интегралданатын болады және
Егер екі функция f(x) және g(x) [a, b] аралығында интегралданатын болса, онда f(x) ±g(x) интегралданатын болады және
Бұл қасиеттерді оқушылардың өздері де дәлелдей алады.
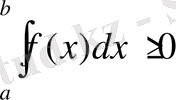 Егер [a, b] аралығында интегралданатын функция f(x) теріс болмаса және a<b, онда
Егер [a, b] аралығында интегралданатын функция f(x) теріс болмаса және a<b, онда
Мұны да оқушылардың өздері дәделдей алады.
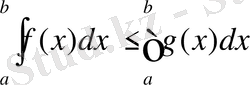 [a, b] аралығында интегралданатын функциялар f(x) және g(x) осы аралықтың барлық нүктелері үшін мына теңсіздікті қанағаттандырса, f(x) ≤g(x) немесе f(x) <g(x), онда
[a, b] аралығында интегралданатын функциялар f(x) және g(x) осы аралықтың барлық нүктелері үшін мына теңсіздікті қанағаттандырса, f(x) ≤g(x) немесе f(x) <g(x), онда
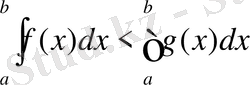
немесе
Осының алдындағы қасиет бойынша
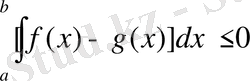
бұл арадан дәлелдейік деп отырған теңсіздік келіп шығады.
Егер функция f(x) [a, b] аралығында интегралданатын болса және a<b болса, онда
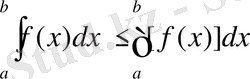
Егер функция f(x) [a, b] аралығында интегралданатын болса, онда f(x) да осы аралықта интегралданатынын біз жоғарыда дәлелденген болатынбыз.
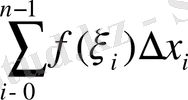 Енді теңсіздіктің дұрыстығын дәледейік. Ол үшін [a, b] аралығын n бөлшек сигменттерге бөліп, интегралдық қосындысын құрамыз:
Енді теңсіздіктің дұрыстығын дәледейік. Ол үшін [a, b] аралығын n бөлшек сигменттерге бөліп, интегралдық қосындысын құрамыз:
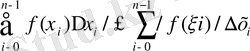
ал
мах ∆х і -ді нольге ұмтылып, теңсіздіктің екі жағынан шек аламыз, сонда
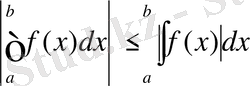
болады.
Егер функция f(x) [a, b] аралығында интегралданатын болса және осы аралықтың барлық нүктелері үшін төмендегі қос теңсіздік
m≤f(x) ≤M
орындалса, онда
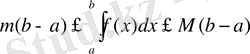
мына теңсіздіктердің
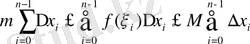
орындалуы өзінен-өзі айқын. Осы арадан шекке көшсек, дәлелдейік деп отырған теңсіздіктер келіп шығады.
Егер функция f(x) (a, b) аралығында интегралданатын болса және осы аралықтың барлық нүктелері үшін мына теңсіздіктер
m≤f(x) ≤M
орындалса, онда
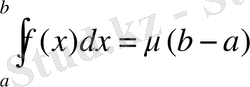
мұнда μ, m мен М -нің арасында жатқан сан:m≤μ≤M.
Қасиет бойынша
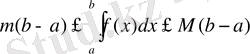
бұл арадан
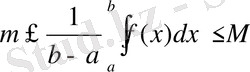
былай ұйғарып
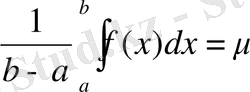
керекті теңдікті дәлелдейміз.
Қасиеттен мына салдар келіп шығады: егер функция f(x) [a, b] аралығында үздіксіз болса, онда теңдіктің орнына төмендегі теңдік болады:
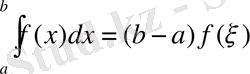
мұнда ξ-а мен b-нің арасында жатқан тиянақты бір сан.
Теңдіктің дұрыстығын былайц дәлелдейміз: функция f(x) [a, b] аралығында үздіксіз болғандықтан, Вейерштрасс теоремасы бойынша ол өзінің дәл төменгі m және дәл жоғарғы М шекаралықтарын қабылдайды. Олай болса, Коши теоремасы бойынша функция f(x) m мен М-нің арасында жатқан барлық сандарды қабылдайды, былайша айтқанда, [a, b] аралығында ең болмағанда бір ξ нүктесі табылып, осы нүктедегі f(x) функциясының мәні μ санына тең болады, яғни μ=f(ξ) .
Қасиетті және оның салдарын, анықталған интегралдың орта мәні жөніндегі теорема деп атайды. Енді формуланың геометриялық мағынасына көшейік. Бұл теңдіктің сол жағындағы анықталған интеграл функцияның графигімен, абсцисса осімен, x=a және x=b түзулермен қоршалған фируганың ауданын береді, ал оның оң жағында тұрған көбейтінді биіктігі f(ξ) -ге табаны b-a -ға тең тік төртбұрыштың ауданын кескіндейді.
Анықталған интегралдың орта мәні жөніндегі жоғарыда тұжырымдалған теореманы жалпылауға болады.
f(х) және g(x) [a, b] аралығында интегралданатын функциялар болсын, [a, b] аралығында жатқан барлық нүктелер үшін функция (х) мына теңсіздікті m≤f(x) ≤M қанағаттандырсын да, ал g(x) таңбасын өзгертпесін: g(x) ≥0 [g(x) ≤0], сонда
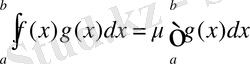
мұнда μ-m мен М-нің арасында жатқан сан.
Дәделдеу. Ең әуелі g(x) ≥0 болсын деп ұйғарайық.
Онда
Mg (x) ≤ f(x) g (x) ≤Mg (x)
Бұл теңсіздіктердің барлық жағын интегралдап, мынаны табамыз:
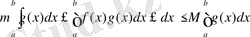
Қасиет және g(x) функция туралы ұйғару бойынша
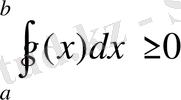 Сондықтан кейінгі тесіздіктердің әрбір жанын
Сондықтан кейінгі тесіздіктердің әрбір жанын
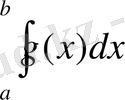 -ке бөліп жіберіп табамыз:
-ке бөліп жіберіп табамыз:
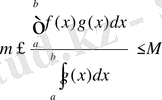
Былай ұйғарып,
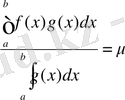
керекті нәтиежеге келеміз.
Бұл теоремадан да мынадай салдар шығады: егер функция f(x) [a, b] аралығында үздіксіз болса, онда формуланың орнына мына формула қолданылады:
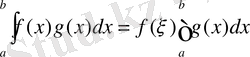
Мұнда ξ-a мен b-нің арасында жатқан бір тиянақты сан.
Егер функция f(x) [a, b] аралығында интегралданатын болса, онда ол [a, x] аралығында да интегралданатынын (мұнда x-a мен b-нің арасында жатқан кез келген мәнді көрсетеді) біз жоғарыда көрсеттік. Анықталған интегралдың жоғарғы шегі b-ні х-пен ауыстырып, мына өрнекті табамыз:
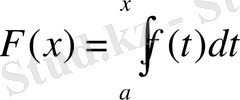
Әрине, бұл өрнек, х-тің функциясы болып табылады. Енді осы функцияға қандай қасиеттер тән, соны зерттейік.
Егер функция f(x) [a, b] аралығында интегралданатын болса, онда Ғ(х) осы аралықта х-тің үздліксіз функциясы болады.
Дәделдеу. х-ке еркімізше ∆х=Һ өсімшені берейік. Нүкте х+Һ қарастырып отырған аралықтың сыртына шығып кетпеуі керек. Сонда
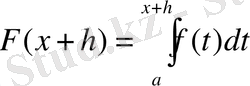
Бұл арадан
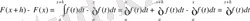
кейінгі теңдіктің оң жағында тұрған интегралға анықталған интегралдың орта мәні турасындағы теоремадағы қолдансақ, онда
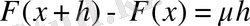
мұндағы μ-интеграл астындағы функцияның (х, ч+һ) аралығындағы дәл жоғарғы және дәл төменгі шекралықтарының арасында жататын сан. Егер һ нольге ұмтылатын болса, онда Ғ(х+һ) -Ғ(х) айырма да нольге ұмтылады, бұл айырманың нольге ұмтылуы теореманы дәлелдейді.
Егер функция f(x) [a, b] аралығында үздіксіз болса, онда мына интегралдың
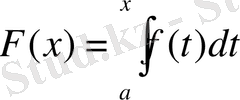
жоғарғы айнымалы шегі бойынша алынған туындысы интеграл астындағы функцияға тең болады, яғни [a, b] аралығындағы барлық нүктелер мына теңдік орындалады:
F’(x) =f(x)
Дәлелдеу. Функция f(x) [a, b] аралығында үздіксіз болғандықтан теңдіктің орнына төмендегі теңдік болады:
F(x+h) -F(x) =hf(ξ),
Мұнда x≤ξ+x+h, егер h>0 немесе х+һ≤ξ≤х, һ<0 болса.
Осы теңдіктің екі жағын һ-қа жіберіп, сонан кейін һ-тың өзін нольге ұмтылтып шекке көшсек, сонда мынадай болады:
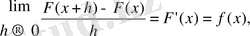
өйткені, һ нольге ұмтылатын болса, ξ х-ке ұмтылады, ал f(х) -үздіксіз функция.
Осы дәлелденген теоремадан өте қажетті мынадай қорытынды келіп шығады: егер функция f(х) үздіксіз болса, онда мына функция
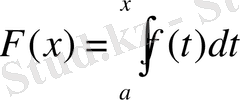
оның алғашқы функциясы болады. Сөйтіп, әрбір үздіксіз функцияның алғашқы функциясы болады.
Бұл арадан жоғарғы шегі айнымалы анықталған интегралды анықталмаған интеграл орнына қарауға болады деген де қортынды шығаруға болады.
АB кесіндісінде үздіксіз ф функциясы берілсін делік. Баяндалатын мәселе айқын болу үшін ф өспелі және оның графигі көрсетілгендей деп ұйғарайық.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz