Жиын элементтерінің қатынастары: анықтамалар, түрлері және қасиеттері


Қатынастардың түрлері
Х-Х декарттық көбейтіндісінің кез-келген ішкі жиынын X жиынының элементтерінің арасындағы қатынас X жиынындағы қатынас дейді.
Әдетте, қатынасты Р, Ọ, R әріптері арқылы белгілейді. Сонымен, егер Р қатынасы X жиынының элементтерінің арасындағы қатынас болса, онда РсХ-Х болады.
Берілген қатынасты құрайтын жұптардың компонентерінің орнын ауыстыру арқылы алынған қатынас кері қатынас деп алында. Оны Р 1 арқылы белгілейді.
Берілген қатынасты терістеу арқылы алынған қатынасты қарама-қарсы қатынас деп атайды және Р арқылы белгілейді.
Берілген жиындағы қатынасты арнайы сурет арқылы бір нүктеден екінші нүктеге бағытталған сызықтармен кескіндеуге болады. Мұндай суреттерді математикада бағдарланған графтар деп атайды. Ал жиын элемнеттерін кескіндейтін нүктелер графтың төбелері деп аталады. Графтағы басы мен соңы сәйкес келетін стрелкалар тұзақтар деп аталады.
Берілген қатынастың бірінші компонентерін абсцисса осіне, ал екінші компоненттерін ордината осіне салу арқылы табылатын қатынастың тікбұрышты координаттар жүйесіндегі бейнесі оның графигі деп аталады.
Жиынның элементтері арасындағы қатынастар үшін төмендегі қаситтер орындалады:
1. Егер X жиынындағы әрбір элемент өзімен өзі Р қатынаста болса, онда бұл қатынас рефлексивті қатынас деп аталады. Рефлексивті қасиетке ие болатын жиын графының әрбір төбесі тұзақ болады.
2. Егер X жиынындағы ешқандай элемент өзімен өзі Р қатынаста болмаса, онда қатынас антирефлексивті деп аталады.
3. ЕгерХ жиынындағы кез-келген Хжәне У элементтері үшін ХРУ-тен УРХ шығатын болса, онда оны симметриялық қатынас дейді. Симметриялық қасиетке ие болатын жиынның кез-келген екі элементі өзара стрелкамен қосылады, ал төбелерінде трақтарыда болуы мүмкін.
4. Егер X жиынындағы кез-келген X және У элементтері үшін бір мезгілде ХРУ, әрі УРХ қатынастары орыналмаса, онда Р-ны ассимметриялық қатынас деп атайды.
5. Егер X жиынындағы ХРУ және УРХ қатынастарынан х=у болады деген корытынды шықса, онда Р-ны антисимметриялық қатынас дейді. Бұл қатынастардың графында элементтер жұбы бір ғана стрелкамен қосылады және төбелерінде трақтарыда болуы мүмкін.
6. Егер X жиынындағы кез-келген х, у және г элементтері үшін хРу және уРτ -терден хРτ шықса, онда Р транзктивті қатынас деп аталады.
7. Егер X жиынындаға кез-келген х және у элементтері үшін не хРу және уРх, не х=у орыңдалса, онда Р байланыстырушы қатынас деп аталады.
8. Егер X жиынындағы Р қатынасы рефлексивті, симметриялық және транзитавтік қасиеттерге ие болса, онда оны эквиаленттік қатынас деп атайды.
Егер X жиынында эквивалентік қатынас орындалса, онда оның элементтерін өзара қиылыспайтын ішкі жиындарға (кластарға) бөлуге болады және керісінше, X жиынының элементтерін өзара қиылыспайтын ішкі жиындарға бөлуге болса, онда ол жиында эквиваленттік қатынас орындалады.
. Егер X жиынындағы Р қатынасы антирефлексивті, ассиметриялы және транзитивті болса, онда оны қатаң реттілік қатынас деп атайды.
Бұл қатынастың графында тұзақтар болмайды және кез-кежен х, у элементтер жұбын х-тен у-ке бағытталған бір ғана стрелка
жалғастырады.
Егер X жиыныдағы Р қатынасы рефлексивті, антисимметриялы және транзитивгі болса, онда оны қатаң емес реттілік қатынас деп атайды.
10. Егер X жиынындағы кез-келген х және у элементері хРу, не уРх болса, онда Р - сызықты реттілік қатынас деп, ал X сызықты жиын деп аталады.
11. Егер Р қатынасы мен сызықты реттелген X жиынының кез-келген екі элементі арасында жиын элементерінің тек шекті жиыны жатса, онда Р-ны дискреттік қатынас деп атайды.
Егер сызықты реттелген жиынның кез-келген әртүрлі элементінің арасында жататын элемент бар болса, ол жиынды да тығыз жиын деп атайды.
Жаттығулардың орындалу үлгілері
1-жаттығу. X ={4, 8, 12, 16} «х саны у санының бөлгіш» деген
қатынасы берілген.
А) Р қатынасында болатын барлық жұптарды атаңыз
б) Р қатынасының графын сызыңыз
в) Р қатынасына кері және қарама-қарсы қатынасты айтыңыз, олардың графы мен графиктерін сызыңыз
г) Р қатынасы үшін орындалатын қасиеттерін атаңыз
Шешуі: Қатынастың анықтамасы негізінде алғашқы Х-Х декарттық көбейтіндісін табайық.
Х* Х= [(4; 4) (4; 8), (4; 12), (4; 16), (8; 4), (8; 8), (8; 12), (8; 16), (12; 4)
(12; 8), (12; 12), (12:16), (16; 4), (16; 8), (16; 12), (І6; 16)
а) Р қатынасында болатын барлық жұптары атайық:
(4; 4), (4; 8), (4; 12), (4; 16), (8; 8) . (8; 16), (12; 12), (16; 16)
ә) X жиынында хРу қатынасы орындалатындай барлық (х; у) жауптар үшін х-тен у-ке қарай стрелкалар жүргізейік. Сондағы сурет Р қатынасының графы деп, ал жиын элеменггерін кескіндейтін нүктелерді графтың төбелері деп аталады.
Р қатынасының графын құру үшін х={4, 8; 12; 16} жиынының элементтерін нүктелер арқылы кескіндеп, ал қатынас орындалатын сандарды стрелкамен қосамыз. Кез-келген сан өзінің кескіні болатындықтан, басы мен соңы сәйкес келетін стрелкалар да жүргізіледі. Графтағы ондай стрелкаларды тұзақтар деп атайды.
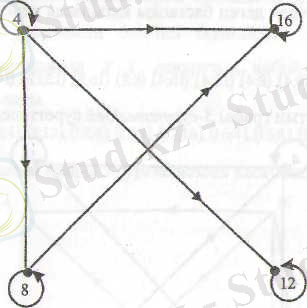
1-сурет
б) Тік бұрышты координаттар жүйесінде Р қатынасының барлық элементтерін белгілейік. Осылайша Р қатынасының графигін саламыз
2. Жаттығулар
Хжиынында Р қатынасы берілген.
А) Р қатынасында болатын барлық жұптарды атаңыз.
Б) Р қатынасының графигін салыңыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz