Ықтималдық теориясына кіріспе: оқиғалар, анықтамалар және негізгі әдістер


Кіріспе
Казіргі уакытта ықтималдықтар теориясы мен математикалық статистика әдістері барлық жаратылыстану, экономикалық және техникалық ғылымдар ғана емес, тіпті математикадан алшақ деп саналатын тіл ғылымына, педагогика мен психологияға, сондай-ақ социологияға, археологияға және т. с. с. еніп, ортақ тіл табысып, ішкі құрылыс заңдарын ашатын пәрменді кұралға айналып келеді. Бұл пән - кездейсоқ кұбылыстар заңдылығымен айналысатын математика саласы.
Ықтималдық ұғымдарының тарихи дамуы мен ғылым ретінде қалыптасуы бірнеше сатыдан өтеді. Бұл ғылымның дамуына Еаропа ғалымдары Б. Паскаль {1623- 1662), П. Ферма (1601 -1665), X. Гюйгенс (1629-1695), Я. Бернулли (1654-1775), А. Муавр (1667-1754), П. Лаплас (1749-1827), Ф. Гаусс (1777-1855), С. Луассон (1781-1840) және орыс ғалымы Буяковский (1804-1889) көп үлес қосты.
Бұл ғылымнын келесі дамуы ұлы орыс математигі Пафнутий Львович Чебышев (1821 - 1894) басқарған Петербург ықтималдықтар теориясы мектебімен байланысты. Атап айтканда, П. Л. Чебышевтың XIX ғасырдың орта кезінде жарық көрген іргелі зерттеулерінен бастап, Россияда ықтималдықтар теориясы пәрменді дамыды. Аса ірі еңбектер сіңіріп, жаңа әрі құнды нәтижеге колы жеткен, орыс-совет ғалымдары А. А. Марков (1856- 1922) . А. М. Лупунов (1887- 1918), А. Я Хинчин (1894 - 1959), А. Н. Колмогоров (1903-1986), С. Н Бериштейн (1880-1968), В. А. Романовский (1879-
1954), В. И. Слуцкий (1880-1948), В. И. Гливенко (1806- 1940) Б. В. Гнеденко (1912 туған), Ю. В. Линник (1925- 1972), Ю. В. Прохоров (1929 туған) т. т. есімдері журтшылықа кеңінен мәлім.
I Б Ө Л I М
ықтималдықтар теориясы
І тарау
КЕЗДЕЙСОҚ ОКИҒАЛАР ЖӘНЕ ОЛАРДЫҢ ЫҚТИМАЛДЫҚТАРЫ
1 . Оқиғалар. Оқиғалар алгебрасы
1. 1. Комплексті шарт, сынау, оқиға, Бұл ұғымдарды түсіндіруді мысалдардан бастайық.
- - м ы с а л. Теңгені (металл ақшаны) тептегіс еденге лақтырайық, сонда мына төмендегі құбылыстарды байқаймыз. Теңгені лақтыру үшін өзімізді, белгілі бір қалыпқа келтіреміз. Одан соң бас бармақпен теңгенің бір ұшын жоғары қарай түртіп жібереміз. Сонда ол шыр көбелек айналып, белгілі бір биіктікке дейін көтеріліп төмен қарай құлдилап, еденге түседі де, бірнеше рет секіректеп, жалпағынан не тиын жағы, не герб жағы жоғарықарап жатады. Сайып келгенде, теңге жалпағынан жатуы үшін көптеген кимыл әрекеттер жасалады, солардың жиыныкомплексті шартдеп аталады. Онын тиын (не герб) жағының. жоғары түсуі (жатуы) -осы комплексті шарттың орындалу нәтижссі -оқиғадеп аталады.
- - м ы с а л. Біртекті материалдардан жасалған симметриялы кубтың әрбір жағын 1-ден 6-ға дейінгі цифрлармен нөмірлейік. Оны бір рет лақтырғанда (комплексті шарт орындалғанда) 6 жағының бірі жоғары қарап түседі қай жағы (нөмірі) түссе де оқиға болады.
3-мысал. 760 мм қысымдағы суды 100°С-гс дейін қыздырсақ, ол буға айналады. Судың буға айналуы - оқиға, ал осы бу пайда болғанға дейінгі барлық әрекеттер жиыны комплексті шарт болады.
Қомплексті шарт термині орнына сынау, тәжірибе, эксперимент терминдерін де пайдаланады. Біз көбінесе сынау терминін қолданамыз. Бұдан былай сынау нәтижесін оқиға деп ұғамыз. Әдетте оқиғаларды үлкен әріптер А, В, С, . . . арқылы, ал бұларға қарамақарсы оқиғаларды А, В, С, . . . арқылы белгілейміз. Мысалы, теңгенің тиын жағының пайда болуы А оқиғасы болса, герб жағының пайда болуы А оқиғасымен белгіленді және т. с, с.
1. 2. Оқиғаларды кластарға бөлу.
Сынау жүргізілгенде А оқиғасы пайда болуы да, пайда болмауы да мүмкін болса, ондай оқиғаны кездейсоқ оқиға деп атайды. Мұндай оқиғаларға 1, 2-мысал жатады, өйткені сынау нәтижесінде теңгенің (кубтың) белгіленген жағының пайда боларын күн ілгері айта алмаймыз. Сынау нәтижесінде оқиға (А оқиғасы) сөзсіз пайда болатын болса, ондай оқиғаны ақиқат оқиға дейді. Сынау нәтижесінд е оқиғаның (А оқиғасы) пайда болуы мумкін болмаса, ондай оқиғаны мүмкін емес оқиға дейді.
Ақиқат оқиғаны U әрпімен, мүмкін емес оқиғаны V әрпімен белгілеу қабылданылған. Мысалы, қобдишаға салынған ақ шарлардың біреуін алсақ, оның ақ болып шығуы ақиқат
оқиға да, басқа түсте болуы мүмкін емес оқиға. Сынау жургізгенде екі оқиғаның бірі пайда болып, екіншісі пайда болмайтын оқиғаларды үйлесімсіз оқиғалар дейді. Мәселен 2-мысалдағы
, А 2 (бірінші және екінші нөмірлі жақтар) оқиғалары - үйлесімсіз оқиғалар, Бұл мысалдағы кез келген екі оқиға да үйлесімсіз. Кез келген екі оқиғасы үйлесімсіз болатын оқиғалар жиынын қос-қостан үйлесімсіз оқиғалар дейді .
Сынау жүргізілгенде оқиғаның бірінің, пайда болуы екіншісінің пайда болуын жоққа шығармайтындай екі оқиғаны үйлесімді оқиғалар деп атайды. Мысалы, кубтың жұп нөмірінің пайда болуы (А оқиғасы) мен үш санына еселік нөмір пайда болуы В оқиғасы үйлесімді. Өйткені кубтың 6- нөмірінін пайда болуын кәрсететін А 6 оқиғасы В оқиғасы пайда болғанда да, А оқиғасы пайда болғанда да пайда болуы мүмкін.
Сынау нәтижесінде мүмкін оқиғалардың әйтеуір 6іреуінің сөзсіз пайда болуы ақиқат болса, ондай оқиғаны жалғыз ғана мүмкіндікті оқиға дейді. Жалғыз ғана мүмкіндікті оқиғалар оқиғалардың толық тобын немесе оқиғалардың толық жүйесін (системасын) құрады. М. ысалы, сынау нәтижесінде кубтың алты жағының біреуі (А оқиғасы) пайда болуы сөзсіз, сондықтан
, А 2 , Аз, А 4 , А 5 , А 6 оқиғалары жалғыз ғана мүмкіндікті оқиғалар және олар оқиғалардың толық тобын құрайды. Сонымен қатар бұлар қос-қостан үйлесімсіз оқиғалар.
1. 3. Ықпималдықтың геометриялық статистикалық және аксиоматикалық анықтамалары
Бұған дейін ықтималдықтың классикалық анықтамасын келтіріп, теория негізінде түрлі есептерді шығардық. Енді ықтималдықтың одан басқа да анықтамаларын келтіре отырып классикалық анықтамамен салыстырып отырамыз.
1. 3. 1. Геометриялық анықтама. Өткен параграфта қарастырылған тәжірибе нәтижелері шекті саналымды болыл келді, практикада кездесетін есептердің басым кепшілігі бұл схемаға келе бермейді. Өйткені, тәжірибе нәтижелері саналымды шексіз, я саналымсыз жиын болуы мүмкін. Сонымен, ықтималдықтың классикалық анықтамасын сынау нәтижесінің саны шексіз тең мүмкіндікті (тең ықтималды) тәжірибеге қолдануға болмайды. Осындай жағдайды сипттауға ықтималдықтың геометриялық анықтамасы ыңғайлы. Ол үшін біз G жиынында нүкте бірқалыпты үлестірілген деп ұйғарамыз, ал мұның қандай да ішкі жиынын «g» деп белгілеуге болады (1сурет) . Ол уақытта G облысына лақтырылған нүктенің «g» облысына түсуін А оқиғасы деп белгілеп, оның ыктималдығына мынадай анықтама беруге болады.
Анықтама. g облысына лақтырылған кездейсоқ нүктенің (А оқиғасы) осы облысқа түсу ықтималдығы g өлшемінін, G облыс өлшеміне (ұзындық, аудан, көлем) катынасына тең, яғни
Мұнда да ықтималдықтың классикалық анықтамасында айтылған үш қасиет орын алады.
1°. Р(g) теріс тақбалы емес, яғни Р
0.
2°. Ақиқат оқиға ықтималдығы бірге тең, яғни Р(G) =1.
3°. Қос-қостан үйлесімсіз оқиғалар қосындысынын ықтималдығы олардың ықтималдықтарының, қосындысына тең.
Бұл соңғы қасиет үйлесімсіз оқиғалар саны шекті және саналымды шексіз болса да орын алады дейміз.
Геометриялық ықтималдықтар схемасы астрономия, атомдық физика, биология және т. с. с. салаларда пәрменді қолданыс тауып отыр. Ескертетін бір жайт - реал құбылысты сипаттауға классикалық та, геометриялық та схеманы алуға болады. Бірақ геометриялық ықтималдықтар схемасында алынған модель классикалық схемаға қарағанда айқын емес. Әрине бір реал құбылысты сипаттайтын әр түрлі модельге сәйкес түрлі ықтималдықтарды алуға болады.
Тарихи традициялық мына екі мысалды келтірейік .
1 мысал (кездесу туралы есеп) . Екі адам (А мен В) сағат 18 бен 19 аралығында кездесуге уәделескен.
Қайсысы бұрын келсе, сонысы 20 минут күтеді, сол мезгілде екіншісі кемесе қайтып кетеді. Егер әрқайсысының сол уәделескен уакытта келуі бір-біріне тәуелсіз және кездесуі кездейсоқ болса, онда А мен В-ның кездесу ықтималдығы неге тең.
Ш е шу і. А-ның уәделі жерге келу уақытын х,
теңсіздіктермен анықталады:18(сағ)
(сағ)
В-ның келуін у арқылы белгілейік. Уақыт өлшемін минут деп минут деп қабылдасақ, онда олар тек
мин
13сурет
болғанда ғана кездеседі. Бұл жағдайда барлық нәтижелер жиыны мына және
18 (сағ)
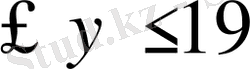 (сағ) Кездесуге қолайлы нәтижелер жиыны мына тенсіздікпен берілген:
(сағ) Кездесуге қолайлы нәтижелер жиыны мына тенсіздікпен берілген:
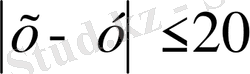 немесе
немесе
 -20
-20
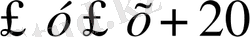 Осы колайлы нәтижелер сызылған жолақта орналасқан (13сурет) .
Осы колайлы нәтижелер сызылған жолақта орналасқан (13сурет) .
Бұл суретте
Ал, сол екі адам уәделі жерде
 0, t
0, t
 уақыт аралығында
уақыт аралығында
 уақытта кездесетін болса, онда
уақытта кездесетін болса, онда
Equation. 3
Дербес жағдайда t = 1,
Equation. 3 = 1/3, болса онда
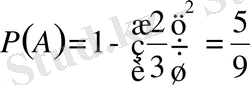
2мысал. (Бюффон есебі) . Жазықтықка бір-бірінен 2а кашьіктықта орналасқан шексіз көп параллель тузулер үйірі жүргізілген. Сол жазықтыққа үзындығы 2l-ге (l
) тең ине қалай болса солай лақтырылсын. Иненің үйір түзулерінің кем дегенде әйтеуір біреуімен қиылысу ықтималдығын анықтау керек.
Ш е ш у і.
х
арқылы кесінді ортасы 0-мен жақын тузуге дейінгі аралықты белгілейік. Ал
 аркылы иненің осы параллель түзумен қиылысу бұрышын белгілейік (2, а-сурет) . Бұл
х
және
аркылы иненің осы параллель түзумен қиылысу бұрышын белгілейік (2, а-сурет) . Бұл
х
және
 шамалары жақын түзуге қатысты кесіндінің жағдайын анықтайды. Сондықтан сынау нәтижелерінің жиыны
шамалары жақын түзуге қатысты кесіндінің жағдайын анықтайды. Сондықтан сынау нәтижелерінің жиыны
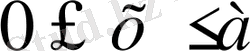 ,
,
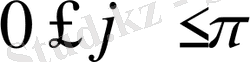 теңдсіздіктерімен сипатталады . Декарт оординаталарында (
теңдсіздіктерімен сипатталады . Декарт оординаталарында (
 ,
х)
кабырғаларының ұзындығы
а
және
,
х)
кабырғаларының ұзындығы
а
және
 болған тіктөртбұрыш болады (2, ә-сурет) .
болған тіктөртбұрыш болады (2, ә-сурет) .
Енді қолайлы нәтижелер жиыны g-ны табайық. Әрине, ине параллель түзулердің бірін қиюы үшін
болуы қажетті де жеткілікті (мұнда х
0) . Бұл теңсіздіктерді қанағаттандыратын (
, х) нүктелерін абсциссалар өсімен
бұрышын жасайтын сәулемен және
қисығымен шектелген фигура ішінде жатады. Олай болса, іздеген ықтималдық
Р(А) =
Яғни
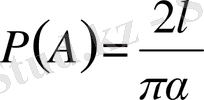
Бұл есеп нәтижесін ғалымдар
дің жуық мәнін анықтауға пайдаланған. Мұндай инені лақтырып тәжірибе жүргізгендер көп болған. Бұлар инені п рет лақтырғанда түзуді қанша ретінде қиюын (m-ді) анықтап отырған. Бұл жағдайда Р(А) ықтималдығы f(А) =m/п салыстырмалы жиілігіне (ықтималдығына) жақындайды, яғни
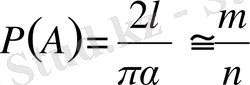 (2)
(2)
Бұл өрнектен
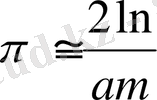
Осы фомуланы лайдаланып
мәнін табу үшін мына кестедегі мәліметтерді пайдаланайық.
Жылы
Сызықты қию саны
 -дің жуық мәні
-дің жуық мәні
Вольф
Рейн
1850 1925
5000
2520
2532
859
3, 1596 3, 1795
Оны мына мысалда көрсетейік. Вольф ине ұзындығын 7, 2см етіп, ал іргелес параллель тузулер аралығын 9см (яғни 2l = 7, 2 см, 2а=9см ) етіп алады. Сонда
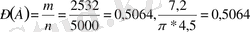
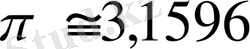
1. 3. 2. Статистикалық заңдылық және ықтималдықтың жиіліктік анықтамасы .
Құбылыстарды сипаттауға ыктималдықтың статистикалық анықтамасын колданайық. Статистикалық анықтама тәжірибені (сынауды) сан рет қайталап, нәтижелерін (оқиғаны) регистрациядан өткізуге (тізбегін жасауға) сүйенеді. Сынау көп жургізілгенде оқиғаныд бірнеше рет пайда болуы не болмауы мумкін. Оқиғаның пайда болу (болмау) санын бұдан былай жиілік немесе абсолюттік жиілік дейтін боламыз. Ал жиіліктің барлық сынау санына қатынасын салыстырмалы жиілік дейміз. Сонда сынаудың жалпы санын п десек А оқиғасының қайыра пайда болу санын (жиілігін) m десек, онда А оқиғасының салыстырмалы жиілігі мынаған тең болады: f (А) = т/п. Жүргізілген сынау саны аз болса, жиілігі тұрақты болмай бір сынаудан екінші сынауға дейінгі өзгеріс артып отырады. Ал сынау жеткілікті дәрежеде қайталанып отырса, онда А оқиғасының салыстырмалы жиілігі тұрақтана түседі. Мұндай жағдай физика техникалық бақылауларда, биологияда, экономикада және т. с. с. байқалады.
Бұл айтылғандарға алдымен төменгі мысалдармен түсініктеме берейік.
3 -м ы с а л. Теңгені п рет лақтырып, оның герб жағының пайда болу жиілігін анықтау үшін Бюффон және К. Пирсон жургізген тәжріибе қорытындылары 3-таблицада келтіріліп отыр.
3-кесте
Эксперимент жүргізгендер
Лақтыру саны
Герб тусу саны
Салыстырмалы
ЖНіЛіГі
Бьюффон К. Пирсон К. Пирсон
4040 12000 24000
2048 6019 12012
0, 5080
0, 5018
0, 5005
Бұл келтірілген мысалдан сынау саны мейлінше көп болса, салыстырмалы жиілік мәні тұрақтылық қалыпқа түсетінін байқаймыз, біздің мысалымызда 0, 5-ке жуықтайды. Екінші сөзбен айтқанда, кездейсоқ құбылыстарда қандай да объективті қасиеттер бар екені және оның тұрақтануға бейімділігі сезіледі.
Бұл қасиет сынау саны артқан сайын айқындала түседі, ол қасиет кандай да бір тұрақты шамамен (санмен) өлшенеді. Бұл шама бақылауға түскен құбылыстың объективті сандық сипаты болып табылады. Осы тұрақтыны (санды, мөлшерді) кездейсоқ оқиға А-ның ықтималдығы дейміз. Сөйтіп оны бұрынғыша Р(А) арқылы белгілейміз. Осылай анықталған кездейсоқ оқиға ықтималдығын статистикалық ықтиамалдық деп атайды. Сонымен, ықтималдықтың статистикалық анықтамасында Р(А)
f(А) деп қабылдайды.
Ықтималдықтың ілгеріде келтірілген қасиеттері статистикалық тұрғыдан анықтағанда да орындалады:
1
Салыстырмалы жиілік m/п теріс таңбалы болуы мумкін емес, өйткені
демек,
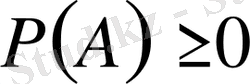
2°. Ақиқат оқиға сынауды эрбір қайталауда пайда болады, сондықтан т = п демек, Р(А) =1
3°. А және В оқиғалары үйлесімсіз болса, бұлардың косындысының ықтималдығы олардың ықтималдықтарының қосындысына тең, яғни п - сынаудың жалпы саны, А оқиғасының пайда болу жиілігі т 1 В оқиғасының пайда болу жиілігі
болса, онда
(3)
Классикалық анықтамада келтірілген осы негізгі үш қасиеттен шыққан басқа қасиеттер орындалады. Ықтималдықтардың жоғарыда аталған қасиеттері әр түрлі кездейсоқ оқиғалар жүйесі үшін орын алады.
Классикалық анықтама негізінде ықтималдықтар теориясын құрған сияқты, статистикалық анықтама негізінде де аталмыш теорияны кұруға болады. Назар аударатын бір мәселе - статистикалық ықтималдықтың сандық мәнінің белгісіз болуы. Әдетте, сынау саны өте көп болғанда ықтималдық мәніне де А-ның салыстырмалы жиілігінің өзі алынады, не осы салыстырмалы жиілікке жуық сан алынады. Ондай санға, мысалы жеткілікті үлкен бірнеше сериядан іріктеліп алынған салыстырмалы жиіліктің арифметикалық ортасы алынады. Бұл анықтаманын, іс жүзінде орындалатын түрлі зерттеулерде ерекше мәні бар, өйткені бас жиынды зерттеуге мүмкіндік болмай қалады, сондықтан оның, бөлігін (таңдаманы) зерттеуге мәжбүр боламыз. Сөйтіп тандаманы зерттеу нәтижесінде кездейсоқ оқиғанын, салыстырмалы жиілігін анықтаймыз. Осы таңдамадағы салыстырмалы жиілік арқылы ықтималдықтың сандық мәнін бағалаймыз бұл қарастырып отырған кұбылыстың сандық сипаттамасы болып табылады. Мұның, теориялық негіздемесі үлкен сандар заңына сүйенеді. Сонымен, ықтималдықтар теориясы мен практиканы (статистиканы) ұштастыратын маңызды дәнекер модель - үлкен сандар заңы. Бұл заңның математикалық дәлелдемелерін кейінге қалдыра отырып, қарапайым негіздемесін келтірейік. Бұл негіздеме практикалық сенімділік принцип ұғымына байланысты. Сондықтан алдымен осы ұғымды түсіндірейік. Іс жүзінде мүмкін емес және ақиқат оқиғалар орнына «практикалық мүмкін емес» және «практикалық ақиқат» оқиғалар болады. Өйткені қандай да оқиға ықтималдығы нөлге жуық болса, ондай оқиғалар ете-мөте сирек пайда болатын емір тәжірибесінен аян.
Екінші сөзбен айтқанда, кейбір оқиға ықтималдығы мейлінше кіші болса, ондай оқиға бір рет жүргізілген сынауда пайда болмайды деп ұйғарамыз. Бұнда ол оқиғаның әйтеуір бір уақытта пайда болуын жоққа шығармаймыз. Бұл принципті біз әрдайым күнделікті өмірімізде қолданып отырамыз. Сонымен, практикалық мүмкін емес оқиға деп ықтималдығы нөлге тепе-тең. емес, бірақ оған мейлінше жуық болған бір рет жүргізілген сынауда пайда болмайды делінген оқиғаны айтамыз. «Практикалық ақиқат» оқиғаны да «практикалық мүмкін емес» оқиға сияқты анықтайды. Өйткені оқиға мүмкін емес болса, оған қарама-қарсы оқиға ақиқат оқиға болады. Олай болса, практикалық ақиқат оқиға деп ықтималдығы бірге тең емес, бірақ оған мейлінше жуық болған оқиғаны айтамыз. Ықтималдықтар теориясының практикалық колданылуы осы практикалық ақиқат және практикалық мүмкін емес оқиғалар ұғымдарына сүйенеді. Сондықтан бұл ұғымдардың алатын орны үлкен. Айтылып отырған «практикалық ақиқаттық» (сенімділік) және «практикалық мүмкін еместік» (сенімсіздік) ұғымдарын кейде практикалық сенімділік принципі деп атайды. Бұл принциптің анықтамасы мынадай. Қарастырып отырған процесте А оқиғасының ықтималдығы мейлінше аз (мейлінше үлкен) болса, онда тәжірибе бір рет орындалғанда А оқиғасының пайда болмауын (болуын) іс жүзінде үлкен сенімділікпен (ықтималдықпен) айта аламыз. Практикалық сенімділік принципін математикалық дәлелдеуге де болмайды. Өйткені, оқиғаның практикалық сенімділігі (сенімсіздігі) оның ықтималдығына байланысты анықталады. Мысалы, самолеттің авария болу ықтималдығы 0, 05 тіпті 0, 01 болса, онда авиациямен жолаушыларды тасу іс жүзінде пайдаланылмаған болар еді. Ал егер де екі қала аралығын өлшеуде кететін қате ықтималдығы 0, 05 болса, мысалы, әр километрге 50 см қате болса, одан ешқандай зиян болмайды. Бұл қатені ескермеуімізге болады. Сонымен, ықтималдықтар теориясының әрбір қолдану саласына тән өзінін, практикалық сенімділігі (ықтималдығы) беріледі. Оны біз шекаралық ықтималдық дейміз. Мұндай шекаралық ықтималдыққа көп жағдайда 0, 90; 0, 95; 0, 99 сандары алынады. Аталған сандарды, мысалы 0, 95 ықтималдығын былай ұғамыз: егерде кандай да бір оқиғаны бақылау үшін 100 рет тәжірибе жүргізілсе, оның 95 проценттей нәтижесін дұрыс деп айта аламыз да, 5 проценттей қателесуіміз мүмкін.
1. 3. 3. Ықтималдықтың аксиоматикалық анықтамасы. Біз бірінші параграфта оқиғалар алгебрасы туралы айтқанда сынау нәтижесі шекті оқиғалар болыл оларға қолданатын операциялар шекті де, саналымды шексіз де және саналымсыз да болуы мумкіндігін ескерткен едік. Енді оқиғалар алгебрасы ұғымын кеңейтеміз. Бұл үшін оқиға болатын ішкі жиындар класын кұрудың қажеттігі туады.
2. Қосылыстар теориясы элементтері.
Берілген Ω жиынының элементтерінен құрылған оған кірме әр түрлі
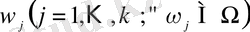 жиындары қосылыстар (комбинациялар) деп, математиканың қосылыстар теориясын зерттейтін бөлімі комбинациялық талдау деп аталады. Бұл бөлімнің негізгі принципі- көбейту ережесі : егер әрбір
жиындары қосылыстар (комбинациялар) деп, математиканың қосылыстар теориясын зерттейтін бөлімі комбинациялық талдау деп аталады. Бұл бөлімнің негізгі принципі- көбейту ережесі : егер әрбір
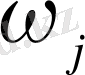 қосылысын
қосылысын
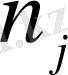 тәсілмен құру мүмкін болса, онда бірге алғанда олардың бәрі
тәсілмен құру мүмкін болса, онда бірге алғанда олардың бәрі
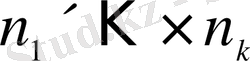 тәсілмен құрылады.
тәсілмен құрылады.
Әр элементіне сандардың натурал қатарынан номер тағылған шекті жиынды реттелген жиын дейміз. Реттелген шексіз жиын санамалы жиын делінеді.
Бір-бірінен элементтерінің ретімен (орындарымен) ғана ажыратылатын n элементті әр түрлі (реттелген) жиындар n элементтен жасалған орынауыстырулар деп аталады. Олардың саны
 ! (2. 1)
! (2. 1)
Реттелген болуы міндетті емес Ω және ω (ω
 ) жиындары сәйкес n және m (m≤n) элементтен құрылған делік. Бір-бірінен құрамымен ғана (реті ескерілмей) ажыратылатын барлық ω қосылыстары n элементтен
) жиындары сәйкес n және m (m≤n) элементтен құрылған делік. Бір-бірінен құрамымен ғана (реті ескерілмей) ажыратылатын барлық ω қосылыстары n элементтен
m-нен жасалған терулер деп аталады. Олардың саны
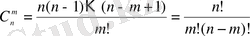 (2. 2)
(2. 2)
Ньютон биномның формуласын енді
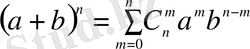 (2. 3)
(2. 3)
түрінде жазуға болатындықтан (2. 3) сандары биномдық коэффициенттер деп те аталады. Олардың «симметриялық қасиеті» бар және рекурренттік қатынастарды қанағаттандырады:
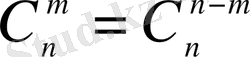 ,
,
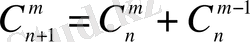 (2. 4)
(2. 4)
Жеке жағдайда: a=b=1 (2. 4) -тен
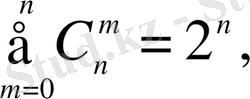
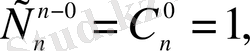

Бір-бірінен не құрамымен, не элементтерінің ретімен ажыратылаты n элементтен m-нен (m≤n) жасалған қосылыстар n элементтен m-нен жасалған орналастырулар деп аталады. Әрбір n элементтен m-нен жасалған теруден орын ауыстырулар арқылы m! орыналастырын жасауға болады. Ендеше, n элементтен m-нен жасалған орналастырулардың саны
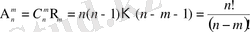 (2. 5)
(2. 5)
Шекті (n элементі бар, реттелген болуы міндетті емес) Ω жиыны кездейсоқ үлгіде сәйкес
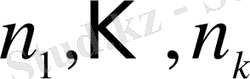 элементтен тұратын k кірме жиындарға
элементтен тұратын k кірме жиындарға
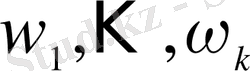
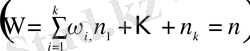 бөлшектенген десек, бөлшектеу әдістерінің саны
бөлшектенген десек, бөлшектеу әдістерінің саны
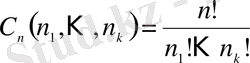 (2. 6)
(2. 6)
Бұл (полиномдық тәсіл) биномдық схеманың жалпыланған түрі. Шынында да, (2. 6) -де
 k=2 (
k=2 (
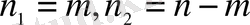 ) десек, (2. 2) -ке келеміз.
) десек, (2. 2) -ке келеміз.
Енді Ω жиынына кірме құрамында
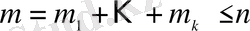
элементі бар реттелмеген қосылыс құралық. Әрбір
 -ден
-ден
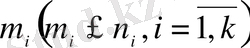 элемент алсақ, (2. 2) -нің және көбейту ережесінің негізінде мұндай қосылыстардың саны
элемент алсақ, (2. 2) -нің және көбейту ережесінің негізінде мұндай қосылыстардың саны
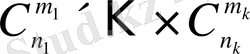
өрнегімен анықталады. Бір ғана
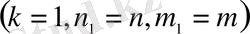 қосылыс үшін бұл өрнек (2. 2) -ге айналады, яғни полиномдық схема биномдық жүйеге ауысады.
қосылыс үшін бұл өрнек (2. 2) -ге айналады, яғни полиномдық схема биномдық жүйеге ауысады.
2-есеп. Сөреге (төртбұрышты) тәуекел қойылған 8 кітаптың қалаулы екеуі қатар орналасуының ықтималдығын табыңыз. 0
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz