Математикалық талдауға кіріспе: нақты сандар, функциялар, шектер және туындылар


Тақырып № 1
1. Математикалық талдауға кіріспе
Нақты санның геометриялық бейнесі-сандар өсіндегі нүкте және керісінше, сандар өсіндегі әрбір нүкте нақты санды анықтайды. Сондықтан «нақты сан», «сандар өсіндегі нүкте» терминдері бір мағыналы, яғни синонимді сөздер ретінде қолданылады.
Нақты сандар жиыны
рационал
және
иррационал
сандар жиындарының біріктірілуінен тұрады.
Рационал
сан деп екі бүтін санның қатнасы ретінде өрнектелетін санды айтады. Бұл сан шекті ондық бөлшек немесе периодты шексіз ондық бөлшек түріне келтіріледі. Иррационал сан периодты емес шексіз ондық бөлшек түрінде өрнектеледі. Егер сандар өсіндегі нүктенің координат басына дейінгі қашықтығы бірлік кесіндімен (масштабпен) өлшемдес болса, онда бұл нүкте рационал санның, өлшемдес болмаса иррационал санның бейнесі болады. Рационал сандар жиыны
 , иррационал сандар жиыны
, иррационал сандар жиыны
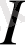 , ал нақты сандар жиыны
, ал нақты сандар жиыны
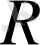 әріпімен белгіленеді және
әріпімен белгіленеді және
 болады.
болады.
«Нақты сандар жиыны» мен «нақты сандар өсіндегі нүктелер жиыны» туралы ұғымдар бір мағынада қолданылады да, қысқаша «сандар жиыны» немесе «нүктелер жиыны» деп айтылады.
Екі санмен шектелген нүктелер жиыны
аралық
деп аталады да
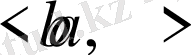 деп белгіленеді. Егер аралықты шектейтін нүктелер осы жиынға енсе, онда бұл аралық
сегмент
деп аталады да
деп белгіленеді. Егер аралықты шектейтін нүктелер осы жиынға енсе, онда бұл аралық
сегмент
деп аталады да
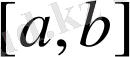 деп, ал енбесе
интервал
делінеді де,
деп, ал енбесе
интервал
делінеді де,
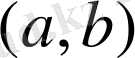 деп белгіленеді; осы нүктелердің біреуі еніп екіншісі енбесе, онда аралық
жартылай интервал
немесе
жартысегмент
деп аталады да
деп белгіленеді; осы нүктелердің біреуі еніп екіншісі енбесе, онда аралық
жартылай интервал
немесе
жартысегмент
деп аталады да
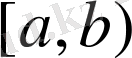 немесе
немесе
 деп белгіленеді. Интервал өзіне енетін кез келген нүктенің
маңайы
деп аталады. Центрі
деп белгіленеді. Интервал өзіне енетін кез келген нүктенің
маңайы
деп аталады. Центрі
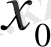 нүктесінде болатын ұзындығы
нүктесінде болатын ұзындығы
 -ге тең интервал осы нүктенің
-ге тең интервал осы нүктенің
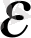 -маңайы деп аталды да
-маңайы деп аталды да
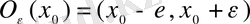 деп белгіленеді.
деп белгіленеді.
Нақты сандар жиынының негізгі қасиеті-оның үзіліссіздігі. Бұл қасиет төмендегі теорема түрінде айтылады:
Теорема 1 Ұзындықтары нөлге ұмтылатын, бірінің ішінде бірі орналасқан сегменттердің бәріне ортақ тек қана бір нүкте бар болады.
Төмендегі суретте осы теореманың геометриялық нұсқасы көрсетілген.

.



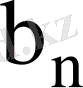
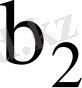

Мұндағы
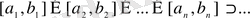 және
және
 сегментінің ұзындығы
сегментінің ұзындығы
 нөлге ұмтылатын шама, ал
нөлге ұмтылатын шама, ал
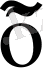 осы сегменттердің бәріне ортақ нүкте.
осы сегменттердің бәріне ортақ нүкте.
Өлшеу процесін қолдануға болатын әрбір объектің сандық мәні шама деп аталады. Табиғатты зерттейтін ғылым саласының тек өзіне тән шамалары болады. Атап айтқанда: физикада−салмақ, масса, жылу сыйымдылығы т. с. с. ; химияда-атомдық салмақ, валенттілік, т. т. ; геометрияда−кесіндінің ұзындығы, фигураның ауданы, дененің көлемі т. с. с.
Белгілі бір сандық мәнін сақтайтын
шама тұрақты
деп аталады. Әр түрлі сандық мәндер қабылдай алатын шама
айнымалы
делінеді. Әдетте, тұрақты шама латын алфавитінің алғашқы әріптерімен
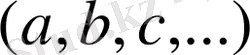 айнымалы шама соңғы әріптерімен
айнымалы шама соңғы әріптерімен
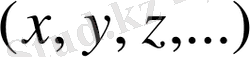 белгіленеді.
белгіленеді.
2. Функция түсінігі
2. 1Функцияның анықтамасы.
Айталық, бізге нақты сандардан тұратын
 және
және
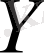 жиындары берілсін.
жиындары берілсін.
Анықтама.
Егер белгілі бір ереже немесе заң бойынша
 жиынының әрбір элементі
жиынының әрбір элементі
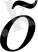 -ке
-ке
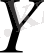 жиынының тек қана бір элементі
жиынының тек қана бір элементі
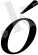 сәйкес келсе, онда
сәйкес келсе, онда
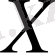 жиынында бір мәнді
жиынында бір мәнді
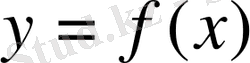 функциясы анықталған дейді. Бұл ережені немесе заңды
функциясы анықталған дейді. Бұл ережені немесе заңды
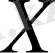 жиынын
жиынын
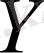 жиынына бейнелеу деп те атайды.
жиынына бейнелеу деп те атайды.
Осы анықтамадағы
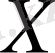 жиынын
жиынын
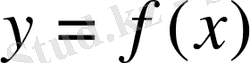 функциясының анықталу облысы, ал
функциясының анықталу облысы, ал
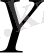 жиынын
жиынын
 функциясы мәндерінің жиыны немесе функцияның өзгеру облысы деп,
функциясы мәндерінің жиыны немесе функцияның өзгеру облысы деп,
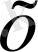 - ты тәуелсіз айнымалы немесе аргумент деп, ал
- ты тәуелсіз айнымалы немесе аргумент деп, ал
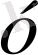 - ті тәуелді айнымалы немесе функциясы деп атайды.
- ті тәуелді айнымалы немесе функциясы деп атайды.
Тәуелсіз айнымалы
 - тың кейбір
- тың кейбір
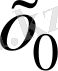 мәніне сәйкес тәуелді айнымалы (функция)
мәніне сәйкес тәуелді айнымалы (функция)
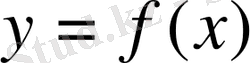 -тің мәнін функцияның
-тің мәнін функцияның
 болғандағы (немесе
болғандағы (немесе
 нүктесіндегі) мәні деп атайды және
нүктесіндегі) мәні деп атайды және
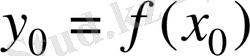 символымен белгілейді.
символымен белгілейді.
Мысалы,
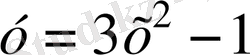 функциясы берілсе, оның
функциясы берілсе, оның
 нүктесіндегі мәні
нүктесіндегі мәні
 .
.
Егер
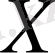 сан осінің бойында жатқан жиын болса, онда
сан осінің бойында жатқан жиын болса, онда
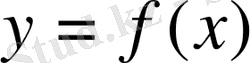 функциясының анықталу облысы не интервал
функциясының анықталу облысы не интервал
 , не сегмент
, не сегмент
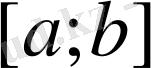 , не жартылай түзулер
, не жартылай түзулер
 немесе бүкіл сан осі
немесе бүкіл сан осі
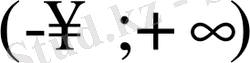 болуы мүмкін. Сонымен қатар функцияның анықталу облысы бірнеше аралықтың бірігуі болуы мүмкін.
болуы мүмкін. Сонымен қатар функцияның анықталу облысы бірнеше аралықтың бірігуі болуы мүмкін.
Мысалы,
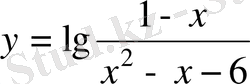 функциясын қарастырайық. Бұл функция айнымалы
функциясын қарастырайық. Бұл функция айнымалы
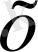 - тың мына
- тың мына
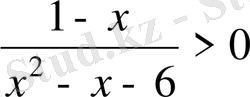 теңсіздігін қанағаттандыратын мәндерінде анықталған. Сонда бұл теңсіздіктен
теңсіздігін қанағаттандыратын мәндерінде анықталған. Сонда бұл теңсіздіктен
 немесе
немесе
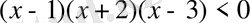 теңсіздігі шығады. Демек, берілген функцияның анықталу облысы екі аралықтан тұрады:
теңсіздігі шығады. Демек, берілген функцияның анықталу облысы екі аралықтан тұрады:
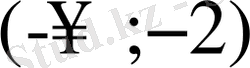 және
және
 . Яғни,
. Яғни,
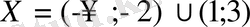 .
.
Бір
 жиынында берілген
жиынында берілген
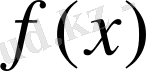 және
және
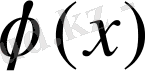 функцияларына қосу
функцияларына қосу
 , азайту
, азайту
 , көбейту
, көбейту
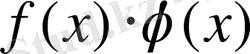 , бөлу
, бөлу
 амалдарын қолдануға болады, сонда осы амалдар орындалғаннан кейін шығатын функциялардың да анықталу облысы
амалдарын қолдануға болады, сонда осы амалдар орындалғаннан кейін шығатын функциялардың да анықталу облысы
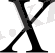 немесе оның бөлігі болуға тиіс.
немесе оның бөлігі болуға тиіс.
Мысалы, мына
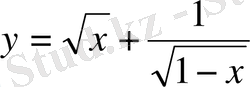 формуламен берілген функцияны қарастырайық. Бұл функция екі функцияның қосындысынан тұрады. Олардың біреуі
формуламен берілген функцияны қарастырайық. Бұл функция екі функцияның қосындысынан тұрады. Олардың біреуі
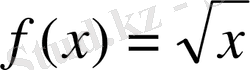 , ал екіншісі
, ал екіншісі
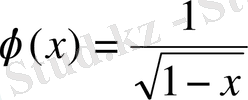 . Бірінші функцияның анықталу облысы
. Бірінші функцияның анықталу облысы
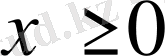 , яғни
, яғни
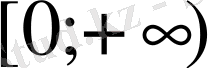 . Екінші функцияның анықталу облысы
. Екінші функцияның анықталу облысы
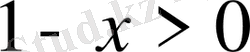 , немесе
, немесе
 . Сонда осы екі функцияның қосындысы болып табылатын бастапқы
. Сонда осы екі функцияның қосындысы болып табылатын бастапқы
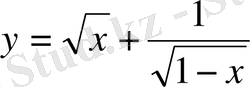 функциясының анықталу облысы (қосылғыш функциялардың анықталу облыстарының көбейтіндісі) жартылай интервал
функциясының анықталу облысы (қосылғыш функциялардың анықталу облыстарының көбейтіндісі) жартылай интервал
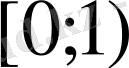 болады.
болады.
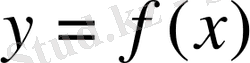 функциясының графигі
деп, координаттары берілген функционалдық тәуелділікті қанағаттандыратын, жазықтықтағы нүктелер жиынын айтады,
функциясының графигі
деп, координаттары берілген функционалдық тәуелділікті қанағаттандыратын, жазықтықтағы нүктелер жиынын айтады,
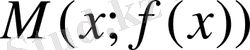 нүктелер жиыны.
нүктелер жиыны.
Функциялардың графиктері көбінесе қисық сызықтар немесе түзулер болады.
2. 2Функцияның берілу тәсілдері .
Функцияның берілуінің бірнеше тәсілдері бар. Солардың негізгілері - аналитикалық, таблица түрінде, графикпен және сөзбен берілу тәсілдері.
Айнымалылар арасындағы сәйкестік формуламен берілсе, онда функция аналитикалық түрде берілді дейді.
Мысалы,
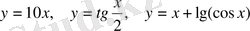 .
.
Аналитикалық тәсілмен берілген функцияның ықшамдығы оның зерттеулерде қолданылуының қолайлығын арттырады және берілген функцияны зерттегенде математиканың аппаратымен пайдалануға өте жақсы бейімделген.
Функцияның таблицалық әдіспен берілу тәсілі эксперименттік жұмыстарда қолданылады. Мұның артықшылығы аргументтің әрбір мәніне сәйкес функцияның мәні тікелей табылатындығында. Сонымен бірге аргументтің өзгеруіне байланысты функцияның өзгеру заңдылығы таблицадан байқалмайды және математикалық амалдар қолдануға өте ыңғайсыз.
Функцияның графикпен берілу тәсілі көп тараған әдіс. Оның басқалардан артықшылығы - оның көрнектілігінде. өйткені аргументтің өзгеруіне байланысты функцияның өзгеруінің бағыттарын тыңғылықты байқап отыруға болады.
2. 3Функциялардың классификациясы.
Негізгі элементар функциялар
деп келесі функцияларды айтады: тұрақты функция
 , дәрежелік функция
, дәрежелік функция
 (
(
 - кез келген сан), көрсеткіштік функция
- кез келген сан), көрсеткіштік функция

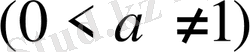 , логарифмдік функция
, логарифмдік функция

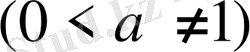 , тригонометриялық функциялар:
, тригонометриялық функциялар:
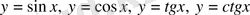 және кері тригонометриялық функциялар:
және кері тригонометриялық функциялар:
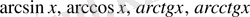 .
.
Алгебралық амалдарды, тиісті композицияларды қолданып жоғарыда аталған негізгі элементар функциялар тобынан құрылған күрделі функцияларды
элементар функциялар
деп атайды. Мысалы,
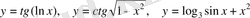 .
.
Барлық элементар функциялар алгебралық және трансценденттік функциялар болып екі класқа бөлінеді. Алгебралық функцияларға бүтін-рационал, бөлшек-рационал, иррационал функциялар жатады.
Кез келген иррационал емес функция трансценденттік функция болып табылады. Мысалы,
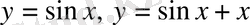 және т. с. с.
және т. с. с.
Мысалы,
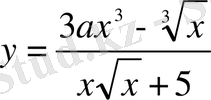 - алгебралық, ал
- алгебралық, ал

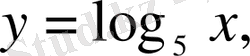
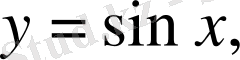
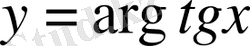 т. б, - трансценденттік функциялар.
т. б, - трансценденттік функциялар.
Айқындалған және айқындалмаған функциялар .
 түрінде берілген функция айқындалған деп аталады. Мысалы,
түрінде берілген функция айқындалған деп аталады. Мысалы,
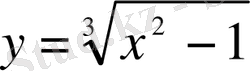 ,
,

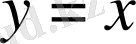 - айқындалған функциялар.
- айқындалған функциялар.
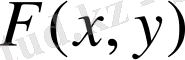 түрінде берілген функция айқындылмаған деп аталады, мысалы,
түрінде берілген функция айқындылмаған деп аталады, мысалы,
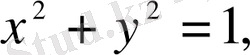
 - айқындалмаған функциялар.
- айқындалмаған функциялар.
Бір мәнді және көп мәнді функциялар.
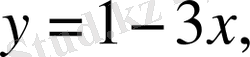
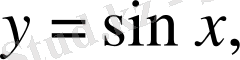
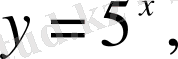 - бір мәнді, ал
- бір мәнді, ал
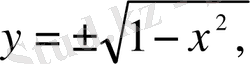

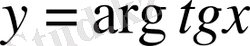 - көп мәнді функциялар.
- көп мәнді функциялар.
Кері функция. Берілген функцияға кері функцияның болу шарты:
Егер
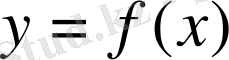 функциясы
функциясы
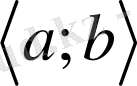 аралығында бірсарынды және бір мәнді болып, осы аралықта
аралығында бірсарынды және бір мәнді болып, осы аралықта
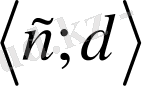 аралығында бейнелесе, онда кері функция
аралығында бейнелесе, онда кері функция
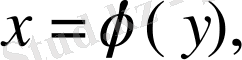 бар болады және
бар болады және
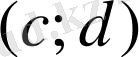 аралығында бір мәнді және бірсарынды функция болады.
аралығында бір мәнді және бірсарынды функция болады.
Мысалы
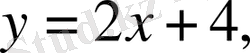 сандар өсінде анықталған және осы аралықта өспелі функция. Сондықтан
сандар өсінде анықталған және осы аралықта өспелі функция. Сондықтан
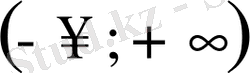 аралығында анықталған
аралығында анықталған
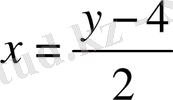 кері функция бір мәнді және бірсарынды. Осы функциядағы аргументі мен функцияның әдеттегідей
кері функция бір мәнді және бірсарынды. Осы функциядағы аргументі мен функцияның әдеттегідей
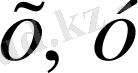 деп белгілесек, бұл функция,
деп белгілесек, бұл функция,
 түрінде жазылады. Демек,
түрінде жазылады. Демек,
 пен
пен
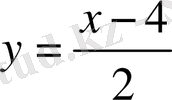 - функциялары өзара кері болады.
- функциялары өзара кері болады.
Дәл сол сияқты
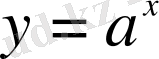 және
және
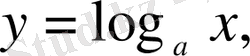 функциялары өзара кері.
функциялары өзара кері.
Күрделі функция.
 функциясы
функциясы
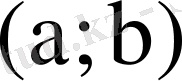 аралығында анықталып өзгеру облысы
аралығында анықталып өзгеру облысы
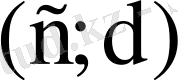 болсын және
болсын және
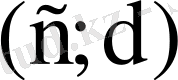 аралығында
аралығында
 функциясы анықталсын. Соңғы теңдіктегі
функциясы анықталсын. Соңғы теңдіктегі
 - ті оның мәнімен ауыстырып,
- ті оның мәнімен ауыстырып,
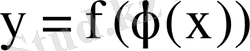 функциясына келеміз. Бұл жаңа функция
функциясына келеміз. Бұл жаңа функция
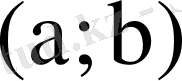 аралығында анықталған. Осы функцияны функциядан функция алу әдісімен анықталған
күрделі функция
деп атайды. (Функциялар суперпозициясы) .
аралығында анықталған. Осы функцияны функциядан функция алу әдісімен анықталған
күрделі функция
деп атайды. (Функциялар суперпозициясы) .
Мысалы:
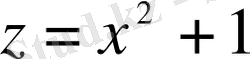 ,
,
 , деп алып,
, деп алып,
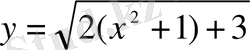 - күрделі функциясын кұрамыз.
- күрделі функциясын кұрамыз.
Тақырып № 2
Тізбек және тізбектің шегі
Натурал сандар жиынында анықталған
 функциясының мәндерін сан тізбегі немесе тізбек деп атайды.
функциясының мәндерін сан тізбегі немесе тізбек деп атайды.
Егер
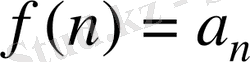 тізбегі берілсе, оны
тізбегі берілсе, оны
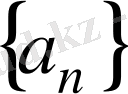 символымен белгілейді немесе былай жазады:
символымен белгілейді немесе былай жазады:

Анықтама 1
. Егер кез келген
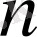 үшін
үшін
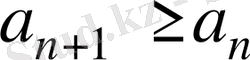 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
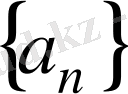 тізбегін өспелі дейді.
тізбегін өспелі дейді.
Анықтама 2
. егер кез келген
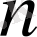 үшін
үшін
 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
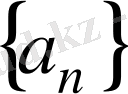 тізбегін кемімелі дейді.
тізбегін кемімелі дейді.
Анықтама 3
. егер кез келген
 үшін
үшін
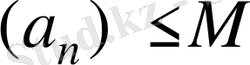 теңсіздігін қанағаттандыратындай оң
теңсіздігін қанағаттандыратындай оң
 саны табылса, онда
саны табылса, онда
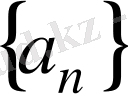 тізбегін шектелген деп атайды.
тізбегін шектелген деп атайды.
Анықтама.
Егер әрбір алдын ала берілген
 санына сәйкес
санына сәйкес
 натурал саны табылса және кез келген
натурал саны табылса және кез келген
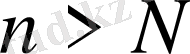 нөмірлері үшін
нөмірлері үшін
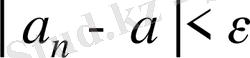 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
 санын
санын
 тізбегінің шегі деп атайды. Жазылуы:
тізбегінің шегі деп атайды. Жазылуы:
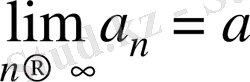 немесе
немесе
 ұмтылғанда
ұмтылғанда
 деп жазады.
деп жазады.
Мысалы,
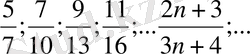 тізбектің шегін табу керек.
тізбектің шегін табу керек.
Шешімі.
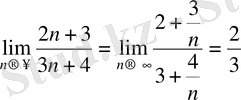 болады.
болады.
Анықтама. Шегі бар тізбекті жинақты деп, шегі жоқ тізбекті жинақсыз деп атайды. Егер тізбектің шегі бар болса, онда тізбек шектелген болады. Жинақты тізбектің бір ғана шегі бар. Жоғары (төменгі) жағынан шектелген өспелі (кемімелі) тізбектің шегі бар.
Анықтама . Егер тізбектің шегі нөльге тең болса, онда мұндай тізбекті шексіз аз деп атайды.
Теорема 1 . Екі шексіз аз тізбектердің қосындысы шексіз аз болады.
Теорема 2 . Шектелген тізбектің шексіз аз тізбекке көбейтіндісі шексіз аз тізбек болады.
Анықтама
. Егер кез келген
 саны үшін
саны үшін
 нөмірі табылып, барлық
нөмірі табылып, барлық
 үшін
үшін
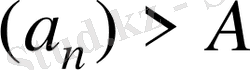 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
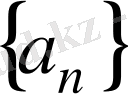 тізбегін шексіз үлкен шама дейді және былай жазады:
тізбегін шексіз үлкен шама дейді және былай жазады:
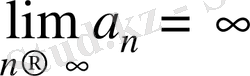 .
.
Теорема 3
. Егер
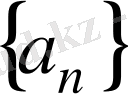 тізбегі,
тізбегі,
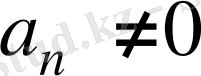 шексіз үлкен болса, онда
шексіз үлкен болса, онда
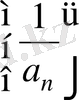 тізбегі шексіз аз және керісінше
тізбегі шексіз аз және керісінше
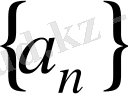 тізбегі шексіз аз болса, онда
тізбегі шексіз аз болса, онда
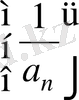 тізбегі шексіз үлкен.
тізбегі шексіз үлкен.
Теорема 4.
Егер
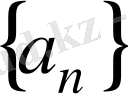 және
және
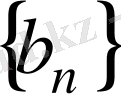 тізбектері жинақты болса, онда
тізбектері жинақты болса, онда
1)
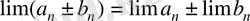 ;
;
2)
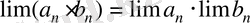 ;
;
3)
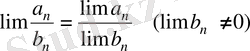 ;
;
4)
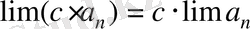 .
.
Егер
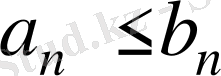 , онда
, онда
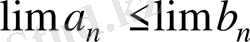
Анықталмаған өрнектер. Ақырлы шегі бар шамаларға арифметикалық амалдар қолдану нәтижесінде шекке көшкенде ешбір мазмұны жоқ, анықталмаған өрнекте деп аталатын, өрнектер шығуы мүмкін. Ондай жағдайларда айнымалы шаманың шектік мәнін табуға көшпес бұрын шыққан өрнектерді түрлендіру керек.
1) берілген айнымалылар
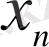 мен
мен
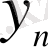 үшін
үшін
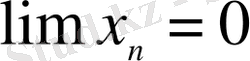 және
және

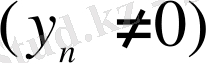 болсын. Онда олардың қатынасының
болсын. Онда олардың қатынасының
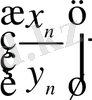 шегі
шегі
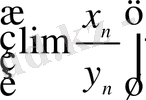
 түріндегі анықталмағандық болады. Себебі бұл екі айнымалының өзгеру заңына байланысты, бұл шек неше түрлі мәнге ие болуы мүмкін немесе шектің болмауы да мүмкін.
түріндегі анықталмағандық болады. Себебі бұл екі айнымалының өзгеру заңына байланысты, бұл шек неше түрлі мәнге ие болуы мүмкін немесе шектің болмауы да мүмкін.
Мысалы, егер
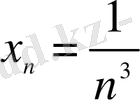 ,
,
 болса, олардың қатынасының
болса, олардың қатынасының
 шегін табу керек.
шегін табу керек.
 ,
,
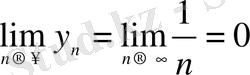 . Сонда
. Сонда
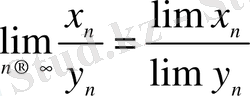 яғни
яғни
 түріндегі анықталмағандық шығады. Бірақ,
түріндегі анықталмағандық шығады. Бірақ,
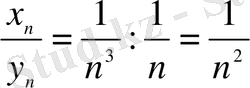 . Демек,
. Демек,
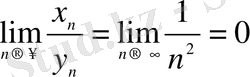 .
.
Ақырсыз аз шамаларды салыстыру. Ақырсыз аз
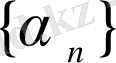 және
және
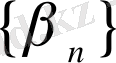 шамалары берілсін
шамалары берілсін
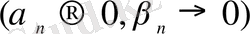 . Осы шамаларды салыстыру денеміз
. Осы шамаларды салыстыру денеміз
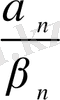 қатнасының шегін табу. Бұл қатынас
қатнасының шегін табу. Бұл қатынас
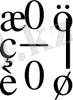 түріндегі анықталмағандық деп аталады.
түріндегі анықталмағандық деп аталады.
Анықтама 5
Егер ақырсыз
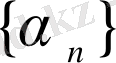 және
және
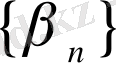 шамалары үшін:
шамалары үшін:
а)
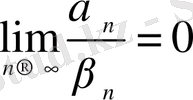 болса, онда
болса, онда
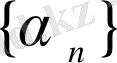 шамасы
шамасы
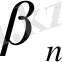 -мен салыстырғанда
жоғарғы ретті ақырсыз аз шама
деп аталады, ал
-мен салыстырғанда
жоғарғы ретті ақырсыз аз шама
деп аталады, ал
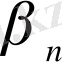 шамасы
шамасы
 -мен салыстырғанда
төменгі ретті ақырсыз аз шама
деп аталады.
-мен салыстырғанда
төменгі ретті ақырсыз аз шама
деп аталады.
б)
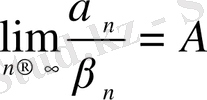 ,
,
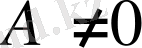 болса, онда
болса, онда
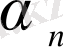 мен
мен
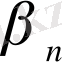 бір ретті ақырсыз аз шамалар
деп аталады.
бір ретті ақырсыз аз шамалар
деп аталады.
в)
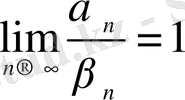 болса, онда
болса, онда
 мен
мен
 эквивалентті
ақырсыз аз шамалар деп аталады.
эквивалентті
ақырсыз аз шамалар деп аталады.
Жиі қолданылатын шектер
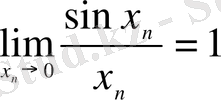 - бірінші тамаша шек.
- бірінші тамаша шек.
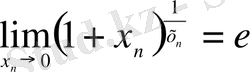 − екінші тамаша шек.
− екінші тамаша шек.
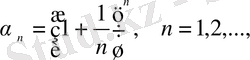 тізбегі үшін
тізбегі үшін
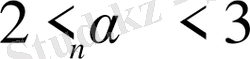 теңсіздігі орындалады. Сондықтан
теңсіздігі орындалады. Сондықтан
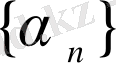 жоғарыдан шенелген өспелі тізбек.
жоғарыдан шенелген өспелі тізбек.
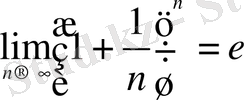
шегі бар болады.
 санының жуық мәні
санының жуық мәні
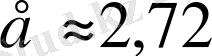 болатыны дәлелденген. Бұл сан Непер саны деп аталады.
болатыны дәлелденген. Бұл сан Непер саны деп аталады.
Тақырып № 3
Функцияның шегі.
 функциясы
функциясы
 нүктесінің манайында (мүмкін сол нүктенің өзінен басқа) анықталсын.
нүктесінің манайында (мүмкін сол нүктенің өзінен басқа) анықталсын.
Анықтама
Егер кішкене
 саны үшін, осы саннан тәуелді
саны үшін, осы саннан тәуелді
 санын
санын
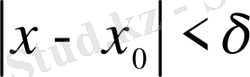 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық
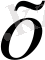 нүктелерінде
нүктелерінде
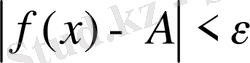 теңсіздігі
теңсіздігі
орындалатындай етіп табуға болса, онда
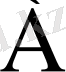 саны
саны
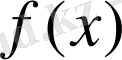 -тің
-тің
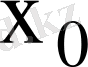 нүктесіндегі шегі деп аталадыда
нүктесіндегі шегі деп аталадыда
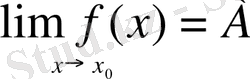 деп белгілінеді. Аталған шек
деп белгілінеді. Аталған шек
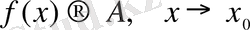 түрінде де жазылады.
түрінде де жазылады.
Мысалы,
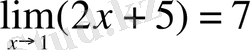 екенін дәлелдейік. Кез келген
екенін дәлелдейік. Кез келген
 саны үшін
саны үшін
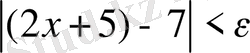 деп алып,
деп алып,
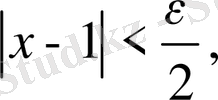 болатынын көреміз. Демек,
болатынын көреміз. Демек,
 Яғни,
Яғни,
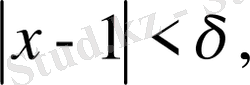 болса,
болса,
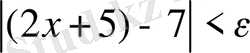 болады.
болады.
Анықтама
Бізге Е жиынындағы сандардан құралған кез келген
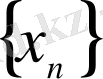 тізбегі, яғни
тізбегі, яғни
 берілсін. Ол тізбек
берілсін. Ол тізбек
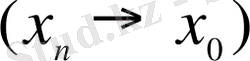
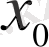 нүктесіне жинақталатын (шегі бар) тізбек болсын, яғни
нүктесіне жинақталатын (шегі бар) тізбек болсын, яғни
 (
(
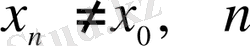 - кез келген натурал сан) . Сонда, егер осы
- кез келген натурал сан) . Сонда, егер осы
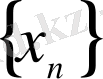 тізбегінің мәндеріне сәйкес берілген функция мәндерінің тізбегі
тізбегінің мәндеріне сәйкес берілген функция мәндерінің тізбегі
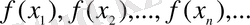 әрқашан да бір А санына жинақталатын болса, онда
әрқашан да бір А санына жинақталатын болса, онда
 функциясы А санына ұмтылады дейді де, А санын
функциясы А санына ұмтылады дейді де, А санын
 функциясының
функциясының
 нүктесіндегі
нүктесіндегі
 шегі деп атайды. Оны былай жазады:
шегі деп атайды. Оны былай жазады:
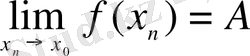 .
.
Бұл екі анықтама эквивалентті анықтамалар.
Шектер туралы теоремалар және оларды шешу тәсілдері :
Теорема 1
 . Қосындының шегі шектердің қосындысына тең.
. Қосындының шегі шектердің қосындысына тең.
Теорема 2
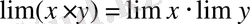 . Көбейтіндінің шегі шектердің көбейтіндісіне тең.
. Көбейтіндінің шегі шектердің көбейтіндісіне тең.
Теорема 3
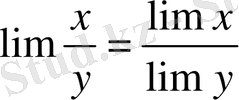 ,
,
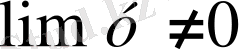 . Егер
. Егер
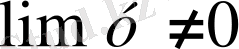 болса, онда бөлшектің шегі алымының шегін бөлімнің шегіне бөлгенге тең.
болса, онда бөлшектің шегі алымының шегін бөлімнің шегіне бөлгенге тең.
Теорема 4
 . Тұрақты шаманың шегі сол шаманың өзіне тең.
. Тұрақты шаманың шегі сол шаманың өзіне тең.
Теорема 5
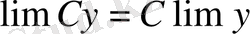 . Тұрақты шаманы шектің сыртына шығаруға болады.
. Тұрақты шаманы шектің сыртына шығаруға болады.
Шектерді есептеу мысалдар:
Мысал 1 Шек астындағы бөлшекті (х-2) -ге қысқартып
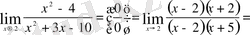
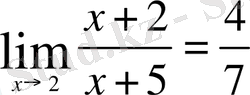
Мысал 2
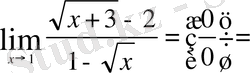
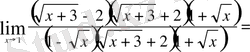
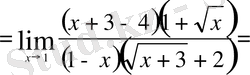
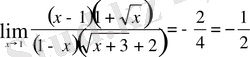
Мысал 3
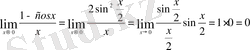
Мұндағы
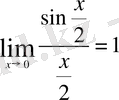 (бірінші тамаша шек)
(бірінші тамаша шек)
Мысал 4
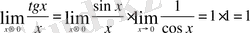
Бесінші және алтыншы мысалдардағы шектер бізге белгілі
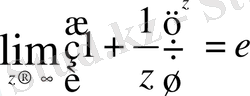 немесе
немесе
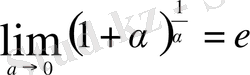 (екінші тамаша шек) теңсіздіктерін қолдану арқылы есептеледі.
(екінші тамаша шек) теңсіздіктерін қолдану арқылы есептеледі.
Мысал 5
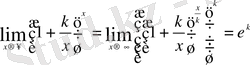
Мысал 6

Ескерту
:
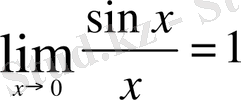 шегі
шегі
 анықталмағандығын, ал
анықталмағандығын, ал
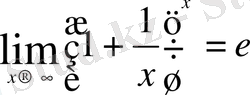 және
және
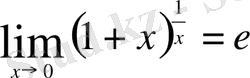 шектері
шектері
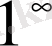 анықталмағандығын айқындайды.
анықталмағандығын айқындайды.
Анықтама
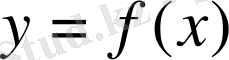 функциясының
функциясының
 болып
х
-тің
болып
х
-тің
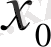 -ге ұмтылғандағы
-ге ұмтылғандағы
 -ге тең шегі осы функцияның
сол жақты шегі
деп аталады да
-ге тең шегі осы функцияның
сол жақты шегі
деп аталады да
 деп белгіленеді, ал
деп белгіленеді, ал
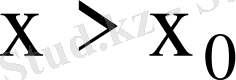 болып
х
-тің
болып
х
-тің
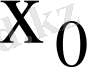 -ге ұмтылғандығы
-ге ұмтылғандығы
 -ге тең шегі функцияның
оң
жақты шегі
деп аталады да,
-ге тең шегі функцияның
оң
жақты шегі
деп аталады да,
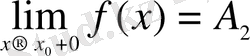 деп белгіленеді.
деп белгіленеді.
Егер
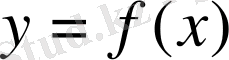 функциясы
функциясы
 нүктесінде және осы нүктенің маңайында анықталып,
нүктесінде және осы нүктенің маңайында анықталып,
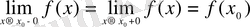 теңдігі орындалса, онда
теңдігі орындалса, онда
 функциясы
функциясы
 нүктесінде үзіліссіз болады.
нүктесінде үзіліссіз болады.
Егер осы екі теңдіктің ең кемінде біреуі орындалмаса, онда
 үзіліс нүктесі деп аталады. Үзілістің екі түрі бар:
үзіліс нүктесі деп аталады. Үзілістің екі түрі бар:
1. Секірме үзіліс, егер
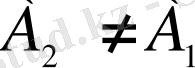 болып
болып
 немесе
немесе
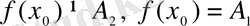 немесе
немесе
 нүктесінде
нүктесінде
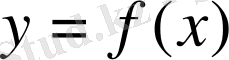 анықталмаса.
анықталмаса.
2. Шексіз үзіліс.
Мысал 1
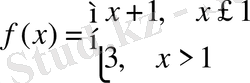 функциясы үшін
функциясы үшін
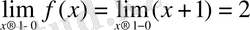
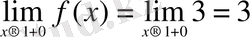
теңдіктері орындалады, демек
 - секірме үзіліс нүктесі; секіріс
- секірме үзіліс нүктесі; секіріс
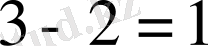 -ге тең.
-ге тең.
У
3
2
1
-1 0 1 х
Сурет 1.
Мысал 2
 функциясын
функциясын
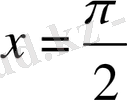 нүктесінде функцияны үзіліссіздікке зерттейік.
нүктесінде функцияны үзіліссіздікке зерттейік.
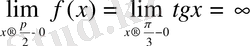

теңдіктері орындалады, демек
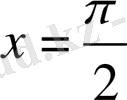 шексіз үзіліс нүктесі. (Сурет-2)
шексіз үзіліс нүктесі. (Сурет-2)
у
0 π х
Сурет 2.
Тақырып № 5
Функцияның нүктедегі туындысы мен дифференциалы
8. 1 Туындының анықтамасы. Туындының механикалық мағынасы.
8. 2 Туындының геометриялық мағынасы
8. 3 Функцияның дифференциалдануы
8. 4 Функцияның дифференциалы
8. 5 Жоғары ретті туындылар мен дифференциалдар. Лейбниц формуласы.
8. 6 Дифференциалданатын функциялардың негізгі теоремалары. Лопиталь ережесі.
8. 7 Туынды арқылы функцияның зерттеу.
5. 1 Туындының анықтамасы. Туындының механикалық мағынасы.
Түзу сызықты қозғалыстың жылдамдығын қарастырайық. Дене түзу сызық бойымен және
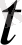 уақыт ішінде
уақыт ішінде
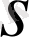 жолын жүрсін, яғни
жолын жүрсін, яғни
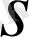 қашықтық
қашықтық
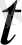 уақыттың функциясы берілсін:
уақыттың функциясы берілсін:
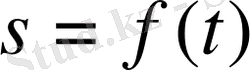 . Бұл қозғалыс теңдеуі.
. Бұл қозғалыс теңдеуі.
Дене қозғалысын уақыттың
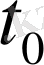 мезгілінен
мезгілінен
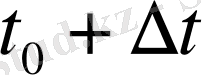 мезгіліне дейін, яғни
мезгіліне дейін, яғни
 интервалында қарастырамыз. Дене
интервалында қарастырамыз. Дене
 уақытта
уақытта
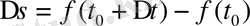 жол жүреді.
жол жүреді.
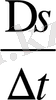 қатынасын дене қозғалысының
қатынасын дене қозғалысының
 уақыты ішіндегі
орта жылдамдығы
деп аталады және белгілеуі:
уақыты ішіндегі
орта жылдамдығы
деп аталады және белгілеуі:
 .
.
Шекке көшеміз:
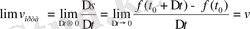 .
.
Анықтама.
Жол өсімшесінің уақыт өсімшесіне қатынасының уақыт өсімшесі нөльге ұмтылғандағы шегі:
 теңдігімен анықталатын
теңдігімен анықталатын
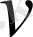 шамасын дене қозғалысының
шамасын дене қозғалысының
 мезгіліндегі
лездік жылдамдығы
деп аталады.
мезгіліндегі
лездік жылдамдығы
деп аталады.
Айталық,
 аралығында
аралығында
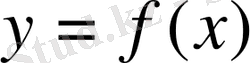 функциясы анықталсын. Бұл аралықтан
функциясы анықталсын. Бұл аралықтан
 нүктесін алып, оған
нүктесін алып, оған
 өсімшесін берейік. Сонда
өсімшесін берейік. Сонда
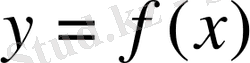 функциясы да өсімше қабылдайды:
функциясы да өсімше қабылдайды:
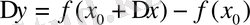 , мұнда
, мұнда
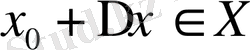 .
.
Анықтама.
Егер
 нөльге ұмтылғанда функция өсімшесі мен аргумент өсімшесі қатынасының шегі бар болса, онда бұл шек берілген функцияның
нөльге ұмтылғанда функция өсімшесі мен аргумент өсімшесі қатынасының шегі бар болса, онда бұл шек берілген функцияның
 нүктесіндегі
туындысы
деп аталады:
нүктесіндегі
туындысы
деп аталады:
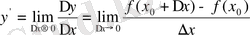 .
.
Туындыны табу амалын функцияны дифференциалдау деп атайды. Жоғарыда қарастырылған физикалық есепте айнымалы жылдамдық жүрген жолдың туындысына тең:
 . Бұл есеп туындының механикалық мағынасын анықтайды.
. Бұл есеп туындының механикалық мағынасын анықтайды.
5. 2 Туындының геометриялық мағынасы
 қисық сызықтың бойынан екі нүкте
қисық сызықтың бойынан екі нүкте
 және
және
 алайық және сол нүктелер арқылы қиюшы жүргізейік.
алайық және сол нүктелер арқылы қиюшы жүргізейік.
 нүктесін қозғалмайды деп есептеп,
нүктесін қозғалмайды деп есептеп,
 нүктесін
нүктесін
 қисығы бойымен
қисығы бойымен
 нүктесіне дейін жүргізейік. Егер
нүктесіне дейін жүргізейік. Егер
 , онда
, онда
 түзуі
түзуі
 -ға ұмтылады.
-ға ұмтылады.
Анықтама.
 нүктесі
нүктесі
 нүктесіне ұмтылғанда қиюшы
нүктесіне ұмтылғанда қиюшы
 мен түзу
мен түзу
 арасындағы
арасындағы
 бұрыш нөльге ұмтылса, онда
бұрыш нөльге ұмтылса, онда
 түзуін
түзуін
 қисық сызықтың
қисық сызықтың
 нүктесіндегі
жанамасы
деп атайды.
нүктесіндегі
жанамасы
деп атайды.
Айталық,
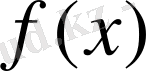 -тың
-тың
 нүктесіндегі туындысы
нүктесіндегі туындысы
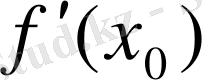 . Қиюшы
. Қиюшы

 осімен
осімен
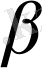 бұрыш жасайды. Сонда
бұрыш жасайды. Сонда
 немесе
немесе
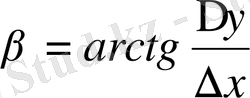 . Егер
. Егер
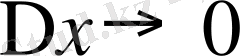 , онда
, онда
1)
 ;
;
2)
 ;
;
3)
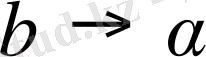 , онда
, онда
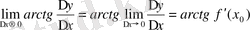 .
.
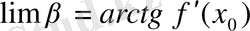 , онда
, онда
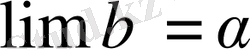



 .
.
Сонымен, туынды
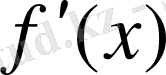
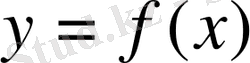 функцияның
функцияның
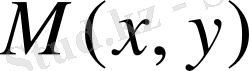 нүктесіне жүргізілген жанама мен
нүктесіне жүргізілген жанама мен
 осінің оң бағытының арасындағы бұрыштың тангенсін кескіндейді.
осінің оң бағытының арасындағы бұрыштың тангенсін кескіндейді.
Онда жанаманың теңдеуі:
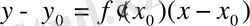 .
.
Осы нүктедегі жанамаға перпендикуляр түзуді
нормаль түзу
деп атайды; оның теңдеуі:
 .
.
5. 3 Функцияның дифференциалдануы
Функцияның туындысын табу амалын дифференциалдау деп, ал туындысы бар функцияны дифференциалданатын функция деп атайды.
Егер
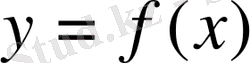 функциясының
функциясының
 нүктесінде туындысы бар болса, онда
нүктесінде туындысы бар болса, онда
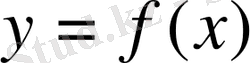 функциясы осы нүктеде үздіксіз болады, ал үзіліс функцияның
функциясы осы нүктеде үздіксіз болады, ал үзіліс функцияның
 нүктеде туындысы болмайды.
нүктеде туындысы болмайды.
Арифметикалық амалдардың дифференциалдау ережелері:
Айталық,,
 және
және
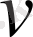 үздіксіз функциялары берілсін. Екі функцияның алгебралық қосындысының, көбейтіндісінің және қатынасының туындылары бар болады да мына формулалар бойынша табылады:
үздіксіз функциялары берілсін. Екі функцияның алгебралық қосындысының, көбейтіндісінің және қатынасының туындылары бар болады да мына формулалар бойынша табылады:
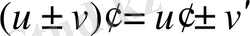 ;
;
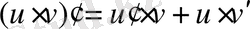 ;
;
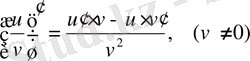
Егер көбейтіндіде көбейткіштің біреуі тұрақты шама болса, онда
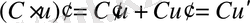 , өйткені тұрақты шаманың туындысы нөльге тең.
, өйткені тұрақты шаманың туындысы нөльге тең.
Күрделі функцияның дифференциалдануы:
Егер
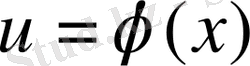 функциясының
функциясының
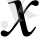 нүктесінде, ал
нүктесінде, ал
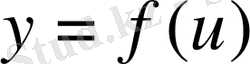 функциясының сол
функциясының сол
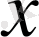 -ке сәйкес
-ке сәйкес
 нүктесінде туындылары бар болса, онда сол
нүктесінде туындылары бар болса, онда сол
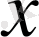 нүктесінде күрделі
нүктесінде күрделі
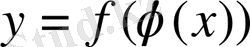 функциясының да туындысы бар болады және мынаған тең:
функциясының да туындысы бар болады және мынаған тең:
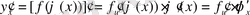 .
.
Мысалы:

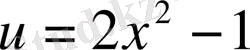

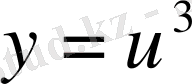
 .
.
Кері функцияның дифференциалдануы:
Егер
 функциясының
функциясының
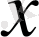 нүктесінде нөльге тең емес
нүктесінде нөльге тең емес
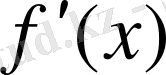 туындысы бар болса, онда сол
туындысы бар болса, онда сол
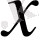 -ке сәйкес
-ке сәйкес
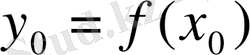 нүктесінде щған кері
нүктесінде щған кері
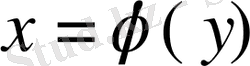 функциясының туындысы бар болады және
функциясының туындысы бар болады және
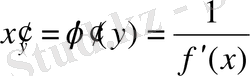 .
.
Мысалы:
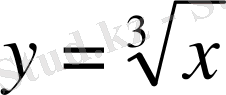 . Осы функцияға кері функция:
. Осы функцияға кері функция:
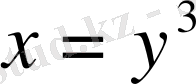 және
және
 . Олай болса,
. Олай болса,
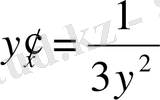 .
.
Дәрежелік функцияның туындысы:
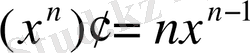 .
.
Тригонометриялық функциялардың туындысы:
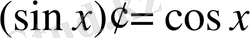 ;
;
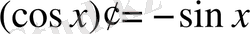 ;
;
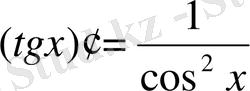 ;
;
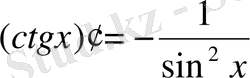
Кері тригонометриялық функциялардың туындысы:
 ;
;
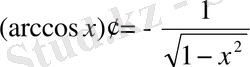 ;
;
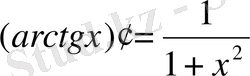 ;
;
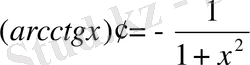
Логарифмдік және көрсеткіштік функциялардың туындылары:
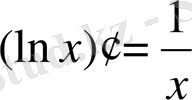 ;
;
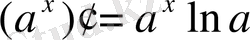 ;
;
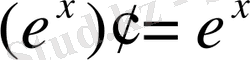
Логарифмдік дифференциалдау тәсілі:
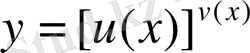 көрсеткішті-дәрежелік функцияның туындысын анықтайық. Ол үшін берілген функцияны логарифмдеп, содан кейін логарифмдеу нәтижесінде шыққан функцияға дифференциалдау ережелерін қолданамыз.
көрсеткішті-дәрежелік функцияның туындысын анықтайық. Ол үшін берілген функцияны логарифмдеп, содан кейін логарифмдеу нәтижесінде шыққан функцияға дифференциалдау ережелерін қолданамыз.
Сонымен
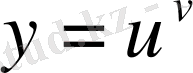 функциясын логарифмдесек
функциясын логарифмдесек
 болады. Осы өрнектен күрделі функцияның туындысының формуласы бойынша:
болады. Осы өрнектен күрделі функцияның туындысының формуласы бойынша:
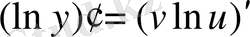 ;
;
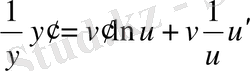 ;
;
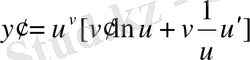 ;
;
Мысалы:
 функциясының туындысын табу керек.
функциясының туындысын табу керек.
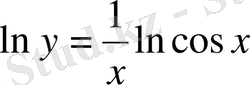 ,
,
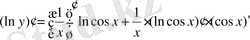
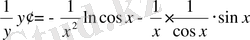 ,
,
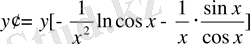
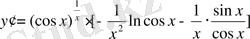 .
.
Айқындалмаған функциялардың туындылары:
Айталық,

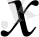 -тің айқындалмаған функциясы, яғни
-тің айқындалмаған функциясы, яғни
 тәуелсіз айнымалыны
тәуелсіз айнымалыны
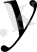 функциясымен байланыстыратын,
функциясымен байланыстыратын,
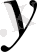 -ке қатысты шешілмейтін, қандай да бір теңдеу арқылы беріледі. Онда
-ке қатысты шешілмейтін, қандай да бір теңдеу арқылы беріледі. Онда
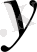 функциясы
функциясы
 -тен тәуелді екенін есепке ала тұра, бұл теңдеуді
-тен тәуелді екенін есепке ала тұра, бұл теңдеуді
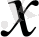 бойынша дифференциалдаймыз.
бойынша дифференциалдаймыз.
Мысалы:
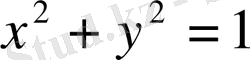 теңдеуімен берілген
теңдеуімен берілген
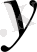 функциясының туындысын табу керек.
функциясының туындысын табу керек.
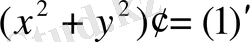 ,
,
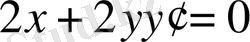 ,
,
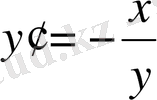 .
.
Параметр арқылы берілген функцияның туындысы:
Айталық, функция
 -тің аргументі
-тің аргументі
 -тен тәуелділігі параметр
-тен тәуелділігі параметр
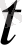 арқылы берілсін:
арқылы берілсін:
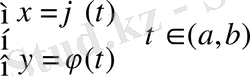 және
және
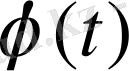 ,
,
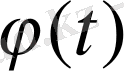 функциялардың туындылары бар болсын. Бұл тәуелділікті былай түсінуге болады: егер
функциялардың туындылары бар болсын. Бұл тәуелділікті былай түсінуге болады: егер
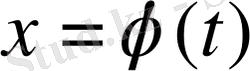 функцияның кері функциясы
функцияның кері функциясы
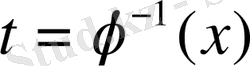 бар болса және
бар болса және
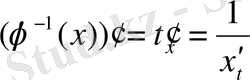 , онда бір формуладан тұратын теңдікке келуге болады:
, онда бір формуладан тұратын теңдікке келуге болады:
 . Енді күрделі функцияны дифференциалдау ережесін пайдаланамыз:
. Енді күрделі функцияны дифференциалдау ережесін пайдаланамыз:
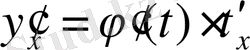 . Осыдан
. Осыдан
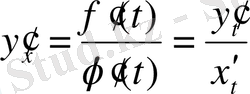 .
.
Екінші ретті туынды:
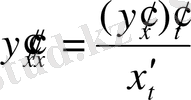 және үшінші ретті туынды:
және үшінші ретті туынды:
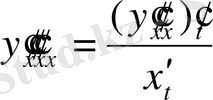 .
.
5. 4 Функцияның дифференциалы
Айталық,
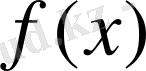 функциясының шектелген туындысы бар болсын, онда
функциясының шектелген туындысы бар болсын, онда
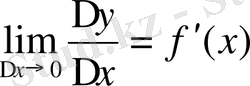 , демек
, демек
 ,
,
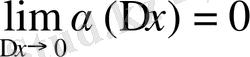 ,
,
 - шексіз аз шама.
- шексіз аз шама.
Онда функцияның өсімшесі:
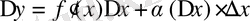 . Осы теңдікте екінші қосылғыш жоғары ретті шексіз аз шама болғандықтан, бірінші қосылғыш функция өсімшесіне эквивалентті болады.
. Осы теңдікте екінші қосылғыш жоғары ретті шексіз аз шама болғандықтан, бірінші қосылғыш функция өсімшесіне эквивалентті болады.
Анықтама.
Функцияның туындысы мен аргумент өсімшесінің көбейтіндісі
дифференциал
деп аталады және мына түрде жазады:
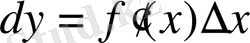 .
.
Онда жоғарыда берілген теңдіктің бірінші қосылғышы дифференциал болады. Дербес жағдайда, егер
 болса, онда
болса, онда
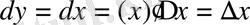 , яғни
, яғни
 және осыны пайдаланып дифференциалдың формуласын келесі түрде жазуға болады:
және осыны пайдаланып дифференциалдың формуласын келесі түрде жазуға болады:
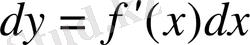 .
.
Осыдан
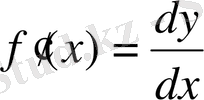 , яғни туынды функция дифференциалының аргумент дифференциалына бөлінген мәніне тең.
, яғни туынды функция дифференциалының аргумент дифференциалына бөлінген мәніне тең.
Дифференциалдың қасиеттері:
Негізігі элементар функциялардың туындыларын біле тұрып, біз еш қиындықсыз осы функциялардың дифференциалдарының кестесін құрастыра аламыз.
Айталық,
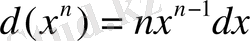 ,
,
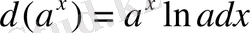 , т. с. с.
, т. с. с.
Арифметикалық амалдар нәтижелерінің дифференциалдары:
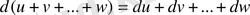 ;
;
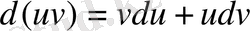 ;
;
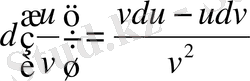 .
.
Күрделі функцияның дифференциалы:
Айталық,
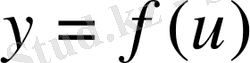 және
және
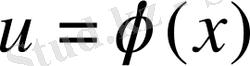 - үзіліссіз функциялар және олардың туынддылары:
- үзіліссіз функциялар және олардың туынддылары:
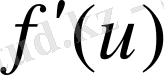 ,
,
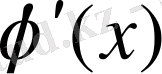 . Егер
. Егер
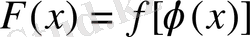 белгілесек, онда
белгілесек, онда
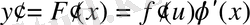 . Екі жағын
. Екі жағын
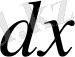 -ке көбейтеміз:
-ке көбейтеміз:
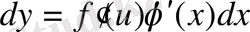 , ал
, ал
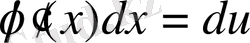 , олай болса,
, олай болса,
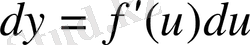 .
.
Функцияның дифференциалдануы.
Анықтама.
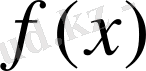 функциясы
функциясы
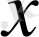 нүктесінде дифференциалданады, егер оның осы нүктеде дифференциалы болса.
нүктесінде дифференциалданады, егер оның осы нүктеде дифференциалы болса.
Егер
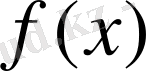 функциясы дифференциалданатын болса, онда ол міндетті түрде үзіліссіз болады.
функциясы дифференциалданатын болса, онда ол міндетті түрде үзіліссіз болады.
Дифференциалды жуықтап есептеулерге пайдалану.
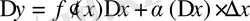
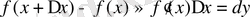
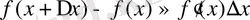 . Соңғы жуықталған теңдік ең алдымен тәжірибелік тұрғыдан қарағанда келесі есепті шешу үшін қолданады:
. Соңғы жуықталған теңдік ең алдымен тәжірибелік тұрғыдан қарағанда келесі есепті шешу үшін қолданады:
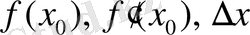 мәндері белгілі;
мәндері белгілі;
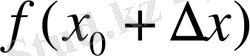 -тің жуық мәнін есептеу керек. Сонда төменгі формула анықталады:
-тің жуық мәнін есептеу керек. Сонда төменгі формула анықталады:
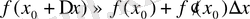 .
.
Мысалы:
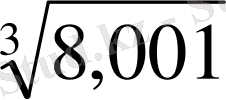 мәнін табу керек:
мәнін табу керек:
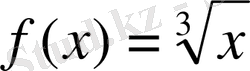 ,
,
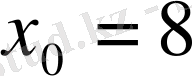 ,
,
 , демек
, демек
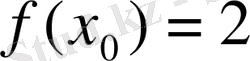 . Ал
. Ал
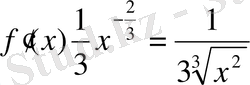 ,
,
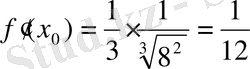 . Сонда
. Сонда
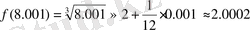 .
.
5. 5 Жоғары ретті туындылар мен дифференциалдар. Лейбниц формуласы.
Егер
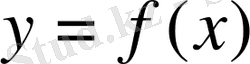 функциясының туындысы бар болса, онда оны
функциясының туындысы бар болса, онда оны
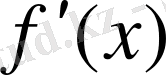 деп белгілеп, бірінші ретті туынды деп атаймыз. Осы 1-ші ретті туындыны бөлек функция деп қарастырайық, онда оның туындысы бар болуы мүмкін және
деп белгілеп, бірінші ретті туынды деп атаймыз. Осы 1-ші ретті туындыны бөлек функция деп қарастырайық, онда оның туындысы бар болуы мүмкін және
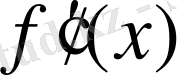 екінші ретті туынды деп аталады. Сол сияқты функцияның
екінші ретті туынды деп аталады. Сол сияқты функцияның
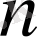 -ші ретті туындысын жазуға болады:
-ші ретті туындысын жазуға болады:
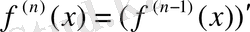 немесе
немесе
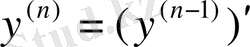 .
.
Мысалдар:
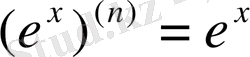
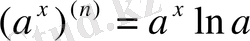
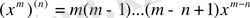
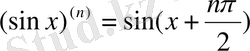
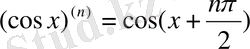 .
.
Егер
 және
және
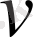 дифференциалданатын функциялар болса, онда сызықты комбинация үшін келесі формула орынды:
дифференциалданатын функциялар болса, онда сызықты комбинация үшін келесі формула орынды:
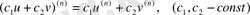 , ал олардың көбейтіндісі үшін:
, ал олардың көбейтіндісі үшін:

Бұл формула Лейбниц формуласы деп аталады.
Мұнда
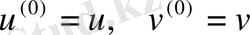 ;
;
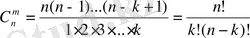 - бином коэффициенттері.
- бином коэффициенттері.
Жоғары ретті дифференциалдар
Функцияның бірінші ретті дифференциалы келесі формуламен анықталады:
 , ал екінші ретті дифференциалы:
, ал екінші ретті дифференциалы:
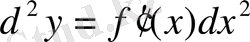 ,
,
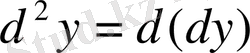 .
.
Сол сияқты
 -ші ретті дифференциал мына формуламен анықталады:
-ші ретті дифференциал мына формуламен анықталады:
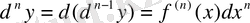 . Бұл формуладан:
. Бұл формуладан:
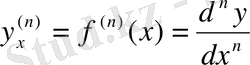
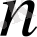 -ші ретті туынды шығады.
-ші ретті туынды шығады.
Тақырып № 6
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz