Сыртқы бөлімнің бірінші курс студенттері үшін математикадан бақылау жұмысының әдістемелік нұсқаулығы


Математикадан бақылау жұмысын орындау туралы жалпы бақылау
Математикадан бақылау жұмысының негізгі мақсаты- математика курсындағы бастауыш сынып мұғаліміне қажетті білімдерді игеру саласын анықтау. Бақылау жұмысын орындау арқылы сыртқы бөлім студенті өзбетінше тапсырмаларды дұрыс ұйымдастыра білуге үйренеді, біліміндегі кемшіліктерін анықтауға және оны жоюға мүмкіндік алады.
Сыртқы бөлім студенттері оқу мерзімі бес жыл болуына байланысты әр жылда бір бақылау жұмысын орындайды. Әрбір бақылау жұмысы сол курста өтілетін бөлімдерге қатысты есептерді ғана қамтиды.
Бақылау жұмысын орыңдауға кіріспес бұрын студент берілген тапсырмаларды орындауға қажетті теориялық материалды оқып білуі керек. Мұнда әр курстағы тапсырмаларды орыңдау үшін студент білуге тиіс талаптар көрсетілген. Сол талаптарды орындау арқылы ғана берілген есептерді дұрыс шығаруға болады. Егер де теориялық материалдарды оқып-меңгеріп есептерді шығару барысында студент қиындықтарға кездессе, онда кеңесті пән мүғалімінен алуына болады.
Студент өз бетінше берілген тапсырмаларды орындаса, онда оған «есептелінді» қойылады. Ал, студент тапсырмаларды орындауда қателіктер жіберетін болса, онда ол курстағы негізгі сұрақтарды игермегендігін көрсетеді және жұмыс есептелінбейді де, қайта дұрыс шығарып сәйкесінде өзгерістер енгізілген соң қосымша әңгіме өткізіледі.
Ұсынылып отырған бақылау жұмыстары бірнеше тақырыптан тұрады. Әр тақырыпта 10 тапсырмадан тұрады. Студент өз сынақ кітапшасындағы көрсетілген ең соңғы цифрына қарап тиісті нұсқасын жазып алады.
Мысалы, сынақ кітапшасының соңғы цифры 5 болса, онда ол 5-ші.
Нұсқа және мынадай есептерді орындайды: 1. 5, 2. 5, 3. 5, 4. 5, 5. 5, 6. 5, 7. 5, 8. 5, 9. 5, 10. 5.
- Әрбір есеп жеке параққа шығарылуы тиіс.
- Тапсырманы нұсқауда берілген ретпен орындау керек.
- Есептердің шарты дәптерге көшіріп алып, әрбір орындалған тапсырмаға қысқаша түсініктеме беріп отыру қажет.
- Бақылау тапсырмалары қатесіз орындалуы шарт. Қажетті сызбалар қаламның көмегімен жүргізіледі.
Бақылау жұмысын орындау үшін студент мынадай әдебиеттерді қолданылуына болады.
1. Л. П. Стойлова, АМ. Пышкало "Основы начального курса математики" М, Просвещение 1988.
2. Н. Я. Виленкин, А. М. Пышкал и др. "Математака" Прос. 1977. 3. Б. М. Архипов, М. П. Лельчук и др. "Математика" Минск. 1976. 4. А. А. Столер, М. П. Лельчук и др. "Математика" Минск. 1975. 5. Алиева. К. С. "Математика" Шымкент. 2000.
6. Оспанов. Т. Қ. "Математика" Алматы. 2000.
7. Виленкин. Н. Я. "Задачник-практикум по математике"
М., Прос., 1977.
8. Пышкало. А. М., Стойлова Л. П. Даврова Н. Н., Ирошников Г. А.
"Сборник задач по математике "М., "Просвещение", 1979
1-курс Бірінші курсқа арналған бақылау жұмысының тақырыптары
Бірінші курсқа арналған бақылау жұмысының тақырыптары төмендегіше:
1. Жиын ұғымы. Жиын элементі.
2. Жиынның берілу тәсілдері.
3. Жиыңдардың графикалық иллюстрациясы (сипаттамасы) .
4. Жиындарға амалдар қолдану.
5. Жиындардың декарттық көбейтіндісі.
6. Жиындарды өзара қиылыспайтын ішкі жиындарға бөлу.
7. Пікір ұғымы.
8. Предикат.
9. Кванторлар.
10. Комбинаторка элементтері.
Студент әр тақырыпта берілген тапсырмадан барлығы 10 есеп шығаруы тиіс. Есепті шығармас бұрын студент мына мәселелерді білуге тиіс.
- жиын ұғымы мен оның элементтері;
- жиынның түрлері мен жиынның берілу тәсілдері;
- бос жиын мен ішкі жиын және тең жиыңдар;
- жиындардың қиылысуы, бірігуі және айырымы;
- жиынның толықтауышы;
- жиындардың декарттық көбейтіндісі;
- жиындарды өзара қиылыспайтын ішкі жиыңдарға жіктеу;
- пікір ұғымы мен қарапайым және құрама пікірлер;
-пікірлердін дезъюнкциясы, конъюнциясы, импликациясы және
эквиваленциясы;
- предикат, предикаттың терістемесі;
- предикаттың конъюнкциясы, дезъюнкциясы және импликациясы;
- кванторлар мен комбинаторикалық есептер;
Бакылау жұмысын орындау үшін студентте төмеңдегідей біліктіліктер болуы қажет:
- жиындар арасындағы қатынастарды (қиылысуы, бірігуі, айырымы, тең жиындар) Әйлер дөңгелекшелерінің көмегімен кескіндеу:
- тиісінше анықтамаларға сүйене отырып "а" элементінің А U В, АВ, АВ және А\В- жиындарына тиісті немесе-тиісті емес екендігін тұжырымдау;
- бір немесе бірнеше қасиеттердің негізіңде жиындарды кластарға жіктеу;
- екі сандық жиындардың декарттың көбейтіндісін декарттық координаталар жүйесіңде кескіндеу;
- құрама пікірлердің ақиқаттығын анықтау;
- пікірлердің конъюнкциясы мен дезъюнкциясының терістемесін құру
- кванторлар арқылы жазылған сөйлемдерді оқу;
- комбинаторика элементтерін қолданып есептер шығару;
Тапсырмалардың орындалу үлгілері
І-тапсырма
"Студенттер,, сөзіне тиісті әріптер жиының элементтерін атап шығу арқылы анықтау қажет.
Берілген сөз бірнеше әріптен тұрады және кейбір әріптер бірнеше рет кездеседі. Сондықтан, жиынды оның барлық элементтерін атап шығу арқылы берілу тәсілін қолданып және жиындағы әрбір элементтің қайталанбайтындығын ескере отырып «студенттер» сөзіне тиісті әріптер жиынын төмендегідей жазуға болады:{ с, т, у, д, е, н, р}
2- тапсырма
А={ х / хN, -3< х < 5} жиының элементгерін тауып, оның барлық элементтерін атап шығу арқылы жазыңдар.
Жиынды оның барлық элементтерін атап шығу арқылы жазу үшін алдымен бұл жиынның элементтерінің хеN- натурал сандарға тиісті екеңдігін ескеруіміз қажет. Ал натурал сандар дегеніміз 1, 2, 3, 4, 5, 6 . . . элементтерінен тұрады. Сонымен қатар берілген жиынның элементтері -3<х<5 теңсіздігін , яғни -3-тен үлкен, және 5-тен кіші немесе тең болғандықтан осы аралықтағы бүтін сандарды жеке-жеке атап шығамыз. Олар: -2, -1, 0, 1, 2, 3, 4, 5. Бұл сандардың барлығы бірдей натурал сандарға жатпайды. Тек қана 1, 2, 3, 4, 5 сандары ғана натурал сан. Сол себепті бастапқы берілген А жиынның барлық элементтерін атап шығу арқылы жазсақ
А={1, 2, 3, 4, 5} болады.
3-тапсырма
А-бір таңбалы жұп сандар жиыны, ал В-натурал сандар жиыны. Осы жиындарды Эйлер-Венн диаграммалары арқылы кескіндеңіздер. Есептің шарты бойынша А-жиыны бір таңбалы жұп сандар жиыны, яғни 2, 4, 6, 8-сандарынан тұрады. Ал, В-жиыны натурал саңдар жиыны болғандықтан В={1, 2, 3, 4, 5, 6 . . . } Осы екі жиында да 2, 4, 6, 8 сандары кездеседі. Сонымен қатар бұл А-жиынының бүкіл барлық элементтері В-жиынына да тиісті. Демек, А жиынының әрбір элементі болып тұр. Сондықтан А В немесе А жиыны В жиынының ішкі жиыны. Енді жиындардың ара қатынастарын көрнекті кескіндеу үшін кез-келген жиынның элементтерін тұйық контур ішінде орналасқан нүктелер ретінде қарастыруға болатаңдығын ескерсек және осылайша графиктік кескіндеу әдісін Эйлер-Венн диаграммасы деп атайтындықтан есептің шартыңда берілген тапсырманы төмендегідей кескіндейміз.
4-тапсырма
А={1, 2, 3, 4, 5, 6}, В={6, 7, 11, 5, 8, 9, 4, 10, 12} жиындарының АВ, АВ және А\В тауып, жауабын жиынның берілуінің екінші тәсілімен жазыңыздар. Ажәне В жиындарының қиылысуы дегеніміз А және В жиындарының екеуіне де тиісті элементтерден және тек қана сол элементтерден тұратын жиынды айтатындықтан АВ={4, 5, 6} болады. Себебі 3, 5, 10 саңдары екі жиынға да тиісті. А және В жиындарының бірігуі деп не А не В жиындарының ең болмағанда біреуіне тиісі элементтерден және тек ғана сол элементтерден тұратын жиыңды айтамыз. Олай болса АU АU В={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 }.
А және В жиындарының айырмасы деп А жиынына тиісті жене В жиынына тиісті емес элементгерден және тек қана сол элементтерден тұратын жиын болғандықтан А\В-{ 1, 2, 3} болады.
Енді жиындардың қиылысуын, бірігуін және айырымын жиынның берілуінің екінші тәсілімен жазамыз, яғни жиынды оны құрайтын элементтердің сипаттамалық қасиетін атау арқылы анықтаймыз. Сонда: А В={х/х+еN, 3< х < 6}, ал А В={х/хеN, х < 12} және А\ В={х/хеN, х < 3}.
5 тапсырма
А={3, 6, 9, 12} және В={у/уеz, -3<у<3} жиындарының декарттық көбейтіндісін тауып, графигін координаталар жүйесінде кескіндеңіздер.
Жиындардың декарттық көбейтіндісі деп бірінші компоненті А жиынынан, ал екінші компоненті В жиынынан алынған жұптардың жиынын айтатын болғандықтан бізге алдымен осылайша қурылған жұптар қажет. Алдымен В жиынын жиындардың берілуінің бірінші тәсілімен жазып аламыз. Яғни В={-3, -2, -1, 0, 1; 2} себебі В-жиынының элементтері -3<у<3 аралығындағы бүтін сандар. Енді жұптарды құруға болады, мұнда АхВ={(х, у) /хеА және у^В} болуға тиіс. Сонымен
АхВ={(3, -3), (3, -2), (3, -1), (3, 0), (3, 1), (3, 2), (6, -3), (6, -2), (6, -1), (6, 0), (6, 1), (6, 2), (9, -3), (9, -2), (9, -1), (9, 0), (9, 1), (9, 2), (12, -3), (12, -2), (12, -1), (12, 0), (12, 1), (12, 2) } оның графигі төмендегідей ( 2-сурет)
А- барлық үшбұрыштар жиынын өзара қиылыспайтын ішкі жиындарға бөлу үшін ішкі жиындар өзара қиылыспауы тиіс, ішкі жиындардың бірігу жиыны бастапқы берілген А жиынымен тең болады және ол ішкі жиындар бос жиын болмауы керек. Соңдықтан А1- жиыны барлық сүйір бұрышты үшбұрыштар, А2-жиыны барлық доғал бұрышты үшбұрыштар және АЗ- барлық тік бұрышты ұшбұрыштардың жиыны болады. Өйткені жоғарыдағы айтылған шарттар толығымен орындалады:
1) А1≠0, А2≠0, А3≠0
2) А, А 2 =0, А г А 3 =0 ; А 2 А 3 =0
3) А1 А2 АЗ =А
7-тапсырма
(АVВ) =>С өрнегінің шындық қатесін құрыңыз. Бұл өрнектің шындық қатесін құрмас бұрын АVВ танбасы арқылы А және В пікірлерінің дизьюнкциясы ал А мен В пікірлерінің импликациясы белгіленетінін, ал А мен В - осы пікірлердің терістемесі, яғни пікір ақиқат болғанда жалған немесе жалған болғада ақиқат пікірді айтылатынын ескеруіміз қажет. Сонымен қатар А, В және С пікірлері үшін 8 түрлі жағдайда "ақиқат" және "жалған" ұғымдарын қарастырамыз. Нәтижеде төмендегідей кесте аламыз:
8-тапсырма
X ={1, 2, 3, 4, . . . , 20}жиынында А(х) :"х-2-ге еселі", В(х) :"х-жұп сан "деген предикаттар берілген. А(х) В(х) предикатының шындық жиынын табыңыздар.
Есептің шарты бойынша В(х) ={2, 4„6. 8, 10, 12, 14, 16, 18, 20} ал А(х) ={2, 4„6, 8, 10, 12, 14, 16, 18, 20}. Сондықтан А(х) ^В(х) конъюнкдиясы бұл пікірлердің екеуіде ақиқат болғанда, тек сонда ғана ақиқат болатын пікір болғандықтан осы жиындардың қиылысуы предикаттардың шындық жиыны болып табылады. Сонымен:
А(х) ^В(х) ={2, 4, 6, 8, 10, 12, 14, 16, 18, 20}.
9-тапсырма
V(хеR) 2х-5=3х пікірін оқып оның шындық немесе жалған екеңдігін анықтаңыздар. Мұнда V символы " барлық,, " әрбір,, " кез-келген„" әр түрлі,, сөздерінің орнына пайдаланатын жалпылық кванторы ал хеR дегеніміз х-тің нақты сандар орнына тиісті екенін көрсетеді. Сондықтан бұл пікір төмендегідей оқылады:
- нақты сандар жиынынан алынған кез-келген х-үшін 2х-5=3х болады. Бұл жалған пікір, себебі кез-келген нақты саңды 2х-5=3х теңдігіндегі айнымалы х-тің орнына апарып қойғанымен тендік орындалмайды.
10-тарсырма
С -терулер санын есептеңіздер.
Берілген жиынның m элементінен таңдап алынған әр түрлі R элементтен R-ден жасалған қайталаусыз терулер деп атап,
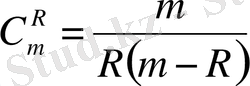 формуласы бойынша есептейді. Біздің жағдайымызда m=7, R=5 бұдан
формуласы бойынша есептейді. Біздің жағдайымызда m=7, R=5 бұдан
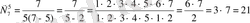
Таңырып-6. Бейнелеу
6. 1. А-сіздің топтағы студенттер жиыны, В-математика сабағы өтетін аудиториядағы орындықтар жиыны. А және В жиындары арасындағы сәйкестік„ а студент в орындыққа отырады" берілген, мұндағы аеА, веВ.
а) Осы сәйкестік бейнелеу бала ма?
б) Осы сәйкестік А жиынын В жиынына бейнелеу болуының шарттарын тұжырымдаңыздар
6. 2. А={0, 5-7, 13} жене В={х, у, 2} жиындарының арасында графиктері мынадай жиындар болатын әр түрлі сәйкестіктер анықталған.
а) {(0, х), (5 ) Х ), (-7, у), (13, 2) }
б) {(0, у), (-7, х), (-7, у), (13, z), (5, х) }
в) {(0, z), (0, х), (0, у), (5, z) (-7, y) (13, z) }
Осы сәйкестіктердің қайсысы бейнелу болады.
6. 3. Х={хХz, -1<х<3} және У=Z екі жиын берілген. Олардың арасындағы сәйкестік ф={(-1, 3), (0, 2), (1, 5), (2, 2), (3, 0) } графигі арқылы берілген.
а) Осы сәйкестік бейнелеу бола ма?
б) Берілген сәйкестіктің және оған кері сәйкестіктің графигін салыңыздар.
6. 4. А={3, 6, 9} және В={m, n} жиындары берілген.
а) АхВ және ВхА жиындарының барлық элементтерін жазыңыздар.
б) АхВ және ВхА жиындарының арасында өзара бірмәңді сәйкестік құрыңыздар.
6. 5. Х={0, 1, 2, 3, 4, 5 } жиынында Р қатысы у=2х тендеуімен берілген. X жиыны өз-өзіне бейнелеу бола ма?
6. 6. X және у жиындарының арасындағы бейнелеу графигіне тиісті парлар {(а, 2), (в, 2), (с, 4), (d, 5), (е, 4) } берілген.
а) Берілген бейнелеудің анықталу олысы мен мәндерінің жиынын табыңыздар.
б) Бейнелеудің графын құрыңыздар.
6. 7. N-барлық натурал саңдар жиыны. У-барлық натурал сандар квадраттарының жиыны. N жиынын У жиынына өзара бірмәнді бейнелеудің бар болатындығын керсетіңіздер.
6. 8. М-жазықтықтағы геометриялық фигуралар жиыны. R-барлық нақты сандар жиыны. Әрбір фигураға оның ауданының мәніне тең санды сәйкес қоямыз. Осы сәйкестілік М жиынын К жиынына өзара бірмәнді бейнелеу бола ма?
6. 9. Барлық бүтін сандар жиыны z-тен оның өзіне тең қуатты болатын жиын бөліп шығыңыздар.
6. 10. А-жұп натурал сандар.
В -1/n, nеN түріндегі бөлшектер.
С-2 n , nеN түріндегі сандар.
Д-1/2n, nеN түріндегі бөлшектер жиыны берілген.
Тең қуатты жиын парларын атаңыздар. Берілген жиындардың қайсысы N жиынына тең қуатты.
Тақырып 7. Алгебралық операция туралы түсінік
7. 1. Z бүтін сандар жиынында қайсы алгебралық операция?
а) қосу б) көбейту в) (х, у) -»х 2 -у 2 (операция формуламен берілген), коммукативті.
7. 2. (*, В) пары "*В жиынындағы алгебралық операция" қандай түбірлер үшін шын:
а) *-қосу, В-натурал сандар жиыны. б) *-қосу, В-Зк түріңдегі бүтін сандар жиыны.
7. 3. N-натурал сандар жиынында:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz