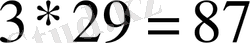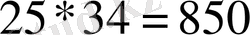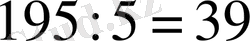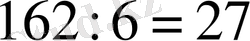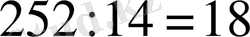Ежелгі Мысыр математикасының тәсілдері: көбейту, бөлу және ондықтан екілікке түрлендіру


Жұмыс түрі: Іс-тәжірибеден есеп беру
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:
Қазақстан Республикасының Білім және ғылым министрлігі
Бағыты: Экономикалық және әлеуметтік үрдістерді математикалық моделдеу
Секция: Математика
Тақырыбы: Ежелгі Мысыр математикасының тәсілдері
АҢДАТПА
Жұмыста бұдан 4 мың жылдай бұрынғы біріккен қуатты мемлекет болған ежелгі Мысыр елінің математикасының тәсілдері қарастырылады. Алдымен ежелгі Мысырдағы арифметика тарихы беріліп, Ежелгі Мысыр тәсілімен есеп шығарудың ережелері (натурал сандарды көбейту және бөлу тәсілдері) келтіріледі. Мысыр тәсілі арқылы ондық жүйеде берілген бүтін санды екілік санау жүйесінде өрнектеу ережесі беріледі.
МАЗМҰНЫ
1
2
2. 1
2. 2
3
3. 1
3. 2
Ежелгі Мысыр математикасының тарихи дамуы
Ежелгі Мысыр тәсілімен есеп шығарудың ережелері
Ежелгі Мысыр тәсілімен сандарды көбейту ережесі
Ежелгі Мысыр тәсілімен сандарды бөлу ережесі
Ертедегі мысырлықтардың қолданған есептеу жүйелері
Мысырдағы ондық санау жүйесі
Мысырдағы екілік санау жүйесі
4
7
7
9
10
10
11
Қорытынды
Пайдаланылған әдебиеттер тізімі
13
14
КІРІСПЕ
Біздің заманымыздан 2000 жыл бұрын жазу-сызу мәдениеті гүлденген, тарихқа әйгілі Мысыр елінің айтулы абыздары қосу, азайту және көбейту есептерін алғаш рет шешкен және оны кең тұтынған.
Ежелгі Мысыр оқымыстылары өздерінің ғылыми еңбектерін папирустарға жазып қалдырған. Мысырлық математика папирустарында бөлшектерді «бірліктерге» жіктеу кестелері, кейбір геометриялық фигураларды аудандарын және көлемдерін есептеп шығару ережелері, ескерткіштердің салмағын анықтауға берілген есептер, статуялар орнату үшін қажетті құрылыс материалдары мен күн санын табуға берілген және басқа да практикалық есептер бар.
Натурал сандарды арифметикалық қосу және азайту амалдары мысырлықтарда негізінен қазіргі кездегідей орындалатын, ал көбейту және бөлуді мысырлықтар тізбектеп екі еселеу мен қосуға келтіретін.
Ежелгі Мысыр тәсілімен есеп шығарудың ережелерін қазақтан шыққан тұңғыш физика-математика ғылымдарының докторы, ұлағатты ұстаз, профессор-математик, қазақтың Ұлттық Академиясының академигі, Қазақстан ғылымына еңбегі сіңген қайраткер Орынбек Ахметбекұлы Жәутіков өзінің 1969 жылы жарық көрген математика тарихы жайындағы еңбегінде көрсеткен.
Зерттеу жұмысының өзектілігі:
Ежелгі Мысыр тәсілімен есеп шығарудың ережелерін 18 ғасырға дейін көп математиктер ерекше арифметикалық амалдар ретінде қарастырып келді. Қазір олар арифметикалық амалдардың дербес жағдайлары болып саналады. Оқушылардың мұндай амалдарды игеруі, олардың математикалық ойлау қабілеттерін дамытады.
Зерттеудің мақсаты мен міндеттері:
Ежелгі Мысыр тәсілімен есеп шығарудың ережелері арқылы оқушыларды математикаға, яғни есептеуге қызықтыру.
Зерттеудің әдісі:
Талдау, сұхбаттасу, бақылау.
Зерттеудің жаңашылдығы мен практикалық маңыздылығы:
Ежелгі Мысыр тәсілімен бүтін сандарды көбейту және бөлудің ережелері игерілді, ондық санау жүйесінде берілген сандарды екілік санау жүйесінде өрнектеу тәсілі берілді. Арифметикалық амалдарды оқушылар есеп шығаруда қолдана алады.
1 Ежелгі мысырдағы математиканың дамуы
Ежелгі Мысыр бұдан 4 мың жылдай бұрын біріккен қуатты мемлекет болып тұрды. Осы кезде құрылыс аса күшті қарқынмен жүріп, архитектура аса өркендеп биік дәрежеге көтеріледі, жер өлшеу, теңізде жүзіп, жан-жақпен кеңінен экономикалық-саяси байланыс жасау қажеттігі күшейеді. Мысыр пирамидалары мұның айғағы болып табылады (1, 2-суреттер) .

Сурет 1 - Ежелгі мысырдағы пирамидалар - перғауындардың мазарлары

Сурет 2 - Ең үлкен Хеопс пирамидасы (б. э. дейінгі ІІІғ. ), биіктігі 146м.
Орасан зор пирамидалар мен ғимараттарды салу үшін, фигуралардың ұзындығын, ауданын, көлемін есептей алу үшін, әрине, арифметиканы білу қажет болды. Арифметика сандармен және санды (арифметикалық) өрнектермен айналысуды үйретеді.
Ежелгі Мысырда бұдан 4 мың жылдай бұрын сандарды белгілеу үшін олар басқа таңбалар мен иероглифтерді қолданған. Бірлік қазықпен, ондық қос қол тәрізденіп белгіленген, жүздік бүктелген пальма жапырағымен, мың молшылық символы ретіндегі лотос гүлімен, жүз мың бақамен белгіленген, өйткені Ніл өзені тасығанда бақалар тіпті көбейіп кететін (3, 4-суреттер) .
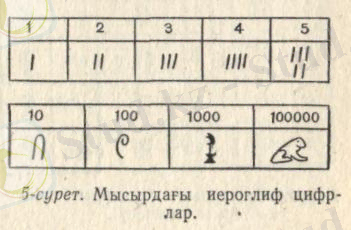
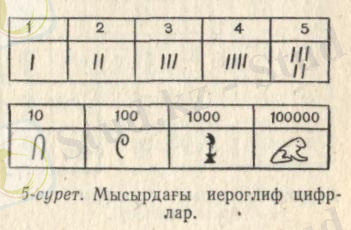
Сурет 3 - Мысырдағы иероглиф цифрлары

Сурет 4 - Мысырдың иероглифтік нумерациясы. 35736 саны.
Ежелгі Мысыр оқымыстылары өздерінің ғылыми еңбектерін папирустарға жазып қалдырған. Папирус дегеніміз ежелгі Мысыр жерінде көп өсетін папирус деп аталатын тропиктік ірі өсімдіктердің сабағынан жасалған аса берік те төзімді орамдар беті, яғни жазу материалы.
Біздің заманымызға дейін сақталып келген ең көне математикалық папирус - Москвалық папирус деп аталады - Москвада А. С Пушкин атындағы музейде сақтаулы, б. э. дейінгі 1850 жылы жазылған папирус. Оның ұзындығы 5, 5 м, ал ені 8 см, онда 25 есеп келтірілген.
Мазмұны жағынан аса маңызды папирус - Ахмес папирусы (5-сурет), Ежелгі Мысырдағы мұны жазған хатшының есімімен аталған папирус - Лондонда Британ музейінде сақтаулы. Оның ұзындығы 5, 5 м, ал ені 33 см. Бұл папирусты Ринд деген ағылшын иемденген болатын, сондықтан оны кейде Ринд папирусы деп те атайды, мұнда 85 есеп келтірілген.

Сурет 5 - Ахмес папирусының үзіндісі
Ғалымдар сақталған папирустардағы жазуларды анықтап танығаннан кейін, бұдан 4 мың жыл бұрынғы кездің өзінде мысырлықтар ондық (бірақ позициялық емес) санау жүйесін қолданған, сондай-ақ құрылыс, сауда және әскери істермен байланысты көптеген есептерді шығара білген.
Папирустарда келтірілген есептер қысқа түрде берілген, яғни есептің шарты мен талабы беріледі де шешу жолы көрсетіледі. Ешқандай дәлелдеу, тексеру жоқ, барлығы иероглиф арқылы өрнектелген сөздер мен сөйлемдерден тұрады.
4 мың жылдай бұрынғы мысырлықтар жер өлшеу, құрылыс және әскери істерінің әр түрлі есептерін теңдеулер құрып шығарған. Мысырлықтар белгісізді «Үймек» - «Аха» деп атаған.
Ахмес папирусындағы бір есеп және оны шешу мысалы мынадай:
Есеп 1. Үймек және онымен 7-ні бірге алғанда 15 болады.
Бұл есепті қазіргіше шығарғанда

теңдеуі құрылады.
Мұны шешкенде табатынымыз:
 .
.
Москвалық папирусындағы бір есеп.
Есеп 2. Аулада 7 үй бар. Әр үйде 7 мысық бар. Әр мысық 7 тышқан жейді. Әр тышқан 7 дән жейді. Дәндердің санын табу керек.
Бұл есептің шешуі:
 .
.
Мысырлық математика папирустарында бөлшектерді «бірліктерге» жіктеу кестелері, кейбір геометриялық фигураларды аудандарын және көлемдерін есептеп шығару ережелері, ескерткіштердің салмағын анықтауға берілген есептер, статуялар орнату үшін қажетті құрылыс материалдары мен күн санын табуға берілген және басқа да практикалық есептер бар.
2 Ежелгі Мысыр тәсілімен есеп шығарудың ережелері
2. 1 Ежелгі Мысыр тәсілімен сандарды көбейту ережесі
Біздің заманымыздан 2000 жыл бұрын жазу-сызу мәдениеті гүлденген, тарихқа әйгілі Мысыр елінің айтулы абыздары қосу, азайту және көбейту есептерін алғаш рет шешкен және оны кең тұтынған.
Натурал сандарды арифметикалық қосу және азайту амалдары мысырлықтарда негізінен қазіргі кездегідей орындалатын, ал көбейту және бөлуді мысырлықтар тізбектеп екі еселеу мен қосуға келтіретін.
Ежелгі Мысыр тәсілімен есеп шығарудың ережелерін қазақтан шыққан тұңғыш физика-математика ғылымдарының докторы, ұлағатты ұстаз, профессор-математик, қазақтың Ұлттық Академиясының академигі, Қазақстан ғылымына еңбегі сіңген қайраткер Орынбек Ахметбекұлы Жәутіков өзінің 1969 жылы жарық көрген математика тарихы жайындағы еңбегінде көрсеткен.
Ежелгі Мысыр тәсілімен сандарды көбейту ережесін қарастырайық:
- Екі қатар бағаннан тұратын кесте құрамыз;
- Сол жақ бағанға 1-ден бастап екі еселенген сандарды, оң жақ бағанға екінші көбейткіштен бастап екі еселенген сандарды жазамыз;
- Әрбір келесі сан алдындағы санның екі есесіне (өзіне-өзі қосқанға) тең;
- Сол жақ бағандағы соңғы сан бірінші көбейткіштен артпауы тиіс;
- Сол жақ бағандағы сандардың ішінен қосындысы бірінші көбейткішке тең болатын сандарды төменнен жоғары қарай сайлап алып, солардың тұстарына көлбеу сызықтар қою керек;
- Көлбеу сызықтар жүргізілген сандарға қарсы тұрған екінші қатардағы сандарды қосу керек.
Мысал 1. 3 -ті 29 -ға мысырлықтарша көбейту үшін екі қатар бағаннан тұратын мынадай кесте құру керек:
Мысал 2. 5 -ті 115 -ке мысырлықтарша көбейтейік:

Мысал 3. 7 -ні 79 -ға мысырлықтарша көбейтейік:
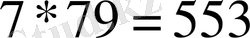
Мысал 4. 13 -ті 15 -ке мысырлықтарша көбейтейік:
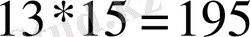
Мысал 5. 12 -ні 18 -ге мысырлықтарша көбейтейік:
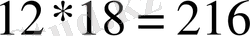
Мысал 6.
Көбейтуді орында:
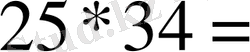
Осы әдісті көбейткіштердің бірі тұрақты болып келетін кейбір жағдайда қолдану ұтымды болады.
Мысалы, мынадай есепті шығару керек болсын:
Алыс сапарға баратын поезд орта есеппен 57 км/сағ жылдамдықпен жүреді. Ол 8 сағатта қандай ара қашықтықты жүріп өтеді? 12; 15 сағатта ше?
Келесі кестені құрайық:
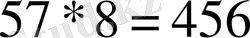 км;
км;
 км;
км;
 км.
км.
2. 2 Ежелгі Мысыр тәсілімен сандарды бөлу ережесі
Ежелгі Мысыр тәсілімен сандарды бөлу амалы көбейтуге кері бағытта келтіріледі:
- Екі қатар бағаннан тұратын кесте құрамыз;
- Сол жақ бағанға 1-ден бастап екі еселенген сандарды, оң жақ бағанға бөлгіштен бастап екі еселенген сандарды жазамыз;
- Әрбір келесі сан алдындағы санның екі есесіне (өзіне-өзі қосқанға) тең;
- Оң жақ бағандағы соңғы сан бөлінгіштен артпауы тиіс;
- Оң жақ бағандағы сандардың ішінен қосындысы бөлінгішке тең болатын сандарды төменнен жоғары қарай сайлап алып, солардың тұстарына көлбеу сызықтар қою керек;
- Көлбеу сызықтар жүргізілген сандарға қарсы тұрған сол жақ қатардағы сандарды қосу керек.
Мысал 7.
Бөлуді орында:

Мысал 8.
Бөлуді орында:

Мысал 9.
Бөлуді орында:
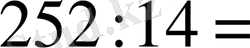
3 Ертедегі мысырлықтардың қолданған есептеу жүйелері
3. 1 Мысырдағы ондық санау жүйесі
Ертедегі мысырлықтардың қолданған есептеу жүйесі иероглифтік ондық жүйе болған.
Он-оннан топтап санауды
ондық санау жүйесі
немесе ондық нумерация
деп атайды, яғни біз он-оннан санайтынымыз белгілі: он бірліктен бір ондық, он ондықтан бір жүздік т. с. с. құралады, басқаша айтқанда: бірінші разрядтың он бірлігінен екінші разрядтың бір бірлігі, екінші разрядтың он бірлігінен үшінші разрядтың бір бірлігі т. с. с. құралады. Он саны ондық санау жүйесінің
негізі
деп аталады. Олар мына
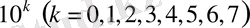 түрдегі түйіндік сандарды таңбалау үшін арнаулы иероглифтік таңба (6-сурет) .
түрдегі түйіндік сандарды таңбалау үшін арнаулы иероглифтік таңба (6-сурет) .
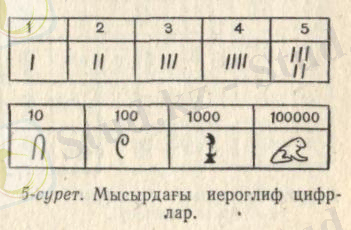
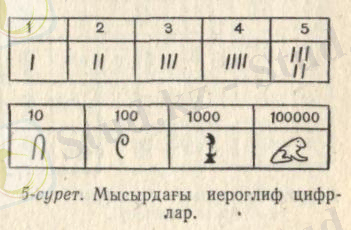
Сурет 6 - Мысырдағы ондық санау жүйесі
3. 2 Мысырдағы екілік санау жүйесі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz