Ньютон ашқан заңдылық

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

Жоспар

I Кіріспе

II Негізгі бөлім

Ньютон ашқан заңдылық
Бүкіл әлемдік тартылыс заңы
Кеплер заңдары

III Қорытынды

IV Пайдаланылған әдебиеттер

Кіріспе

Ньютон тартылу күшінің өрнегін 1666 ж., 24 жасында-ақ анықтаған. Бірақ, ол өзінің теориясын тәжірибелік деректермен салыстырып, көп алшақтық байқағандықтан жария етпейді. Нәтижесінде ол ашқан заң көптеген жылдар бойы белгісіз болып қалды. Алайда, ол қолданған деректер нақты дәл емес. Ньютонға дәлірек өлшеулердің нғтижелері белгілі болғанда, О. Лодж айтқандай, ол “өзінің ескі қолжазбаларын алып есептеуге кірісті… Жаңа деректер есептеу нғтижелерін өзгерте бастады. Ол өз жұмысын керемет тебіреніспен қайта қарады. Қаламы ойына ілесе алмады. Соңында есептеулерден керекті нғтиже алды. Ашқан заңның керемет мәні мен тереңдігі оның басын айналдырып, тұманданған көздері қолжазбаны көрмеді. Шаршаған ол қаламын тастай салады. Әлем құрылымының құпиясы жалғыз өзіне ғана ашылды.

1. 1 Ньютон ашқан заңдылық

Бүкіл әлемдік тартылыс заңы , Ньютонның тартылыс заңы - кез келген материялық бөлшектер арасындағы тартылыс күшінің шамасын анықтайтын заң. Ол И. Ньютонның 1666 ж. шыққан “Натурал философияның математикалық негіздері” деген еңбегінде баяндалған. Бұл заң былай тұжырымдалады: кез келген материялық екі бөлшек бір-біріне өздерінің массаларының (m1, m2) көбейтіндісіне тура пропорционал, ал ара қашықтығының квадратына (r2) кері пропорционал күшпен (F) тартылады:, мұндағы G - гравитациялық тұрақты. Гравитациялық тұрақтының (G) сан мәнін 1798 ж. ағылшын ғалымы Г. Кавендиш анықтаған. Қазіргі дерек бойынша G=6, 6745(8) Һ Һ10-8см3/гҺс2=6, 6745(8) Һ

Һ10-11м3/кгҺс2. Айдың Жерді, планеталардың Күнді айнала қозғалуын зерттеу нәтижесінде И. Ньютон ашқан бұл заң табиғаттағы барлық денелерге және олардың барлық бөліктеріне қолданылады. Б. ә. т. з. аспан денелерінің қозғалысы жайындағы ғылым - аспан механикасының іргетасын қалайды. Осы заңның көмегімен аспан денелерінің қозғалу траекториясы есептелінеді және олардың аспан күмбезіндегі орындары алдын ала анықталады. Уран планетасының осы заңға сәйкес есептелінген орбитадан ауытқуы бойынша 1846 ж. Нептун планетасы ашылды. Плутон планетасы да 1930 ж. осындай тәсілмен анықталды. 19 - 20 ғ-ларда бұл заңды алдымен қос жұлдыздарға, сонан соң шалғай орналасқан галактикаларға да пайдалануға болатындығы белгілі болды. Жалпы салыстырмалық теориясының ашылуы (1916) нәтижесінде тартылыс күшінің табиғаты онан әрі айқындала түсті. Шындығында кез келген дене кеңістікте тартылыс өрісін туғызады. Денелердің арасындағы тартылыс күші осы өріс арқылы беріледі. Өте майда бөлшектерден тұратын микродүниедегі (атом, атом ядросы, элементар бөлшектер, т. б. ) құбылыстарда Б. ә. т. з-ның әсері сезілмейді. Өйткені онда күшті, әлсіз және электр магниттік өзара әсерлер (қ. Әлсіз өзара әсер, Күшті өзара әсер, Электр магниттік өзара әсер) тәрізді өрістік әсерлер басым болып келеді.

Бүкіл әлемдік тартылыс заңы

Табиғаттағы барлық денелер бір-біріне тартылады. Осы тартылыс бағынатын заңды Ньютон анықтап, бүкіл әлемдік тартылыс заңы деп аталған. Осы заң бойынша, екі дененің бір-біріне тартылатын күші осы денелердің массаларына тура пропорционал, ал олардың ара қашықтығының квадратына кері пропорционал болады:

мұндағы, G - гравитациялық тұрақты деп аталатын пропорционалдық коэффициент. Бұл күш бір-біріне әсер ететін денелер арқылы өтетін түзудің бойымен бағытталған. Формула шамасы бойынша бір-біріне тең F ₁₂ және F ₂₁ күштердің сандық мәнін береді. Cуреттегі өзара әсерлесетін денелер біртекті шарлар болса, m ₁ және m ₂ - шар массалары, r - олардың центрінің ара қашықтығы. Сонымен, шарлар материялық нүктелер ретінде өзара әсерлеседі, ал олардың массалары шар массаларына тең және олардың центрлерінде орналасқан. Гравитациялық тұрақтының сандық мәні, массалары белгілі денелердің бір-біріне тартылатын күшін өлшеу жолымен анықталған. Осындай өлшеу кезінде көп қиыншылықтар кездеседі, өйткені массалары тікелей өлшенетін денелер үшін тартылыс күштері өте-мөте аз болып шығады. Мысалы, әрқайсысының массасы 100 кг, бір-бірінен қашықтығы 1 метр болатын екі дене бір-біріне шамамен 10 ^-6 Н, яғни 10 ^-4 Г күшпен өзара әсер етеді.

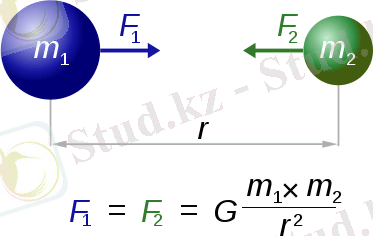Ньютонның бүкіләлемдік тартылыс заңының іске асуы; m ₁ нүктелік массасы басқа бір m ₂ нүктелік массасын F ₂ күшімен тартады; бұл күш екі массаның көбейтіндісіне тура, ал олардың арасындағы қашықтыққа ( r ) кері пропорционалды. Масса немесе қашықтыққа қарамастан F ₁ және F ₂ әрқашан тең болады. Мұндағы G - гравитациялық тұрақты. ХVІІ ғ. ортасында ғалымдарды денелердің өзара тартылу күшінің ара қашықтыққа тғуелділігі ойлантты. Мысалы Күн планеталарды қандай күшпен тартады? Р. Гук 1674 ж. осы мәселе жайында былай деді: “Әсер ету орталығына денелер неғұрлым жақын орналасса тарту күштері соғұрлым көбірек болады. Бұл күштің ара қашықтыққа қандай тғуелділікте екендігін мен ғлі тәжірибеде анықтағаным жоқ”. Гуктің замандастары тарту күшінің өрнегін тауып, оның негізінде планеталар траекториясын анықтай алмады. Бұл мәселе жөнінде Гуктің ойы болды, бірақ оларды дәлелдей алмады. 1683 ж. Гук осы мәселемен айналысып жүрген ғалымдар К. Рен және Э. Галлеймен тартылыс туралы ой бөлісу үшін арнайы кездесті. Бірақ бұл үш ғалымның кездесуі нғтижесіз болды. Тұйыққа тірелген Галлей осы мәселемен Ньютонға келді. Бұл мәселенің шешімі Ньютонға көптен белгілі екенін естіген ол қатты таңқалып қуанады!Ньютон тартылу күшінің өрнегін 1666 ж., 24 жасында-ақ анықтаған. Бірақ, ол өзінің теориясын тәжірибелік деректермен салыстырып, көп алшақтық байқағандықтан жария етпейді. Нәтижесінде ол ашқан заң көптеген жылдар бойы белгісіз болып қалды. Алайда, ол қолданған деректер нақты дәл емес. Ньютонға дәлірек өлшеулердің нғтижелері белгілі болғанда, О. Лодж айтқандай, ол “өзінің ескі қолжазбаларын алып есептеуге кірісті… Жаңа деректер есептеу нғтижелерін өзгерте бастады. Ол өз жұмысын керемет тебіреніспен қайта қарады. Қаламы ойына ілесе алмады. Соңында есептеулерден керекті нғтиже алды. Ашқан заңның керемет мәні мен тереңдігі оның басын айналдырып, тұманданған көздері қолжазбаны көрмеді. Шаршаған ол қаламын тастай салады. Әлем құрылымының құпиясы жалғыз өзіне ғана ашылды…”. Ньютон алғашында еркін құлау үдеуінің ара қашықтыққа тғуелділігін анықтады. Ол Жер бетінде, демек оның ортасынан 6400 км қашықтықта еркін түсу үдеуі 9, 8 м/с ² , ал 60 есе үлкен қашықтықтағы Айда: 3600 = 60 ² . Демек, еркін түсу үдеуі Жер ортасынан ара қашықтықтың квадратына кері пропорционал азаяды. Ньютонның екінші заңына сәйкес үдеу күшке пропорционал. ‡деудің осылай азаюы тартылу күшінің ара қашықтықтан тура сондай тғуелділігінен. Тарту күшінің толық формуласын, бұл күштің әсерлесуші денелердің гравитациялық зарядтарына, демек олардың m ₁ және m ₂ массаларына пропорционал екендігін ескергенде анықтауға болады. Сонымен,

F =: F =

G: G

m1m2: m ₁ m ₂

.: .

(40. 1): (40. 1)

: r ²

Ньютон Жердің оған тартылатын денелермен анықтайтын өрнекті тапты. Өз интуициясына сенген ол анықталған формуламен өзара ара қашықтығымен r салыстырғанда өлшемі аз болатын Әлемдегі кез-келген денелер арасындағы тартылу күшін есептеуге болады деп ойлады. Сондықтан ол өзі анықтаған өрнекті аспан денелеріне де, Жер бетіндегі денелер үшін де дұрыс болатын бүкіләлемдік тартылыс заңы ретінде қарастырды. Ғылымның әрі қарай дамуы Ньютон заңының дұрыстығын, бұл заңды атомдар мен молекулалардан бастап керемет үлкен жұлдыздар шоғына да қолдануға болатындығын көрсетті.

Сонымен, Ньютон ашқан бүкіләлемдік тартылыс заңы былай тұжырымдалады:

Кез-келген екі бөлшектің гравитациялық тартылу күші олардың массаларының көбейтіндісіне тура пропорционал, ал олардың ара қашықтығының квадратына кері пропорционал.

Бұл заң математикалық түрде (40. 1) формуламен өрнектеледі. Бұл формуладағы G - пропорционалдық коэфициенті гравитациялық тұрақты деп аталады.

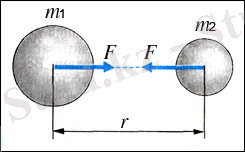
Бұл жерде бүкіләлемдік тартылыс заңы бөлшектер үшін, демек, өлшемдері r ара қашықтығынан ғлдеқайда аз денелер үшін тұжырымдалған. Алайда бұл заңның керемет бір ерекшілігі оны басқа да жағдайларда қолдануға мүмкіндік береді. Тартылу күшінің бөлшектерден ара қашықтығының үшінші немесе төртінші дәрежесіне емес, тек квадратына тғуелділігі бұл заңның аталған ерекшілігі. Есептеулер көрсеткеніндей тура осыған байланысты (40. 1) - формуланы ішіндегі заты сфералық- симметриялы таралған шар тәрізді дғнелердің арасындағы ара қашықтықтың кез-келген мәні үшін қолдануға болады. Бұл жағдайды r -денелер арасындағы қашықтық емес, сол денелердің орталықтары арасындағы қашықтық (35-сурет) . (40. 1) формула аралық жағдайда да дұрыс, мысалы өлшемі кез- келген сфералық дене материаялық нүктемен әсерлескенде. Осы жағдай бүкіләлемдік тартылу формуласын Жер шарының заттарды тарту күшін есептеуге мүмкіндік береді.

: 35-сурет

Аңыз бойынша Ньютонға бүкіләлемдік тартылыс туралы ой, ол өз бағында демалып отырғанда құлаған алма себеп болған. Ньютонның аяғына дәл уақытында құлаған алманың ағашы елеусіз қалмай, оның бөлшектері Англияда осы уақытқа дейін сақталып келеді деген сөз бар.

1. 3 Кеплер заңдары

Кеплер заңдары - 17 ғ-дың басында И. Кеплер ашқан планеталар қозғалысының үш заңы. Кеплердің “Жаңа астрономия”(1609) атты негізгі еңбегінде алғашқы екі заң баяндалған. Үшінші заң кейінірек ашылған және ол “Әлем гармониясы” (1619) атты 5-кітабының 3-тарауында берілген.

Кеплердің бірінші заңы.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.