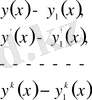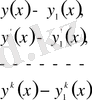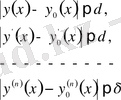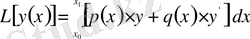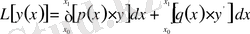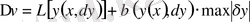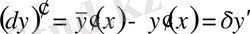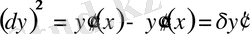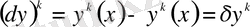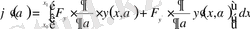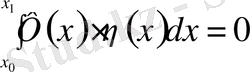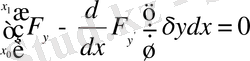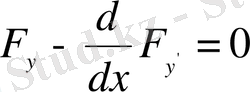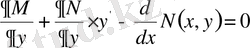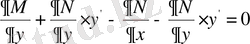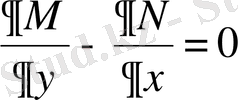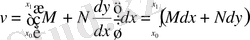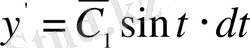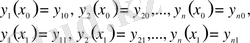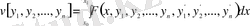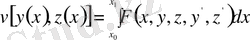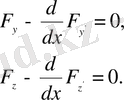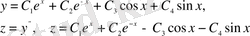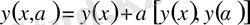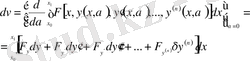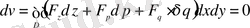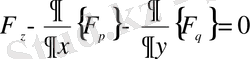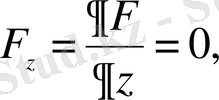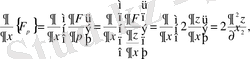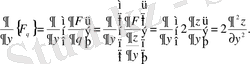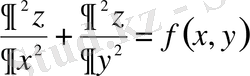Вариациялық есептеулер пәні

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 54 бет
Таңдаулыға:

вариациялық есептеулер пәні.

№ 1 Лекция

Кіріспе.

Белгілі бір 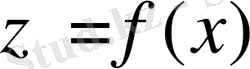функциясының экстремал мәндерін (min, max) анықтауды қажет ететін есептермен қатар, жаратылыстану ғылымдарында функционал деп аталатын ерекше бір шамалардың экстремал мәндерін анықтау қажеттілігі туады. Функционал деп, мәндері бір немесе бірнеше функцияларды таңдау арқылы анықталатын, айнымалы шамаларды айтады.

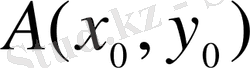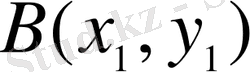Мысалы, жазықтықта берілген және нүктелерінің арасын қосатын кез келген қисықтың ұзындығы функционал болады. Егер қисықтың теңдеуі 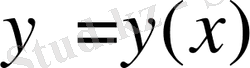түрінде берілген болса, онда ұзындығы былайша анықталады:

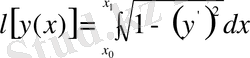Сол сияқты, кеңістіктегі кез келген 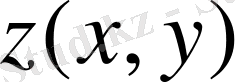беттің ауданы да функционал. Себебі, ауданының шамасы беттің 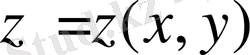теңдеуіндегі функциясының түріне тәуелді:

Бұл жерде, - қарастырылып отырған бетінің жазықтығына проекциясы.

Функционалға мысал ретінде, механика ғылымында қолданылатын инерция моменттері, статикалық моменттер, кеңістіктегі қисықтың немесе беттің ауырлық орталығының координаталары сияқты шамаларды айтуға болады.

Варияциялық есептеулер ғылымы

Вариациялық есептеулер ғылымы функционалдардың экстремумдарын ( min немесе max ) табудың әдістерін зерттейді. Ал функционалдардың min немесе max- ын іздеуді қажет ететін есептер вариациялық есептер деп аталады.

Вариациялық есептер, механика және физика ғылымдарында зерттелетін көптеген процестерде белгілі бір функционалмен сипатталатын шамалардың min немесе max- ға тең болуын талап ететін заңдардан туындайды. Осылайша сипатталған заңдар вариациялық принциптер деп аталады. Вариациялық принциптерге : энергияның сақталу заңы, импульстің сақталу заңы, қозғалыс мөлшерінің моментінің сақталу заңы және т. б жатады. Сонымен қатар, вариациялық принциптерге - оптикада Ферма принципін, серпімділік теориясында Кастилиано принципін және т. б. атауға болады.

Шеткі нүктелері қозғалмайтын есептерге вариация әдісін қолдану.

Вариация және оның қасиеттері.

Анықтама: Егер белгілі бір класынан алынған әрбір 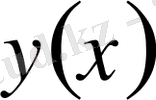функциясына нақты бір мәні сәйкес келетін болса, онда бұл айнымалы шамасы функционал деп аталады да, былайша белгіленеді: .

Бірнеше функцияға тәуелді, немесе, бірнеше айнымалының функциясына тәуелді функционалдар да осылайша анықталады.

Функционалға мысалдар:

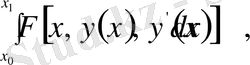
Вариациялық есептеулер теориясында 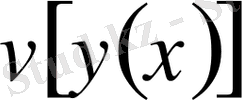функционалының 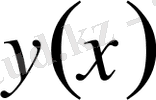аргументінің өсіндісі немесе варияциясы деп екі функцияның 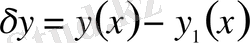айырымын айтады. Бұл жердегі 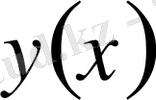функциясы функциялардың белгілі бір класында еркін өзгереді деп есептеледі. Егер 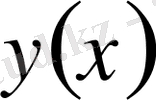функциясының шағын өзгеруіне 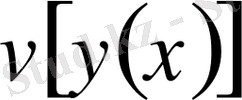функционалының шағын өзгеруі сәйкес келсе, онда бұл функционал үздіксіз функционал деп аталады.

Енді функционалдың 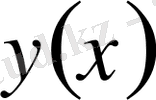және 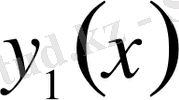аргументтерінің 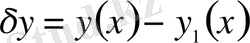айырымы арқылы функциялардың өзара жақындық деңгейін бағалайық.

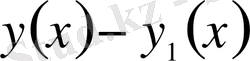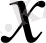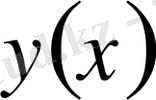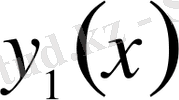Егер айырымының модулі -тың барлық мәндері үшін кіші сан болатын болса, онда бұл функциялардың ординаталары өзара жақын мәнді сандар болады да және функциялары өзара жақын функциялар деп аталады.

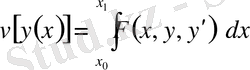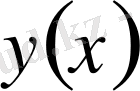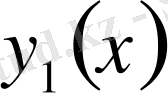Бірақ, кейбір жағдайларда, әсіресе функционалын қарастырған кезде пен функцияларының ординаталары өзара жақын болғанымен, олардың, белгілі бір 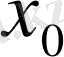нүктесіндегі 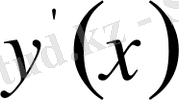және 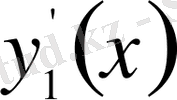жанамаларының айырымы өте үлкен болуы мүмкін.

Сондықтан, екі функцияны өзара жақын деп айту үшін олардың ординаталарының айырымымен қатар олардың жанамаларынының айырымының да кіші болуын талап ету қажет. Демек, жалпы жағдайда, 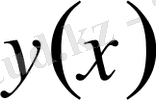пен 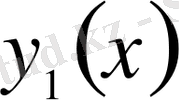қисықтарын өзара жақын деп есептеу үшін

айрымдарының бәрінің де модульдері кіші сандар болуы керек. Осыған байланысты мынадай анықтама енгіземіз.

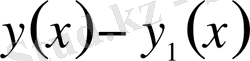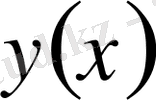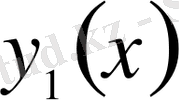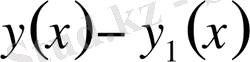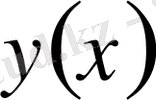Анықтама : Егер айырымының модулі кіші сан болса, онда және қисықтары нолдік реттегі өзара жақын функциялар деп аталады. Ал егер ординаталар айырымы мен жанамалар айырымының модулдері кіші сан болса, онда және 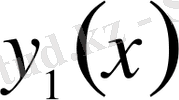функцияларының жақындығы бірінші ретті деп аталады.

Жалпы жағдайда

айырымдарының модулдері кіші сан болса, онда бұл функциялар өзара 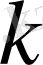ретті жақын функциялар деп аталады.

Келесі суретте өзара нолдік реттегі жақын функциялар көрсетілген. Бірақ оның жақындығы бірінші ретке жетпейді. Себебі жанамалардың айырымы кіші сан емес.

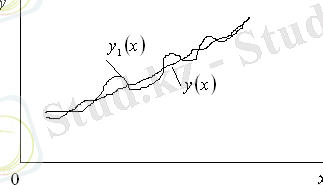
Осы айтылғандарды қорыта келе функционалдың үздіксіздігіне жаңаша анықтама берейік.

Анықтама : Егер 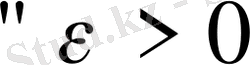саны үшін 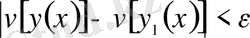теңсіздігі орындалса және осы теңсіздік үшін келесі:

теңсіздіктер орындалатындай санын таңдауға болатын болса, онда 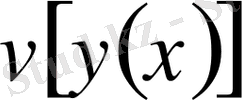функционалы 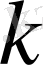ретті үздіксіз функционал деп аталады.

Анықтама: 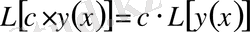шартына бағынатын 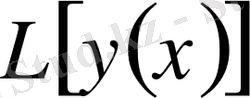функционалы сызықтық функционал деп аталады. Бұл жерде кез келген тұрақты шама, және ол үшін

теңдігі орындалады.

Мысалы:

функционалын қарастырсақ, онда

болуы керек.

Егер функционалдың 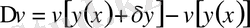өсіндісін

түріне келтіру мүмкін болса, онда бұл өсіндінің сызықтық бөлігі, демек, 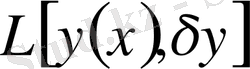шамасы функционалдың вариациясы деп аталып, - арқылы белгіленеді. Бұл жерде, вариация үшін 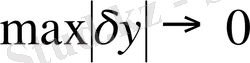болған кезде 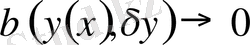шарты орындалады да, 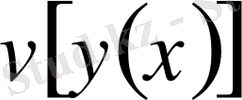функционалының варияциясы нолге теңеседі:

Бұл жерде 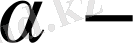параметрі өте кіші сан.

Анықтама : Егер 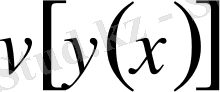функционалының мәні ешқашан 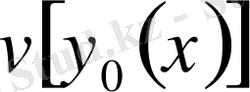функционалының мәнінен артық болмайтын болса, басқаша айтқанда, 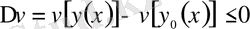болса, онда 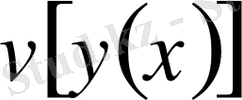функционалы 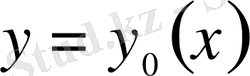қисығында өзінің максимумына жетеді.

Егер 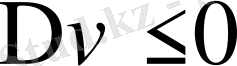болса, және тек 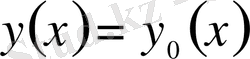болғанда ғана шарты орындалса, онда 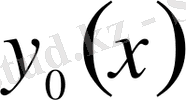қисығында функционал өзінің қатаң максимумына жетеді.

Эйлер теңдеуі

Теорема: Егер 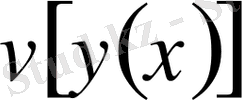функционалы 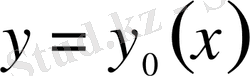қисығында өзінің максимумына немесе минимумына жететін болса, онда оның 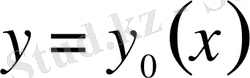қисығындағы варияциясы нолге тең: .

Демек, белгілі бір 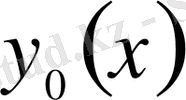және шамалары үшін

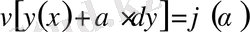
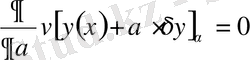өрнегі еркін таңдалған параметрінің функциясы болады да, болғанда функционал өзінің максимумы немесе минимумына (экстремумға) жетеді. Олай болса, функционалдың экстремумға жету шарты , немесе, түрінде жазылады.

Қорыта келгенде, өзінің экстремумын беретін қисықтың бойында функционалдың варияциясы әрқашан нолге тең болады .

Бұл теореманы былайша қолдануға болады: Функционалға экстремум беретін 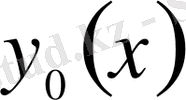қисығын іздеу есебін функционалдың варияциясы 0-ге тең болу шартымен, басқаша айтқанда, теңдеуін шешу есебімен айырбастауға болады.

Енді 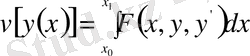функционалын экстремумға зерттейік. Бұл жерде функционалдың анықталу аймағының екі шеткі нүктесі қатаң бекітілген деп қабылданған. Олай болса, функционалға экстремум беретін 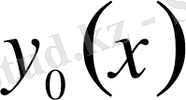қисығы екі шеткі нүктеден басқа жердің бәрінде еркін өзгеруі мүмкін, тек, сол өзгеру жағдайларының ішінде бір ғана жағдай функционалға экстремум береді. Функционалдың бұл түрі бір айнымалыға тәуелді бір функцияның және оның, тәуелсіз айнымалы бойынша, бірінші туындысының функционалы деп аталады. Бұл жерде 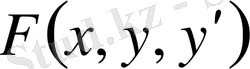функциясының үш рет дифференциялдануы шарт. Енді 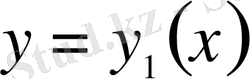қисығында функционал өзінің экстремумына жетеді деп болжайық. Егер қисығына жақын орналасқан 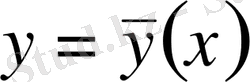қисығын алып, кез келген параметрінің көмегімен 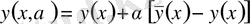өрнегін құрастырсақ, онда параметріне тәуелді қисықтар жиынын аламыз және болған кезде өрнектің мәні болады, ал болған кезде . 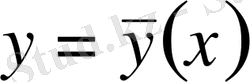Бұл жерде 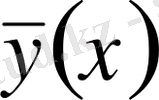салыстыру қисығы деп аталады. Ал айрымы 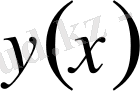функциясының варияциясы деп аталып 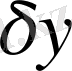арқылы белгіленеді және ол 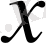-тың функциясы болады. Бұл функция 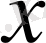бойынша бірнеше рет дифференциялданады және оның туындылары былайша есептеледі:

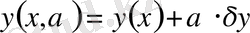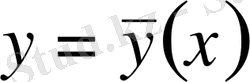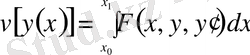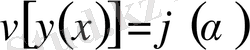Енді, жоғарыда аталған қисықтар жиынын қарастырайық. Егер кезінде болса, ал кезінде болса, онда параметрін енгізу арқылы функционалын параметрінің функциясына айналдырамыз. Осылайша анықталған 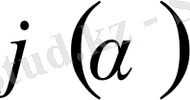функциясы болған кезде өзінің экстремумына жетеді. Демек, оның экстремумының қажетті шарты 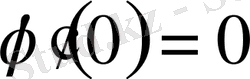түрінде жазылады. Енді, осылайша анықталған 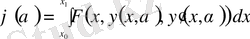функциясының параметрі бойынша туындысын

түрінде анықтайық. Бұл жерде

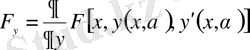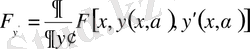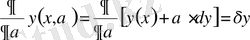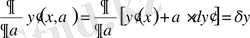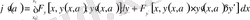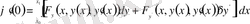Функционалдың экстремумының шарты 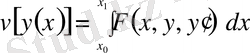функционалы үшін енді былайша жазылады

Интеграл астындағы екінші қосындыны бөлектеп интегралдасақ және 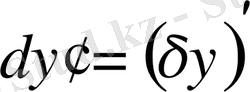екенін ескерсек, онда 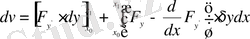. Бірақ

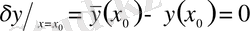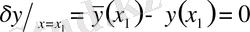, болады. Себебі функционалдың анықталу аймағының екі басы қатаң бекітілген болғандықтан функционалдың ол нүктелердегі варияциялары 0-ге тең: . Олай болса

Бұл функционалдың варияциясын есептеу формуласы. Демек, экстремумның қажетті шарты енді былайша жазылады:

Интеграл астындағы бірінші 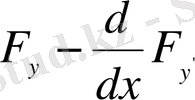көбейткіші берілген үзіліссіз функция, ал екінші көбейткіш кез келген үзіліссіз шама, себебі 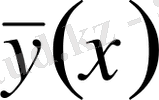салыстыру қисығы еркін таңдалады. Оның үстіне вариациясы функционалдың анықталу аймағының шекаралық және нүктелерінде 0-ге тең. Алынған нәтижені қарапайым түрге келтіру үшін келесі лемманы қолданамыз.

Вариациялық есептеулердің негізгі леммасы:

Егер әрбір үздіксіз 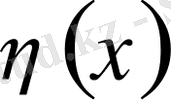функциясы үшін

шарты орындалса, онда, 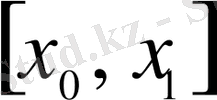аралығында үздіксіз 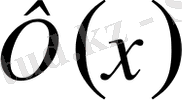функциясы әрқашан

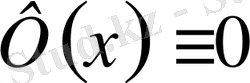
болады.

Енді осы лемманы жоғарыда алынған функционалдың экстремумға жетуінің

шартына қолдансақ, онда, әрқашан

болуы керек екенін көреміз. Шынында, жоғарыда келтіріліген шарттарды 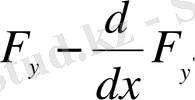көбейткіші қанағаттандырады.

Функционалдың экстремумға жету шартының

түрі Эйлер теңдеуі деп аталып, 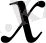бойынша туынды алынғаннан кейін, екінші ретті кәдуілгі диффренциалдық теңдеу түрінде былайша ашылады:

№ 3 лекция.

Қарапайым 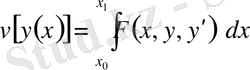функционалдардың

жекелеген түрлері.

Енді, 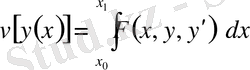функционалына сәйкес алынған 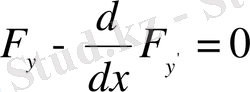Эйлер теңдеуінің 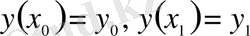шекаралық шарттарды қанағаттандыратын шешімі барлық кезде табыла бермейтінін, ал, табылған кездің өзінде, шешімнің жалғыз болмауы мүмкін екенін ескерейік. Ол үшін функционалдың интеграл астындағы 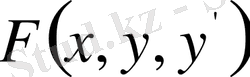функциясының түріне байланысты аталған шекаралық есептің шешімі әр түрлі болатынына мысалдар келтірейік.

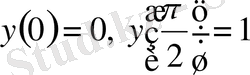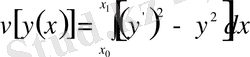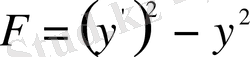
Мысал: Шекаралық шарттары түрінде берілген функционалының экстремалын іздейік. Бұл жерде интеграл астындағы функция түрінде берілген. Енді Эйлер теңдеуінің құрамындағы шамаларды есептейік:

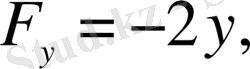
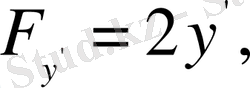
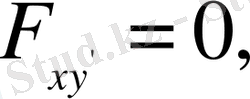
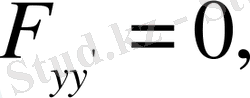
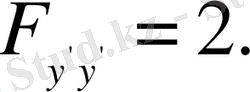
Алынған шамаларды Эйлер теңдеуінің ашылып жазылған 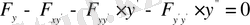формуласына қойсақ, онда 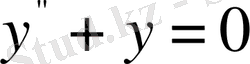түріндегі екінші ретті, кәдуілгі сызықтық дифференциалдық теңдеу аламыз. Бұл теңдеудің жалпы шешімі 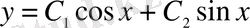болады. Шекаралық шарттардан 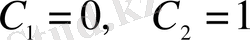екенін анықтаймыз. Олай болса, берілген функционал тек 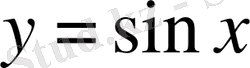қисығында ғана өзінің экстремумына жетеді.

1) жағдайы.

Енді функционалдың 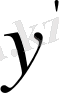туындысына тәуелсіз болатын кезін қарастырайық. Бұл кезде интегралдың астындағы функция 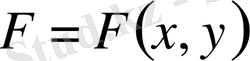түрінде жазылады да, сәйкес Эйлер теңдеуі 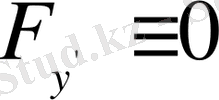болғандықтан 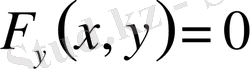түрінде алынады. Бұл теңдеу дифференциалдық теңдеу болмағандықтан, оның құрамында интегралдау кезінде пайда болатын белгісіз коэффициенттері болмайды. Сол себептен мұндай вариациялық есептің жалпы жағдайда шешімі болмайды. Тек 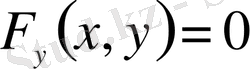қисығы шекаралық нүктелері арқылы өткен кезде ғана функционалға экстремум беретін қисық табылуы мүмкін.

Мысал: 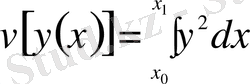; 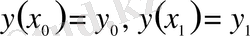вариациялық есебінің Эйлер теңдеуі немесе 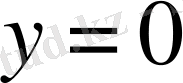түрінде жазылады. Бұл қисық 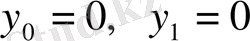болған кезде ғана шекаралық 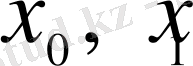нүктелері арқылы өтеді. Қалған 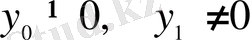жағдайлардың бәрінде де экстремалдық қисықтың теңдеуін үзіліссіз функциялар класынан табу мүмкін емес.

2) функциясы -қа сызықты түрде тәуелді.

Бұл жағдайды жалпы түрде былайша жазамыз: 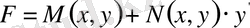. Демек, енді функционал былайша

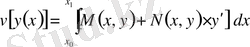
жазылады да, Эйлер теңдеуі

түрінде, немесе

түрінде алынады. Тағы да, алдыңғы жағдай сияқты, Эйлер теңдеуі дифференциалдық түрде емес, шекті түрде алынды. Демек, шекаралық шарттар арқылы анықталатын белгісіз коэффиенттері болмағандықтан 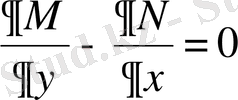қисығы жалпы жағдайда шекаралық шарттарды қанағаттандырмайды да, вариациялық есептің үзіліссіз функциялар класында шешімі болмайды. Ал егер 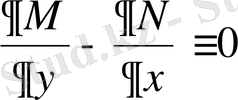болса, онда 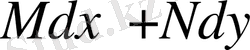өрнегі толық дифференциал болады да

функционалының мәні интегралдау жолына тәуелсіз болып қалып, вариациялық есеп мағынасын жоғалтады.

Мысал:

Вариациялық есеп

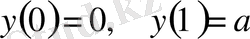
түрінде берілсін. Олай болса Эйлер теңдеуі 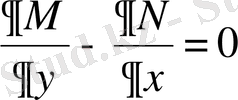немесе 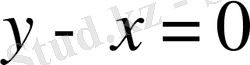түрінде алынады. Бұл кезде бірінші 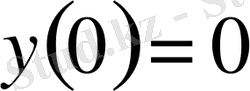шекаралық шарт орындалады, ал екінші 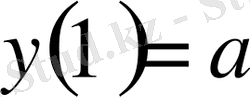шекаралық шарт тек болса ғана орындалады да, қалған 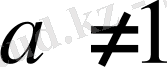жағдайдың бәрінде шекаралық шарттарды қанағаттандыратын экстремал табылмайды.

№ 4 лекция.

Қарапайым 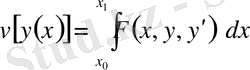функционалының

жекелеген түрлері (жалғасы) .

3) жағдайы.

Бұл кезде интеграл астындағы функциясы тек 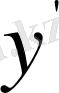туындысына ғана тәуелді. Демек, Эйлер теңдеуі 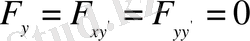болғандықтан 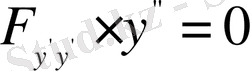түрінде алынады. Осыдан, егер болса, онда оның 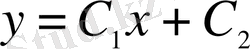шешімі екіпараметрлік түзу сызықтар жинағын береді. Ал, егер 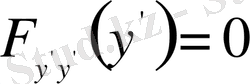болса, онда бұл теңдеудің 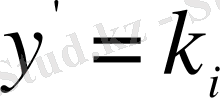немесе 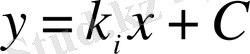түріндегі бір, немесе бірнеше шешімі, құрамында, жоғарыда алынған, 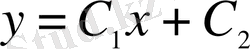шешімі бар, бірпараметрлік түзу сызықтар жинағын береді. Демек, жағдайында функционалдың экстремалдары жалпы жағдайда 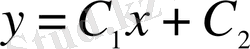түрінде алынады.

4) 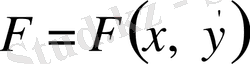жағдайы.

Бұл кезде Эйлер теңдеуі 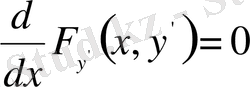түрінде жазылады да, оның бірінше интегралы 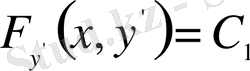теңдеуін береді. Бұл теңдеудің құрамында да айнымалысы болмайды. Бұл теңдеуді туындысына қатысты тікелей шешіп алып интегралдауға, немесе, қосымша көмекші параметр енгізу арқылы интегралдауға болады.

Мысал.

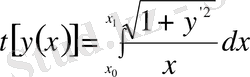түрінде функционал берілсін. Бұл функционал арқылы жазықтықтағы қисығы бойымен бір нүктеден екінші нүктеге жету уақыты анықталады.

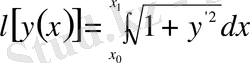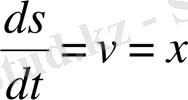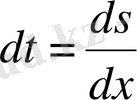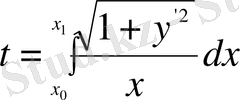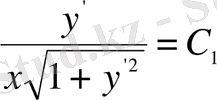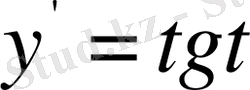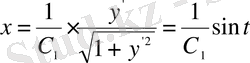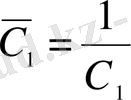Шынында да, жазықтықтағы қисығының доғасының ұзындығы интегралы арқылы анықталатыны белгілі. Егер деп алсақ, онда болады. Демек, . Бұл функционал үшін Эйлер теңдеуінің бірінші интегралы немесе түрінде алынады. Енді түрінде жаңа параметр енгізсек, онда немесе болады. Бұл жерде . Келесі 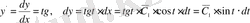түрлендірулер арқылы дифференциалдық

теңдеуін аламыз. Интегралдау арқылы 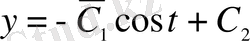алынады.

Демек, , 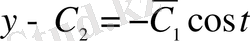. Осыдан параметрін шығарып тастасақ:

Демек, вариациялық есептің шешімі орталығы ордината осінде орналасқан шеңберлер жинағының теңдеулері.

4) жағдайы.

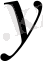Бұл кезде интеграл астындағы функциясы функциясы мен оның 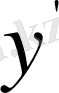туындысына тәуелді. Демек, Эйлер теңдеуі түрінде жазылады. Егер осы теңдеудің барлық мүшелерін 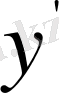шамасына көбейтсек, алынған нәтиже 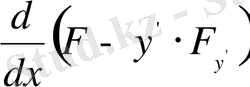толық туындысына тең болатынын көреміз.

Шынында да:

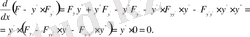
Олай болса Эйлер теңдеуінің бірінші интегралы 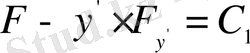теңдеуін береді. Бұл теңдеу айнымалысына айқын түрде тәуелді болмағандықтан, оны туындысына қатысты тікелей шешіп алып интегралдауға, немесе, қосымша көмекші параметр енгізу арқылы интегралдауға болады.

Мысал. Абсцисса осі бойымен айналғанда ауданы ең кіші бет туындататын, екі басы қатаң бекітілген қисықтың теңдеуін табу қажет болсын.

Қисық сызықтың айналуынан туатын беттің ауданы 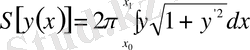формуласымен анықталады. Бұл жерде интеграл астындағы функциясы тек функциясы мен оның туындысына тәуелді. Демек, Эйлер теңдеуінің бірінші интегралы 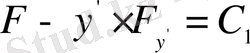түрінде алынады. Берілген есеп жағдайында 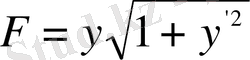және Эйлер теңдеуі 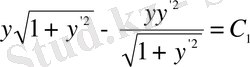түрінде жазылады. Түрлендірулерден кейін 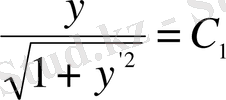теңдеуін аламыз. Бұл теңдеуді 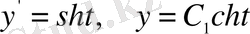алмастыруларын қолданып интегралдаймыз. Келесі 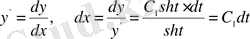түрлендірулерді қолданып 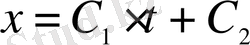және 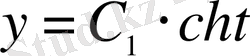шешімін аламыз. Алынған нәтижеден параметрін шығарып тастасақ, онда 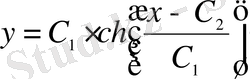шешімін аламыз.

Алынған шешім шынжырлық сызықтардың жинағын береді. Ал олардың абсцисса осі бойымен айналуынан туатын беттер катеноидтар деп аталады. Белгісіз мен параметрлері табылған қисықтың шекаралық нүктелерден өту шарттарынан табылады.

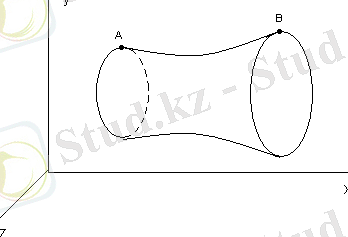
Шекаралық нүктелердің кеңістікте орналасуына байланысты бұл есептің бір, екі шешімі, немесе, бір де бір шешімі болмауы мүмкін.

№ 5 Лекция.

Бір айнымалыға тәуелді бірнеше функцияның және олардың бірінші туындыларының

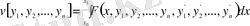функционалдары.

Құрамындағы барлық функциялардың шекаралық шарттары

түрінде берілген

функционалының экстремалын алудың қажетті шарттарын табу үшін белгісіз функциялардың кез келген 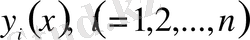біреуін ғана вариациялаймыз да, қалғандарын өзгеріссіз қалдырамыз. Бұл кезде 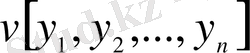функционалы вариацияланатын бір ғана 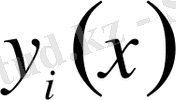функциясының 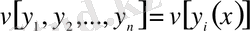функционалына айналады. Демек, экстремум беретін 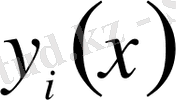функциясы Эйлердің 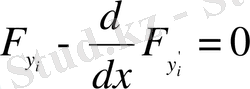теңдеуін қанағаттандыруы тиіс. Бұл жерде индексі 1 мен аралығында кез келген мән қабылдайтын болғандықтан, жалпы жағдайда 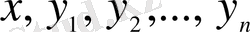кеңістіктігінде берілген вариациялық есептің экстремалдар жинағын анықтайтын 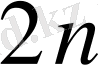параметрлік интегралдық қисықтар жиыны Эйлердің 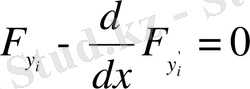дифференциалдық теңдеулер жүйесінің шешімі болады.

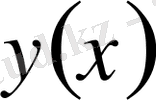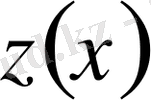Жекелеген жағдайда, егер функционал тек пен функцияларына ғана тәуелді болса, онда вариациялық есеп

функционалының

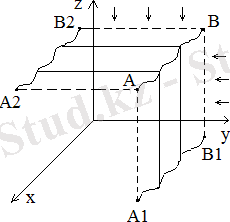
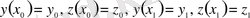шекаралық шарттарын қанағаттандыратын экстремалын табуға қойылады (1-ші сурет) .

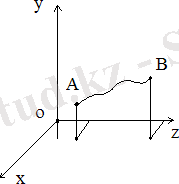
1-ші сурет

Бұл кезде алдымен 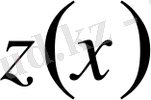функциясы тұрақты деп алынады да, 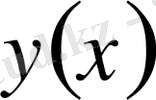функциясы проекциясы жазықтығында өзгермейтіндей етіп вариацияланады.

2-ші сурет

Демек, вариацияланатын қисық әрқашан 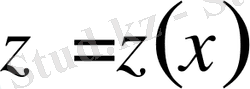цилиндрінің бетінде қалып отырады. Келесі кезекте, дәл осылайша, 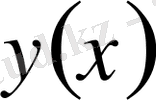функциясы тұрақты деп алынып, 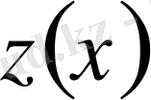функциясы проекциясы жазықтығында өзгермейтіндей етіп вариацияланады. Нәтижесінде Эйлер теңдеулерінің келесі жүйесін аламыз:

Мысал.

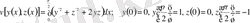
вариациялық есебін шешу керек.

Эйлер теңдеулері былайша жазылады:

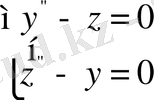Жүйеден 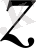функциясын шығарып тастасақ 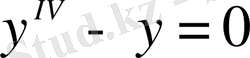теңдеуін аламыз. Төртінші ретті бұл дифференциалдық теңдеудің жалпы шешімі

түрінде алынады. Шекаралық шарттардан 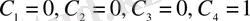екенін анықтаймыз. Демек, функционалға экстремум беретін кеңістіктегі функциялар 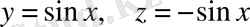түрінде табылады.

№ 6 лекция.

Жоғарғы ретті туындыларға тәуелді функционалдар

Енді 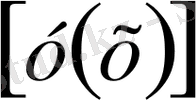= 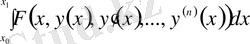түрінде берілген функционалды зерттейік. Бұл жерде функциясы барлық аргументтері бойынша рет дифференциалданатын болсын және шекаралық шарттар мынадай түрде берілсін:

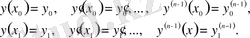
Функционал өзінің экстремумына рет дифференциалданатын қисығында жетеді деп болжайық. Салыстыру қисығы деп аталатын 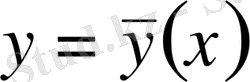қисығы да рет дифференциалданатын болсын.

Функциялардың бір параметрлік

жинағын қарастырайық.

Егер функционал өзінің экстремумына тек қана 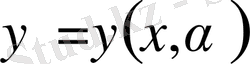жинағының қисықтарында жететін болса, онда бұл функционал параметрінің функциясына айналады да, өзінің экстремумына функционалдың бойынша туындысының мәнінде жетеді. Демек, экстремумға жетудің қажетті шарты 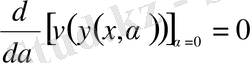түрінде жазылатын болады. Бұл туынды функционалдың вариациясы деп аталады да, арқылы белгіленеді:

Соңғы интегралды 2-ші қосылғыштан бастап бөлшектеп интегралдсақ, онда 2-ші қосылғыш былайша түрленеді:

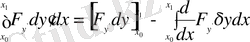
Дәл осылайша 3-қосылғышты екі рет бөліктеп интегралдасақ мынадай нәтиже шығады

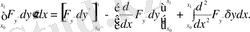
Осы ретпен соңғы -ші қосылғышты рет бөліктеп интегралдасақ:

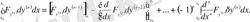
Шекаралық шарттар бойынша функционалдың анықталу аймағының шеткі нүктелерінде 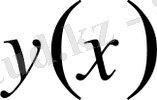функциясы мен оның туындыларының вариациялары нольге тең: 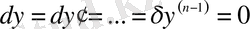. Демек, функционалдың вариациясы былайша анықталады:

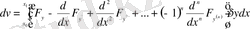
Функционалға экстремум беретін функциясында функционалдың вариациясы болатыны белгілі. Олай болса, негізгі лемманы қолданып мына тепе-теңдікті аламыз:

Демек, экстремум беретін функциясы мына теңдеудің шешімі болады:

Бұл дифференциалдық теңдеу Эйлер-Пуассон теңдеуі деп аталады. Ал, оның интегралдық қисықтары вариациялық есептің экстремалдары деп аталады.

Мысал.

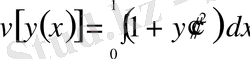Equation. 3 функционалының экстремалы

шекаралық шарттардан анықталсын.

Эйлер-Пуассон теңдеуі 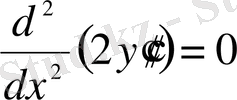түрінде жазылып, 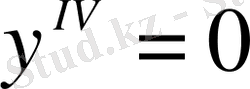түрге келеді. Алынған 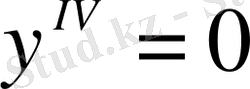дифференциалдық теңдеудің жалпы шешімі 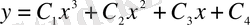түрде алынады. Шекаралық шарттардан белгісіз тұрақтылардың 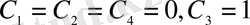болатынын анықтаймыз. Демек, дифференциалдық теңдеудің шешімі түзуі түрінде алынады.

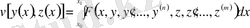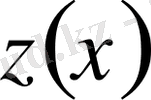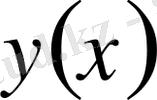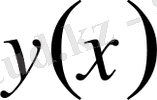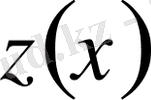Егер функционал түрінде берілсе, онда функциясын өзгеріссіз қалдырып функциясын вариациялаймыз. Бұл кезде функционалға экстремум беретін және функциялары келесі Пуассон теңдеуін қанағаттандыруы керек:

Сол сияқты, 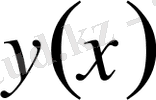функциясын тұрақты сақтап, 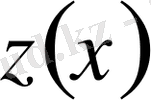функциясын вариацияласақ, Эйлер-Пуассон теңдеуі былайша жазылады.

Осылайша алынған теңдеулер жүйесін шешу арқылы экстремалдық беттен 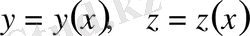өрнектерін аламыз.

Жалпы жағдайда, функциялар саны екіден көп болса

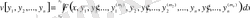
функционалының экстремумын табу үшін кез-келген 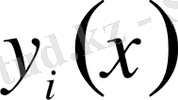функциясын вариациялап, қалған функцияларды өзгертпей қалдыру арқылы Эйлер-Пуассон теңдеулерінің келесі жүйесін аламыз:

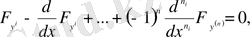
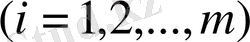№ 7 лекция.

Бірнеше тәуелсіз айнымалылардың функцияларының

функционалдары.

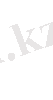
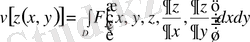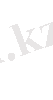
функционалын экстремумға зерттейік. Вариациялық есепте 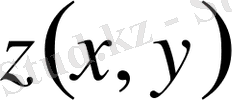функциясының аймағының шекарасындағы мәндері, демек, барлық мүмкін беттер өтетін кеңістіктегі контуры берілген. Жазбаларды қысқарту үшін мынадай 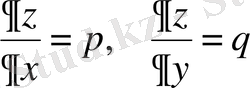белгілеулерді енгізейік. Интеграл астындағы функциясы үш рет, ал экстремум беретін беттің 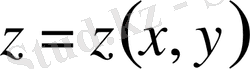функциясы екі рет дифференциялданатын болсын. Енді, тағы да бір параметрлік 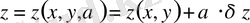беттер жинағын қарастырамыз. 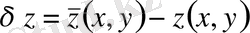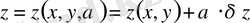Бұл жерде , ал функциясы параметрінің мәнінде экстремум беретін функциясын, ал мәнінде кез келген бір 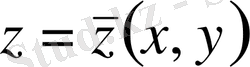салыстыру бетін береді. Демек, 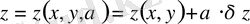жинағында функционал параметрінің функциясына айналады. Бұл функцияның болғанда экстремумға жету шарты былайша жазылады:

Бұл туындыны функционалының вариациясы деп атап, арқылы белгілейді. Туындыны ашып жазсақ:

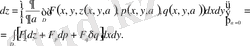
Бұл жерде

Бірақ

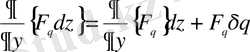
болғандықтан, алынған нәтижені өзара қосып интегралдасақ

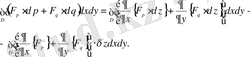
Бұл жерде 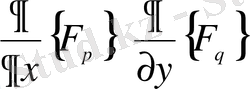шамалары пен бойынша алынған толық дербес туындылар деп аталады. Мысалы: 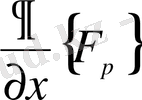есептелінгенде тұрақты деп есептеліп, бойынша туынды алынады:

Енді тұрақты деп есепеп, бойынша туынды алсақ:

Енді белгілі 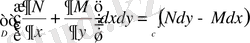Грин формуласын қолдансақ

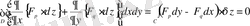теңдігін аламыз.

Соңғы интеграл нолге теңеседі, себебі барлық мүмкін беттер кеңістіктегі контуры арқылы өтетін болғандықтан контурында функционалдың вариациясы нолге тең болады. Демек, 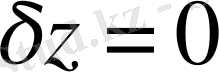болады да, соңғы интеграл нолге айналып кетеді. Олай болса

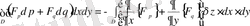Сонымен, функционалдың вариациясының

шарты енді былайша түрге енеді

Экстремалдык беттің варияциясы еркін таңдалады, оған тек үздіксіз болу, дифференциялдану және контурында нолге айналу шарттары қойылады. Ал, бірінші көбейткішке вариациялық есептеудің негізгі леммасын қолдансақ

болуы керек.

Демек, экстремалдық 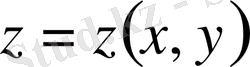функциясы дербес туындылы, екінші ретті дифференциалдық теңдеудің шешімі болады. Бұл теңдеу Остроградский теңдеуі деп аталады.

1-ші мысал:

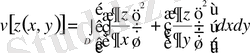
функционалы үшін Остроградский теңдеуін алайық. Функционалға экстремум беретін 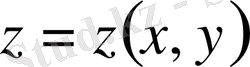функциясының аймағының контурындағы мәні 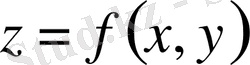белгілі. Бұл жерде интеграл астындағы функция 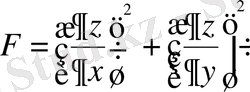түрінде берілген. Енді Остроградский теңдеуінің құрамындағы шамаларды есептейік:

Алынған мәндерді Остроградский теңдеуіне қойсақ, дербес туындылы, екінші ретті біртекті дифференциалдық теңдеу аламыз:

Бұл теңдеу Лаплас теңдеуі деп аталады. Лаплас теңдеуінің контурындағы шекаралық шартқа сәйкес болатын үздіксіз шешімін табу математикалық физика ғылымындағы негізгі есептердің бірі. Бұл есеп Дирихле есебі деп аталады.

2 -ші мысал:

Енді функционал

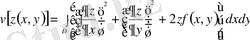
түрінде берілсін. Функционалға экстремум беретін 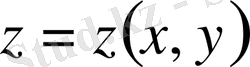функциясының аймағының контурындағы мәні 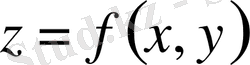белгілі. Бұл жерде интеграл астындағы функция 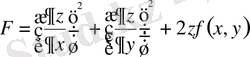түрінде берілген. Бұл кезде Остроградский теңдеуі