Анықталған интегралдың қолданылуы: жазық фигуралардың ауданын есептеу (функциялық, параметрлік және полярлық әдістер)


АнықТАЛҒАН ИНТЕГРАЛДЫҢ ҚОЛДАНЫЛУЛАРЫ
§ 7. 21 Жазық фигураның ауданы
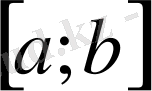 кесіндісінде үзіліссіз оң функция берілсін, яғни
кесіндісінде үзіліссіз оң функция берілсін, яғни
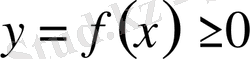 ,
,
сонда осы қисықтың графигімен, абсцисса осімен және екі бүйірінен
x=a
,
 түзулерімен шенелген қисық сызықты трапецияның ауданы
түзулерімен шенелген қисық сызықты трапецияның ауданы
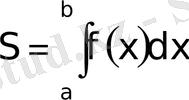 (21)
(21)
формуласымен табылады. Егер функция
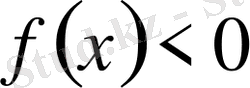 , яғни қисық
0х
осінің төменгі жағынан өтетін болса, онда фигураның ауданы мына формуламен табылады
, яғни қисық
0х
осінің төменгі жағынан өтетін болса, онда фигураның ауданы мына формуламен табылады
у
0 a b х
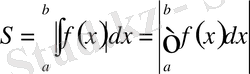 .
.
Егкр
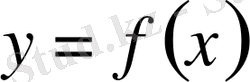 функциясы ауыспа таңбалы болса, онда оң және теріс аудандарды жеке-жеке есептеп алынған нәтижелерді қосады:
функциясы ауыспа таңбалы болса, онда оң және теріс аудандарды жеке-жеке есептеп алынған нәтижелерді қосады:
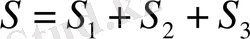 .
.
у
s 1 s 3
0 a b х
s 2
Егер фигура жоғарыдан y=f 2 (x) және төменнен y=f 1 (x) функцияларының графиктерімен, ал екі бүйірінен x=a, x=b түзулерімен шенелсе, онда оның ауданы
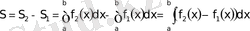
теңдігі арқылы табылады.
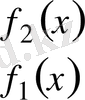 у
у
0 a b
Мысалдар. 1
.
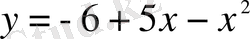 және абсцисса осімен қоршалған фигураның ауданын табу керек.
және абсцисса осімен қоршалған фигураның ауданын табу керек.
y
0 2 3 x
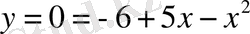 ;
;
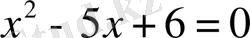 ;
;
 ;
;
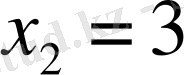 ;
;
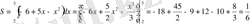 кв. бірлік.
кв. бірлік.
2.
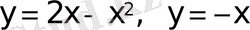 сызықтарымен қоршалған фигураның ауданын табу керек.
сызықтарымен қоршалған фигураның ауданын табу керек.
Қисықтардың өзара қиылысу нүктелерін және олардың абсцисса осімен қиылысу нүктелерін табамыз.
y
s 1
0 1 2 3 x
s 2
s 3
y=-x
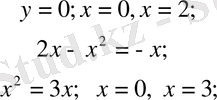 Equation. 3
Equation. 3
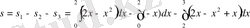 Equation. 3 .
Equation. 3 .
Ой толғау. Автор аспирантурада оқып жүрген кездері параллель қисықтар ұғымын енгізді, осыны келтірелік.
Егер абсциссалары бірдей нүктелерге жүргізілген жанамалары параллель болса, онда ондай қисықтар параллель деп аталады.
у
h
0 a b х
«Қисық сызықты» тік төртбұрыштың ауданын дәлелдеңдер:
S=h(b-a) .
Параллель беттер ұғымын енгізуге бола ма (енгізіңдер ???) .
7. 21. 1 Параметрлік теңдеулерімен берілген фигураның ауданы. Қисық параметрлік теңдеулерімен берілсін:
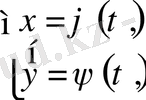
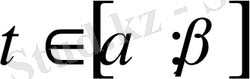 , және
ϕ(α) =а, ϕ(β) =b.
, және
ϕ(α) =а, ϕ(β) =b.
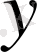 - үзіліссіз функция,
- үзіліссіз функция,
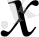 және оның туындысы
ϕ′(t )
-үзіліссіз функциялар болсын. (21) формуланы пайдаланамыз:
және оның туындысы
ϕ′(t )
-үзіліссіз функциялар болсын. (21) формуланы пайдаланамыз:
 .
.
Мысал.
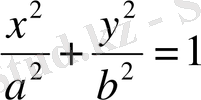 эллипсімен шенелген фигураның ауданын табу керек. Эллипстің
0х
осінің үстінде орналасқан бөлігінің ауданын тауып екі еселейміз:
эллипсімен шенелген фигураның ауданын табу керек. Эллипстің
0х
осінің үстінде орналасқан бөлігінің ауданын тауып екі еселейміз:
 y
y
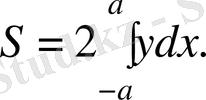
Эллипстің параметрлік теңдеуін аламыз:
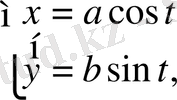 t- бұрыш
t- бұрыш
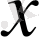
 мен
мен
 -ның арасында өзгереді, онда
-ның арасында өзгереді, онда
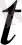
 -ден 0-ге дейін өзгереді, эллипстің тек жоғарғы бөлігі ғана қарастырылады.
-ден 0-ге дейін өзгереді, эллипстің тек жоғарғы бөлігі ғана қарастырылады.
 ;
;
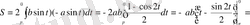
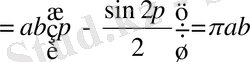 ,
,
S элл =πab.
7. 21. 2 Полярлық координаталарымен берілген фигураның ауданы. Полярлық координаталарымен берілген қисықты қарастырамыз. Қисық және полярлық бұрышы
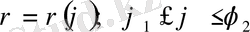
теңдеулерімен берілген фигураның ауданын табалық.
Анықтама . ρ=ρ(φ) функциясы [φ 1 , φ 2 ] аралығында үзіліссіз, әрі теріс болмасын. Полярлық осьпен жасайтын бұрыштары φ 1 және φ 2 болатын екі полярлық радиустар және ρ(φ) қисығымен шенелген фигура қисық сызықты сектор деп аталады.
 бұрышын
бұрышын
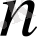 бөлікке бөлеміз.
бөлікке бөлеміз.
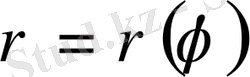
 2
2
ϕ 1
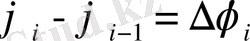 - мен белгілейміз. Осы бұрыштың ішінен бір
ξ
i
бұрышын аламыз:
- мен белгілейміз. Осы бұрыштың ішінен бір
ξ
i
бұрышын аламыз:
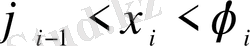 және қисық бойынан кез келген
және қисық бойынан кез келген
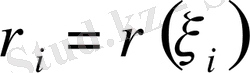 нүктесін аламыз.
нүктесін аламыз.
Анықтама.
Полярлық радиустармен және
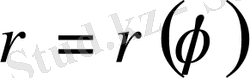 қисығымен қоршалған фигураның ауданы деп ең үлкен
∆ϕ
i
→
0
-дағы дөңгелек сызықты секторлардың аудандарының қосындысын айтады:
қисығымен қоршалған фигураның ауданы деп ең үлкен
∆ϕ
i
→
0
-дағы дөңгелек сызықты секторлардың аудандарының қосындысын айтады:
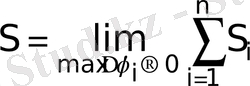 . (*)
. (*)
Бұл дөңгелек сектордың
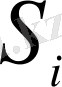 ауданын анықтайық:
ауданын анықтайық:
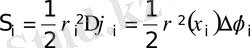 .
.
(*) қосындысы интегралдық, өйткені ол төменнен және жоғарыдан Дарбу қосындысымен шенелген, сондықтан оның шегі
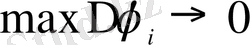 болғанда бар, яғни
болғанда бар, яғни
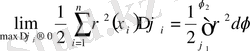 .
.
Сонымен, фигураның ауданы мына формуламен табылады:
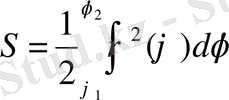 . (22)
. (22)
Мысалдар. 1. Полярлық координаталарымен берілген дөңгелектің ауданын табалық.


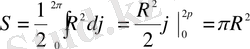 .
.
2.
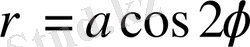 төрт жапырақты розамен шектелген фигураның ауданын табалық.
төрт жапырақты розамен шектелген фигураның ауданын табалық.


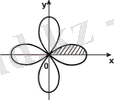

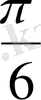
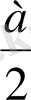
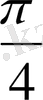

Жапырақтың жартысының ауданын табамыз, яғни төрт жапырақты розаның сегізден бір бөлігінің ауданын табамыз:
 ,
,
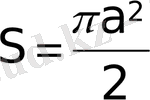 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz