Теңдеулерді құруға арналған есептер

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 3

І. ҚАРАПАЙЫМ ШАРТТЫ ЕСЕПТЕР

1.1 Концентрация мен процентке қатысты есептерді шешу әдістері ... ... ... ... ... ... ... ... ... ... ... ... ... ... .5

1.2 «Қозғалыс» . қа арналған есептер ... ... ... ... ... .20

1.3 Айнымалылылар саны теңдеулер санынан
көп болатын есептер ... ... ... ... ... ... ... ..31

ІІ. КҮРДЕЛІ ШАРТТЫ ЕСЕПТЕР

2.1 Теңсіздіктер көмегімен шешілетін есептер ... ... ... ...37

2.2 Бүтін белгісізі бар есептер ... ... ... ... ... ... ...42

2.3 Балама шарты бар есептер ... ... ... ... ... ... ... ...47

2.4 Функцияның үлкен және кіші мәнін анықтауға арналған есептер ... .

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ...64

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... .. 65

Теңдеулер құруға арналған есептер немесе алгебралық мәсел есептер элементар математика бір бөлімін құрайтындығы белгілі. Мұндай есептерді шешу оқушылардың логиялық ойлау шеберлігін және ғылыми қөзқарасын дамытуға үлкен септігін тигізеді.
Теңдеулер құруға арналған есептер элементар математиканың көптеген оқулықтарында кездеседі. Мысалы [1]-[6].
Бұл диплом жұмысында теңдеулер құруға арналған есептер қарастырылады.
Дипломдық жұмысым ІІ тараудан тұрады.
Қарапайым шартты есептер – деп аталатын бірінші тарауда, концентрация, «қозғалыс» және теңдеулер санынан айнымалылар саны көп есептер қарастыралады. Бұл есептердің шарттары қарапайым болғандықтан, онда әртүрлі мүмкін жағдайларды қарастырудың қажеті жоқ.
Күрделі шартты есептер - деп аталатын еінші тарауда теңсіздіктер көмегімен, алтернативті шартты және функцияның ең үлкен және ең кіші мәнін табуға арналған есептер қарастырылады. Бұл тараудағы есептер күрделі шартты болып келеді, себебі мұндай есептерді шешу үшін әртүрлі мүмкін жағдайлар қарастырып, соның ішінде есептің шартын қанағаттандыратын жағдайды алу қажеттілігі туындайды. Мысалы келесі есепті қарастырайық.
Есеп. Дойбашылардың А және В екі командасы жарысқа қатысуда. Жарыстың шарты бойынша, әрбір команданың ойыншысы екінші команданың ойыншысымен бір партия ойнайды. Жалпы ойындардың саны екі командадағы ойыншылардың санынан төрт есе артық болу керек еді. Алайда екі ойыншы ауырып қалуына байланысты, жарысқа қатыса алмай қалды. Сондықтан ойын саны жоспарланғанан 17 – ге аз болды. А командасы үшін жарысқа неше ойыншы қатысқандығын анықтаңыз, егер ондағы дойбашылар саны В командасындағы дойбашылар санынан аз болғандығы белгілі болса.

1. М.В. Лурье, Б.И. Александров. Задачи на составление уравнений. Москва: Наука.1990. 3-е издание.
2. В.С. Крамор. Задачи на составление уравнений и методы их решения. Москва: «Мир и образование».2009.
3. В.С. Крамор, К.Н. Лунгу. Повторяем и систематизируем школьный курс алгебры. Москва, 2001.
4. В.М. Максимов. Пособие по математике для поступающих в МГУ. М.: Наука. 1972.
5. Б. И. Александров, М. В. Лурье, В.М. Максимов. Пособие по подготовке к писменному экзамену математике В МГУ. М: Наука.1972.
6. В.С. Крамор. Готовимся к экзамену по математике. М: ««Мир и образование».2006.
7. Қазақша-орысша, орысша-қазақша терминологиялық сөздік: Жалпы
редакциясын басқарған А.Құсайинов.-Алматы:”Рауан ”, 1999.

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 63 бет
Таңдаулыға:

Мазмұны

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ..3

І. ҚАРАПАЙЫМ ШАРТТЫ ЕСЕПТЕР

1.1 Концентрация мен процентке қатысты есептерді шешу
әдістері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
... ... ... ... ... ... ... ... ... ... ...5

1.2 Қозғалыс - қа арналған
есептер ... ... ... ... ... ... ... ... ... ... ... ... .20

1.3 Айнымалылылар саны теңдеулер санынан
көп болатын
есептер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
... ... ... ..31

ІІ. КҮРДЕЛІ ШАРТТЫ ЕСЕПТЕР

2.1 Теңсіздіктер көмегімен шешілетін
есептер ... ... ... ... ... ... ... ... ..37

2.2 Бүтін белгісізі бар
есептер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
42

2.3 Балама шарты бар
есептер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..4 7

2.4 Функцияның үлкен және кіші мәнін анықтауға арналған
есептер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
... ... ... ... ... ... ... ... ... ... .56

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... 64

ҚОЛДАНЫЛҒАН
ӘДЕБИЕТТЕР ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
65

Кіріспе

Теңдеулер құруға арналған есептер немесе алгебралық мәсел есептер
элементар математика бір бөлімін құрайтындығы белгілі. Мұндай есептерді
шешу оқушылардың логиялық ойлау шеберлігін және ғылыми қөзқарасын дамытуға
үлкен септігін тигізеді.

Теңдеулер құруға арналған есептер элементар математиканың көптеген
оқулықтарында кездеседі. Мысалы [1]-[6].

Бұл диплом жұмысында теңдеулер құруға арналған есептер қарастырылады.

Дипломдық жұмысым ІІ тараудан тұрады.

Қарапайым шартты есептер – деп аталатын бірінші тарауда, концентрация,
қозғалыс және теңдеулер санынан айнымалылар саны көп есептер
қарастыралады. Бұл есептердің шарттары қарапайым болғандықтан, онда әртүрлі
мүмкін жағдайларды қарастырудың қажеті жоқ.

Күрделі шартты есептер - деп аталатын еінші тарауда теңсіздіктер
көмегімен, алтернативті шартты және функцияның ең үлкен және ең кіші мәнін
табуға арналған есептер қарастырылады. Бұл тараудағы есептер күрделі шартты
болып келеді, себебі мұндай есептерді шешу үшін әртүрлі мүмкін жағдайлар
қарастырып, соның ішінде есептің шартын қанағаттандыратын жағдайды алу
қажеттілігі туындайды. Мысалы келесі есепті қарастырайық.

Есеп. Дойбашылардың А және В екі командасы жарысқа қатысуда. Жарыстың шарты
бойынша, әрбір команданың ойыншысы екінші команданың ойыншысымен бір партия
ойнайды. Жалпы ойындардың саны екі командадағы ойыншылардың санынан төрт
есе артық болу керек еді. Алайда екі ойыншы ауырып қалуына байланысты,
жарысқа қатыса алмай қалды. Сондықтан ойын саны жоспарланғанан 17 – ге аз
болды. А командасы үшін жарысқа неше ойыншы қатысқандығын анықтаңыз, егер
ондағы дойбашылар саны В командасындағы дойбашылар санынан аз болғандығы
белгілі болса.

Шешуі. А және В командалары үшін ойынға қатысқан дойбашылар санын
сәйкесінше және деп белгілейік .
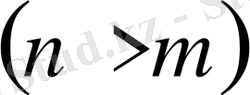Жоспарланған ойындар саны болатындығы түсінікті. Сонда есептің
бірінші шартынан

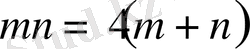
теңдеуін аламыз. Ал екінші теңдеуді бірден жазу мүмкін емес, себебі ауырып
қалған ойыншылар қай командаға тиесілі екені белгісіз. Келесі үш жағдай
болуы мүмкін:

1) егер А командасының ойыншылары ауырып қалса, онда

;

2) егер А командасының ойыншылары ауырып қалса, онда

;

3) егер әрбір командадан бір ойыншыдан ауырып қалса, онда

.

Яғни берілген есептің шешімін анықтау үшін, осы мүмкін жағдайлардың қайсысы
есептің шартын қанағаттандыратындығын анықтау керек.

Қорыта айтқанда, бұл диплом жұмысын мектеп оқушыларына мәсел
есептерді шешуді үйрету үшін көмекші құрал ретінде пайдалануына болады.

І. ҚАРАПАЙЫМ ШАРТТЫ ЕСЕПТЕР

1.1 Концентрация мен процентке қатысты есептерді шешу әдістері.

Концентрация мен процентке қатысты есептерді шешкенде, әртүрлі
қоспаларды, қортпаларды және ерітінділерді алу есептері қарастырылады.
Мұндай есептерді шешу үшін, төмендегі негізгі ұйғарымдар орындалады
деп есептелінеді:
а) барлық алынған қорытпалар мен ерітінділер біртекті деп есетелінеді;
б) көлемдері және болатын екі қортпаны біріктіргенде, пайда
болатын ерітіндінің көлемі, олардың көлемдерінің қосындысына тең болады,
яғни

. (1.1.1)

Келесі жайтты ескере кеткен жөн. Негізінде, физикалық тұрғыдан, екі
қоспадан ерітінді алғанда, пайда болған ерітіндінің көлемі, олардың
көлемдерінің қосындысына тең бола бермейді.
Нақтылық үшін, 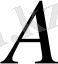, 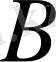және - үш компоненттен тұратын
қортпаны қарастырайық.Сонда ерітіндінің көлемі (1.1.1) бойынша келесі түрде
анықталады:

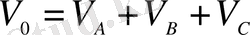, (1.1.2)

ал

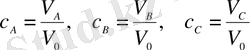(1.1.3)

әрбір компоненттің көлемі, толық көлемнің қандай бөлігін құрайтындығын
көрсетеді және

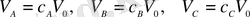(1.1.4)

Ерітіндідегі әрбір компоненттің көлемінің, ерітіндінің толық көлеміне
қатынасы

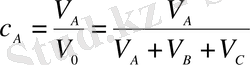(1.1.5)

компоненттің көлемдік концентрациясы деп аталады.

Концентрация – ол өлшемсіз шама. Ерітіндіні құрайтын барлық
компоненттердің концентрациясының қосындысы бірге тең, яғни

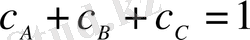. (1.1.6)

Сондықтан, компоненттен тұратын ерітіндінің құрамын анықтау үшін,
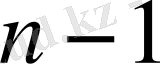компоненттің концентрациясын білу жеткілікті.
Егер ерітіндіні құрайтын компоненталардың концентрациялары белгілі
болса, онда ерітіндінің әрбір компонентасының көлемін келесі түрде схема
1 анықтауға болады

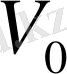
және
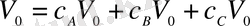. (1.1.7)

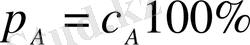(1.1.8)

шамасы 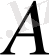компонентасының проценттік мөлшері деп аталады.
Егер 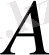заттының проценттік мөлшері белгілі болса, онда оның
концентрациясы келесі формуламен анықталады:

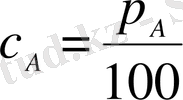. (1.1.9)

Мысалы, 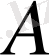затының проценттік мөлшері 70% болса, онда оның
концентрациясы 0,7 - ге тең, ал 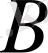затының проценттік мөлшері 10% болса,
онда оның концентрациясы 0,1 - ге тең және т.с.с.
Тура осы сияқты, ерітіндідегі компоненталардың салмақтық
концентрациясын анықтауға болады, яғни

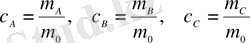(1.1.10)

және мұнда да

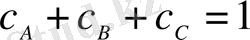, (11)

мұндағы 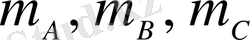- әрбір компонентаның салмағы, ал 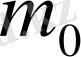- ерітіндінің жалпы
салмағы.
Көбіне, қарастырылып отырған есептерде құрамында
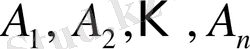компоненттерінің біреуі немесе бірнешесі болатын қоспалардан белгілі бір
қатынас құрайтын жаңа ерітінді алу керек. Сонымен қатар, кейбір есептерде
алынған ерітіндегі 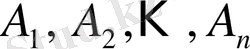салмақтық немесе концентрациялық мөлшерін алу
қажет.
Мұндай есептерді шешкенде, ерітіндінің көлемдік немесе салмақтық
концентрациясын енгізген ыңғайлы, яғни формулада көрсетілгендей әрбір
компонентаға ыдыратқан жөн. Сонан соң, есептің шарттарын
қанағаттандыратын жаңа ерітіндіні алу керек. Бұл жағдайда
әрбіркомпонентаның мөлшерін анықтау оңай болады.
Жоғарыдағы айтылғандарды ескере отырып, келесі мысалдарды
қарастырайық.
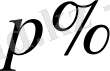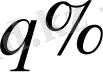Есеп 1. Әрбірінде мыстың проценттік мөлшері және болатын, мыс
пен цинктен тұратын екі түйір қорытпа берілген. Проценттік мөлшері
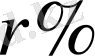болатын ерітінді алу үшін, екі қортпаны қандай мөлшерде алу керек?
Шешуі. Бұл есепті шешу келесі схема 2 бойынша жүзеге асырылады.
Бірінші қоспадағы мыстың концентрациясы 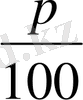, ал екіншісінде .

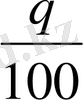Егер бірінші қортпадан х кг, ал екінші қортпадан y кг алсақ, онда

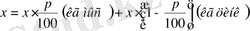
және

.

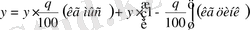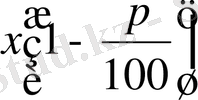
Алынған қоспада мыстың мөлшері:

,

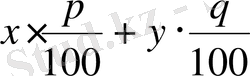ал бұл қоспаның жалпы салмағы 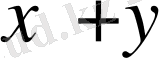кг. Сондықтан, анықтамаға сәйкес,
қоспадағы мыстың концентрацисы келесі өрнекпен анықталады:

.

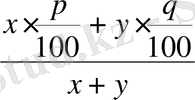Есептің шарты бойынша, бұл концентрация 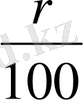болуы керек. Сондықтан:

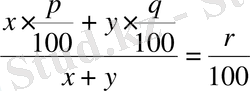
немесе

.

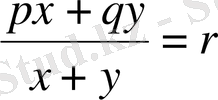Алынған теңдеуді шешейік. Бұл теңдеу екі айнымалыдан тұрады. Сондықтан
олардың әрқайсысын табу мүмкін емес. Бірақ есептің шартында оларды табу
талап етілмейді, яғни олардың қатынасын табу керек. Сонда:

.

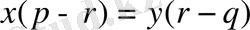Мүмкін болатын жағдайларды қарастырайық.

1) .

Бұл жағдайда барлық кортпалардың концентрациялары бірдей, сондықтан есептің
шексіз көп шешімі болады. Физикалық мағынасы: бірінші және екінші қоспадан
қалағанымызша алуға болады.

2) .

Бұл жағдайда теңдеу келесі түрге келеді

,

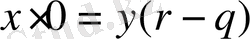яғни 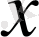- кез-келген, ал . Алынған нәтиженің физикалық мағнасы
келесі: егер алынуға тиіс қоспаның концентрациясы бірінші қоспаның
концентрациясымен сәйкес келсе, бірақ екінші қоспаның концентрациясымен тең
болмаса, онда бірінші қоспадан қалаған мөлшерде алып, ал екінші қоспадан
алмай-ақ қойсақ болады дегенді білдіреді.

3) .

Бұл жағдайда теңдеу келесі түрге келеді

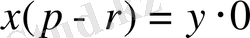
Мұнда 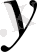- кез-келген, ал . Физикалық мағнасы алдыңғы жағдайға
ұқсас.

4) .

Бұл жағдайда, 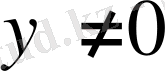болғандықтан, теңдеуді келесі түрде жазуға болады:

.

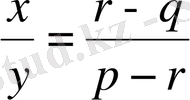Бұл теңдеудің шешімі болады, егер 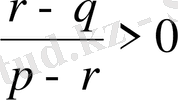болса.
Қарастырылып мысал қарапайым болғанымен, ол қоспаларға қатысты есепті
шешудің негізгі әдісін меңгеруге мүмкіндік береді.

Есеп 2. Үш бірдей ыдыстың ортасына дейін спирттік ерітінділер құйылған.
Үшінші ыдыстағы ерітіндіні бірінші және екінші ыдыстарға теңдей бөліп
құйғанда, бірінші ыдыстағы спирттің көлемдік концентрациясы бастапқыдан 20%
азайды, ал екінші ыдыстағы спирттің көлемдік концентрациясы бастапқыдан 10%
көбейді. Бастапқыда, бірінші ыдыстағы спирттің мөлшері екіншісінен неше есе
артық болғанын анықтаңыз?
Шешуі. Ыдыстардың көлемі бірдей болғандықтан, олардың жартысының көлемін
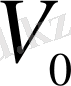- деп белгілеп алайық және әрбір ыдыстағы спирттің бастапқы
концентрациясы сәйкесінш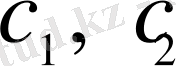е және 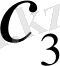болсын. Сонда бірінші ыдыстағы
бастапқы спирттің мөлшері 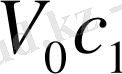, екіншісінікі 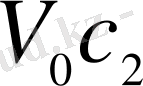, ал үшіншісінікі .
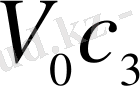сурет 1 көрсетілген.
Есепті шешу үшін, үшінші ыдыстағы спирттік ерітінді бірінші және
екінші ыдыстарға теңдей бөліп құйғанда, бірінші және екінші ыдыстағы
спирттік ерітінділердің мөлшерін есептейік:
бірінші ыдыста

,

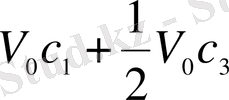екінші ыдыста

.

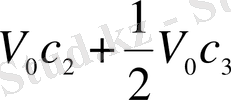Бірінші және екінші ыдыстардағы пайда болған спирттік ерітінділердің
концентрациясын анықтайық. Сонда бірінші ыдыстағы спирттік ерітіндінің
концентрациясы:

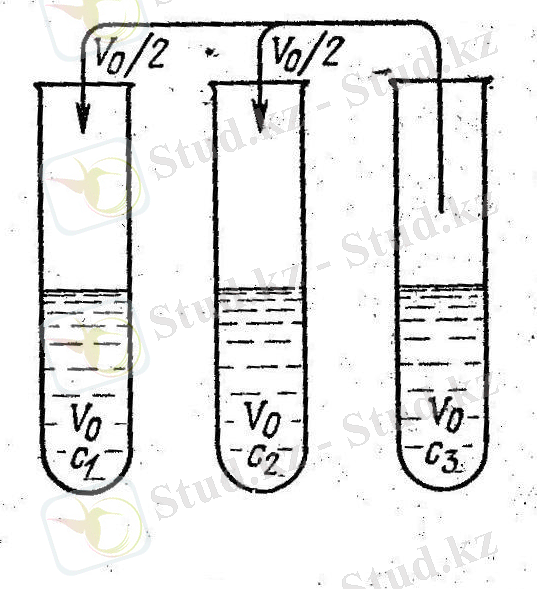
сурет 1

,

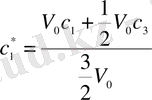ал екіншісінікі

.

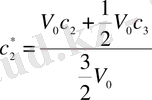Есептің шарты бойынша 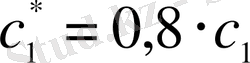және 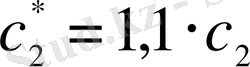. Сондықтан үш айнымалысы бар екі
теңдеулер жүйесін аламыз:

,

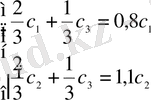немесе

.

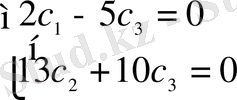Бұл теңдеулер жүйесінен де, алдыңғы есеп сияқты 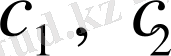және мәндерін
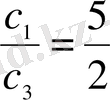табу мүмкін емес. Бірақ теңдеулер жүйесінен және
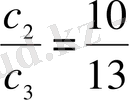қатынастарын табуға болады. Сондықтан

,

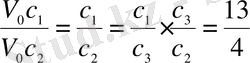яғни есептің жауабы:.
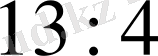Енді процессті бірнеше рет қайталағанда, есептің шешімінің белгілі бір
заңдылыққа бағынатын көрсетейік. Ол үшін келесі есепті қарастырайық.
Есеп 3. Көлемі 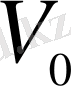литр болатын ыдысқа 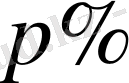-ты тұз ерітіндісі бар.
Ыдыстан -литр ерітінді төгіліп, орнына -литр таза су құйылады
(сурет 2). Бұл процесс рет қайталанады. Ыдыстағы тұздың
концентрациясы қандай заңдылықпен өзгереді?
Шешуі. Бастапқы кезде ерітіндідегі тұз мөлшері

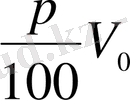
тең екіндігі түсінікті. Ыдыстан -литр ерітінді төгіліп тасталғанан
кейін, ыдыста

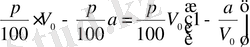
тұз қалады. Ал, -литр таза су құйғанда, оның концентрациясы

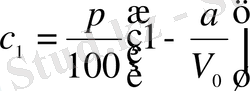
болады.

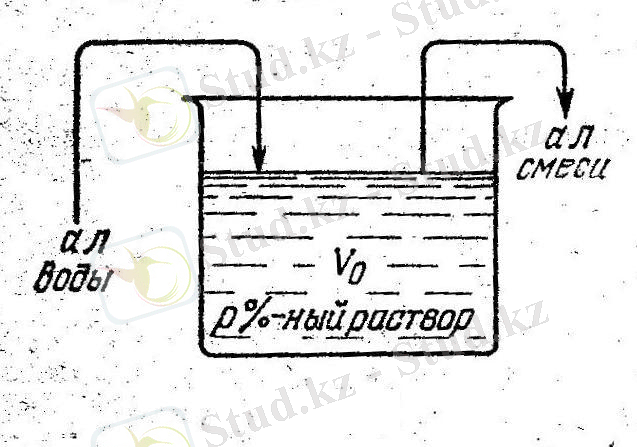
сурет 2

Ыдыстан тағы да -литр ерітінді төгіліп тасталғанда, ондағы тұз
мөлшері

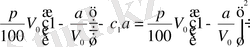
тең, ал -литр таза су құйылғанда оның концентрациясы

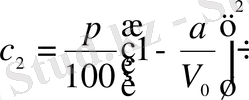
болады. Енді процесті рет қайталағанда ыдыстағы тұздың концентрациясы

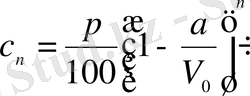(1.1.12)

болатындығын көруге болады, мұндағы

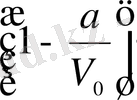
көбейткіші тұз концентрациясының калай өзгеретіндігін көрсетеді.
Осы есепке ұқсас келесі мысалдарды қарастырайық.
Мысал 1. Көлемі 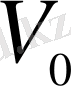болатын ыдыстан -литр ерітінді төгіліп, орнына
-литр таза су құйылады. 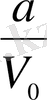шамасы белгілі болсын. Процессті неше
рет жалғастырғанда, ыдыстағы тұз концентрациясы к есе азаяды?
Шешуі. Жоғарыда табылған (12) формуланы пайдаланайық, сонда

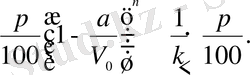
Бұдан

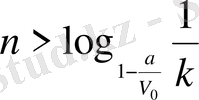
екендігін анықтаймыз.
Мысал 2. Көлемі 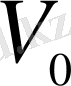болатын ыдыстан -литр ерітінді төгіліп, орнына
-литр таза су құйылады. Процессті рет жалғастырғанда, ыдыстағы
тұз концентрациясы к есе азайғандығы белгілі. - 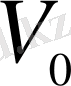көлемінің қанша
бөлігін құрайтындығын анықтаңыз?
Шешуі. (1.1.12) формула бойынша

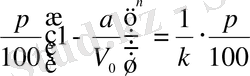
немесе

.

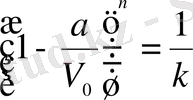Соңғы теңдіктен:

.

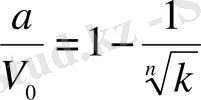Мысал 3. Көлемдері 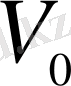болатын екі бірдей ыдысқа, концентрациясы бірдей
қышқыл құйылған. Бірінші ыдыстан -литр ерітінді төгіліп, орнына -
литр таза су құйылады және бұл процессті тағы бір рет қайталайды. Екінші
ыдыстан 2-литр ерітінді төгіліп, орнына 2-литр таза су құйылады
және бұл процессті тағы бір рет қайталайды. Бірінші ыдыстағы қышқыл
концентрациясы екінші ыдыстағы қышқыл концентрацисына қарағанда 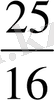есе
көп екендігі белгілі болса, онда литр ыдыс көлемінің қандай бөлігін
құрайтындығын анықтаңыз?
Шешуі. 3 есеп нәтижелерін пайдаланайық. Сонда

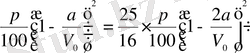
немесе

.

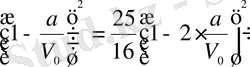Соңғы теңдіктен 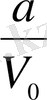қатынасын анықтайық. Теңдіктің екі жағынан түбір
алсақ

.

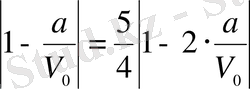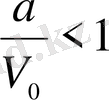және 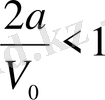болғандықтан

.

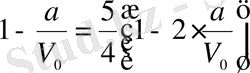Онда

.

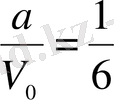Ескерту. Теңдіктің екі жағынан түбір алғанда

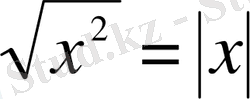
формуласы қолданылған.
Көлемі 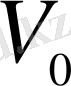болатын ыдыстан -литр ерітінді төгіліп, орнына
концентрацисы 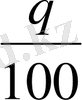болатын -литр ерітінді құйылғанда, ыдыстағы тұз
мөлшерінің өзгеруін анықтайық, яғни (1.1.12) формуланың жалпыланған түрін
жазайық.
Процесті рет жалғастырғанда, ыдыстағы тұз концентрациясы
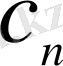болсын. Сонда

.

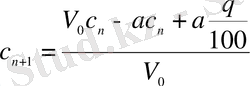немесе

.

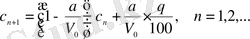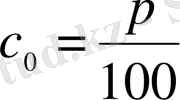екенін ескере отырып, соңғы қатынастан мәнін анықтайық:

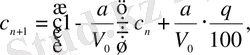
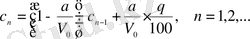
Бірінші теңдіктен екінші теңдікті алып тастасақ, онда

.

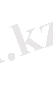
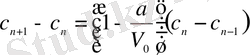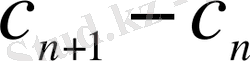айырымын 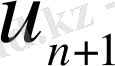, ал 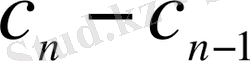айырымын 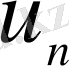арқылы белгілеп алсақ:

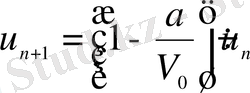
немесе

.

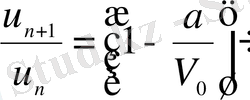Соңғы қатынастан 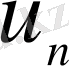тізбегі геометриялық прогрессия құратындығы шығады.
Сондықтан

.

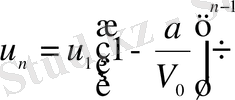Бұл геометриялық прогрессия алғашқы мүшесін

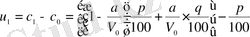
теңдігінен анықтауға болады, яғни

.

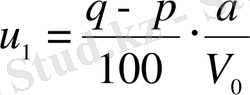Бұдан

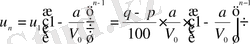
немесе

.

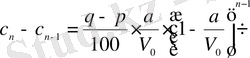Соңғы теңдікті әрбір үшін жазып шығайық:

,
,

.

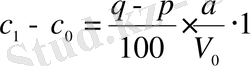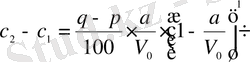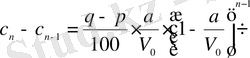Алынған теңдіктерді қоссақ, онда

.

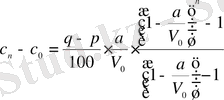Бұдан

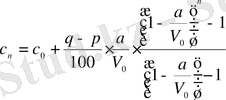
немесе

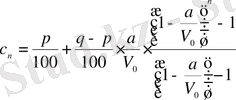
(1.1.12) формула – проценттер теориясындағы күрделі проценттер
заңдылығымен тығыз байланысты.
Күрделі проценттер-орын алады дейміз, егер бір шама кезең-
кезеңімен өзгеріске ұшыраса.
Алдымен, әрбір кезең соңында шама тұрақты 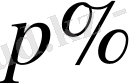өзгерген жағдайды
қарастырайық.
Бастапқы мәні 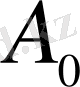тең, 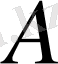шамасы бірінші кезеңнен кейін

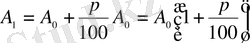
тең болады.
Екінші кезең соңында

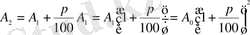
болады. Мұнда - әр кезеңде шамасының неше есе ұлғаятындығын
көрсетеді. Алдыңғы концентрацияға қатысты мысалдарда бұл шама 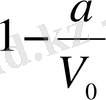тең
болатын.
кезеңнен кейін шамасы

(1.1.13)

формуласымен табылатындығы түсінікті. Бұл формуладан шамасы
геометриялық прогрессиямен өсетіндігін (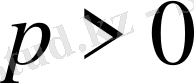) немесе кемитіндігін ()
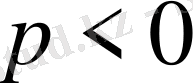байқауға болады.
(1.1.13) формуланы келесі мысал шешу үшін қолданайық.
Мысал 4. Банк жылына үстеме төлейді. Салынған сомма неше жылда екі
есе ұлғаяды?
Шешуі. Салынған сома мөлшерін 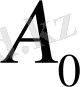теңге деп есептейік. Сонда
жылдан кейін бұл сома 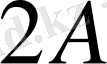теңгеге тең болады. Сондықтан (1.1.13)
формулаға сәйкес

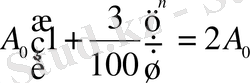
немесе .
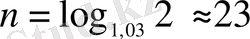Яғни, жауабы 23 жылдан соң.
(1.1.13) формуланың практикада қолдану аясы өте кең. Мысалы келесі жағдайды
қарастырайық.
1) Егер процентті қосу әрбір кезеңде бір рет емес рет орын алсын,
онда

.

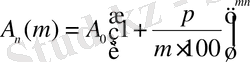2) Егер бірінші кезеңде 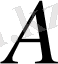шамасы 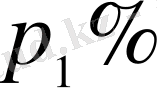өзгерсе, ал екінші кезеңде
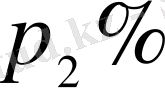өзгерсе және т.с.с. Сонда, егер 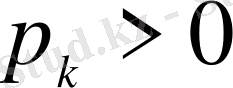болса, онда бұл кезеңде
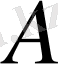шамасы өсетіндігі, ал егер 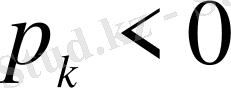болса, онда бұл кезеңде 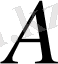шамасы
кемитіндігі белгілі.
Жоғарыда дәлелденгеніндей, әрбір кезеңде 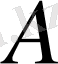шамасының 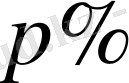- ке
өзгеруі, оны 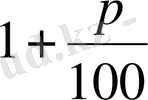көбейткенге тең. Сондықтан, (1.1.13) формуладан

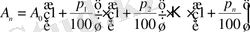. (1.1.14)

Кейбір теңдеулер құруға арналған есептерде орташа проценттік өсім
түсінігі енгізіледі. Бұл терминнің мағынасы келесіде: кезеңдегі
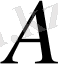шамасынан тұрақты өсім алуды осы кезеңде әртүрлі өсім алу арқылы қол
жеткізілуі, яғни

.

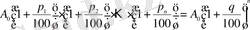Бұл формуланы қолданылуын көрсету үшін, келесі мысалды қарастырайық.
Мысал 5. Өндіріс орнының бірінші жылдағы өнім шығаруы 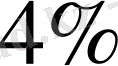ұлғайған.
Келесі жылы ол ұлғайған. Осы 2 жыл арасындағы өндіріс орнының орташа
өсімі қандай?
Шешуі. Орташа өсімді 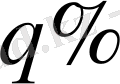деп есептейік, сонда

.

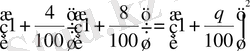Бұдан

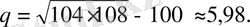
1.2 Қозғалыс - қа арналған есептер.

Бұл параграфта қозғалысқа қатысты есептер қарастырылады. Құрылатын
теңдеулер жүйесі негізінен келесі параметрлерге қатысты құрылады:
• - жүрілген жол;
• - қозғалыстағы дененің жылдамдығы;
• - қозғалысқа кететін уақыт.
Бұл белгілеулер есепті шешкенде қателік жібермеу үшін енгізіліп отыр.
Қозғалыс - қа қатысты есептерді шешкенде келесі болжамдар
орындалады деп есептейміз:
а) белгілі бір жол бөліктерінде қозғалыс бірқалыпты, яғни жүрілген жол

формуласымен анықталады.
б) Қозғалыстағы дененің бұрылуы лездік, яғни дене бұрылған кезде
жылдамдығын жоғалтпайды және бұрылу үшін уақыт кетірмейді.
в) Егер дене өзен ағысымен қозғалса, онда өзен ағысының жылдамдығы мен
дене жылдамдығы қосылады

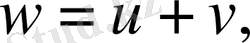
ал егер дене өзен ағысына қарсы қозғалса, онда дене жылдамдығынан өзен
ағысының жылдамдығы алынып тасталады

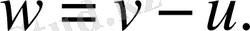
Егер есептің мәтінінде салдың қозғалысы жайында айтылса, онда оның
жылдамдығы өзен ағысының жылдамдығымен тең деген сөз.
Қозғалыс есептеріне қандай да бір жұмысты орындау, су қоймаларын
толтыру немесе босату жұмыстарына қатысты есептер де жатады. Мүндай типтегі
есептерде барлық жұмыс немесе су қоймасының толық көлемі жүрілген жолды, ал
объектілердің өнімділігі жылдамдықты білдіреді.
Қозғалыс - қа қатысты есептерді шешпес бұрын, иллюстративтик сызба
салып алған дұрыс. Бұл сызбада барлық кездесулер, іркілістер және
бұрылыстар айқындалғаны дұрыс. Жақсы келтірілген сызба есептің мәтінін
толық түсінуге мүмкіндік береді.
Мұндай сызбалардың кейбірулері төменде келтірілген:
а) бір-біріне қарсы қозғалыс (сурет 3). Егер бір-біріне 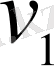және
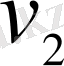жылдамдықтармен қарсы қозғалған екі нүктенің арақашықтығы 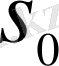болса,
онда олардың кездесу уақыты

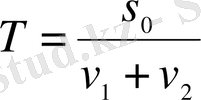
формуласымен анықталады.

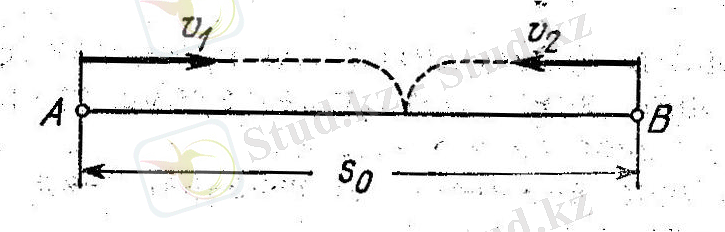
сурет 3

б) бір-бірімен бір бағытта қозғалыс (сурет 4). Егер бір-бірімен бір
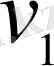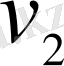бағытта және жылдамдықтарымен қозғалған екі нүктенің
арақашықтығы 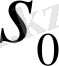болса, онда екінші нүктенің (жылдамдығы 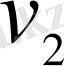) бірінші
нүктені (жылдамдығы 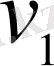) қуып жету уақыты

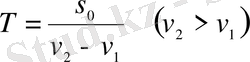
формуласымен анықталады.

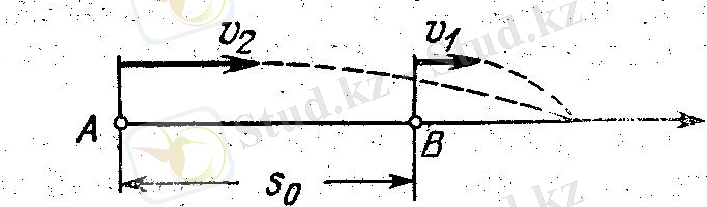
сурет 4

Енді есептің мәтініне қатысты есептерді құруға кірісейік.
Есеп 4. А және В қалалары өзеннің жағасында орналасқан және судың ағысы А
қаласынан В қаласына қарай бағытталған. Сағат таңғы 9-да А қаласынан В
қаласына қарай сал шықты. Тура осы уақытта В қаласынан А қаласына қарай
қайық шығып, ол салмен 5 сағаттан кейін кездескен. А қаласына жеткенен соң,
қайық кері бұрылып, В қаласына сал екеуі бір мезетте жеткен. Қайық пен
сал В қаласына сол күнгі кешкі сағат 9-да жете ала ма?
Шешуі. Бұл есептің шарттарына сай келесі сызбаны саламыз (сурет 5).

сурет 5

Енді есептен теңдеуді құруға мүмкіндік беретін шарттарды бөліп
алайық. Олар екеу:
1. қайық пен сал бір-біріне қарсы бір мезетте шығады және олар 5 сағаттан
кейін кездеседі;
2. қайық В қаласына салмен бірге бір мезетте қайтып жетеді.
Бұл сөйлемдерді жазу үшін, алдымен қандай айнымалыларды енгізу керектігін
шешіп алған дұрыс. Айнымалыларды енгізер кезде, есеп шарттары қарапайым
болатындай етіп енгізген дұрыс және бұл шарттарда ізделінді шаманың
қатыспауы да мүмкін. Мысалы берілген есепте су ағысының (салдың)
жылдамдығын деп, ал қайық жылдамдығын деп белгілеп алған
дұрыс. Ал А және В қалаларының арақашықтығын 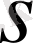арқылы белгілейік
(Ізделінді уақыт болғанымен, ол үшін қосымша айнымалы енгізудің қажеті
жоқ). Сонда

Есептің шарты Теңдеуі

қайық пен сал бір-біріне қарсы бір
мезетте шығады және олар 5 сағаттан
кейін кездеседі;

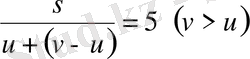
қайық В қаласына салмен бірге бір
мезетте қайтып жетеді.

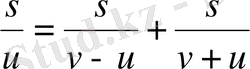
Соңғы қатыстағы сал қозғалысының уақыты, 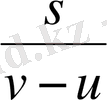- қайыққа ағысқа
қарай жүзгенде кететін уақыты және 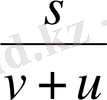- қайықтың ағыспен жүзгенде
кететін уақыты.
Сонымен, үш белгісізі бар екі теңдеулер жүйесін аламыз. Бұл теңдеулер
жүйесінен 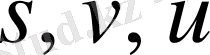шамаларын бірмәнді анықтау мүмкін еместігі белгілі. Енді
есептің шартына қайта оралайық, яғни не табу керек? Есептің шарты бойынша
қайық пен сал В қаласына сол күнгі кешкі сағат 9-да жете ала ма деген
сұрақ, яғни қозғалысты 12 сағатпен салыстыру керек.
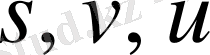Қозғалыс уақыты болғандықтан, айнымалыларын емес,
қатынасын табу керек.
Бөлшек – сызықты функцияның қасиетін пайдаланып, теңдеулер жүйесін
келесі түрде жазуға болады:

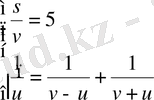
немесе

.

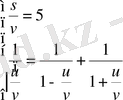Сонда теңдеулер жүйесі 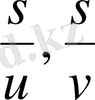екі айнымалыдан ғана тәуелді болады. Екінші
теңдеуден қатынасын табайық. Ол 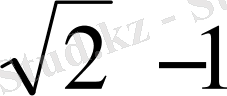тең. Сонымен

, =.

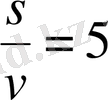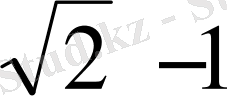Бұл екі қатынасты пайдаланып, қатынасын табамыз, яғни

.

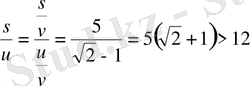Бұдан қайық пен сал сол күнгі кешкі сағат 9-да В қаласына бір мезетте жүзіп
келуі мүмкін емес екендігі шығады.
Тағы бір есеп қарастырайық.
Есеп 4. Екі велосипедші мен жаяу жолаушы бір мезетте А қаласынан В
қаласына қарай шықты. Бір сағаттан аса уақыттан кейін бірінші
велосипедшінің велосипеді бұзылып, ол қалған жолды велосипедпен жүргенге
қарағанда 4,5 есе жай жаяу жүреді. Оны велосипед бұзылғаннан сағаттан
кейін, екінші велосипедші, ал велосипед бұзылғаннан 10,8 сағаттан кейін,
жаяу жүруші озып өтеді. Велосипед бұзылғанға дейін, екінші велосипедші
жаяу жүрушінің велосипед бұзылғанға дейінгі жүрген жолы мен онан кейінгі
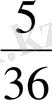сағатта жүрген жолынан екі есе көп жол жүрген. Қозғалыс басталғаннан
кейін, велосипед неше сағаттан кейін бұзылған?
Шешуі. Бұл есептің сызбасы 8 суретте келтірілген. Бұл есеп үшін төрт
айнымалы енгізген дұрыс. 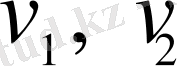- сәйкесінше бірінші және екінші
велосипедшілердің жылдамдығы, - жаяу жүрушінің жылдамдығы және
- велосипед бұзылған уақыт.

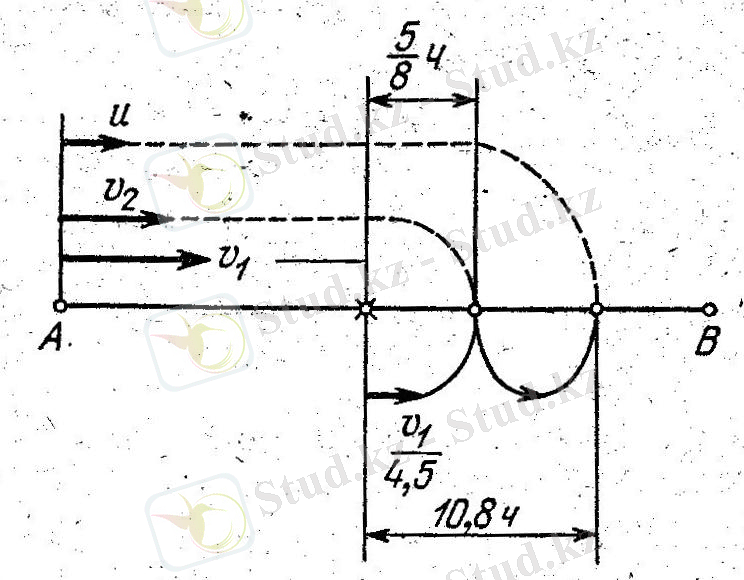
сурет 8

Есептің шарты бойынша 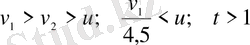болатындығы түсінікті. Есеп мәтінінен
теңдеулерді құруға болатын шарттарды бөліп алайық.

Есептің шарты Теңдеуі

Бірінші велосипедшіні бұзылғаннан
сағаттан кейін екінші
велосипедші озып өтті;

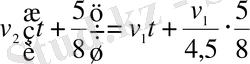
Бірінші велосипедшіні бұзылғаннан
10,8 сағаттан кейін жаяу жүруші озып
өтті;
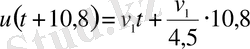
Велосипед бұзылғанға дейін, екінші
велосипедші жаяу жүрушінің
велосипед бұзылғанға дейінгі жүрген
жолы мен онан кейінгі сағатта
жүрген жолынан екі есе көп жол
жүрген

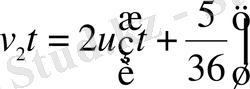
Сонымен құрылған теңдеулер жүйесінде үш теңдеу төрт белгісіз бар. Сондықтан
барлық айнымалыларды табу мүмкін емес. Бірақ құрылған теңдеулер 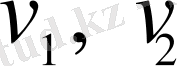және
айнымалыларына қатысты сызықты біртекті екенін ескерген жөн. Егер
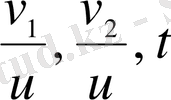теңдеулердің барлығын - ға бөлсек, онда үш белгісізі бар үш
теңдеулер жүйесін аламыз:

.

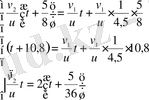Екінші теңдеуден 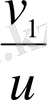тауып, бірінші теңдеуге қойсақ:

.

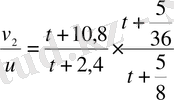Үшінші теңдеуді пайдалансақ, онда

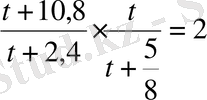
немесе

.

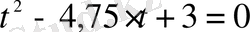Квадрат теңдеуді шеше отырып, келесі мәндерді анықтаймыз:

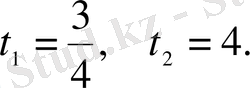
Есептің шарты бойынша, велосипед бір сағаттан кейін бұзылған. Сондықтан
есептің жауабы:
Қозғалыс есептеріне жататын айналмалы жол есептерін қарастырайық.
Есеп 4. Үш жарысқа түсуші жүргізулер бір мезетте айналма жолдың бір
нүктесінен, тұрақты жылдамдықпен жарысқа кірісіп кетті. Бірінші жүргізуші
бесінші айналымын жасап жатқанда екінші жүргізушіні жарысқа кірісу
нүктесіне диаметриальды қарама –қарсы жерде қуып жетті, ал жарты сағаттан
кейін үшінші жүргізушіні екінші рет қуып жетті. Екінші жүргізуші, үшінші
жүргізушіні жарыс басталғаннан кейін, ең алғаш рет, үш сағаттан кейін қуып
жетті. Егер екінші жүргізуші бір айналымды жиырма минуттан кем емес уақытта
жүріп өтсе, онда бірінші жүргізуші бір сағатта неше айналым жасайды?
Шешуі. Мұндай есептің күрделілігі келесіде: Жылдамдығы үлкен жүргізуші
айналма жол бойымен қозғала отырып, бір уақыт мезгілінде жылдамдығы аз
жүргізушінің соңында болуы мүмкін.Сондықтан алдында кетіп бара жатқан
жүргізуші соңында келе жатқан жүргізушіні қуып жету керек болатын жағдай
туындайды.
Дегенмен, есептің шиеленіскендігіне қарамай, есепті шешу кезінде
келесі жайтты ескерген жөн: егер бірінші жүргізуші екінші жүргізушіні қуып
жетсе, ол екінші жүргізушіге қарағанда айналма жолды бір айналым артық
жүріп өтеді.
Есепті шешу үшін келесі айнымалыларды енгізейік. Айналма жол
ұзындығын деп, ал сәйкесінше бірінші,екінші және үшінші
жүргізушілердің жылдамдықтарын - деп белгілейік. Есеп шартынан
болатындығы белгілі.
Бірінші жүргізуші екінші жүргізушіні жылдамдықпен, ал үшінші
жүргізушіні жылдамдықпен қуып жетеді. Екінші жүргізуші үшінші
жүргізушіні жылдамдықпен қуып жетеді.
Жүргізушінің біреуі екіншісін қуып жеткенде, екіншісіне қарағанда
жол артық жүріп өтеді, ал екінші рет қуып жеткенде жол артық
жүреді және т.с.с.
Енді теңдеулерді құруға арналған схеманы келтірейік:

Есептің шарты Теңдеуі

Бірінші жүргізуші бесінші айналымын
жасап жатқанда екінші жүргізушіні
жарысқа кірісу нүктесіне
диаметриальды қарама –қарсы жерде
қуып жетті (4,5 айналымда);

Жарты сағаттан кейін үшінші
жүргізушіні екінші рет қуып жетті;

Екінші жүргізуші, үшінші жүргізушіні
жарыс басталғаннан кейін, ең алғаш
рет, үш сағаттан кейін қуып жетті;
Егер екінші жүргізуші бір айналымды
жиырма минуттан кем емес уақытта
жүріп өтсе;

Мұндағы үшінші шарт, есептің бірмәнді шешімін алу үшін қажет.
Есептің шарты бойынша , айнымалыларын емес,
қатынасын табу керек. Сондықтан, есепті шешу үшін, әрбір жүргізушінің бір
сағатта жасайтын айналым санын жаңа айнымалылары арқылы белгілейік,
сонда:

.

Енді теңдеулер жүйесін келесі түрде жазуға болады:

Бірінші және үшінші теңдеуді қосып, шыққан қосындыдан екінші теңдеуді
шегерсек, онда айнымалысына қатысты келесі квадрат теңдеуді аламыз:

Квадрат теңдеуді шешсек, онда

Бірінші шешім төртінші шартты қанағаттандырмайды, яғни бірінші теңдеуден
болғанда Яғни бірінші жүргізуші бір сағатта үш айналым
жасайды.
Бұл параграфтың соңғы есебі ретінде жұмыс істеуге қатысты есепті
шешейік.
Есеп 5. Туннель қазушы екі машина бір-біріне қарсы жүре отырып, жұмысты 60
күнде бітірді. Егер бірінші машина 18 күн, ал екіншісі 16 күн жұмыс
істегенде, олар туннелдің 60 метрін жүруші еді. Егер бірінші машина екінші
машинаның барлық жұмысының бөлігін, ал екінші машина бірінші
машинаның 0,3 жұмысын істесе, онда бірінші машинаға екінші машинаға
қарағанда 6 күн қажет болар еді. Әрбір машина күніне неше метр туннель
қазады?
Шешуі. Қозғалысқа қатысты есептерге ұқсас, мұнда да әрбір машинаның
өнімділігін сәйкесінше (метркүніне) және (метркүніне) деп
белгілейік. Сонда туннельдің ұзындығы

анықталады. Мұнда - бірінші машинаның орындаған жұмыс көлемі, ал
- екінші машинаның орындаған жұмыс көлемі.
Есепке қатысты теңдеулерді құрайық.

Есептің шарты Теңдеуі

Егер бірінші машина 18 күн, ал
екіншісі 16 күн жұмыс істегенде,
олар туннелдің 60 метрін жүруші еді;

Егер бірінші машина екінші машинаның
барлық жұмысының бөлігін, ал
екінші машина бірінші машинаның 0,3
жұмысын істесе, онда бірінші
машинаға екінші машинаға қарағанда 6
күн қажет болар еді;

Кейбір ықшамдаулардан кейін, теңдеулер жүйесі келесі түрге келтіріледі:

.

Екінші теңдеуді бөлсек, онда

Квадрат теңдеуді шешсек:

немесе .

Табылған мәнді бірінші теңдеуге қойсақ, онда

мкүніне, мкүніне.

3. Айнымалылылар саны теңдеулер санынан
көп болатын есептер.

Өткен параграфта біз айнымалылар саны теңдеулер санынан көп болатын
есептерді көрген болатынбыз. Мұндай есептердің пайда болуы, негізінен
есептің шартына байланысты болады. Мысалы, егер анымалыларды теңдеуді
құруға ыңғайлы етіп енгізсек, онда ізделінді айнымалы теңдеулерде
кездеспеуі мүмкін. Бірақ ол енгізілген айнымалылардың комбинациясы болуы
мүмкін. Сондықтан теңдеулер жүйесіндегі барлық айнымалыларды бірмәнді
анықтау мүмкін емес. Дегенмен, ізделінді комбинация бірмәнді анықталуы
мүмкін.
Осындай кластарға жататын есептерді қарастырайық.
Есеп 5. Оқушы сөмке, қалам және кітап сатып алу үшін, белгілі бір сома
жұмсады. Егер сөмке 5 есе, қалам 2 есе, ал кітап 2,5 есе арзан болғанда,
онда оқушы небары 8 теңге жұмсайтын еді. Егер сөмке 2 есе, қалам 4 есе, ал
кітап 3 есе арзан болғанда, онда оқушы 12 теңге жұмсайтын еді. Негізінде,
барлық жұмсалған сома неше теңге және сөмке мен қаламның қайсысына көп сома
төленді?
Шешуі. Теңдеу құру үшін, үш айнымалы енгізу жеткілікті, яғни -
арқылы сөмкеге, - арқылы қаламға және - арқылы кітапқа
жұмсалған соманы белгілеп алайық. Сонда теңдеулер жүйесін келесі түрде
жазуға болады:

немесе

Сонымен, біз үш айнымалысы бар екі теңделер жүйесін алдық. Бұл теңдеулер
жүйесінен , және мәндерін бірмәнді анықтауға
болмайтындығы түсінікті. Бірақ есептің шарты бойынша оларды анықтаудың
қажеті жоқ, яғни есептің шарты бойынша олардың сомасын табу жеткілікті.
Сондықтан екі теңдеуді бір-біріне қосып шығайық, сонда

,

Бұдан

Сонымен, барлық жұмсалған сома 28 теңге. Енді және
айнымалыларын салыстыру қажет. Ол үшін теңдеулер жүйесінен
айнымалысын жояйық, яғни екінші теңдеуден бірінші теңдеуді алып тастайық.
Сонда

немесе

, , және екенін ескерсек, онда екендігі
шығады. Онда соңғы теңдіктен екендігі шыгады, яғни Сонымен,
сөмке қаламнан қымбат екендігі шығады.
Осы типтес тағы бір есепті қарастырайық.
Есеп 5. Құрамында мыс пен қорғасын бар екі қортпа бар. Егер бірінші және
екінші қортпадан 1 кг-нан алсақ, онда шығатын жаңа қорпадағы мыс мөлшері
. Егер жалпы салмағы 7 кг болатын, I бөлік бірінші қорпадан және II
бөлік бірінші және екінші қорпадан алсақ, онда жаңа қорпадағы мыс мөлшері
болғаны белгілі. Егер II бөлік бірінші қорпадан және I бөлік екінші
қорпадан алсақ, онда жаңа қорпадағы мыс салмағы анықтаңыз.
Шешуі. Қорпалардағы мыстың проценттік мөлшерін келесі түрде белгілеп
алайық: - I бөліктегі - II бөліктегі. I бөліктің салмағын
, ал II бөліктің салмағын деп белгілеп алайық. Сонда есепке
қатысты теңдеулерді келесі түрде құруға болады.

Есептің шарты Теңдеуі

Егер бірінші және екінші қортпадан 1
кг-нан алсақ, онда шығатын жаңа
қорпадағы мыс мөлшері ;

жалпы салмағы 7 кг болатын, I бөлік
бірінші қорпадан және II бөлік
бірінші және екінші қорпадан алсақ;

I бөлік бірінші қорпадан және II
бөлік бірінші және екінші қорпадан
алсақ, онда жаңа қорпадағы мыс
мөлшері болғаны белгілі.

Сонымен, төрт айнымалысы бар үш теңдеулер жүйесін аламыз:

Бұл есепте де барлық айнымалыларды бірмәнді анықтауға болмайтындығы
түсінікті. Сондықтан есептің шартында не табу керек екендігін қарастырайық,
яғни есептің шарты бойынша II бөлік бірінші қорпадан және I бөлік екінші
қорпадан алғанда, шығатын қортпадағы мыс салмағын анықтау қажет:

.

Сонымен, есептің шешімін анықтау үшін, табу жеткілікті. Ол
үшін, бірінші және екінші теңдеуді көбейтіп, шыққан көбейтіндіден үшінші
теңдеуді алайық:

.
Сонда
кг.
Есеп 5. Су қоймасы бес құбыр ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.