Жұп және тақ, периодтық және элементарлық функциялардың анықтамасы мен классификациясы


ЖҰП ЖӘНЕ ТАҚ ФУНКЦИЯЛАР
Анықтама. Егер М жиынының құрамына кез келген х санымен бірге оған симметриялық - х саны да кірсе, ол М жиыны симметриялық жиын деп аталады.
Симметриялық жиындарға мысалдар: барлық бүтін сандар жиыны, [-5, +5] сегментіндегі барлық сандардың жиыны, (-b, +b) интервалындағы барлық сандардың жиыны.
Анықтама. Егер f(х) симметриялық облыста берілсе және сол облыстағы аргумент x-тін, кез келген мәні үшін
f(-x) =f(x) (1)
теңдігі орындалса, f (х) сол симметриялық облыста жұп функция деп аталады.
Басқаша айтқанда: егер аргументтің мәні х-ті -х - ке ауыстырғанда f(x) -тің мәні өзгермейтін болса, f( х) -ті жұп функция деп атайды.
М ы с а л ы: у = sес x;
у = х
2n
(бұндағы
n
- натурал сан),
у = 2х
4
- 5х
2
-
3;
у = 2 -
sіn
2
х;
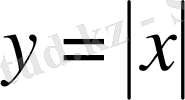 функциялары
функциялары
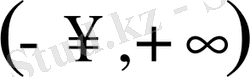 интервалында жүп функциялар.
интервалында жүп функциялар.
Енді f (х) = ln(1- х) + ln (1 +х) функциясы өзінің анықталу облысында жұп функция екенін көрсетелік.
Шынында, берілген f (х) функциясы (-1, +1) интервалында анықталған.
F(-x) =ln[1-(-x) ] +ln[1+(-x) ] =ln(1+x) +ln(1-x) =f(x) .
Демек, f (-х) =f(х) болады, яғни берілген функция (-1, + 1) интервалында жұп функция.
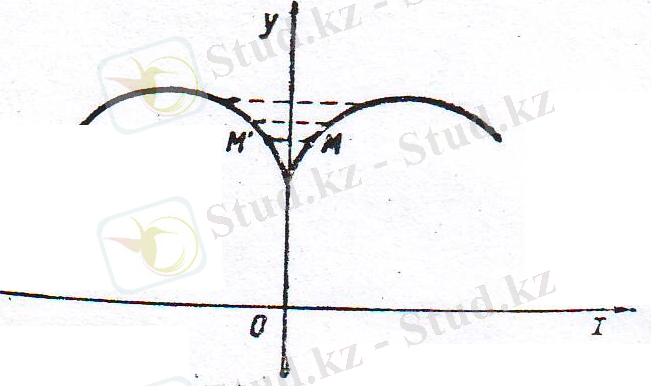
Жұп функцияның графигі ординаталар осіне симметриялық түрде орналасатындығын f( -х) =f(х) теңдігінен көруге болады.
Анықтама. Егер f( х) симметриялық облыста беріліп, облыстағы аргумент x-тің кез келген мәні үшін
f (-х) = - f(х) . (2)
теңдігі орындалса, яғни аргументтің таңбасы кері таңбаға ауысқанда функцияның да таңбасы кері таңбаға ауысса, f(x) сол облыста тақ функция деп аталады.
М ы с а л ы: у=х 3 ; у=7х 5 - 2х 3 + х; у=сosес х; у=х 2n-1
(бұндағы n -натурал сан) ; y=
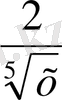 Equation. 3 ; у=
х
x ;
у = сtgх
функциялары тақ функциялар.
Equation. 3 ; у=
х
x ;
у = сtgх
функциялары тақ функциялар.
Енді g
(х)
=ln
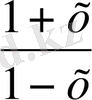 Equation. 3 өзінің анықталу облысында тақ функция екенін көрсетелік.
Equation. 3 өзінің анықталу облысында тақ функция екенін көрсетелік.
Шынында: бұл функцияның анықталу облысы (-1, + 1) интервалы. Ал
g(-x) =ln
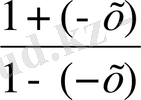 Equation. 3 =ln
Equation. 3 =ln
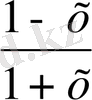 Equation. 3 =ln(1-x) -ln(1+x) =
Equation. 3 =ln(1-x) -ln(1+x) =
=- [ln(1+x) -ln(1-x) ] =-ln
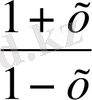 Equation. 3 =-g(x),
Equation. 3 =-g(x),
яғни g (-х) = -g(х) . Демек, берілген функция g(x) (-1, +1) интервалында тақ функция болады. Тақ функцияның графигі координаталар системасының бас нүктесіне симметриялық түрде орналасады.

Сөйтіп, егер тақ функция х=0 нүктесінде анықталған болса, функцияның ол нүктедегі мәні нольге тең. Бұдан х = 0 нүктесінде анықталған тақ функцияның графигі міндетті түрде координаталар системасының бас нүктесі арқылы өтетіндігіне көзіміз жетеді.
Периодты функциялар
Анықтама. Егер f(х) функциясының анықталу облысындағы аргумент х-тің әрбір мәні үшін f(x+L) =f(x) (1)
теңдігі орындалатын нольге тең емес L саны табылатын болса, f(х) - периодты функция, L саны - f(х) -тің периоды деп аталады.
Егер (1) теңдікті х + l нүктесі үшін қолдансақ,
f[( х+l) +l] =f(x+l) =f(x), немесе
f(x+2l) =f(x)
болар еді. Бұл процесті соза берсек, мына теңдіктер орындалар еді:
F(х+3l) =f(х) .
f(х+4l) =f(х),
F(х+nl) =fх)
. .,
Сонымен, егер периодты f(
х)
функциясының анықталу облысында
х
болса,
х + nl
сандары да
(n
- кез келген натурал сан) f(х) -тің анықталу облысында болады және
nl
сандары f(x) -тің периодтары болады. Периоды L-ге тең функция
f(х)
үшін
f(х) =f[(х-I) +l]
теңдігі де орындалатын болғандықтан, ( -L) саны да
f(х) -тің
периоды болады. Сондай-ақ жоғарыдағыша байымдап тек
 саны ғана емес, -
2l, -3l,
. . . ,
-nl
сандарының да
f(х)
үшін периодтар болатындығын байқау қиын емес.
саны ғана емес, -
2l, -3l,
. . . ,
-nl
сандарының да
f(х)
үшін периодтар болатындығын байқау қиын емес.
Сөйтіп, егер
f(х)
-периодты функция болып, оның периоды
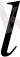 болса, k
l
(бұндағы k
-
кез келген нольге тең емес бүтін сан,
k=±1, ±2\
. . . ;
±nl)
сандары да f(x) -тің периодтары болатыны айқындалады.
болса, k
l
(бұндағы k
-
кез келген нольге тең емес бүтін сан,
k=±1, ±2\
. . . ;
±nl)
сандары да f(x) -тің периодтары болатыны айқындалады.
Демек, егер
f(х) (-
 , +
, +
 ) интервалында периодты функция болса, ол функцияның міндетті түрде оң периоды болуға тиіс, өйткені
) интервалында периодты функция болса, ол функцияның міндетті түрде оң периоды болуға тиіс, өйткені
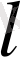 және
және
 сандарының бірі оң сан болатыны анық. Сондықтан да (-
сандарының бірі оң сан болатыны анық. Сондықтан да (-
 , +
, +
 ) интервалындағы периодты функцияның оң периодтары сансыз көп. Оң периодтарының жиынында ең кіші
ω
саны болуы мүмкін. Бұл санды ең кіші период немесе негізгі период деп атаймыз.
) интервалындағы периодты функцияның оң периодтары сансыз көп. Оң периодтарының жиынында ең кіші
ω
саны болуы мүмкін. Бұл санды ең кіші период немесе негізгі период деп атаймыз.
Периодты функцияларға мысалдар келтірейік.
1) Тригонометриялық функциялар:
sinx, cosx, tgx, ctgx.
sinx пен соsx-тің ең кіші (немесе негізгі) периоды 2π, ал tgx пен сtgх-тің периоды π .
2) f
(х) =х-Е (х)
функциясы (-
 , +
, +
 ) интервалында - периодты функция және оның негізгі периоды 1.
) интервалында - периодты функция және оның негізгі периоды 1.
Ш ы н ы н д а:
f(x+1) ) =x+1-E(x+1) =x+1-[E(x) +
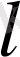 ] = x-E(x) =f(x),
яғни
] = x-E(x) =f(x),
яғни
f(x+1) =f(x) .
Элементар функциялар. Кері функция. Күрделі функция.
Параметрлі түрде берілген функция.
Бір аргументті функциялардың ішінде элементарлық функциялар деп аталатындары әдейі бір топқа бөлінеді. Олардын, бұлай аталуының себебі: олар басқа элементарлық емес функциялардан тарихта бұрын шықкан, жан-жакты зерттелген, кұрылысы біркелкі қарапайым болып келеді, және жиі колданылады.
Элементарлык. емес функцияларды көбінесе арнаулы ф у н к ц и я л а р деп атап жүр. Бұл функциялар математика ғылымының дамуындағы соңғы дәуірлерде кұбылыстардың математикалық жактарын зерттеу мәселелері элементарлық функциялардың мүмкіншіліктері шеңберіне симаумен байланысты пайда болды.
Элементарлык функцияларға төмендегі функциялар жатады:
- Дәрежелікфункцияf (х) =ха(бұндағыа- кез келгеннақты сан) ;
- Көрсеткіштікфункцияф(х) =ах(бұнда а>0) ;
- Логарифмдікфункцияф(х) =lgах(бұнда а>0) ;
- sіnx:, соsх, tgх, сіgх, sесх, соsесх;
5. Кері тригонометриялық функциялар агсsіпх, агссоsх,
агссtgx, агсsесх, агссоsесx
Ескерте кететін бір нәрсе мынау: элементарлық функцияларға алты алгебралық амалды (қосу, азайту, көбейту, бө-лу, бутін оң дәрежеге шуғару және түбірлеу) қолдану.
Барлық элементарлық функцияларды екі типке бөлуге болады:
- Алгебр алық функциялар.
- Трансценденттік функциялар.
Элементарлық алгебралық функциялар мынадай кластарға бөлінеді:
- Рационалдық функциялар.
а) Бүтін рационалдық функциялар.
б) Бөлшек рационалдық функциялар.
2. Иррационалдық функциялар.
Анықтама
. Егер
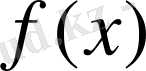 функциясы дәреже көрсеткіші терім емес бүтін сан болатын және коэффициенттері нақты сандар ғана болып келетін айнымалы
функциясы дәреже көрсеткіші терім емес бүтін сан болатын және коэффициенттері нақты сандар ғана болып келетін айнымалы
 тің дәрежелерінің қосындысы
тің дәрежелерінің қосындысы
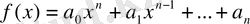 түріне келтірілетін болса,
түріне келтірілетін болса,
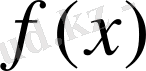 - бүтін рационалдық функция деп аталады.
- бүтін рационалдық функция деп аталады.
Анықтама
. Егер
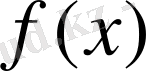 функциясыекі бүтін рационалдық функцияның қатынасы түріне келтірілетін болса, ол бөлшек рационалдық деп аталады.
функциясыекі бүтін рационалдық функцияның қатынасы түріне келтірілетін болса, ол бөлшек рационалдық деп аталады.
Демек, бөлшек рационалдық функцияның жалпы түрі мынадай болатын болды:
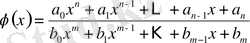
Бұдан
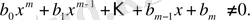
Бөлшек рационалдық функцияларға мысалдар:
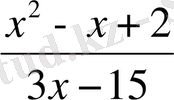 ,
,
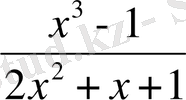 .
.
Егер рационалдық функцияларға түбірлеу амалын колдансақ, иррационалдық функция пайда болады; оған мын а төмендегі мысалдарды келтіре кетейік:
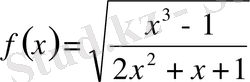 ,
,
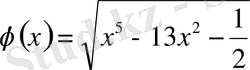 ,
,

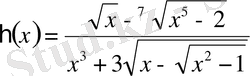
Анықтама. Егер у=f (х) функциясы

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz