Математика пәнінен оқу құралы

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 108 бет
Таңдаулыға:

Лекция 2.

Жиын ұғымы, элементі.

Жиындардың берілу тәсілдері.

Жиындарға қолданылатын амалдар және олардың заңдары.

Лекция мақсаты:

1. Жиын ұғымымен және олардың берілу тәсілдерімен таныстыру.

2. Жиындарға қолданылатын амалдарды және заңдарды есеп шығаруда қолдануға үйрету.

Қазіргі математика салалары мен оның практикада қолданылуын түгелдей дерлік жиындар теориясына негізделген. Өйткені жиындар теориясының ұғымдары математикалық обьектілердің ең жалпы қасиеттерін бейнелейді. Жиындар - математикада негізгі және алғашқы ұғымдардың бірі саналады. Сондықтан да болар, мектеп математикасының негізгі мазмұны болып табылатын “сан”, “теңдеу” және “теңсіздік”, “функция”, т. с. с. ұғымдарды, сондай-ақ сандарға операциялар жүргізу, теңдеулер мен теңсіздіктерді шешуді оқып-үйрету теориялық жиындық ұғымдарды қолдануды көздейді.

“Жиын” қатал анықтама беруге болмайтын, тек қана қарапайым мысалдар арқылы түсіндірілетін, математика ғылымындағы ең жалпы, негізгі ұғым. Математикада, кез келген объектілердің (нәрселер, заттар, әріптер, цифрлар _} планеталар, ұғымдар, фигуралар, сандар, сөздер, адамдар, жануарлар, т. с. с. ) жиынтығы -жиынның мысалы бола алады. Әдетте жиын қанда:й болса да бір белгісі бойынша біріктірілген әртүрлі объектілерден құралады.

Жиындар теориясының негізін салуіпы неміс математигі Георг Кантордың (1845-1918) сөзімен айтқанда: “Жиын дегеніміз өзіміздің ойымызда тұтас бір бүтін больш түсінілетін көптік”.

Ал, “көптік”, “жиын”, “жинақ”, “жиынтық” деген сөздерді тілдік тура мағынасы-алынып отырған объектілер бірнешеу деген ой тудырады. Бұдан әрбір жиыңда міндетті түрде көп (кемінде екі) элемент болу қажет деген жаңсақ пікір тууы мүмкін. Алайда математикада жиынды құрайтын элементтердің санына байланысты, тек бір ғана элементі болатын жиынды немесе элементтері бірнешеу, яғни элементтерінің саны шектеулі (шектелген жиын) жиынды, бірде-бір элементі болмайтын жиынды (шексіз жиын), элементтерінің саны шексіз көп жиынды шексіз жиын деп атайды. Шексіз жиындарды тізіммен беру мүмкін емес.

Жиындарды бір-бірінен айыру үшін оларды латын алфавитінің бас әріптерімен - А, В, С, В, Е, Ғ, . . . , ал элементтерін кіші a, b, c, d, e, . . . әріптермен, сондай-ақ жиындар символикасында бос жиын ∅ таңбасымен белгіленеді, тиісті деген сөздің орнына ∈ таңбасы, “тиісті емес” деген сөздің орнына ∉ таңбасы пайдаланылады.

Шексіз жиындарды фигуралы жақша арқылы көп нүктені пайдаланып белгілеуге болады.

Жиын өзінің элементтері арқылы анықталады, яғни егер кез келген объект жөнінде ол осы жиынға тиісті немесе тиісті емес екендігін айта алатын болсақ, онда жиын берілген деп саналады.

Жиынның берілу тәсілдері:

1) Жиынның барлық элементтерін тізіп көрсету арқылы беріледі.

Мысалы, А жиыны 3, 4, 5, 6 элементтерінен тұрса, онда элементтерін фигуралы жақшаға алып А={3, 4, 5, 6} түрінде жазып, оны "А жиыны 3, 4, 5, 6 элементтерінен тұрады" деп оқиды.

2) Жиынның берілуінің тағы бір төсілі оны құрайтын элементтерінің ортақ қасиетін атау болып табылады. Мұндай қасиетті сипаттамалық қасиет деп атайды.

Мысалға 6 санынан кем натурал сандардың А жиынын қарастырайық. Бұл жерде А жиынының барлық элементтерінің ортақ қасиеті, атап айтқанда, оларды "натурал және 6-дан кіші сан болуы" аталып отыр. Қарастырып отырған А жиынының элементтерін атап шығу қиындыққа түспейді.

А={хх∈N, х<6}. А={ 1, 2, 3, 4, 5}.

Жиынды элементтерінің сипаттамалық қасиеті арқылы беру геометрияда жиі қолданылады. Белгілі бір сипаттамалық қасиеті бар нүктелердің жиынын нүктелердің геометриялық орны дейді.

Анықтама: Егер В жиынының әрбір элементі А жиынының да элементі болса, онда В жиыны А жиынының ішкі жиыны деп аталады.

Анықтама: Егер А жиынының әрбір элементі В жиынының да элементі болса және керісінше, В жиынының әрбір элементі А жиынының да элементі болса, онда А мен В жиындары тең деп аталады да былай жазылады: А=В.

Бұл анықтаманы былай да айтуға болады: егер А⊂В және В⊂А болса, онда А мен В жиындары тең деп аталады.

Көрнекілік үшін жиындарды дөңгелек не сопақша фигуралармен бейнелейді. Оның ішінде сол жиынның элементтері ғана орналасады. Ол дөңгелектерді Эйлер дөңгелектері немесе Эйлер-Венн диаграммалары деп атайды.

(Леонард Эйлер (1707-1783) -Петербург ғылым академиясының мүшесі, Швейцарияда туылған, ал 1727 жылы петербург ғылым академиясының шақыруымен Ресейге келген және мұнда ірі математик дәрежесіне дейін көтерілген. Джон Венн (1886-1921) ағылшын математигі) .

Эйлер-Венн диаграммаларында жиынды тіктөртбұрыш түрінде, ал ішкі

жиынды шеңбер немесе тұйықталған қисық сызықпен кескіндеп көрсетеді.

Екі және одан көп жиындардың элементтерінен тұратын жаңа жиын құруға болады. Бұл жаңа жиын берілген жиындарға қандай да бір амал қолдану нәтижесінде пайда болады.

Анықтама. А және В жиындарынының қиылысуы деп А және В жиындарының екеуіне де тиісті элементтерден және тек қана сол элементтерден тұратын жиынды айтады.

Ажәне В жиындарының қиылысуы былай белгіленеді: С=А∩В.

А∩В={хх∈А жөне х∈В}

А, В жиындарының қиылысуын Эйлер деңгелектері арқылы бейнелесек, екі жиынның қиылысуын боялған аймақ арқылы көрсетуге болады.

Егер А жөне В жиындарының ортақ элементтері болмаса, онда олардың қиылысуы бос жиын болады және былай жазылады:

А∩В=∅.

Бұл жағдайда Ажәне В жиындары қиылыспайды деп айтады. Мысалы, дауысты дыбыстар мен дауыссыз дыбыстар жиындары қиылыспайды, өйткені бұл екі жиынның ортақ элементтері жоқ.

Анықтама. А және В жиындарының бірігуі деп не А не В жиындарының ең болмағанда біреуіне тиісті элементтерден және тек қана сол элементтерден тұратын жиынды айтады.

А∪В={х/ х∈А немесе х∈В}

А және В жиындарының бірігуін А∪В деп белгілейді, мұндағы ∪ жиындардың бірігуінің белгісі. Егер А жөне В жиындары элементтерінің сипаттамалық қасиеттері көрсетілген болса, онда А∪В жиынына осы қасиеттердің ең болмағанда біреуіне ие болатын элементтер енеді.

Мысалға, А-сыныптағы математика үйірмесіне қатысатын оқушылардың жиыны, ал В-сол сыныптағы физика үйірмесіне қатысатын оқушылар жиыны болсын.

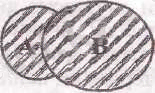
Сонда А жиыны элементтерінің сипаттамалық қасиеті -“математика үйірмесіне қатысуы”, ал В жиыны элементтерінің сипаттамалық қасиеті - “физика үйірмесіне қатысуы” болып табылады. Сонда берілген жиындардың бірігуіне аталған үйірмелердің ең болмағанда біреуіне қатысатын оқушылар енеді. Бұл оқушылардың ішінде тек математика үйірмесіне немесе екі үйірменің екеуіне де қатысатын оқушылар болуы мүмкін.

А∩В=∅ деп санап, А жөне В жиындарын Эйлер-Венн диаграммалары арқылы кескіндесек, онда суреттегі штрихталған бүкіл бөлік А∪В жиынын көрсетеді.

Егер В⊂А болса, онда А жиынның В жиынына тиісті емес элементтерінің жиыны В жиынының А жиынындагы толықтауышы деп аталады және В _А арқылы белгіленеді .

А және В жиындарының айырмасы деп А жиынына тиісті және В жиынына тиісті емес элементтер жиынын айтады . А және В жиындарының айырмасын А\В символы арқылы белгіленеді.

А\В={х/х∈А және х∉В}

Мысалы, егер А={а, Ь, с, d, е}, В={d, е, к, 1} болса, онда А\В ={а, Ь, с} болады. А және В жиындарын Эйлер -Венн диаграммалары көмегімен кескіндесек _э онда А\В жиыны боялған бөлік болады.

Лекция 3. Графтар.

Графтардың түрлері.

Жазық граф туралы Эйлер теоремасы.

Лекция мақсаты:

1. Граф ұғымы және түрлерімен таныстыру.

2. Жазық граф туралы Эйлер теоремасын есеп шығаруда қолдана алу.

Математикада әртүрлі обьектілер арасында (сан, шама, фигура) және олардың қасиеттерінің арасында да баййланыстар зерттеледі. Мысалы, сандар арасында: тең, кем, артық, 1-і артық, 2 есе кем, кейін, бұрын, арасында, соңында т. с. с. қатыстары қарастырылады. Натурал сан ұғымын қалыптастыру -бастауыш математика курсының негізгі ұғымы және жалпы математика сандар арасындағы әртүрлі өзара байланысты зерттей отырып дамиды. Ал геометрияда түзулер арасында тең, параллель, перпендикуляр, фигуралар арасында тең, ұқсас; жиыңдар арасында бірігу, қиылысу, ішкі жиын, тең жиын, т. б. қарастырылады.

Екі жиын арасындағы қатысты бинарлық қатыс деп атайды.

Анықтама. X жиынының элементтерінің арасындағы немесе Х жиынындағы қатыс деп ХхХ декарттық көбейтіндісінің кез келген ішкі жиынын атайды.

Қатысты латынның бас өріптерімен белгілейді: P, Q, R, S, . . . т. с. с. Сонымен, егер Х жиынының элементтерінің арасындағы қатыс R болса, онда R⊂ХхХ болады.

Қатыстың кескінін, яғни сызбаны граф дел атайды.

Граф, график - гректің сөзі, "жазамын" деген мағынасын білдіреді.

Х жиынында берілген R қатысы X жиынынан алынған осы қатыспен байланысқан элементтердің реттелген қостарын тізіп жазу арқылы беріледі. Бұл жағдайда қатыстың элементтерін тізіп жазу формасы әртүрлі болуы мүмкін. Мысалы, Х = {4, 5, 6, 7, 9} жиынындағы қандай да бір R қатысының берілуін мынандай қостар жиыны {(5, 4), (6, 4), (6, 5), (7, 4), (7, 5), (7, 6), (9, 4), (9, 5), (9, 6), (9, 7) } немесе сызбадағы граф арқылы беруге болады.

Көп жагдайда X жиынындағы R қатысы осы қатыста болатын элементтер қостарының жиынының сипаттамалык қасиетін көрсетү арқылы беріледі. Бұл қасиет екі айнымалысы бар сөйлем. Яғни теңдеу және теңсіздік түрінде тұжырымдалады. Мысалы, N натурал сандар жиынындағы мына қатыстар: “х саны у-тен артық”, “х саны у-тен 3 есе кем” т. с. с.

Х⊥У, ХУ, х=у+1, у=3+х, х>у, т. с. с.

Х={1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 15}, х=3у

Орта және бастауыш мектеп математикасында қатыс ұғымы жалпы түрде енгізілмейді, бірақ әртүрлі объекьілер арасындағы нақты қатыстар қарастырылады.

Бастауыш мектеп математикасында сандар арасындағы қатыстарға ерекше көңіл бөлінеді. Оларды қысқа түрде жазылған екі айнымалысы бар сөйлем ретінде, кесте толтыру арқылы т. с. с. түрде беріледі. Қатыстардың көп түрімен бастауыш мектеп оқушылары мазмұнды есептер (мәтіндік) шығаруда кездеседі. Мысалы, “Бір сөредегі кітап саны екінші сөредегіге қарағанда 3 есе артық. Бір сөреден 8 кітапты алып, екінші сөреге 5 кітапты қойғанда екінші сөредегі кітап біріншіге қарағанда 17-ге кем болады. Әрбір сөреде қанша кітап болды?”. Бұл есепті шығарғанда оқушы “есе артық”, “кем” қатыстарын жақсы білуі керек.

Математикада екі объектінің арасында әртүрлі қатыстар қандай да бір Х жиынында қарастырылып, қостардың жиынын береді. Қатыстың қасиеттеріне қарай оларды ортақ қасиеттері бойынша классификациялау керек.

Рефлексивтілік. Егер әрбір элемент өзімен өзі R қатыста бола алса, онда R қатысы рефлексивті деп аталады.

Бұл анқытаманы қысқаша былай жазуға болады.

R рефлексивті: ⇔∀х⊂Х, х Rх

Симметриялық. Егер X жиынындағы х элемент у элементімен R

қатыста және у элементі х элементімен R қатыста болса, онда R қатысы симметриялық деп аталады, яғнм R симметриялық қатыс ⇔∀х, у∈Х үшін хRу⇒уRх.

Антисимметриялық. Егер X жиынын ешбір х және у элементі үшін бір

мезгілде ⇔х≠у, хКу=>уКх бола алмаса, онда R қатысы антисимметриялы деп аталады. Мысалы, “еселі”, "кем" қатыстары 2<5=>5<2

Транзитивтілік. Егер ∀ х, у, z∈Х элементі үшін хRу ∧ уRz=>хRz шығатын болса, онда R қатысы транзитивті деп аталады. "kем" - 3<4 және 4<5=>3<5 “еселі” 8:4 және 4:2⇒8:2

Анықтама. X жиынындағы R қатысты эквиваленттік қатыс деп атайды, егер ол: рефлексивтік, симметриялық, транзитивтік үш қасиетке ие болса.

Анықтама . Егер R қатысы X жиыны қиылыспайтын ішкі жиындарға бөлсе, онда R қатысын эквивалентті қатыс деп атайды.

Анықтама. Егер R қатысы эквивалентті қатыс болса, онда ол X жиынын қиылыспайтын ішкі жиындарға бөледі дейді

Анықтама. Егер X жиынындағы R қатысы антисимметриялық және транзитивтік қасиетке ие болса, онда ондай қатысты реттік қатыс деп атайды.

R қатысы берілген жиынды реттелген жиын деп атайды.

Егер реттік қатыста рефлексивтік қасиет орындалса, онда ол қатаң емес реттік қатыс деп аталады. Ал егер орындалмаса қатаң реттік қатыс деп атайды,

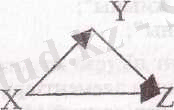
Мысалы: Х-кесінділер жиыны, онда мынадай қатыстар берілген болсын: “тең”, “ұзын”, “параллель”, “перпендикуляр”, графын сыз, қасиетін анықта.

Лекция 4.

Сәйкестік графы мен графигі.

Бейнелеулер және олардың түрлері.

Тең қуаттас жиындар.

Лекция мақсаты:

1. Сәйкестік ұғымын түсіндіру.

2. Бейнелеулер мен олардың түрлерімен таныстыру.

Екі жиынның элементтерінін арасындағы қандай да бір байланыс жиі қарастырылады. Осындай байланысты сәйкестік деп атайды. Мысалы, кесінділердің ұзындығын өлшегенде кесінді мен нақты сандардың арасында, жазыктықтағы нүктелер мен накты сандар қосындысының арасында сәйкестік бар.

А н ы қ т а м а: X және У жиындарының элементтерінің арасындағы сәйкестік деп олардың декарттық көбейтіндісінің ішкі жныны болатын қостардың жиынын айтады.

Ақырлы жиындардың арасындағы сәйкестікті график аркылы көрнекті түрде бейнелеуге болады: Мысалы, Х={3, 5, 7, 9}, У={4, 6} жиындарының арасыңдағы “артық” (үлкен) деген сәйкестікті график арқылы көрсетейік. Ол үшін берілген жиындардың элементтерін нүктелер арқылы кескіндеп, X жиынының элементін кескіндейтін нүктеден У жиыны элементтін кескіндейтін нүктені стрелкамен қосамыз, сонда злементтердің арасында "артық" сәйкестігі орындалуы керек. 5>4 болғандықтан стрелка 5-тен 4-ке қарай; 7>4, 7>6 болғандыктан 7-ден 4-ке, 7-ден 6-ға қарай т. с. с. бағытталады.

X, У сандық жиындардың арасындағы сәйкестікті координаттық жазықтыктағы график арқылы да көрсетуге болады. Ол үшін қандай да бір к сәйкестікте болатын сандардың қосын координаттық жазықтықтағы нүкгелер аркылы бейнелейді. Сонда алынған фигура R сәйкестігінің графигі болады.

Берілген сәйкестікте болатын сандардың қосын жазайык: (5, 4), (7, 4), (7, 6), (9, 4), (9, 6) . X жиынының элементтерін ОХ осінің бойынан, ал У жиынының элементтерін ОУ осінің бойынан алып, көрсетілген сандардың қосына сәйкес келетін күктелерді координаттық жазықтықта белгілесек, X және У жиындарының злементерінің арасындағы “артық” сәйкестігінің графигін аламыз.

Жиындар арасындағы сәйкестік ұғымы математикадағы негізгі ұғымдардың қтарына жатады. Олай болатын себебі, бұл ұғым математикадағы функция және бейнелеу сияқты аса маңызды ұғымдарды анықтаудың негізі болып табылады.

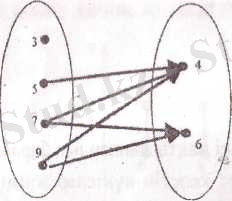
Х={3, 5, 7}, У ={4, 6} жиындарының элементтерінің арасында R -“артық” сәйкестігі берілсін. Сонда R ={(5, 4), (7, 4), (7, 6) } және графы (1-сызба) . Осы графтағы стрелкалардың бағытын кері өзгертейік. Сонда У жоне X жиындарының элементтерінің арасыңдағы "кем" сәйкестігінің графигі алынады

Сызбада графы кескінделген сәйкестік берілген R сәйкестігіне кері сәйкестік деп аталып, R ' арқылы белгіленеді.

Бастауыш мектептің математика курсында өзара кері сәйкестікке көп көңіл бөлінеді. Оқушылар 5>3 болғандықтан 3< 5 екенін, егер АВ кесіндісі СД кесіндісінен ұзын болса, онда СД кесіндісі АВ кесіндісінен қысқа болатынын терең түсіну керек.

Математиканың бастауыш курсында өзара бірмәнді сәйкестік ұғымы айқын түрде қолданылмайды: оған санау және сандарды салыстыру процесі негізделген. Мысалы, 3 = 3 тендігін түсіндіру үш қызыл, үш көк шаршыны алып, әрбір қызыл шаршыға бір көк шаршыны сәйкес қояды (шаршыны бір-біріне беттестіріп кояды, оларды кесінділермен қосады т. с. с. ), яғни қызыл және көк түсті шаршылар жиындары арасында өзара бірмәнді сәйкеспк орнатылады.

Жиындарды бейнелеу - сәйкестік ұғымының дербес жағдайы. X және У жиындары злементтерінің арасындағы Р сәйкестікте хеХ элементінің бейнесінің болмауы, сонымен қатар соның бейнесі болатын бірнеше элементтің болуы да мүмкін.

Анықтама. X жиынын У жиынының ішкі жиынына бейнелеу деп әрбір х∈Х элементінің бейнесі бір және тек бір ғана у∈У болатын X және У жиындары арасындағы сөйкестікті айтады. Басқа сөзбен айтқанда, кез келген х∈Х үшін хРу болатын бір және тек бір ғана у∈У табылады.

Бейнелеулер бірнеше түрге бөлінеді. Егер У жиынының әрбір элементі ең болмағанда Х-тің бір элементінің бейнесі болса, ондай бейнелеуді
сюръективті бейнелеу немесе X жиынын У жиынына бейнелеу деп атайды.

Егер У жиынының әрбір элементі Х-тің бірден артық емес элементінің бейнесі болса, ондай бейнелеуді инъективті бейнелеу немесе X жиынын У жиынының ішкі жиынына бейнелеу деп атайды.

Егер У-тің әрбір элементі Х-тің бір және тек қана бір элементінің бейнесі болса, яғни бейнелеу әрі сюръективті және инъективті болса, ондай бейнелеуді биективті бейнелеу деп атайды.

Егер f бейнелеуде әрбір у∈У элементтің толық түпкі бейнесі тек қана бір х∈Х элементтен тұрса, яғни әрбір у∈У элемент тек қана бір х∈Х элементтің бейнесі болса және тек сонда ғана f:х→у бейнелеуі өзара бір мөнді бейнелеу болып табылады.

Бақылау сұрақтары:

1. Сәйкестік.

2. Берілген сәйкестікке кері сәйкестік.

3. Сәйкестіктің анықталу облысы.

4. Жиындарды бейнелеу.

5. Сюръекттивті бейнелеу.

6. Инъективті бейнелеу.

7. Биективті бейнелеу.

8. Өзара бірмәнді бейнелеу.

9. Өзара бірмәнді сәйкестік.

10. Тең қуатты жиындар.

Жаттығу:

1. А={1, 2, 4, 6} және В={5, 7} жиындарының арасында “кем”, “1-і кем” сәйкестігі берілген. Берілген сәйкестіктің графын, графигін сыз. Кері сәйкестік құрастыр, графигін сыз.

2. Х={0, 1, 2, 3, 4, 5} және У=Ζ жиындары “х санының у санынан 3-кем” сәйкестігі берілген. Сәйкестіктің графигін сыз. Кері сәйкестік құрастыр, графигін сыз.

3. Х={2, 5} және У={3, 6}, ХхУ ішкі жиынын құрастыр. Қай ішкі жиын сәйкестік құрастырады?

4. Оқушылар қарындашқа 10теңне, дәптерге 7 теңге, өшіргішке 5 теңге, қаламға 15 теңге төледі. Қандай екі жиын арасында сәйкестік берілген.

5. Х={1, 2, 3}, У={1, 2, 34, 5, 6, 7} берілген жиындарға тең қуатты болатын жиындарға 3 мысал келтір.

6. Сатып алынған заттар есебі неде: кітап-120 тг, дәптер-5 тг, бояу жаққыш 20 тг, өшіргіш 15 тг. Сатып алынған заттар жиыны Х және осы заттардың бағаларының жиыны У-ті жазып, олардың арасындағы сәйкестікті тұжырымдап, оның графын құрыңыз.

7. Төбелерінің координаталары (0, 6), (5, 0), (0, -3), (8-, 0) бойынша төртбұрыш салыңыздар. Осы төртбұрыш Х (ені) және У (ұзындығы) жиындарының арасындағы сәйкестіктің графигі болып есептеледі.

Лекция 5.

Математикалық тұжырымдар және олардың құрылымы.

Математикалық ұғымдарды анықтаудың құрылымы.

Лекция мақсаты:

1. Математикалық ұғымдарды қарастыру.

2. Математикалық ұғымдарды анықтау тәсілдері.

Математика да басқа ғылымдар сияқты бізді қоршаған ортаны қоғамдық құбылыстарды зерттейді, бірақ олардың ерекше жақтарын қарастырады.

Математика өзінің тарихында әртүрлі даму кезеңінен өтті. Осы кезеңердің әрқайсысында әртүрлі пішіндер мен материалдық ортаның сандық қатынастарының белгілі бір әдістерін және ұғымдарды қалыптастырды.

Ұғым-материяның жоғары жемісі болып табылатын мидың жоғарғы жемісі. Әрбір ұғым мазмұны және көлемі бойьшша қарастырылуы мүмкін. Ұғым мазмұны-берілген ұғымның барлық (аса елеулі, маңызды) мәнді белгілерінің жиыны. Ұғым көлемі, ол -берілген ұғым қамтитын объектілердің жиыны.

Математикалық ұғымдармен оқушылар бастауыш мектептің математика курсында таныса бастайды. 1-сыныптан бастап оқушылар “цифр”, “сан”, “қосылғыш”, “қосынды”, “кесінді”, т. б. ұғымдармен танысады. 3-сыныпта оған көбейту мен бөлуге байланысты, ал 4-сыныпта “бөлік”, “фигураның ауданы” ұғымдары қосылады.

Демек, математикалық ұғымның (объектінің) анықтамасы - осы ұғымның мазмұнын ашатын сөйлем.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.