Индукция

Пән: Медицина
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Индукция.

Индукция деп әдетте жекеден жалпыға ѳтудегі ой қорыту түсініледі. Индукция туралы кең мағынада, ойлау қозғалысының жеке жағдайлардан жалпы жағдайга көшу нәтижесіндегі таным әдісі; тану амалы деп айтуға болады. Жалпы алғанда, математикада индуктивті әдіс деп тәжірибе арқылы тексерілген және дұрыстығы қатаң түрде тағайындалған теориялық сипаттағы айғақтар негізінде жаңа қорытындылар және теориялар алу деп түсініледі.

Математикада теоремаларды дәлелдеуде, есептерді шығаруда көп қолданылатын әдістердің бірі индукция мен дедукция деп аталады. Бұл әдістердің негізіне түсіну үшін алдымен ойды қорытындылаудың каңдай түрлері болатынын қарастырайық. Ойды тұжырымдаудың екі түрі болады. Мысалы, "120" саны 5-ке бөлінеді десек, тек бір ғана санның (120-ның), екінші бір санға (5-ке) бөлінетініи айттық, Сондықтан бұл жеке фактыны қарастыру арқылы жасалынған дербес тұжырым. Бөлінгіш (120) нольмен аяқталған үш таңбалы сан оның осы екі қасиетін байқап алып, мынадай жалпы екі ой қорытындысын жасайық:

1. Нольмен аяқталған сандардың барлығы 5-ке бөлінеді.

2. Үш таңбалы сандардың барлығы 5-ке бөлінеді.

Бұл екі пікірдің біріншісі дұрыс болғанымен, екіншісі бұрыс, өйткені үш таңбалы сандардың барлығы бірдей 5-ке бөліне бермейді.

Осындай жеке ой қорытындысынан жасалынған жалпы ой қорытындысын индукция (лат. іnductio-ой салу) деп атайды.

Сөйтіп, дербес фактыларды қарастырып, яғни индукция жолымен, жасалынған жалпы ой қорытындысы дұрыс та, теріс те болуы мүмкін. Енді ол кай уақытта дұрыс және қай уақытта теріс болатындығына көз жеткізу үшін индукцияның қандай түрлері болатынын карастырайык.

Индукция 3 түрлі болады:

1. Толымсыз индукция;

2. Толық индукция;

3. Математикалық индукция.

Толымсыз индукция .

Жеке фактылар ѳте кѳп болып, бірақ олардың барлығын қарастырмай, тек кейбіреулерін ғана қарастырып, олардағы ерекшеліктерді байқап алып, сол арқылы жалпы қорытынды жасайтын болсақ, ол толымсыз индукция болады.

Сонымен, толымсыз индукция дегеніміз зерттеліп отырған құбылыстың, объектілердің барлық жағдайларын қамтымайтын алғы шарттардан шығатын жалпы ой қорытындысы.

Толымсыз индукция жасаған қорытынды дұрыс болмауы мүмкін, өйткені алғашқы жеке фактыларда бар ерекшелік кейінгілерінде болмайтын жағдай болады. Сондықтан толымсыз индукция барлық жеке жағдайлар түгел қарастырылмағандықтан, бұған сүйеніп айтылған қорытынды дұрыс бола бермейді. Сондықтан бұл ғылыми дәлелдеудің қатаң түрі бола алмайды.

Мысалы, математика тарихынан толымсыз индукцияны қолданып теріс қорытындылар жасалынған жағдайларды көптеп кездестіреміз. Мысалы, француз математигі Ферма (1601-1665)

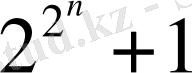формуладағы n -нің дербес ( n =1, 2, 3, 4) мәндерін қарастырып келіп, бұл саннан әрқашан жай сан шығады деп жорыған. Кейін оны Л-Эйлер (1707-1783) тексере келіп, n =5 болғанда жай сан болмайтынын тапқан.

Ерекшелігін Л. Эйлер көрсеткен ұш мүшедегі (х ² +х+41) х -ке қандай мән берілсе де, одан жай сан береді деп білген, бір кезде. Кейін х -тің дербес мәндерін тексере келіп, х=0, 1, . . . , 39 болғанда жай сан, ал х=40 болғанда құрама сан шығатыны байқалған.

Бірақ солай бола тұрса да толымсыз индукцияның ғылымда маңызы күшті. Оның пайдасы белгілі бір зерттеу мәселесінде кейбір жеке жағдайларды қарастыру арқылы сәйкес зандылыкты байқап, жалпы қорытыңдының қандай болатынын жобалауға болады.

Толық индукция.

Толық индукция дегеніміз-зерттеліп отырған құбылыстың немесе объектінің барлық жағдайларын толық қамтитын алғы шарттардан жалпы қорытынды шығаруға болатын индукциялық ой қорытыңдысы.

Мысалы, бір кластағы 30 оқушының әрқайсысының да сабақтан үлгеретіндігі тексеріліп анықталса, онда бұл жеке алғы шарттардан: "бұл кластың барлық оқушылары сабақтан үлгереді" деген дұрыс пікір айтуға болады.

Қорытып айтқанда, толық индукцияға сүйеніп айтылған ой қорытындысы әр-уақытта ақиқат болады.

Бірақ математикада толық индукцияны жиі қолдануға мүмкіндік бермейтін қолайсыз жағдай бар. Оның себебі, белгілі ой қорытындысын шығару үшін жоғарыдағы көрсетілгендей барлық жеке жағдайларды тексеру керек. Ал математикада ондай жеке жағдайлардың шексіз болып келетіні жиі кездеседі. Оңдай пікірлердің ақиқаттығына толық индукция арқылы көз жеткізу мүмкін емес.

Математикалық индукция

Математикалық индукция жасалған қорытынды бірнеше дербес жағдайлар үшін дұрыс болса, дербес жағдайлар өте көп болғандықтан олардың барлығын бірдей қарастыру мүмкін болмаса, бірақ сол қорытындының жалпы дұрыстығын қалайда білу керек болса, онда математикалық индукция әдісі қолданылады.

Математикалық индукция әдісінің негізіне мынадай принцип жатады.

Қаңдай да пікір

1. Натурал сан п=1 болғанда дұрыс болса және

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.