Жарық толқындары: теориясы мен негізгі оптикалық құбылыстар


Жарық толқындары
§ 4. 1 Жарық табиғатына көзқарастың дамуы
Жарық табиғатына деген адамдардың көзқарасы ерте заманнан ақ қалыптаса бастаған. Осыдан екi жарым мың жыл бұрын Пифагор «әрбiр зат өзiнен аса ұсақ бөлшектер шығарады, ол бөлшектер адам көзiне жетiп, адам заттарды көредi» деп түсiндiрген. Көптеген ғасырлар бойы үстемдiк құрған осы пiкiрдi И. Ньютон одан әрi дамытты. Ол жарық бөлшектерiн корпускулалар деп атап, бұл бөлшектер инерция заңын қанағаттандырады деп есептедi. Бұлай деу тәжiрибеден байқалатын жарықтың түзу сызық бойымен таралу, шағылу заңдарын түсiндiруге мүмкiндiк беретiн. Одан әрi жарық жөнiнде жаңа тәжiрибелiк деректердiң жинақталу барысында интерференция және дифракция тәрiздi құбылыстар ашылды. Бұл құбылыстарды жарықтың корпускулалық қасиетi арқылы түсiндiру мүмкiн емес едi. Осымен байланысты ХIХ ғасырдың басында Х. Гюйгенс, Ю. Юнг және О. Френель тәрiздi ғалымдардың еңбектерiнде жарықтың толқындық теориясы ұсынылып, қалыптасты.
Жарық жөнiндегi көптеген көкейтестi мәселелердiң шешiмi тек Максвелл ойлап тапқан электромагниттiк өрiстiң теориясынан кейiн ғана табылды. Бұл теориядан жарық дегенiмiз толқын ұзындығы белгiлi бiр аралықта жатқан электромагниттiк толқындар екендiгi шығатын.
Жарықтың табиғатын түсiнуде оның жылдамдығының шектi екендiгiн анықтаудың маңызы зор болды. Жарық жылдамдығын алғаш рет ХVII ғасырдың аяғында О. Ремер өлшеген болатын. Ремер әдiсi Юпитер планетасының серiгiнiң қозғалысын бақылауға негiзделген болатын.
§ 4. 2 Жарықтың шағылысу заңы. Жарықтың сыну заңы. Толық шағылу құбылысы
Тығыздығы өзгеретiн ортада тараған жарық өзiнiң түзусызықты қалыпынан ауытқып, таралу бағытын өзгертедi. Егер тығыздықтың мәнi екi ортаның шекарасында күрт өзгеретiн болса, онда бұл жерде жарықтың шағылысу және сыну құбылыстары байқалады. Мұндай орталардағы жарықтың таралу бағытын әдетте түсу, шағылу және сыну бұрыштары арқылы анықтайды.
Түсу бұрышы деп түскен сәуле мен түсу нүктесiне тұрғызылған перпендикулярдың арасындағы α бұрышын айтады. Сәйкес шағылу бұрышы α′ - шағылған сәуле мен осы перпендикулярдың, ал сыну бұрышы β? - сынған сәуле мен осы перпендикулярдың арасындағы бұрыштар ( 4. 1 - сурет ) .
Жарықтың шағылу заңы былай дейдi : Түскен сәуле, шағылған сәуле және түсу нүктесiне тұрғызылған перпендикуляр бiр жазықтықта жатады және түсу бұрышы шағылу бұрышына тең болады, яғни α=α′
Жарықтың сыну заңын тұжырымдамастан бұрын ортаның сыну көрсеткiшi ұғымын енгiзелiк. Ортаның абсолют сыну көрсеткiшi деп жарықтың вакуумдағы жылдамдығының оның осы ортадағы жылдамдығына қатынасын айтады, яғни
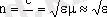
мұндағы ε және μ - ортаның салыстырмалы диэлектрлiк және магниттiк өтiмдiлiгi. Бұл өрнекте ферромагниттi емес кез-келген орта үшiн μ∼1 екенi ескерiлген.
Егер жарықтың сыну құбылысы вакуум мен ортаның шекарасында емес, қандай да бiр екi оптикалық ортаның шекарасында болса, онда екiншi ортаның бiрiншi ортаға қатысты салыстырмалы сыну көрсеткiшi n 21 деп жарықтың бiрiншi ортадағы жылдамдығының екiншi ортадағы жылдамдығына қатынасына тең мына шаманы айтады
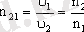
мұндағы n1 және n2 - сәйкес бiрiншi және екiншi орталардың абсолют сыну көрсеткiштерi.
Жарықтың сыну заңы былай дейдi : Түскен сәуле, сынған сәуле және түсу нүктесiне тұрғызылған перпендикуляр бiр жазықтықта жатады және түсу бұрышының синусының сыну бұрышының синусына қатынасы тұрақты шама, ол екi ортаның салыстырмалы сыну көрсеткiшiне тең болады, яғни
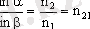
Ортаның абсолют сыну көрсеткiшi оның оптикалық тығыздығымен байланысты. Оптикалық тығыздықтың мәнi артқан сайын сыну көрсеткiшiнiң мәнi де артады. Егер жарық оптикалық тығыздығы кемдеу ортадан оптикалық тығыздығы артықтау ортаға өтсе, онда n 2 >n 1 , немесе n 21 >1. Ал бұдан sin α > sin β екендiгi шығады, яғни түсу бұрышы сыну бұрышынан әрқашанда үлкен.
Ал, керiсiнше, жарық оптикалық тығызырақ ортадан оптикалық тығыздығы кемдеу ортаға өтсе, онда сәйкес sin α < sin β, немесе α < β, яғни сыну бұрышы түсу бұрышынан үлкен. Бұл жағдайда егер түсу бұрышын бiртiндеп арттыра бастасақ, онда сыну бұрышы да арта отырып, α - ның қандай да бiр αшек -ге тең мәнiнде ол 90 0 -қа тең болады. Ал ендi α-ның мәнiн одан да әрi арттыратын болсақ, онда сынған сәуле екiншi ортаға өтпей сол бiрiншi ортада қалып қояды. Осы құбылысты толық iшкi шағылу құбылысы деп атайды. Шағылу және сыну заңдарының ерекшелiктерiн мына жерден көруге болады.
§ 4. 3 Жарық дисперсиясы. Дисперсия құбылысын бақылау
Ақ жарық шыны призмадан өткен кезде бiрнеше түске жiктелетiнiн алғаш рет И. Ньютон бақылап, зерттеген болатын. Мұндай монохроматты ( бiр түстi, мысалы, қызыл, көк, күлгiн т. с. с. ) жарық одан әрi басқа түстерге жiктелмейдi. Ал ендi осылай ақ жарықтың монохроматты жарықтарға жiктелуiнiң себебi неде ? Ол мынада. Жарық дегенiмiз - электромагниттiк толқындар. Әртүрлi түстегi жарықтар бiр-бiрiнен толқын ұзындығының, немесе онымен байланысты жиiлiгiнiң әртүрлi болуымен өзгешеленедi. Ал жарықтың шыны призмадан өткенде әртүрлi түске жiктелуiнiң себебi қандай да бiр ортадағы жарық жылдамдығының ( немесе онымен байланысқан сыну көрсеткiшiнiң ) жарық жиiлiгiнен тәуелдiлiгiмен байланысты. Сыну көрсеткiшiнiң жарық жиiлiгiнен осындай тәуелдiлiгiн дисперсия құбылысы деп атайды (4. 2 - сурет) . Бұл құбылысты түсiндiруге Максвеллдiң электромагниттiк теориясын қолдану оң нәтиже бермедi.

Себебi бұл жердегi мәселе тек электромагниттiк толқынның қасиетiнде ғана емес, сонымен қатар ол толқындардың затпен әсерлесу сипатымен де байланысты болатын.
Дисперсия құбылысын ХIХ ғасырдың аяғында қалыптасқан Г. Лоренцтiң классикалық электрондық теориясы ғана түсiндiрiп бере алды. Бұл теорияның түсiндiруi бойынша жарықтың дисперсиясы зат атомдарындағы электрондардың электромагниттiк өрiспен әсерлесуiнiң нәтижесiнде туындылайтын ерiксiз тербелiсiнiң нәтижесi болып табылады. Осы теорияның негiзiнде табылған дисперсия заңы (сыну көрсеткiшiнiң жиiлiктен тәуелдiлiгi) мынадай:
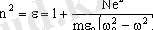
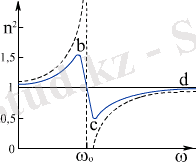
мұндағы N - молекулалар концентрациясы, e - элементар заряд, m - электронның массасы, ε 0 - электр тұрақтысы, ω 0 - электронның өзiндiк жиiлiгi, ω - сыртқы электромагниттiк өрiстiң жиiлiгi. Бұл тәуелдiлiктiң сызбасы 4. 3 - суретте келтiрiлген. Мұндағы үзiк сызық ( 4. 4 ) өрнегiмен есептелген дисперсияның теориялық тәуелдiлiгiне, ал тұтас сызық тәжiрибенiң нәтижесiне сәйкес келедi. Бұл суреттегi жиiлiк артқан кездегi сыну көрсеткiшi де артатын, өзiндiк жиiлiктiң мәнiнен тысқары жатқан ab және cd аймағы дұрыс дисперсия деп аталады. Ал өзiндiк жиiлiктiң маңында жатқан bc аймағында, керiсiнше, жиiлiк артқан кезде сыну көрсеткiшi кемидi. Бұл аномальдi дисперсия аймағы. Тәжiрибе бұл аймақта жарық затқа қатты жұтылатындығын көрсетедi. Бұл оның резонансты құбылыстармен терең байланыста екендiгiнiң дәлелi.
§ 4. 4 Жарық интерференциясы. Жұқа қабыршықтағы жарық интерференциясы. Интерференцияның техникада қолданылуы
Жарық бiр мезгiлде бiр емес бiрнеше көзден тарауы мүмкiн. Осылай әртүрлi жарық көзiнен шыққан толқындар бiр-бiрiмен қабаттасқан кезде қандай құбылыс байқалатынын қарастыралық. Кеңiстiктiң берiлген нүктесiне бiр мезгiлде екi жарық көзiнен шыққан толқындар келiп жетсiн делiк. Толқын теңдеулерi :
E 1y =E m cos (ω - k 1 r 1 + φ 1 )
E 2y =E m cos (ω - k 2 r 2 + φ 2 )
Мұндағы k 1 = 2πn 1 / λ және k 2 = 2πn 2 /λ сәйкес толқындық сандар, ал n 1 және n 2 жарық тарап жатқан орталардың сыну көрсеткiштерi. Бұл жерде есептеулердi жеңiлдету үшiн тербелiс амплитудаларын және жиiлiктерiн бiрдей етiп алдық. Ендi кеңiстiктiң берiлген нүктесiнде осы екi толқынның қабаттасуынан пайда болған қортқы тербелiстi табалық. Ол үшiн элементер математика курсынан белгiлi тригонометриялық өрнектердi пайдалана отырып, мынаны аламыз:
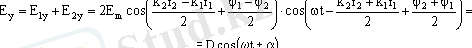
Мұндағы
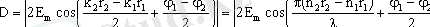
қортқы тербелiстiң амплитудасы, ал
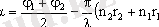
бастапқы фазасы. Амплитуданың өрнегiндегi Δ=n 2 r 2 - n 1 r 1 шамасын оптикалық жол айырымы деп атайды. Егер екi толқын да бiр оптикалық ортада тараса, онда n 1 =n 2 , ал одан Δ=r 2 - r 1 , яғни оптикалық жол айырымы геометриялық жол айырымына тең.
Жарықтың берiлген нүктедегi интенсивтiлiгi осы нүктедегi тербелiс амплитудасының квадратына пропорционал екендiгi белгiлi, яғни
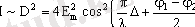
Бұл өрнектен қортқы интенсивтiлiктiң толқындардың Δ жол айырымына және δ=φ 1 - φ 2 фазалар айырымына тәуелдi екенi көрiнiп тұр. Бiр-бiрiнен тәуелсiз жарық шығарып тұрған көздер үшiн δ фазалар айырымы кездейсоқ түрде өзгередi. Ал аргументi кездейсоқ өзгерген косинустың квадратының орташа мәнiнiң 1/2 ге тең екенiн ескерсек, онда бұл жағдайдағы жарық интенсивтiлiгi үшiн
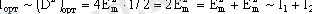
өрнегiн аламыз. Яғни, берiлген нүктедегi интенсивтiлiк әрбiр жеке көздерден түскен жарықтың интенсивтiлiктерiнiң қарапайым қосындысына тең.
Ендi екi жарық көзiнен шыққан толқындардың фазалар айырымы тұрақты болып қалсын делiк, яғни δ=φ
1
-φ
2
=const. Мұндай фазалар айырымы уақытқа қатысты өзгермейтiн жарық көздерiн
когеренттi
жарық көздерi деп атайды Онда, жоғарыдағы жарық интенсивтiлiгiнiң берiлген нүктедегi мәнi тек Δ жол айырымы арқылы ғана анықталады. . Дербес жағдайда δ=φ
1
-φ
2
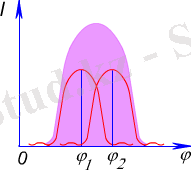
=0 деп алсақ, (4. 5) өрнегiнен берiлген нүктедегi жарық интенсивтiлiгiнiң мәнiнiң
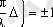 болғанда максимальдi, ал
болғанда максимальдi, ал
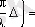 болғанда минимальдi екенi көрiнiп тұр. Ал бұл шарттардан жол айырымына қатысты мына шарттар шығады : Δ=mλ болғанда интенсивтiлiк максимальдi, ал Δ=(2m+1) ·λ/2 болғанда интенсивтiлiк минимальдi. Және де ең маңыздысы бұл интенсивтiлiктiң мәндерi уақытпен байланысты өзгермейдi, яғни тұрақты интерференциялық сурет аламыз.
болғанда минимальдi екенi көрiнiп тұр. Ал бұл шарттардан жол айырымына қатысты мына шарттар шығады : Δ=mλ болғанда интенсивтiлiк максимальдi, ал Δ=(2m+1) ·λ/2 болғанда интенсивтiлiк минимальдi. Және де ең маңыздысы бұл интенсивтiлiктiң мәндерi уақытпен байланысты өзгермейдi, яғни тұрақты интерференциялық сурет аламыз.
Мiне осылай когеренттi толқындардың қабаттасуының салдарынан кеңiстiктiң әрбiр нүктесiнде жарық интенсивтiлiгiнiң күшейiп, не бәсеңсуiнiң уақыт бойынша өзгермейтiн орнықты бейнесiн алу жарық интерференциясы деп аталады.
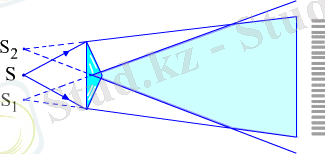
Жоғарыда анықтағанымыздай орнықты интерференциялық суреттi алудың негiзгi шарты жарық көздерiнiң когеренттi болуы. Алайда, жарықтың шығуы жекелеген атомдарда өтетiн процесстермен байланысты болғандықтан, табиғи жарық көздерi бiр-бiрiне ешқашанда когеренттi болмайды. Сондықтан, әдетте интерференциялық суреттi бiр жарық көзiнен шыққан толқындарды екiге жiктеп, қайтадан қабаттастыра отырып алады.
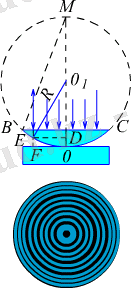
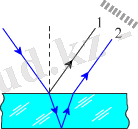
Оның мысалдары Френельдiң қос призмасы (4. 4 - сурет), Ньютон сақиналары (4. 5 - сурет) және жұқа қабыршықтағы интерференция (4. 6 - сурет) . Жұқа қабыршықтағы интерференцияны бiз сабын көпiршiктерiнiң немесе асфальттағы шалшық бетiне тамған майда түрлi-түстi болып құбылып тұратын дақ түрiнде байқаймыз. Мұның себебi қабыршыққа түскен жарық оның жоғарғы және төменгi беттерiнен шағыла отырып, бiр-бiрiмен қабаттасып интерференцияланады.
Интерференция құбылысы әртүрлi зерттеу жұмыстарында өте дәл өлшеулер жүргiзуге мүмкiндiктер бередi. Себебi, мұндай өлшеулер кезiнде жарықтың толқын ұзындығымен шамалас болатын өте аз өзгерiстiң өзi интерференциялық суретте өлшеуге болатын елеулi ығысуларға алып келедi. Интерференция құбылысын пайдалана отырып өлшеулер жүргiзуге арналған құралдарды интерферометрлер деп атайды. Алғашқы жасалған мұндай құралдардың бiрi Майкельсон интерферометрi. 1887 жылы А. Майкельсон және Э. Морли осы құралдың көмегiмен "жарықтың жылдамдығына Жер қозғалысының әсерi бола ма?" деген сұраққа жауап iздеген әйгiлi тәжiрибесiн жасады. Эйнштейннiң салыстырмалы теориясын жасауда бұл тәжiрибенiң шешушi роль атқарғаны ғылым тарихынан белгiлi.
Интерференция құбылысы сонымен қатар әртүрлi беттердiң өңделу сапасын тексеруге, оптикалық құралдарда жарықтың әртүрлi линзалардың бетiнен шағылып, бейненiң сапасының төмендеуiн болдырмауға т. с. с. қолданылады.
§ 4. 5 Жарық дифракциясы. Дифракциялық тор
Жарық дифракциясы деп жарық толқындарының өзiнiң алдында кездескен кедергiлердi орап өту қабiлетiн айтады. Дифракция құбылысы жарықтың толқындық қасиетiнiң айқын дәлелi болып табылады. Бұл құбылыс геометриялық оптика заңдылықтарының қай кезде бұзылатындығына нұсқайды.
Дифракцияның сандық теориясы, яғни бұл құбылыстың әсерiнен экрандағы жарық интенсивтiлiгiнiң өзгерiп таралуын түсiндiру Гюйгенс-Френель принципiне негiзделген. Бұл принцип былай дейдi :
1. Жарық толқындары келiп жеткен беттiң әрбiр нүктесi өз кезегiнде жаңа толқын көздерi болып табылады
2. Бұл жаңа толқын көздерi бiр-бiрiне когеренттi. Ал кеңiстiктiң кез-келген нүктесiндегi жарықтың интенсивтiлiгi осы когеренттi жаңа көздерден тараған толқындардың интерференциясының салдары болып табылады.
Гюйгенс-Френель принципi дифракциялық бейнелермен қатар жарықтың түзу сызық бойымен таралу себебiн де түсiндiредi.
Жарық дифракциясының бiр жарқын мысалы оның тар жолақ саңлау арқылы өткен кездегi дифракциясы. Бiрақ, бұл жағдайдағы дифракциялық суреттiң солғындау болуы оны нақтылы мақсаттарда қолдануда қиындықтар туғызады. Мұндай кемшiлiктер дифракциялық тор деп аталатын қондырғыда жоқ.
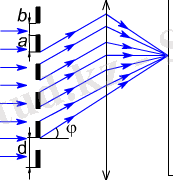
Дифракциялық тор деп бiр-бiрiне жақын, әрi параллель орналасқан тар жолақ саңлаулар жүйесiнен тұратын спектральдық құралды айтады (4. 7 - сурет ) . Мұндағы a - күңгiрт жолақтың енi, b - саңлаудың енi, ал d=a+b - дифракциялық тордың тұрақтысы деп аталады.
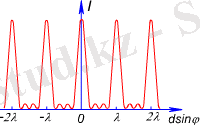
Қазiргi кезде қолданылатын дифракциялық торлардың бiр миллиметрiне 2000-ға дейiн саңлаулар салынады. Гюйгенс-Френель принципiне сәйкес мұндай әрбiр саңлау өз кезегiнде жаңа когеренттi толқын көздерi болып табылады да бұл көзден туындылаған толқындар бiр-бiрiмен интерференцияланады. Егер дифракциялық торға перпендикуляр бағытта параллель жарық сәулелерi түсетiн болса, онда линзаның фокальдық жазықтығында орналасқан экранда қандай да бiр φ бұрышымен дифракциялық максимумдар байқалады. 4. 8-суреттен көрiнiп тұрғанындай бұл максимумдар мынадай шарттарды қанағаттандырады
мұндағы n=0, 1, 2, … - бас максимумдар ретi деп аталады.
Дифракциялық торлар жарықты спектрлерге жiктеу үшiн, сонымен қатар жарықтың белгiсiз толқын ұзындығын анықтау үшiн де қолдаылады. Нақтылы зерттеулерде бiр өлшемдi торлармен қатар екi өлшемдi торлар да жиi қолданылады. Екi өлшемдi торлар деп жолақтарын бiр-бiрiне перпендикуляр орналастырып, беттестiрген екi жәй тордан тұратын жүйенi айтады. Мұндай жүйеден өткен жарық 4. 9 - суреттегiдей болып дифракцияланады.
§ 4. 6 Электромагниттiк сәуле шығарудың шкаласы. Осы сәулелердiң қасиеттерi және оны пайдалану
Қоршаған орта жөнiндегi бiлiмiмiздiң тереңдеуiнiң барысында алғашқы кезде бiр-бiрiнен тәуелсiз болып көрiнген көптеген құбылыстардың арасында терең байланыс бар екенi белгiлi болды. Соның бiр мысалы жарық, рентген сәулелерi және радиотолқындардың арасындағы байланыс. Бұл күнде бұл физикалық нысандардың бәрiнiң табиғатының бiр - олардың бәрiнiң электромагниттiк толқын екенi, олардың бiр-бiрiнен тек толқын ұзындығының мәнiмен ғана ажыратылатыны белгiлi. 4. 10 - суретте электромагниттiк сәуле шығарудың шкаласы келтiрiлген. Ол өте кең ауқымды қамтиды.

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz