Матрицалар мен анықтауыштар, матрицаларға амалдар, сызықтық теңдеулер жүйелері және векторлар


Матрицалар. Екінші және үшінші ретті анықтауыштар. Анықтауыштардың қасиеттері
Анықтама.
 өлшемді матрица деп,
өлшемді матрица деп,
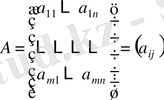 (1)
(1)
түріндегі
 - жол (жатық жол) және
- жол (жатық жол) және
 - бағаннан (тік жолдан) тұратын
- бағаннан (тік жолдан) тұратын
 - түріндегі сандар кестесін айтады.
- түріндегі сандар кестесін айтады.
 - сандары оның элементтері деп аталады. Мұндағы 1 - ші индекс осы элемент тұрған жол нөмірін, ал 2 - ші индекс баған нөмірін білдіреді.
- сандары оның элементтері деп аталады. Мұндағы 1 - ші индекс осы элемент тұрған жол нөмірін, ал 2 - ші индекс баған нөмірін білдіреді.
 болса, онда (1) - квадрат матрица деп аталады. бұл жағдайда
болса, онда (1) - квадрат матрица деп аталады. бұл жағдайда
 (немесе
(немесе
 ) саны оның ретін көрсетеді.
) саны оның ретін көрсетеді.
 - ші ретті квадрат матрица
- ші ретті квадрат матрица
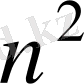 элементтен тұратыны түсінікті.
элементтен тұратыны түсінікті.
Матрица - ғылыми-техникалық және экономикалық есептерде кестелік ақпараттарды жазу үшін қолданылады; бағдарламалау саласында матрицаларды екі өлшемді массивтер деп атайды.
Кейде ыңғайлы болу үшін матрицаның өлшемін индекске жазады:
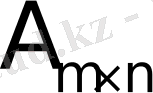 .
.
 өлшемді
өлшемді
 және
және
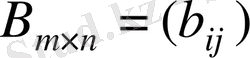 матрицаларының сәйкес элементтері тең болса, (
матрицаларының сәйкес элементтері тең болса, (
 ), онда олар тең матрицалар деп аталады да
), онда олар тең матрицалар деп аталады да
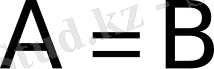 деп белгіленеді.
деп белгіленеді.
Квадрат матрица үшін осы матрицадан туындаған анықтауыш матрица анықтауышы деп аталатын
 санын қарастыруға болады. Кейде анықтауыш
санын қарастыруға болады. Кейде анықтауыш
 (ағыл. Детерминант-анықтауыш) немесе
(ағыл. Детерминант-анықтауыш) немесе
 арқылы белгіленеді.
арқылы белгіленеді.
2 - ші ретті матрица анықтауышы деп
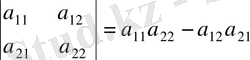 (2)
(2)
санын айтады.
3 - ші ретті матрица анықтауышы деп
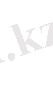
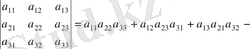
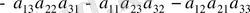 (3)
(3)
санын айтады. (3) анықтауыштың мәнін үшбұрыш ережесі арқылы есептейік. Оны еске ұстау үшін келесі схемалық жазу пайдаланылады:
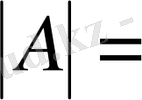 + + + _ _ _
+ + + _ _ _
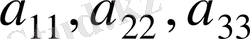 - элементтері орналасқан кесінді анықтауыштың бас диагоналі, ал
- элементтері орналасқан кесінді анықтауыштың бас диагоналі, ал
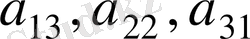 - элементтері орналасқан кесінді оның бүйір диагоналі деп аталады.
- элементтері орналасқан кесінді оның бүйір диагоналі деп аталады.
Анықтама.
 матрицасының жолдарын сәйкес бағандар етіп орнын алмастырудан алынған
матрицасының жолдарын сәйкес бағандар етіп орнын алмастырудан алынған
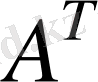 матрицасы
матрицасы
 матрицасының транспонирленген матрицасы деп аталынады.
матрицасының транспонирленген матрицасы деп аталынады.
 мен
мен
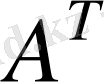 матрицаларының элементтері бас диагоналға салыстырғанда симметриялы орналасқан.
матрицаларының элементтері бас диагоналға салыстырғанда симметриялы орналасқан.
Жолдарды бағандармен алмастыру амалы транспонирлеу деп аталады.
 aнықтауышынан транспонирлеу арқылы алынған анықтауышты
aнықтауышынан транспонирлеу арқылы алынған анықтауышты
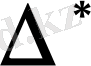 арқылы белгілейтін боламыз.
арқылы белгілейтін боламыз.
Енді анықтауыштардың қасиеттерін қарастырайық. Түсінікті болу үшін оларды 3 - ші ретті анықтауыштар үшін тұжырымдаймыз, алайда бұл қасиеттер реті кез келген анықтауыш үшін орындалады.
Кейбір жағдайларда сөйлем ықшамырақ болу үшін “жол немесе баған” деген сөзді “қатар” деп атайтын боламыз.
1 º . Транспонирленген анықтауыштың мәні өзгермейді:
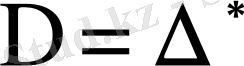 ,
,
яғни
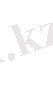

2 º . Анықтауыштың екі параллель қатарын орнын алмастырғаннан (бұл амал екі параллель қатарды транспозициялау деп аталады) анықтауыштың таңбасы өзгереді.
3 º . Параллель екі қатары бірдей (сәйкес элементтері тең) анықтауыш нөлге тең.
4. Егер қандай да бір қатардың барлық элементтері
 санына көбейтілсе, онда анықтауыш мәні
санына көбейтілсе, онда анықтауыш мәні
 санына көбейтіледі, басқаша айтқанда, қатардың ортақ көбейткішін анықтауыш таңбасының алдына шығаруға болады.
санына көбейтіледі, басқаша айтқанда, қатардың ортақ көбейткішін анықтауыш таңбасының алдына шығаруға болады.
Салдар. Егер екі параллель қатарлардың сәйкес элементтері пропорционал болса, онда анықтауыш нөльге тең.
5 º . Егер анықтауыштың қандай да бір қатарының барлық элементтері нөлге тең (нөл қатар) болса, онда анықтауыш мәні нөльге тең.
 Бұл қасиет 4
º
- тен
Бұл қасиет 4
º
- тен
 үшін алынады.
үшін алынады.
6 º . Егер анықтауыштың белгілі бір қатарының әрбір элементі екі қосылғыштың қосындысы етіп берілсе, онда анықтауыш екі анықтауыштың қосындысына тең. Бірінші анықтауыштың сәйкес қатары бірінші қосылғыштардан, ал екінші анықтауыштың сәйкес қатары екінші қосылғыш-тардан тұрады да, бұл екі анықтауыштың қалған сәйкес қатарлары өзара тең элементтерден тұрады.
7
º
. Егер анықтауыштың қандай да бір қатарының барлық элементтеріне осы қатарға параллель қатардың сәйкес элементтерін кез келген
 санына көбейтіп қосса анықтауыш мәні өзгермейді.
санына көбейтіп қосса анықтауыш мәні өзгермейді.
 Бұл қасиеттің дұрыстығын 6
º
, 4
º
және 3
º
қасиеттерді қолдана отырып көз жеткізуге болады.
Бұл қасиеттің дұрыстығын 6
º
, 4
º
және 3
º
қасиеттерді қолдана отырып көз жеткізуге болады.
2. Минорлар мен алгебралық толықтауыштар
Анықтауышты жол немесе баған элементтері бойынша жіктеу.
Анықтама.
 квадрат матрицасының
квадрат матрицасының
 - элементінің миноры деп
- элементінің миноры деп
 элементі тұрған жол мен бағанды алып тастап
элементі тұрған жол мен бағанды алып тастап
 матрицасының қалған қатарларынан құралған матрицаны айтады.
матрицасының қалған қатарларынан құралған матрицаны айтады.
 - ші ретті
- ші ретті
 матрицасының
матрицасының
 элементінің миноры реті “
элементінің миноры реті “
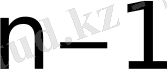 ” тең квадрат матрица болады. Oны
” тең квадрат матрица болады. Oны
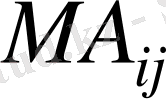 арқылы белгілейміз.
арқылы белгілейміз.
Минор түсінігін анықтауыштар үшін де қолданады. Анықтауыштың
 элементінің минорын
элементінің минорын
 арқылы белгілесек, онда
арқылы белгілесек, онда
 =
=
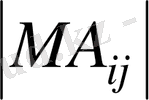 .
.
Мысалы:
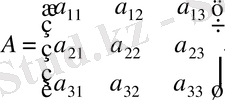 болса,
болса,
онда
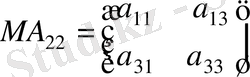 ,
,
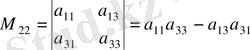 .
.
Анықтама.
 элементінің алгебралық толықтауышы немесе адъюнкті деп
элементінің алгебралық толықтауышы немесе адъюнкті деп
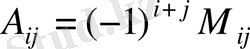
санын айтады.
8 º . Анықтауыштың қандай да бір қатарының элементтері мен олардың алгебралық толықтауыштарының көбейтінділерінің қосындысы осы анықтауыш шамасына тең:
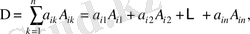
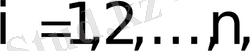 (1)
(1)
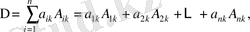
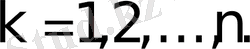 (2)
(2)
(1) - қосынды анықтауыштың
 -ші жол элементтері бойынша жіктелуі, ал (2) - қосынды анықтауыштың
-ші жол элементтері бойынша жіктелуі, ал (2) - қосынды анықтауыштың
 - шы баған элементтері бойынша жіктелуі деп аталады.
- шы баған элементтері бойынша жіктелуі деп аталады.
9 º . Анықтауыштың қандайда бір қатар элементтерімен осы қатарға параллель басқа бір қатардың сәйкес элементтерінің алгебралық толықтауыштарының көбейтінділерінің қосындысы нөлге тең.
3. Матрицаларға амалдар қолдану
Матрицаларға жасалатын келесі амалдарды қарастырамыз: санға көбейту, қосу, көбейту және кері матрица табу.
Алдымен келесі түсініктерді енгізейік.
Квадрат матрицаның бас диагоналінің сыртындағы (бас диагональ элементтерінен басқа) элементтердің барлығы нөлге тең болса, оны диагональдік матрица дейді.
 - ші ретті диагональдік матрицаны келесі түрде жазуға болады
- ші ретті диагональдік матрицаны келесі түрде жазуға болады
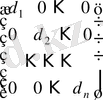 .
.
Егер мұнда
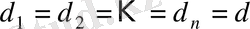 болса, онда
болса, онда
 және
және
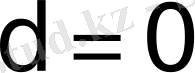 үшін диагональдік матрица сәйкес бірлік матрица және нөлдік матрица деп аталады:
үшін диагональдік матрица сәйкес бірлік матрица және нөлдік матрица деп аталады:
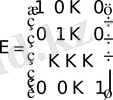 ,
,
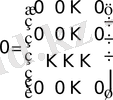 .
.
Ескерту. Нөлдік матрица түсінігі кез келген тік бұрышты (квадрат емес) матрицалар үшін де енгізіледі.
Анықтама.
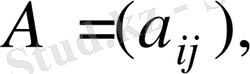
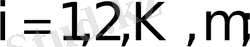
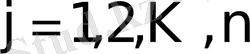 матрицасы мен
матрицасы мен
 санының көбейтіндісі
санының көбейтіндісі
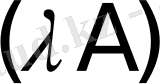 деп әрбір элементі
деп әрбір элементі
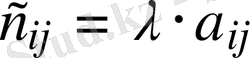 тең
тең
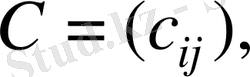
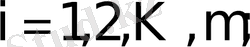
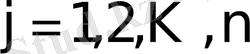 матрицасын айтады.
матрицасын айтады.
Бұл амал үшін келесі қасиеттер орындалады:
1)
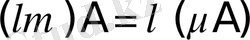 - сандық көбейткіштерге қатысты ассоциативті;
- сандық көбейткіштерге қатысты ассоциативті;
2)
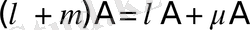 - сандарды қосуға қатысты дистрибутивті.
- сандарды қосуға қатысты дистрибутивті.
Сонымен бірге

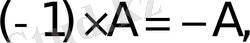
 теңдіктері орындалады.
теңдіктері орындалады.
Анықтама.
Бірдей өлшемді
 мен
мен
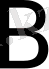 матрицаларының қосындысы деп әрбір элементі
матрицаларының қосындысы деп әрбір элементі
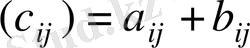 тең, өлшемі
тең, өлшемі
 немесе
немесе
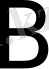 өлшеміндей,
өлшеміндей,
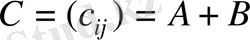 матрицасын айтады.
матрицасын айтады.
Матрицаларды қосу амалы үшін келесі қасиеттер орындалады:
1)
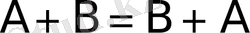 - коммутативтік;
- коммутативтік;
2)
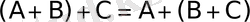 - ассоциативтік;
- ассоциативтік;
3)
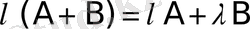 - матрицаларды қосуға қатысты дистрибутивтік.
- матрицаларды қосуға қатысты дистрибутивтік.
Анықтама.
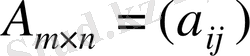 және
және
 матрицаларының көбейтіндісі деп элементтері
матрицаларының көбейтіндісі деп элементтері
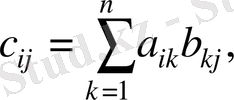
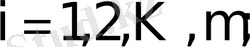
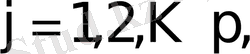 (1)
(1)
яғни
 - ші жол мен
- ші жол мен
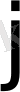 - ші баған қиылысуындағы
- ші баған қиылысуындағы
 элементі
элементі
 матрицасының
матрицасының
 - ші жолы мен
- ші жолы мен
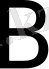 матрицасының
матрицасының
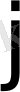 - ші бағанының сәйкес элементтерінің қос-қостан көбейтінділерінің қосындысына тең болатын
- ші бағанының сәйкес элементтерінің қос-қостан көбейтінділерінің қосындысына тең болатын
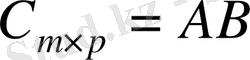 матрицасын айтады.
матрицасын айтады.
Ескерту. Анықтамадан 1 - ші матрицаның бағандар саны 2 - ші матрицаның жолдар санына тең болатын матрицаларды ғана көбейтуге болатынын көреміз.
Бұл мысалдан
 , яғни матрицаларды көбейту коммутативті емес екені көрінеді.
, яғни матрицаларды көбейту коммутативті емес екені көрінеді.
Матрицаларды көбейту амалы келесі қасиеттерге ие:
1)
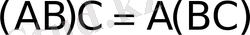 - ассоциативті;
- ассоциативті;
- және матрицаларды қосуға қатысты дистрибутивті;
3) Квадрат матрицалар үшін
 яғни көбейтінді анықтауышы көбейткіштер анықтауыштарының көбейтіндісіне тең.
яғни көбейтінді анықтауышы көбейткіштер анықтауыштарының көбейтіндісіне тең.
Сонымен бірге кез келген квадрат
 матрица үшін
матрица үшін

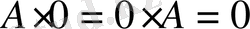 ,
,
яғни бірлік матрица
 бірлік сан сияқты, ал нөлдік матрица нөл саны сияқты роль атқарады.
бірлік сан сияқты, ал нөлдік матрица нөл саны сияқты роль атқарады.
Анықтама.
Егер
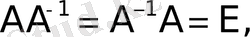
 - бірлік матрица, теңдіктері орындалса, онда
- бірлік матрица, теңдіктері орындалса, онда
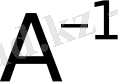 матрицасы
матрицасы
 матрицасына кері деп аталады.
матрицасына кері деп аталады.
Анықтама. Анықтауышы нөлге тең емес квадрат матрица нұқсансыз (невырожденной), ал анықтауышы нөлге тең квадрат матрица нұқсанды (вырожденной) деп аталады.
Ескерту. “Нұқсанды” немесе “нұқсансыз” түсініктері тек қана квадрат матрицалар үшін ғана қолданылатынын ескертеміз.
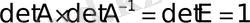 теңдігінен нұқсанды матрица үшін кері матрица болмайтыны шығады (
теңдігінен нұқсанды матрица үшін кері матрица болмайтыны шығады (
 ) .
) .
Анықтама.
 квадрат матрицасы берілсе, онда оның
квадрат матрицасы берілсе, онда оның
 элементтерінің алгебралық
элементтерінің алгебралық
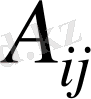 толықтауыштарынан құралған
толықтауыштарынан құралған
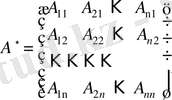
матрицасын тіркелген матрица деп атайды.
Тіркелген матрицаны алу үшін
 матрицасының әрбір элементін оның алгебралық толықтауышымен ауыстырып, алынған матрицаны транспонирлеу керек.
матрицасының әрбір элементін оның алгебралық толықтауышымен ауыстырып, алынған матрицаны транспонирлеу керек.
4. Кері матрица туралы
Теорема. Нұқсансыз матрицалардың, тек қана солардың кері матрицалары бар және кері матрица
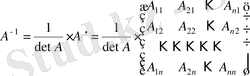 (2)
(2)
формуласы бойынша табылады.
5. Матрица рангі
Анықтама.
 матрицасының
матрицасының
 - шы ретті миноры деп
- шы ретті миноры деп
 матрицасының кез келген
матрицасының кез келген
 жолы мен кез келген
жолы мен кез келген
 бағандарының қиылысуындағы элементтерінен құралған матрицаны айтады.
бағандарының қиылысуындағы элементтерінен құралған матрицаны айтады.
Анықтама.
 матрицасының рангі деп осы матрицаның нұқсансыз минорларының ең үлкен ретін айтады да
матрицасының рангі деп осы матрицаның нұқсансыз минорларының ең үлкен ретін айтады да
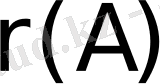 немесе
немесе
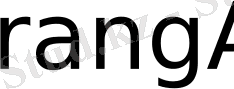 символдарының біреуімен белгілейді.
символдарының біреуімен белгілейді.
Нөлдік матрица рангі нөлге тең деп есептеледі.
Егер
 матрицасы
матрицасы
 - ші ретті нұқсансыз квадрат матрица болса, онда
- ші ретті нұқсансыз квадрат матрица болса, онда
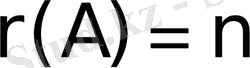 ; нұқсанды, яғни
; нұқсанды, яғни
 болса, онда
болса, онда
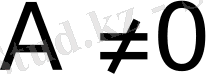 үшін
үшін
 ;
;
 матрицасы
матрицасы
 өлшемді матрица болса, онда
өлшемді матрица болса, онда
 .
.
Матрица рангін табу үшін оның 1 -ші ретті минорынан бастап барлық минорларын нұқсансыздыққа зерттесе болғаны.
5-8 дәріс
Тақырыбы: Сызықтық теңдеулер жүйесін шешу әдістері.
1. Сызықтық алгебралық теңдеулер жүйесі (САТЖ) .
Матрицалық әдіс және Крамер ережесі
Анықтама.
 белгісізі бар
белгісізі бар
 сызықтық алгебралық теңдеулер жүйесі (САТЖ) келесі түрде жазылады
сызықтық алгебралық теңдеулер жүйесі (САТЖ) келесі түрде жазылады
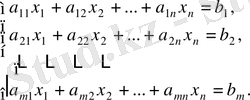 (1)
(1)
Мұнда
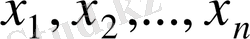 айнымалылары жүйенің белгісіздері,
айнымалылары жүйенің белгісіздері,
 ,
,
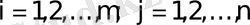 жүйе коэффициенттері; ал
жүйе коэффициенттері; ал
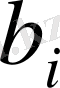 ,
,
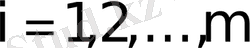 бос мүшелер деп аталады. Жүйенің барлық теңдеулерін тепе-теңдікке айналдыратын
бос мүшелер деп аталады. Жүйенің барлық теңдеулерін тепе-теңдікке айналдыратын
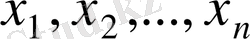 сандары жүйенің шешімі деп аталады. Егер жүйенің шешімі бар болса, онда ол үйлесімді, ал шешімі болмаса, онда ол үйлесімсіз жүйе деп аталады.
сандары жүйенің шешімі деп аталады. Егер жүйенің шешімі бар болса, онда ол үйлесімді, ал шешімі болмаса, онда ол үйлесімсіз жүйе деп аталады.
(1) - дегі белгісіздер коэффициенттерінен құралған
 өлшемді матрицаны
өлшемді матрицаны
 арқылы (оны жүйе матрицасы деп атайды)
арқылы (оны жүйе матрицасы деп атайды)
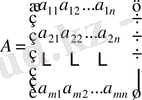 ,
,
бос мүшелері бағанын
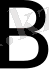 арқылы,
арқылы,
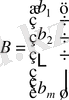 ,
,
ал белгісіздер бағанын
 арқылы
арқылы
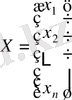 белгілейік.
белгілейік.
Онда (1) САТЖ матрицалық түрде жазуға болады:
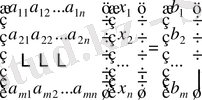 ,
,
немесе қысқаша
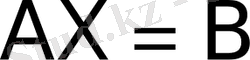 . (2)
. (2)
Егер
 квадрат матрица болса, онда жүйенің матрицалық түрінен кері матрицаны пайдаланып оның шешімін табуға болады.
квадрат матрица болса, онда жүйенің матрицалық түрінен кері матрицаны пайдаланып оның шешімін табуға болады.
Теорема. САТЖ - нің матрицасы нұқсансыз болса, онда оның жалғыз шешімі бар және ол келесі формуламен есептеледі:
 . (3)
. (3)
САТЖ - сін (3) формула арқылы шешу матрицалық әдіс деп аталады. Жүйенің Крамер ережесі деп аталатын басқа да түрде шешуін көрсетейік. (1) - С. А. Т. Ж.
 - ші ретті квадрат матрицасының детерминанты нөлге тең емес:
- ші ретті квадрат матрицасының детерминанты нөлге тең емес:
 болсын. Онда (1) - жүйенің жалғыз шешімі бар және ол келесі формулалар арқылы табылады:
болсын. Онда (1) - жүйенің жалғыз шешімі бар және ол келесі формулалар арқылы табылады:
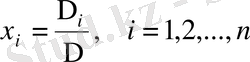 . (4)
. (4)
Мұндағы
 анықтауышынан оның
анықтауышынан оның
 - ші бағанын жүйенің бос мүшелер бағанымен ауыстыру арқылы алынатын анықтауыш.
- ші бағанын жүйенің бос мүшелер бағанымен ауыстыру арқылы алынатын анықтауыш.
2. САТЖ зерттеудің және оның шешімін табудың
Гаусс әдісі
Матрицалық әдіс пен Крамер ережесінің негізгі екі кемшілігі бар. Біріншіден, оларды нұқсансыз матрицалары бар теңдеулер жүйесіне ғана қолдануға болады; екіншіден, сандық теңдеулер жүйесін шешуде тиімсіз, өйткені ол әдістерді қолдану (Гаусс әдісіне қарағанда) n 2 есеге жуық есептеу амалдарын жасауды керек етеді, мысалы, n>10 болса, онда бұл әдістерді қолдану мүмкіндігі тіпті аз.
Элементар түрлендіру Гаусс әдісі кез келген тік бұрышты (квадрат қана емес) матрицалары бар теңдеулер жүйесін зерттеп және шешімін табуға (жүйенің шексіз көп шешімі бар жағдайда да) мүмкіндік береді.
Теңдеулер жүйесін зерттеу - оның үйлесімді (немесе үйлесімсіз) екенін, ал егер үйлесімді болса, онда жүйе шешімінің қанша болатынын анықтау.
Анықтама. САТЖ - нің кеңейтілген матрицасы деп жүйе матрицасының оң жағынан бос мүшелер бағанын тіркеп жазу арқылы алынған матрицаны айтады (тіркелген бос мүшелерді әдетте вертикаль сызықпен бөліп қояды) .
Мысалы, (1) - САТЖ матрицасы
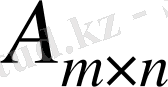 өлшемді болса, онда оның кеңейтілген матрицасы
өлшемді болса, онда оның кеңейтілген матрицасы
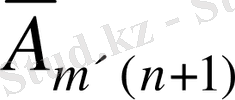 өлшемді болады:
өлшемді болады:
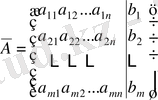 .
.
Олардың рангтерінің екі жағдайы:
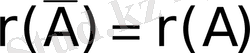 немесе
немесе
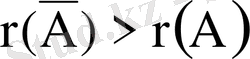 болуы мүмкін.
болуы мүмкін.
Келесі теорема теңдеулер жүйесін зерттеуге мүмкіндік береді.
Теорема (Кронекер-Капелли) . Сызықтық алгебралық теңдеулер жүйесінің матрицасы мен кеңейтілген матрицасының рангілері тең болса,
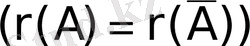 жүйе үйлесімді болады.
жүйе үйлесімді болады.
Енді теңдеулер жүйесін Гаусс схемасы бойынша зерттеу және шешу сұрақтарын қарастырайық.
Гаусс әдісімен
 және
және
 матрицаларының рангілерін анықтау үшін
матрицаларының рангілерін анықтау үшін
 - кеңейтілген матрицасын жазып алып (соңғы бос мүшелер бағанын өзгертпей) элементар түрлендірулер арқылы
- кеңейтілген матрицасын жазып алып (соңғы бос мүшелер бағанын өзгертпей) элементар түрлендірулер арқылы
 матрицасы трапеция тәріздес матрицаға келтіріледі. Егер бұл түрлендірулерде бағандар орын алмасқан болса, оларды өздеріне сәйкес белгісіздермен белгілеп отырады.
матрицасы трапеция тәріздес матрицаға келтіріледі. Егер бұл түрлендірулерде бағандар орын алмасқан болса, оларды өздеріне сәйкес белгісіздермен белгілеп отырады.
Трапеция тәріздес матрица рангісі туралы жоғарыда қарастырғанбыз. Сонымен
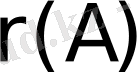 және
және
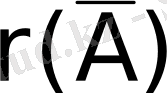 анықталды делік.
анықталды делік.
Келесі жағдайлар болуы мүмкін.
- . Бұл жағдайда Кронекер-Капелли теоремасы бойынша теңдеулер жүйесі үйлесімсіз.
2)
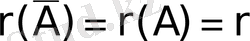 . Бұл жағдайда сол теорема бойынша теңдеулер жүйесі үйлесімді, сонымен бірге:
. Бұл жағдайда сол теорема бойынша теңдеулер жүйесі үйлесімді, сонымен бірге:
а) егер
 болса, яғни матрицалардың рангілері белгісіздер санына тең болса, онда жүйе шешімі жалғыз болады;
болса, яғни матрицалардың рангілері белгісіздер санына тең болса, онда жүйе шешімі жалғыз болады;
б) егер
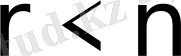 болса, онда теңдеулер жүйесінің
болса, онда теңдеулер жүйесінің
 параметрлеріне
параметрлеріне
 тәуелді шексіз көп шешімі болады.
тәуелді шексіз көп шешімі болады.
Ескерту. Қолданылған элементар түрлендірулер жүйенің шешімдер жиынын өзгертпейді, яғни жүйе бастапқы жүйеге мәндес болып қалады.
3. Біртекті сызықтық алгебралық теңдеулер жүйесі
Анықтама. Егер бос мүшелерінің барлығы нольге тең болса САТЖ - сі біртекті, ал бос мүшелер бағаны нөл емес САТЖ - сі біртекті емес деп аталады.
Біртекті САТЖ - сін келесі түрде жазуға болады.
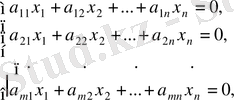
немесе матрицалық түрде
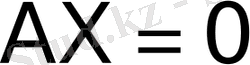 . Мұнда
. Мұнда
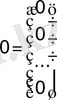 - нөл баған.
- нөл баған.
Біртекті жүйе әрқашанда үйлесімді, өйткені, оның тривиал деп аталатын
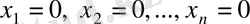 шешімі бар.
шешімі бар.
Матрицалық әдіс және Крамер ережесін біртекті жүйені шешуге қолданудың реті жоқ. Өйткені, егер
 болса, онда
болса, онда
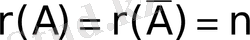
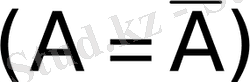 болады да жүйенің жалғыз тривиал шешімі бар; ал егер
болады да жүйенің жалғыз тривиал шешімі бар; ал егер
 болса, онда бұл әдістер жарамайды.
болса, онда бұл әдістер жарамайды.
Сондықтан, мұндай жағдайда біртекті жүйелерді шешудің Гаусс әдісін қолданамыз.
9, 10 дәріс
Тақырыбы: Вектор ұғымы. Векторларға сызықтық амалдар қолдану.
Анықтама.
Вектор деп бас нүктесі
 соңғы нүктесі
соңғы нүктесі
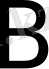 болатын өзіне өзін параллель жылжытуға болатын, бағытталған
болатын өзіне өзін параллель жылжытуға болатын, бағытталған
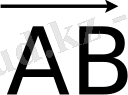 кесіндісін айтады.
кесіндісін айтады.
Сонымен, ұзындықтары тең
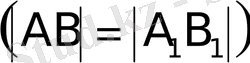 және бағыттары беттесетін екі
және бағыттары беттесетін екі
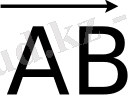 және
және
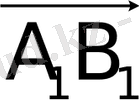 кесіндіні жалғыз ғана
кесіндіні жалғыз ғана
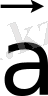 векторын анықтайды деп есептеп
векторын анықтайды деп есептеп

жазады (1-сурет) . Бұдан, вектор басы етіп кез келген нүктені алуға болатыны шығады.
 Егер
Егер
 мен
мен
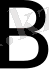 нүктелері беттессе, онда ол
нүктелері беттессе, онда ол
 арқылы белгіленеді де нөл вектор деп аталады.
арқылы белгіленеді де нөл вектор деп аталады.
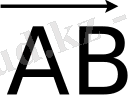 векторының модулі (ұзындығы)
векторының модулі (ұзындығы)
 деп
деп
 кесіндісінің ұзындығын айтады. Кейде
кесіндісінің ұзындығын айтады. Кейде
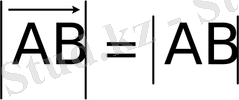 деп те жазыла береді. Нөл вектордың модулі нөлге тең
деп те жазыла береді. Нөл вектордың модулі нөлге тең
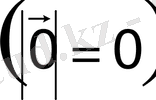 , оның бағыты болмайды.
, оның бағыты болмайды.
Бір түзуде немесе параллель түзулерде жататын векторлар коллинеар деп аталады. Нөл вектор кез келген векторға коллинеар деп есептеледі. Коллинеар векторларды
 арқылы белгілейді.
арқылы белгілейді.
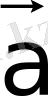 векторына коллинеар модулі
векторына коллинеар модулі
 тең, бағыты
тең, бағыты
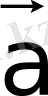 вектор бағытына қарама-қарсы бағытталған вектор
вектор бағытына қарама-қарсы бағытталған вектор
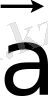 векторына қарама-қарсы вектор деп аталады да және
векторына қарама-қарсы вектор деп аталады да және
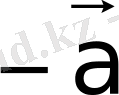 арқылы белгіленеді (1-сурет) .
арқылы белгіленеді (1-сурет) .
Анықтама.
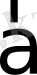 векторы мен
векторы мен
 санының көбейтіндісі
санының көбейтіндісі
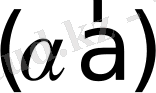 деп
деп
- модулітең;
- ;
- болса, - векторымен бағыттас, алболса, - векторына бағыты қарама-қарсывекторын айтады.
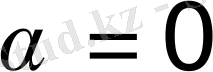 болса, онда
болса, онда
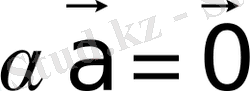 .
.
Анықтама.
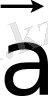 мен
мен
 векторларының қосындысы
векторларының қосындысы
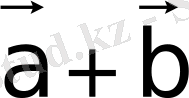 деп,
деп,
 векторының басы
векторының басы
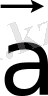 векторының ұшымен беттестірілген жағдайда,
векторының ұшымен беттестірілген жағдайда,
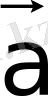 векторының басынан
векторының басынан
 векторының ұшына бағытталған
векторының ұшына бағытталған
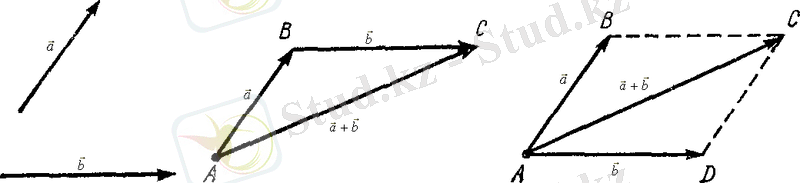
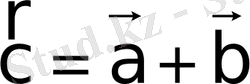 векторын айтады (2 - сурет) .
векторын айтады (2 - сурет) .
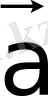 ,
,
 векторларының қосындысын табу үшін “үшбұрыш ережесін” пайдалануға болады: кез келген
векторларының қосындысын табу үшін “үшбұрыш ережесін” пайдалануға болады: кез келген
 нүктесіне
нүктесіне
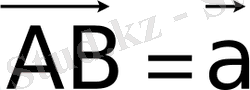 және
және
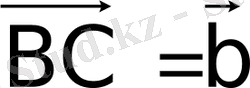 векторларын тұрғызса
векторларын тұрғызса
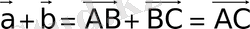 шығады; немесе “параллелограмм ережесін” пайдалануға болады;
шығады; немесе “параллелограмм ережесін” пайдалануға болады;
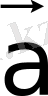 мен
мен
 векторларын ортақ
векторларын ортақ
 басына келтіреді де
басына келтіреді де
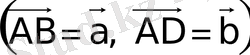 оларды қабырғалары етіп параллелограмм тұрғызады, оның
оларды қабырғалары етіп параллелограмм тұрғызады, оның
 нүктесінен шығатын
нүктесінен шығатын
 диоганалі
диоганалі
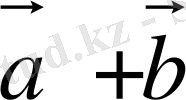 болады.
болады.
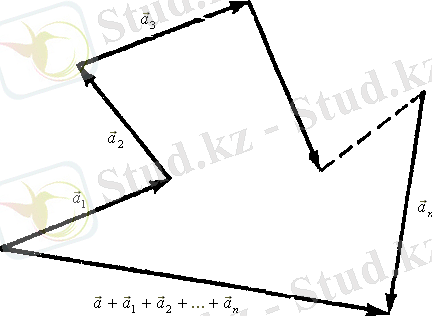
Бірнеше
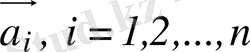 векторларды қосу үшін әрбір келесі
векторларды қосу үшін әрбір келесі
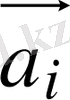 векторының басын алдыңғы
векторының басын алдыңғы
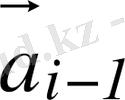 векторының ұшымен түйістіріп бірінші
векторының ұшымен түйістіріп бірінші
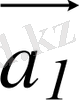 векторының басы мен соңғы
векторының басы мен соңғы
 векторының ұшын қосып
векторының ұшын қосып
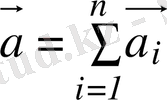 векторын тұрғызады (3 - сурет) .
векторын тұрғызады (3 - сурет) .
Бұл амалдар үшін келесі қасиеттер орындалады:
1
º
.
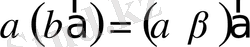 - ассоциативті (сандық көбейткіштерге қатысты) ;
- ассоциативті (сандық көбейткіштерге қатысты) ;
2
º
.
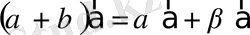 - дистрибутивті (сандарға қосуға қатысты) ;
- дистрибутивті (сандарға қосуға қатысты) ;
3
º
.
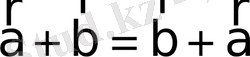 - коммутативті;
- коммутативті;
4
º
.
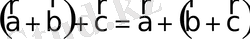 - ассоциативті;
- ассоциативті;
5
º
.
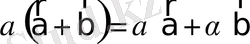 - дистрибутивті (векторларды қосуға қатысты) .
- дистрибутивті (векторларды қосуға қатысты) .
Анықтама.
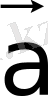 мен
мен
 векторларының айырымы
векторларының айырымы
 деп
деп
 векторымен қосындысы
векторымен қосындысы
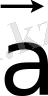 векторына тең болатындай
векторына тең болатындай
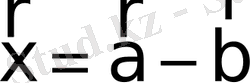 векторын айтады, яғни
векторын айтады, яғни
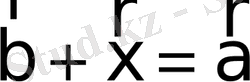 болса, онда
болса, онда
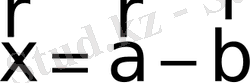 .
.
Бір нүктеден шығатын
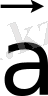 мен
мен
 векторының айырымын
векторының айырымын
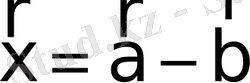 салу үшін
салу үшін
 векторының ұшын
векторының ұшын
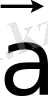 векторының ұшымен қосатын вектор тұрғызса болғаны немесе
векторының ұшымен қосатын вектор тұрғызса болғаны немесе
 (4 - сурет) .
(4 - сурет) .
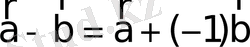 - теңдігінің дұрыстығын тексеру қиын емес.
- теңдігінің дұрыстығын тексеру қиын емес.
Анықтама.
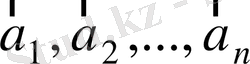 векторларының комбинациясы деп
векторларының комбинациясы деп
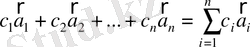 векторын айтады. Мұнда
векторын айтады. Мұнда
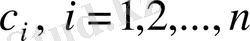 -сандар.
-сандар.
Анықтама.
Бір жазықтыққа параллель
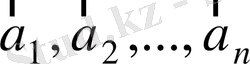 векторлары компланар деп аталады.
векторлары компланар деп аталады.
Векторлық кеңістік базисі. Вектор координаталары
Векторлық кеңістік деп кез келген сызықтық комбинациясы осы кеңістікте жататын векторлар жиынын айтады. Кез келген векторлық кеңістікте бірнеше векторларды таңдап алып осы кеңістіктің әрбір векторын, осы векторлардың бір мәнді сызықтық комбинациясы арқылы жазуға болады. Мұндай векторларды базистік деп атайды. Қысқа болу үшін түзу, жазықтық және кеңістік деп сәйкес векторлық түзу, векторлық жазықтық және векторлық кеңістіктерді атайтын боламыз.
Анықтама.
Түзудегі әрбір нөл емес
 векторы түзу базисі деп аталады. Кез келген коллинеар емес
векторы түзу базисі деп аталады. Кез келген коллинеар емес
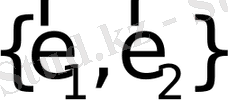 векторлар жұбы жазықтық базисі деп аталады. Кез келген компланар емес
векторлар жұбы жазықтық базисі деп аталады. Кез келген компланар емес
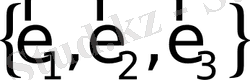 векторлар үштігі кеңістік базисі деп аталады.
векторлар үштігі кеңістік базисі деп аталады.
Базис туралы теорема.
Кеңістіктің әрбір
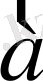 векторы
векторы
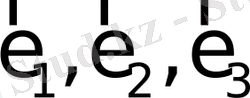 базистік векторлардың сызықтық комбинациясы болады және ол вектор үшін мұндай комбинация жалғыз ғана болады:
базистік векторлардың сызықтық комбинациясы болады және ол вектор үшін мұндай комбинация жалғыз ғана болады:
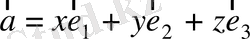 . (1)
. (1)
Анықтама.
Егер
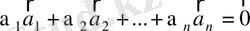 (*) теңдігінен
(*) теңдігінен
 шықса, онда
шықса, онда
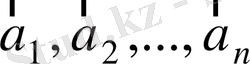 векторлар жүйесі сызықтық тәуелсіз деп аталады.
векторлар жүйесі сызықтық тәуелсіз деп аталады.
Егер (*) теңдігі орындалатындай барлығы бірдей бір мезгілде нөл емес
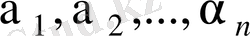 сандары бар болса, онда
сандары бар болса, онда
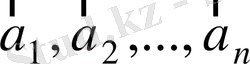 векторлар жүйесі сызықтық тәуелді деп аталады. Анық болу үшін
векторлар жүйесі сызықтық тәуелді деп аталады. Анық болу үшін
 деп алсақ, онда
деп алсақ, онда
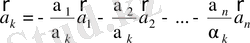 .
.
Сонымен, егер
 векторлар жүйесі сызықтық тәуелді болса, онда олардың бірі, қалған векторлардың сызықтық комбинациясы болады.
векторлар жүйесі сызықтық тәуелді болса, онда олардың бірі, қалған векторлардың сызықтық комбинациясы болады.
Ескерту. Базистік векторлар туралы теорема дәлелдемесінен: базистік векторлар жүйесі сызықтық тәуелсіз болатынын көреміз.
(1) теңдікті
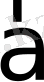 векторының
векторының
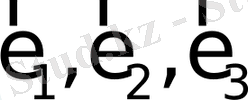 базисі бойынша жіктелуі деп атайды да,
базисі бойынша жіктелуі деп атайды да,
 - сандарын
- сандарын
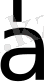 векторының
векторының
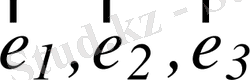 базисіндегі координаталары деп атайды және
базисіндегі координаталары деп атайды және
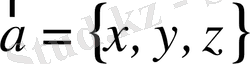 деп жазады.
деп жазады.
1-теорема. Векторларды қосқанда олардың сәйкес координаталары қосылады, ол векторды санға көбейткенде оның барлық координаталары осы санға көбейтіледі.
2-теорема.
Екі вектор тең болуы үшін олардың сәйкес координаталарының тең болуы қажетті және жеткілікті, яғни
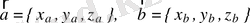 болса, онда
болса, онда
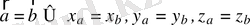 .
.
3-теорема.
(Координаталы векторлардың коллинеарлық белгісі)
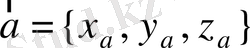 және
және
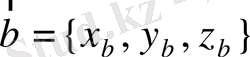
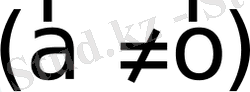 берілсін. Онда
берілсін. Онда
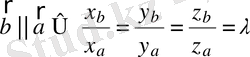 ,
,
яғни
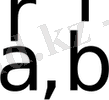 векторлары коллинеар болуы үшін олардың сәйкес координаталарының пропорционал болуы қажетті және жеткілікті.
векторлары коллинеар болуы үшін олардың сәйкес координаталарының пропорционал болуы қажетті және жеткілікті.
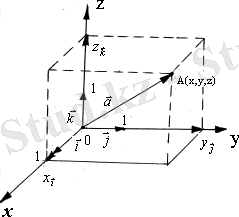 Кеңістікте
Кеңістікте
 тік бұрышты декарт координаталар жүйесі берілсін. Бұл жүйемен байланыста болатын, сәйкес ОХ, ОY, OZ өстерінің бойында орналасқан
тік бұрышты декарт координаталар жүйесі берілсін. Бұл жүйемен байланыста болатын, сәйкес ОХ, ОY, OZ өстерінің бойында орналасқан
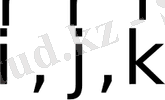 бірлік векторлары
бірлік векторлары
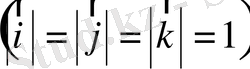 кеңістік базисін құрайды (5 - сурет) . Оларды сәйкес ОХ, ОY, OZ өстерінің орттары деп атайды.
кеңістік базисін құрайды (5 - сурет) . Оларды сәйкес ОХ, ОY, OZ өстерінің орттары деп атайды.
Кеңістіктің кез келген
 нүктесін алайық.
нүктесін алайық.
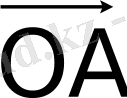 векторы (басы координаталар бас нүктесінде, ұшы
векторы (басы координаталар бас нүктесінде, ұшы
 нүктесі болатын)
нүктесі болатын)
 - нүктесінің радиус-векторы деп аталады. Егер
- нүктесінің радиус-векторы деп аталады. Егер
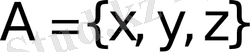 болса, онда
болса, онда
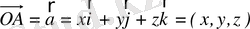 теңдігін жаза аламыз. Шынында да,
теңдігін жаза аламыз. Шынында да,
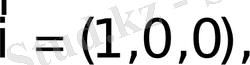

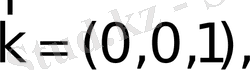 болғандықтан
болғандықтан
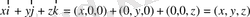 .
.
Тік бұрышты координаталар жүйесінде
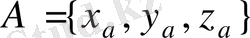 ,
,
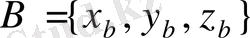 нүктелері берілсе, онда
нүктелері берілсе, онда
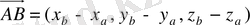 .
.
Расында да,
 .
.
Кейде
 базисіндегі вектор координаталарын проекция ретінде жазу ыңғайлы.
базисіндегі вектор координаталарын проекция ретінде жазу ыңғайлы.
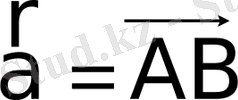 векторының бағытталған
векторының бағытталған
 түзуіне проекциясы
түзуіне проекциясы
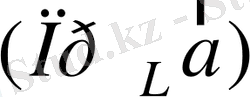 деп
деп
 векторын айтады, мұндағы
векторын айтады, мұндағы
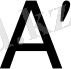 ,
,
 нүктелері
нүктелері
 мен
мен
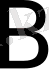 нүктелерінің
нүктелерінің
 түзуіне проекциялары (6-сурет) .
түзуіне проекциялары (6-сурет) .
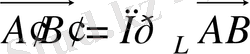 .
.
 - векторының екі түрлі ғана бағыты бар: егер
- векторының екі түрлі ғана бағыты бар: егер
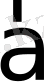 мен
мен
 -нің арасындағы бұрыш сүйір, яғни
-нің арасындағы бұрыш сүйір, яғни
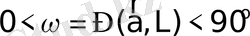 болса, онда оның бағыты
болса, онда оның бағыты
 түзуінің бағытымен беттеседі де, ал доғал,
түзуінің бағытымен беттеседі де, ал доғал,
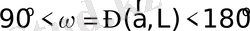
болса, онда
 - векторы
- векторы
 түзуінің бағытына қарама-қарсы болады. Сондықтан,
түзуінің бағытына қарама-қарсы болады. Сондықтан,
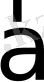 векторының бағытталған
векторының бағытталған
 - түзуіне проекциясын келесі түрде анықтайды.
- түзуіне проекциясын келесі түрде анықтайды.
Анықтама.
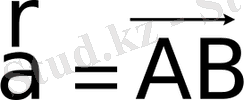 векторының
векторының
 - бағытталған түзуге проекциясы деп
- бағытталған түзуге проекциясы деп
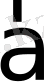 вектор ұзындығының
вектор ұзындығының
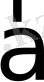 векторы мен
векторы мен
 - түзуінің бағыты арасындағы
- түзуінің бағыты арасындағы
 бұрышының косинусына көбейтіндісін айтады:
бұрышының косинусына көбейтіндісін айтады:
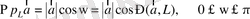 . (1)
. (1)
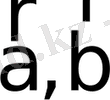 векторларының берілген бағытқа проекциялары келесі қасиеттерге ие:
векторларының берілген бағытқа проекциялары келесі қасиеттерге ие:
1
º
.
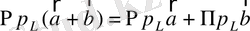 ; (2)
; (2)
2
º
.
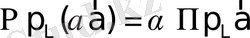 (3)
(3)
3
º.
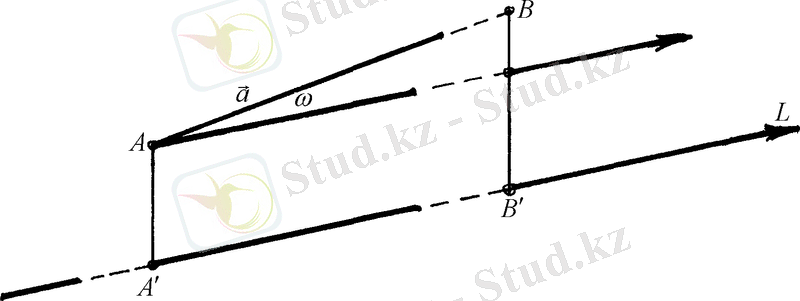
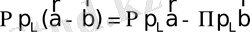 (4)
(4)
аламыз.
11, 12 дәріс
Тақырыбы: Векторлардың скаляр көбейтіндісі
Анықтама.
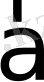 мен
мен
 векторларының скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы
векторларының скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы
 бұрышының косинусының көбейтіндісіне тең
бұрышының косинусының көбейтіндісіне тең
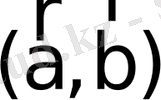 (немесе
(немесе
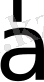
 ) санын айтады:
) санын айтады:
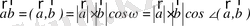 . (5)
. (5)
(1) - теңдікті ескеріп (5) - теңдікті келесі түрде де жаза аламыз:
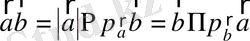 . (6)
. (6)
Скаляр көбейтіндінің арифметикалық қасиеттері:
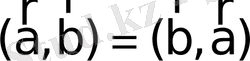 , (7)
, (7)
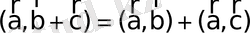 , (8)
, (8)
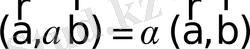 . (9)
. (9)
Нөл емес
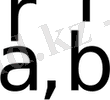 векторлары үшін:
векторлары үшін:
- (векторлары ортогональ) ;
- - сүйір бұрыш;
- - доғал бұрыш.
Кез келген
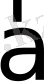 векторы үшін
векторы үшін
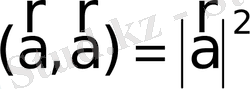 . (10)
. (10)
Тік бұрышты декарт координаталар жүйесінің координаттық орттары
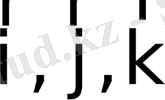 үшін
үшін
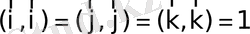 , (11)
, (11)
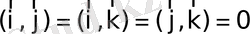 . (12)
. (12)
Егер
 базисінде
базисінде
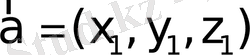 ,
,
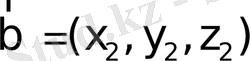 векторлары берілсе, онда
векторлары берілсе, онда
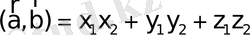 . (13)
. (13)
Дербес жағдайда
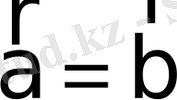 болса, онда (10) және (13) теңдіктерден
болса, онда (10) және (13) теңдіктерден
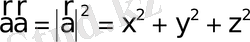 ,
,
бұдан
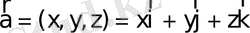 векторының ұзындығын аламыз:
векторының ұзындығын аламыз:
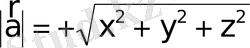 . (14)
. (14)
Егер
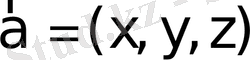 ,
,
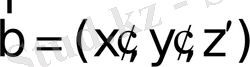 берілсе, онда (14) теңдіктен
берілсе, онда (14) теңдіктен
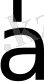 мен
мен
 нүктелерінің ара қашықтығының формуласы шығады
нүктелерінің ара қашықтығының формуласы шығады
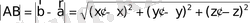 (15)
(15)
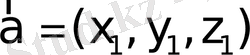 және
және
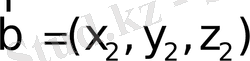 векторларының арасындағы
векторларының арасындағы
 бұрышы
бұрышы
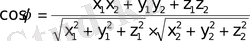 (16)
(16)
тең.
(16) - теңдіктен
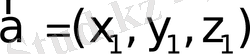 және
және
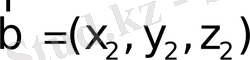 векторларының ортогональдық
векторларының ортогональдық
 белгісін алуға болады:
белгісін алуға болады:
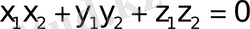 (17)
(17)
Скаляр көбейтіндінің механикалық мағынасы.
 күшінің
күшінің
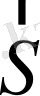 векторына скаляр көбейтіндісі, материалдық нүктенің осы күш әсерінен
векторына скаляр көбейтіндісі, материалдық нүктенің осы күш әсерінен
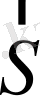 векторы бойымен қозғалғандағы жұмысқа тең, яғни
векторы бойымен қозғалғандағы жұмысқа тең, яғни
 .
.
Скаляр көбейтіндінің геометриялық қасиеттері:
1. Нөлдік емес
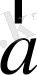 және
және
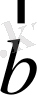 екі вектордың скаляр көбейтіндісі нөлге тең болғанда, тек сонда ғана олар өзара перпендикулр болады:
екі вектордың скаляр көбейтіндісі нөлге тең болғанда, тек сонда ғана олар өзара перпендикулр болады:
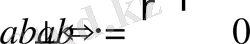 .
.
2. Нөлдік емес
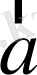 және
және
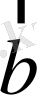 екі вектордың скаляр көбейтіндісі оң (теріс), яғни
екі вектордың скаляр көбейтіндісі оң (теріс), яғни
 болғанда, тек сонда ғана олар өзара сүйір (доғал) бұрыштар жасайды.
болғанда, тек сонда ғана олар өзара сүйір (доғал) бұрыштар жасайды.
13, 14, 15- дәріс
Тақырыбы: Векторлардың векторлық және аралас көбейтіндісі
Анықтама.
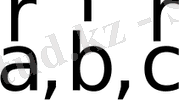 - бастары ортақ бір
- бастары ортақ бір
 нүктесіне келтірілген, компланар емес, реттелген векторлар үштігі болып
нүктесіне келтірілген, компланар емес, реттелген векторлар үштігі болып
 вектор ұшынан қарағанда
вектор ұшынан қарағанда
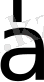 - нан
- нан
 - на жақын тұспен бұрылу сағат тілінің бағытына қарама-қарсы бағытта болса, онда
- на жақын тұспен бұрылу сағат тілінің бағытына қарама-қарсы бағытта болса, онда
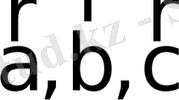 - оң үштік векторлар, сағат тілі бағытымен бірдей болса
- оң үштік векторлар, сағат тілі бағытымен бірдей болса
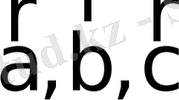 - теріс үштік векторлар деп аталады.
- теріс үштік векторлар деп аталады.
Анықтама.
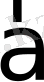 мен
мен
 векторларының векторлық көбейтіндісі деп келесі үш шартты қанағаттандыратын
векторларының векторлық көбейтіндісі деп келесі үш шартты қанағаттандыратын
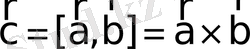 векторын айтады:
векторын айтады:
- векторының модульдері мен осы екі вектор арасындағы бұрыштың синусының көбейтіндісіне тең:
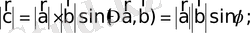
- әрбіржәневекторларына ортогональ, яғни олменарқылы өтетін жазықтыққа перпендикуляр;
- векторлары реттелген оң үштік векторлар.
Мысалы
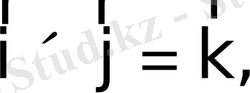
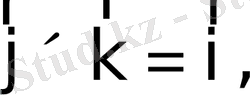
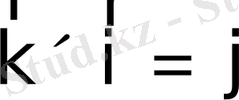 (1)
(1)
Векторлы көбейтінді үшін негізгі келесі үш қасиет орындалады:
1
0
.
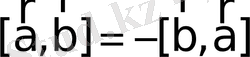 - антикоммутативтік, яғни векторлық көбейтінді ауыстырымдылық заңына бағынбайды;
- антикоммутативтік, яғни векторлық көбейтінді ауыстырымдылық заңына бағынбайды;
2
0
.
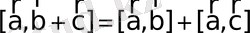 - дистрибутивтік (векторларды қосуға қатысты) ;
- дистрибутивтік (векторларды қосуға қатысты) ;
3
0
.
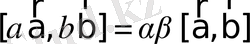 - ассоциативтік (санға көбейтуге қатысты) ;
- ассоциативтік (санға көбейтуге қатысты) ;
Сонымен бірге келесі қасиеттер де орындалады:
а)
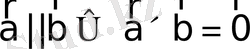 , яғни
, яғни
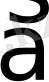 мен
мен
 векторларының векторлық көбейтіндісі нөл вектор болса және тек сонда ғана олар коллинеар болады;
векторларының векторлық көбейтіндісі нөл вектор болса және тек сонда ғана олар коллинеар болады;
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz