Координаталар әдісі: координаттық жүйелер, түрлендірулер және еселі интегралдар


Ф-ОБ-001/035
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті
«Математика» кафедрасы
К У Р С Т Ы Қ Ж Ұ М Ы С
Тақырыбы: Координаталар әдісі.
Орындаған: Сулейменова Айгерім
Ғылыми жетекші: Назарова Күлзина
Тобы: ЖМА-011
Түркістан 2012
Мазмұны
Кіріспе . . .
I-Тарау: Координаталар жүйесі
1. 1 Координаталық өс . . .
1. 2 Жазықтықтағы координаталар жүйесі . . .
1. 3 Басқа координаталар жүйелері туралы мәліметтер . . .
II-Тарау: Декарттық тікбұрышты координаталарды түрлендіру.
2. 1 Жазықтықтағы координаталар өстерін параллель көшіру . . .
2. 2 Жазықтықтағы координаталар өстерін бұру . . .
2. 3 Кеңістіктегі координаталар өстерін параллель көшіру . . .
2. 4 Кеңістіктегі координаталар өстерін бұру . . .
III - тарау. Еселі интегралдар . . .
3. 1 Еселі интегралдар . . .
3. 2 Айнымалыларды ауыстыру . . .
Пайдаланылған әдебиеттер тізімі
Қорытынды
Кіріспе
Координаттар (лат. co - бірге және ordіnatus - тәртіптелген, анықталған) - жазықтықтағы, кез келген беттегі не кеңістіктегі нүктенің орнын анықтайтын сандар. Ғылымға, ең әуелі, аспан сферасындағы не Жер шары бетіндегі нүктенің орнын (ендік пен бойлық) анықтайтын астрономиялық және географиялық координаттар енді. 17 ғасырда Рене Декарт(31-наурыз 1596 жылы- 11- ақпан 1650жылы) координаттар әдісі арқылы геометрия мен математикалық анализдің арасындағы өзекті байланысты ашты. Р. Декарт(фр. Rene Descartes) 31-наурызда Лаэ (Турень провинциясы) дүниеге келген. Декарт- француз математигі, философ, физик және физиолог, аналитикалық геометрия мен алгебралық символдарды құрастырушы, философияда күмәндану теориясының авторы, рефлексологияның бастаушысы, математика, физика, геометрия, философия және тағы басқа ғылым салаларына көп үлесін қосқан әйгілі математик. Ғылыми еңбектері де көп. Аналитикалық геометрияны құрастыру оған қисықтар мен денелердің геометриялық қасиеттерін алгебра тіліне аударуға мүмкіндік берді, яғни қисықтар теңдеуі мен біршама координаттар жүйесіне талдау жасады. Бұл аударма біраз жеткіліксіздіктерге толы болды, енді оның мұқият геометриялық қасиеттерін анықтап, координатаға тәуелді емес инварианттарды табу керек еді. Бірақ жаңа әдіспен ұлы Декарт қана ескі және жаңа белгісіздерді зерттей білді. Декарт сондай-ақ алгебралық, механикалық және трансценденттік функцияларға өз үлесін қосты. Механикада, математикада, физикада, тағы басқа салаларда сфералық координаттар (θ, ϕ, r, ), цилиндрлік координаттар ( z, ϕ, ρ), эллипсоидтық координаттар жиі қолданылады. Кеңістіктегі біртекті координаттар жазықтықтағы координаттар сияқты енгізіледі.
Координаттар әдісінің мәні - жазықтықта орналасқан кез келген М(х, у) нүктесін декарттық координаттар жүйесі арқылы анықтауға болатындығында, х және у шамалары Оху жүйесіндегі М нүктесінің декарттық тік бұрышты координаттары (не қысқаша тік бұрышты координаттар) деп аталады. Осыған сәйкес оларды М нүктесінің абсциссасы (х) және ординатасы (у) деп атайды.
1. 1 Координаталық өс
Кез келген түзу берілсін. Түзу бойынан кез келген О нүктесін алып және бір бағытын оң деп есептейік. Алынған жүйені өс деп атаймыз.
О О
О
Мұны ең алғаш рет Декарт енгізген болатын. Өс бойынан А және В нүктелерін алайық.
Егер АВ кесіндісінің басы мен соңы белгілі болса, онда оны бағытталған кесінді деп аталады. В басы А аяғы ВА кез келген бағыталған кесіндіге белгілі бір характеристикалық сан сәйкес келеді. Оны бағытталған кесіндінің шамасы деп аталады. Және ВА - сызықшасыз (векторсыз) . Ол ұзындықты + таңбамен алғанға тең. Егер оң бағытталса ұзындық - теріс таңбамен алғанға тең. Егер оң бағытқа кері бағыттас болса.
ВА = - АВ АВ=
AB = - BA (1. 1)
Теорема 1. Өс бойында А, В, С нүктелері қалай орналасса да
АВ +ВС = АС (1. 2)
теңдікті аналитикалық геометрияның негізгі тепе-теңдігі деп аталады.
АD + DF = AF.
Дәлелдеу В С А ВС + СА = BA
BC - AC = - AB
AB + BC = AC
2. C A B 3. A C B
CA +AB = CB
- AC + AB = - BC AC + CB = AB
AB + BC = AC AC - BC =AB
l AC = AB + BC
О
Өс бойынан бірлік өлшем масштаб алайық. Алынған жүйені координаталық өс деп атаймыз. Координаталық өс бойынан кез келген М нүктесі берілсін. ОМ шамасын М нүктесінің координатасы деп аталады және келесі символмен белгілейміз. : М(x)
x = OM О l M
Теорема 2. М 1 (x 1 ) және М 2 (x 2 ) нүктелері берілсін. Онда
М 1 М 2 = x 1 - x 2 (1. 3)
Кез келген 2 нүкте шамасын анықтаймыз.
Дәлелдеу: ОМ 1 + М 1 М 2 = ОМ 2
М 1 М 2 = ОМ 2 - ОМ 1
М 1 М 2 = x 2 - x 1
М 1 М 2 = x 2 - x 1 = ОМ 2 - ОМ 1
Теорема 3. М 1 (x 1 ) және М 2 (x 2 ) нүктелері берілсін.
d = x 2 - x 1 (1. 4)
Ұзындық әрдайым оң шама.
1. 2 Жазықтықтағы координаталар жүйесі
Бірдей өлшемді екі координаталық өс өзара тік бұрыш жасап қиылысады. Олардың ортақ қиылысу нүктесін О деп белгілейік. Алынған жүйені жазықтықтағы тік Декарттық координаталар жүйесі деп аталады. 1- ші өсті х 2 - ші өсті у әріпімен белгілейік. 1 -ші өсті ох өсіне абсцисса өсі деп атаймыз. 2 - ші өсті оу не ордината өсі деп аталады. Жазықтықтағы координаталар тік Декартық жүйесі жазықтықты 4 бөлікке бөледі. Оларды ширек деп атайды. I x <0 y>0 III x<0 y <0
II I II x <0 y>0 IV x >0 y<0
X
III IV
O(0; 0) М у М 0
O l M x X
Жазықтықта кез келген М нүктесі берілсін. Сәйкес координаталық өстерге проекциялар түсірейік. Оның ОХ қиылысуын нүктесін М х , OY өсімен қиылысу нүктесін ОY- М y белгілейміз. Сонда OМ х , OM y шамаларын М нүктесінінің координаталары деп аталады: М (х, у) Мұнда Х = OМ х Y = OM y
M М у Y OМ х = - 4 M нүктесінің координатасы
М x 0 l X OМ у = 5, 5 M( -4 ; 5, 5)
1. 3 Басқа координаталар жүйелері туралы мәліметтер
Декарттық координаталар жүйесі реттелген нақты сандар арқылы жазықтықтағы немесе кеңістіктегі нүктелердің орнын анықтаудағы жалғыз ғана тәсіл емес. Бұл мақсатта басқа да координаталар жүйесін жиі қолданады.
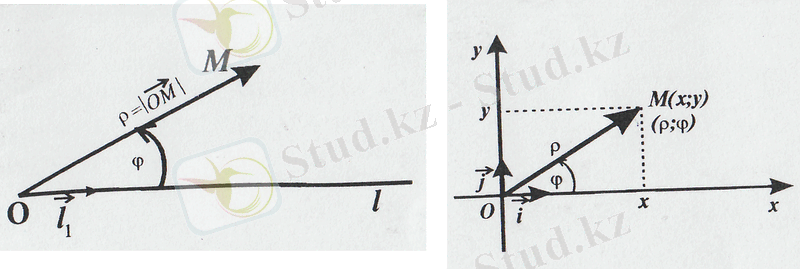
Жазықтықтағы полярлық координаталар жүйесі.
Жазықтықта О нүктесі және осы нүкте бастапқы нүктесі болатын
l
сәулесін аламыз.
l
сәулесінің бағыты
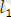
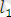 бірлік векторының бағытымен анықталсын. О нүктесін полярлық полюс, ал
l
сәулесін полярлық өс деп атайды. Жазықтықтағы м нүктесінің орны екі нақты санмен, атап айтқанда, ρ=
бірлік векторының бағытымен анықталсын. О нүктесін полярлық полюс, ал
l
сәулесін полярлық өс деп атайды. Жазықтықтағы м нүктесінің орны екі нақты санмен, атап айтқанда, ρ=
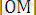
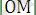 санымен және сағат тілінің айналу бағытына қарсы бағытпен өлшенетін полярлық
l
өсі мен
санымен және сағат тілінің айналу бағытына қарсы бағытпен өлшенетін полярлық
l
өсі мен
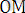
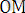 векторының арасындағы φ бұрышымен толықтай анықталады (1- сурет) .
векторының арасындағы φ бұрышымен толықтай анықталады (1- сурет) .
ρ≥0 cаны полярлық радиус, ал φ саны полярлық бұрыш деп аталады. Бұл сандар М нүктесінің полярлық координаталары деп аталып м әріпінен кейін ретпен жақша ішінде жазылады, яғни M(ρ, φ) . Полярлық полюс нүктесінде ρ=0 болады да, ал φ бұрышы бір мәнді анықталмай, [0; 2π) аралығының кез келген мәнін қабылдайды. Жазықтықтың барлық басқа нүктелері үшін ρ>0 болады да, ал φϵ[0; 2π) . ρ>0 болатын және 0≤φ<2π теңсіздігі қанағаттанатын кез келген (ρ, φ) сандар полярлық координаталары болатын жазықтықта жалғыз ғана нүкте бар. Енді жазықтықтағы бір ғана м нүктесінің декарттық және полярлық координаталарының арасындағы байланысты табайық. Жазықтықта декарттық тік бұрышты Оху координаталар жүйесі берілсін. Координаталар бас нүктесін полярлық полюс, ал абсцисса өсін полярлық өс деп алайық (2 - сурет) .
Сонда М нүктесінің декарттық (х, у) координаталары, оның полярлық (ρ, φ) координаталары арқылы мына формулалармен өрнектеледі.
x= ρcosφ, y= ρsinφ (1. 5)
Егер ρ≠0 болса, онда (14) формулаларды пайдаланып, керісінше, м нүктесінің полярлық (ρ, φ) координаталарын, оның декарттық (х, у) координаталары арқылы өрнектеуге болады. Шынында да,
x 2 + y 2 =ρ 2 (cos 2 φ + sin 2 φ) =ρ 2 ,
немесе
ρ =
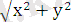
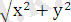 ; cos φ =
; cos φ =

 =
=
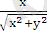
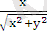 ; (1. 6)
; (1. 6)
sin φ =

 =
=
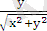
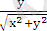 .
.
1- сурет 2- сурет
Кеңістіктегі цилиндрлік координаталар жүйесі.
Кеңістікте О нүктесін белгілеп алып және осы нүкте арқылы (α) жазықтығын жүргіземіз. (α) жазықтығында жатқан басы О нүктесінде орналасып, үстінде белгілі бағыт көрсетілген сәулені полярлық өс деп аламыз. (α) жазықтығына перпендикуляр

 векторын алып,
векторын алып,

 векторының соңғы нүктесінен қарағанда . (α) жазықтығы о нүктесін айнала сағат тілінің бағытына қарсы бағытта бұрылады деп санаймыз.
векторының соңғы нүктесінен қарағанда . (α) жазықтығы о нүктесін айнала сағат тілінің бағытына қарсы бағытта бұрылады деп санаймыз.
Кеңістікте м нүктесі берілсін. Осы нүктеде (α) жазықтығына MM 1 перпендикуляр жүргіземіз.
М нүктесінің кеңістіктегі цилиндрлік координаталарын (ρ, φ, 𝓏) арқылы белгілейміз. Мұндағы ρ, φ сандары жазықтықтағы о полюсі мен
l
полярлық өсіндегі M
1
нүктесінің полярлық координаталары, ал 𝓏 саны
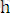
 векторына коллинеар MM
1
векторының координатасы (3 а - сурет) .
векторына коллинеар MM
1
векторының координатасы (3 а - сурет) .
Егер абсцисса өсінің оң жартысы полярлық
l
өсімен дәл келіп, ал
 вектoры аппликата өсінің орты болатын болса, онда кеңістікте декарттық тік бұрышты координаталар жүйесін енгізсек, м нүктесінің декарттық координаталары (х, у, 𝓏) координаталары, оның цилиндрлік координаталары арқылы былай өрнектеледі:
вектoры аппликата өсінің орты болатын болса, онда кеңістікте декарттық тік бұрышты координаталар жүйесін енгізсек, м нүктесінің декарттық координаталары (х, у, 𝓏) координаталары, оның цилиндрлік координаталары арқылы былай өрнектеледі:
x= ρ ∙ cos φ, y = ρ ∙ sin φ, 𝓏 = 𝓏 (1. 7)
Сфералық координаталар жүйесі. Жоғарыдағы айтылғандарға ұқсас, (α) жазықтығында жатқан O нүктесін алып, Oх оң жарты өсін сызамыз және оны полярлық өс деп санаймыз. κ⊥(α) болсын, мұндағы (α) жазықтығы Oху координаталар жазықтығымен беттесіп кетеді де κ векторы аппликата өсі O𝓏 өсімен бағыттас болады. Кеңістіктен М нүктесін алып, векторының модулін r санымен белгілейміз. O𝓏 өсінің ОМ түзуімен жасайтын бұрыш - θ болсын (3 б - сурет) .
М нүктесінің сфералық координаталарын (r, φ, θ) нақты сандар үштігімен белгілеп, олардың (х; у; 𝓏) декарттық координаталарын (r, φ, θ) үштігі арқылы өрнектейміз.
Ол үшін OMM 1 бұрышының θ-ге тең болатынын ескеріп, тік бұрышты OMM 1 үшбұрышынан
ρ= r ∙ sin θ, 𝓏 = r∙ cos θ (1. 8)
теңдіктерін тауып аламыз. OАM 1 тікбұрышты үшбұрышынан
x= ρ ∙ cos φ, y = ρ ∙ sin φ (1. 9)
формулалары шығады.
(1. 8) және (1. 9) формулаларды ескеріп, кеңістіктегі м нүктесінің декарттық (х, у, 𝓏) координаталары мен оның сфералық (r, φ, θ) координаталарының бізге қажет ара байланысын мына формулалар арқылы өрнектейміз:
x= r ∙ cos φ∙ sinθ, y = r ∙ sin φsinθ, 𝓏 = r∙ cos θ (1. 10) .
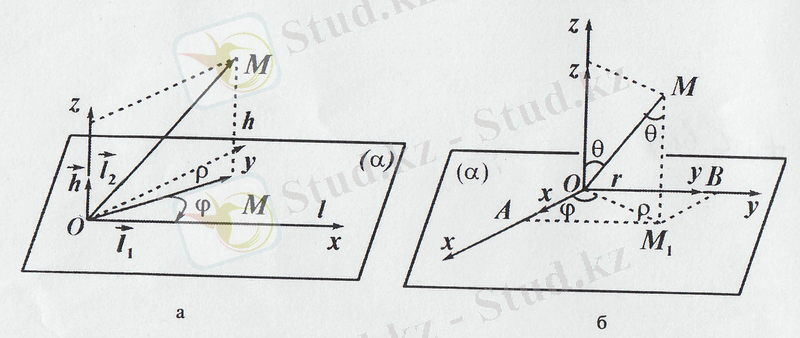
3 - сурет
2. 1 Жазықтықтағы координаталар өстерін параллель көшіру
Жазықтықтағы декарттық тік бұрышты екі координаталар жүйесі Оху және О ׳ х ׳ у ׳ берілсін. Егер О ׳ х ׳ және О ׳ у ׳ өстері сәйкес Ох және Оу өсіне параллель болса, онда Ох ׳ у ׳ жүйесі Оху жүйесінен параллель көшіру нәтижесінде алынған дейді (4 - сурет) . М нүктесі жазықтықтың кез келген нүктесі дейік және (х, у) пен (х ׳ , у') оның сәйкес Оху және О'х'у' жүйелеріндегі координаталары болсын. О' нүктесінің Оху координаталар жүйесіндегі координаталарын (a, b) арқылы белгілейік.
Сонда векторларды қосудың үшбұрыш ережесі бойынша
 =
=
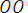
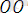 +
+
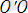
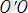 +
+
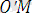
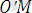 (1. 11)
(1. 11)
болады.
Бұл векторлар сәйкес нүктелердің радиус-векторлары болғандықтан, олардың координаталары мынадай болады:
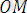
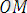 = (х, у),
= (х, у),
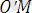
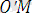 = (х
׳
, у'),
= (х
׳
, у'),
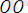
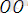 = (a, b) (1. 12)
= (a, b) (1. 12)
Енді (11) және (12) формулалардан
х=x' + a, y=y' + b (1. 13)
теңдіктері шығады.
Сонымен, (1. 13) формулалары бірінен-бірі параллель көшіру арқылы алынған координаталар жүйелеріндегі кез келген М нүктесінің сәйкес координаталары арасындағы байланысты көрсетеді.
Мысал. 9х 2 + 4у 2 - 18х + 8у - 23 = 0 теңдеуі берілсін. Координаталар өстерін параллель көшіру арқылы берілген теңдеуді белгісіздердің бірінші дәрежесі болмайтын теңдеулерге түрлендір.
9х 2 + 4у 2 - 18х + 8у - 23 =9(x ׳ + a ) 2 + 4(y ׳ + b) 2 - 18(x ׳ + a) + 8(y ׳ + b) - 23 =0
немесе,
9х ׳ 2 + 4у ׳ 2 +(18a - 18 ) x ׳ + (8b + 8 ) y ׳ + 9a 2 +4b 2 - 18a + 8b - 23 = 0.
Есептің шарты бойынша
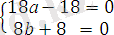
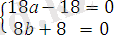
Бұдан a = 1, b = - 1, яғни O ׳ (1, -1) - координатлар жүйесінің жаңа бас нүктесі.
Енді теңдеудің бос мүшесін табамыз.
(9a 2 +4b 2 - 18a + 8b - 23) =9+4-18-8-23=-36
Сонда түрлендірілген теңдеу мына түрде жазылады:
9х ׳ 2 +4у ׳ 2 -36=0 ⇒9х ׳ 2 +4у ׳ 2 =36.
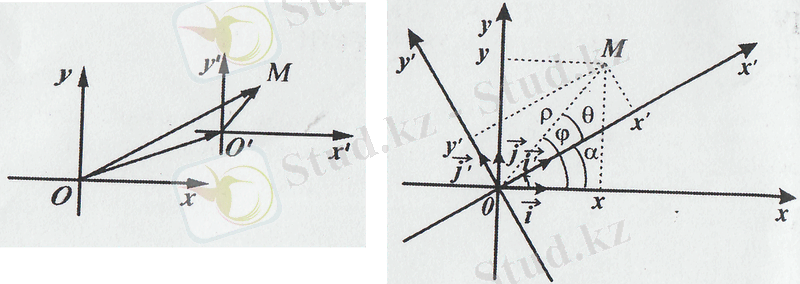 4 - сурет 5 - сурет
4 - сурет 5 - сурет
2. 2 Жазықтықтағы координаталар өстерін бұру
Бас нүктелері ортақ бір нүктеде жатқан Оху және Ох ׳ у ׳ және декарттық тік бұрышты координаталар жүйелерін аламыз. Ох өсін Ох ׳ өсімен беттестіру үшін оны сағат тілінің айналу бағытына қарсы бағытта бұру бұрышын α арқылы белгілейміз (5 - сурет) .
Жазықтықта полюсі О нүктесінде жатқан, полярлық өстері сәкес оң бағыттағы Ох және Ох ׳ жарты өстерімен беттескен екі полярлық координаталар жүйесін енгіземіз. М - жазықтықтың кез келген нүктесі болсын және оның бірінші полярлық координаталар жүйесіндегі координаталарын (ρ, φ) арқылы белгілейік.
Сонда
x=
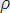
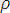 ∙ cos𝜑; y=ρ ∙ sin𝜑. (1. 14)
∙ cos𝜑; y=ρ ∙ sin𝜑. (1. 14)
Осылайша, (r, θ) М нүктесінің екінші полярлық жүйедегі координаталары дейік, сонда
x
׳
=
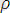
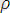 ∙ cosθ; y=ρ ∙ sinθ. (1. 15)
∙ cosθ; y=ρ ∙ sinθ. (1. 15)
Ал
𝜑 + 2

 = α + θ (1. 16)
= α + θ (1. 16)
болсын. Мұндағы κ = 0 немесе 1-ге тең. (1. 14), (1. 15), (1. 16) формулаларды пайдаланып, мынаны табамыз:
x=ρcos 𝜑 = ρcos (𝜑+2πκ) = ρcos(α+θ) = ρcosαcosθ - ρsinαsinθ=x ׳ cosα - y sin α;
x=ρsin 𝜑 = ρsin (𝜑+2πκ) = ρsin(α+θ) = ρsinαsinθ - ρcosαsinθ=x ׳ sin α - y cos α.
Сонымен, бас нүктені айнала координаталар өсінен бұрғандағы координаталардың түрлену формулалары мына түрде жазылады.
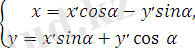
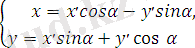 (1. 16
׳
)
(1. 16
׳
)
Жалпы жағдайда, бас нүктелері әр басқа нүктелерде орналасқан және сәйкес координаталар өстері параллель болмайтын Оху және Ox
׳
y
׳
жүйелерін беттестіру үшін, алдымен Охy жүйесін
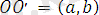
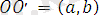 векторына параллель көшіріп сосын оны α бұрышына бұрсақ болғаны. Сонда (1. 13) және (1. 14) формулаларынан жалпы мына формуланы аламыз:
векторына параллель көшіріп сосын оны α бұрышына бұрсақ болғаны. Сонда (1. 13) және (1. 14) формулаларынан жалпы мына формуланы аламыз:
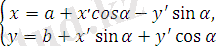
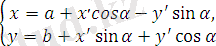 (1. 16*)
(1. 16*)
Мысал. Тік бұрышты координаталар жүйесін 45°-қа бұрғанда
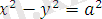
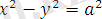 теңдеуі қандай түрге түрленеді?
теңдеуі қандай түрге түрленеді?
Бұл есепті шығару үшін (1. 16) - формулаларды пайдаланамыз. Мұндағы α=45°.
x=
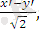
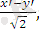 y=
y=
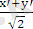
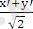
Сондықтан,
a
2
=

 =
=
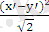
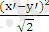 -
-
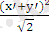
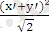 = - 2x'y'.
= - 2x'y'.
Бұдан x'y'= -


2. 3 Кеңістіктегі координаталар өстерін параллель көшіру
Кеңістікте декарттық тік бұрышты екі координаталар жүйесі Оху𝓏 және Ох ׳ у ׳ 𝓏 ׳ берілсін. Ох ׳ у ׳ 𝓏 ׳ координаталар жүйесі Оху𝓏 координаталар жүйесінен параллель көшіру нәтижесінде алынсын делік (43- сурет) . М нүктесі кеңістіктің кез келген нүктесі дейік және (x, y, 𝓏) пен (x', y', 𝓏') оның сәйкес Оху𝓏 және Ох ׳ у ׳ 𝓏 ׳ жүйелеріндегі координаталары болсын. О ׳ нүктесінің жүйесіндегі кооррдинаталарын (a, b, c) арқылы белгілейік.
Сонда векторларды қосудың үшбұрыш ережесі бойынша
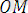
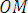 =
=
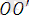
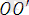 +
+
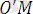
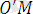 (1. 17)
(1. 17)
болады.
Бұл векторлар сәйкес нүктелердің радиус-векторлары болғандықтан, олардың координаталарын былай жазамыз:
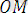
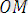 = (x, y, 𝓏) ,
= (x, y, 𝓏) ,
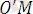
 = (x', y', 𝓏') ,
= (x', y', 𝓏') ,
 = (a, b, c) .
= (a, b, c) .
Енді бұл мәндерді (67) формулаға қойсақ, онда
x=x' + a, y = y' + b, 𝓏 =𝓏' + c . (1. 18)
Бұл формулалар бірінен - бірі параллель көшіру арқылы алынған координаталар жүйелеріндегі кез келген М нүктесінің сәйкес координаталары арасындағы байланысты көрсетеді.
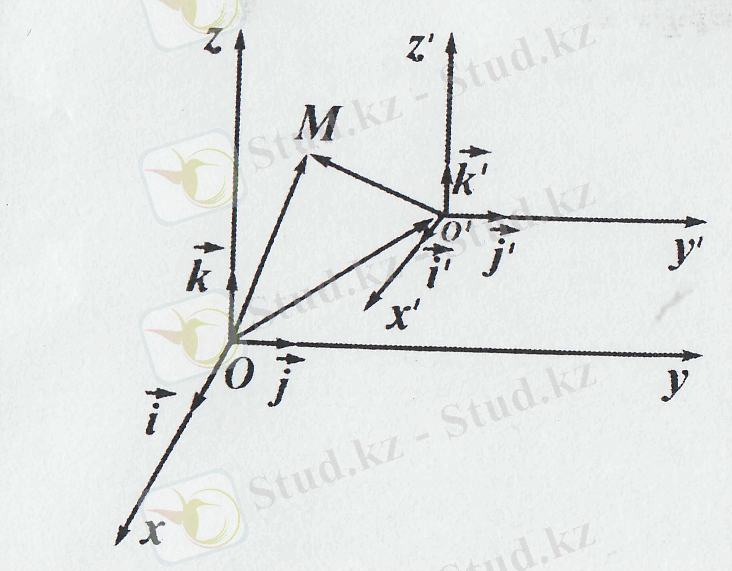
6 - сурет
2. 4 Кеңістіктегі координаталар өстерін бұру.
Бас нүктелері ортақ бір нүктеде жатқан Oxy𝓏 және Ox ׳ y ׳ 𝓏 ׳ декарттық тік бұрышты координаталар жүйелерін қарастырамыз.
Сонда
M(x, y, 𝓏) ⇔ =(x, y, 𝓏) ⇔ = x + y + 𝓏 ,
M(x ׳ y ׳ 𝓏 ׳ ) ⇔ =( x ׳ y ׳ 𝓏 ׳ ) ) ⇔ = x ׳ ׳ + y ׳ + 𝓏 ׳ ,
мұндағы ( , , ) және ( , , ) координаталар жүйелерінің сәйкес базистері.
Бұдан
x + y + 𝓏 x ׳ ׳ + y ׳ + 𝓏 ׳ ׳ (1. 19)
Егер бұл теңдіктің екі жағының да -ге скалярлық көбейтіндісін қарастырсақ, онда скалярлық көбейтудің үлестірілімдік заңы мен , , векторларының өзара пар-парлы (қос - қостан) ортонгональдығын ескеріп, мына теңдікті аламыз:
x=x ׳ ( ׳ ∙ ) + y ׳ ( ׳ ∙ ) + 𝓏 ׳ ( ׳ ∙ ) = x ׳ c os ( ׳ ) + y ׳ () +
Енді (1. 19) теңдіктің екі жағының да әуелі -ге, сосын - ға скалярлық көбейтінділерін қарастырсақ, oнда соңғы формулаға ұқсас формулалар аламыз. Демек,
x = α 11 x ׳ + y ׳ + 𝓏 ׳ ,
y = α 12 x ׳ + y ׳ + 𝓏 ׳ , (1. 20)
𝓏 = α 13 x ׳ + y ׳ + 𝓏 ׳ .
3. 1 Еселі интегралдар
Ω 1 , Ω 2 , . . . , Ω n - бөліктердің ең үлкен диаметрін нөлге ұмтылдыра отырып, V n = mΩ j қосындыдан алынған шекті айтуға болады.
mΩ j (1. 21)
Дене көлемін табу туралы есептен назарымызды аударып, (1. 21) өрнекке Ω жиынында анықталған f функциясына жүргізілетін амал деп қарaуға болады. Бұл амал f функциясыын Ω жиынында Риман бойынша екі еселі интегралдау амалы деп аталады, ал оның нәтижесін f функциясының Ω жиынында анықталған екі еселі (Риман) интегралы дейді де, V=
символдарының біреуімен белгілейді.
M= (1. 22)
Тағы да (1. 22) өрнекке Ω үш өлшемді жиынында берілген μ функциясына жасалған амал деп қарауға болады. Бұл амал (Риман бойынша) - үш еселі интегралдау амалы, ал оның нәтижесі анықталған үш еселі Риман интегралы деп аталады да,
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz