Математикадан оқу-әдістемелік топтама

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

МАТЕМАТИКАДАН ОҚУ-ӘДІСТЕМЕЛІК ТОПТАМА

« Жиын теориясы ұғымы: жиын ұғымы, жиын элементі, бос жиын, шекті және шексіз жиындар, тең жиындар, ішкі жиын, универсал жиын. Жиындардың берілу тәсілдері. Эйлер дөңгелектері» (1 сағат)

Жиын ұғымы анықтауға болмайтын алғашқы ұғымдардың бірі. Жиынды құрайтын объектілерді жиынның элементтері дейді. Жиындарды латынның бас әріптерімен, оның элементтерін кіші әріптерімен белгілейді.

Жиын мен оның элементтерінің арасындағы қатысты «тиісті», немесе «жатады» деген сөздермен беруге болады да, былай белгілейді ∈. Мысалы, «а объектісі А жиынына тиісті» деген сөйлемді былай жазып көрсетеді: а ∈ А. «b элементі А жиынына тиісті емес» деген сөйлемді былай жазып көрсетеді: b ∉ А, кейде b ∈ А.

Жиындар шекті, шексіз, бос жиын болуы да мүмкін. Бірде-бір элементі болмайтын жиынды бос жиын деп атайды да, оны былай белгілейді: ∅.

Жиындардың берілу тәсілдері

1. Жиынды оның элементтерін атап шығу арқылы беруге болады.

2. Жиынды оның элементтерінің бәріне бірдей ортақ сипаттамалық қасиетін көрсету арқылы беруге болады.

Мысалы жиын 1, 2, 3, 4, 5 сандарынан тұрса, ол жиынды былайша жазып көрсетеді А={1, 2, 3, 4, 5}.

Осы жиынды басқаша, екінші тәсілмен де беруге болады. А={x x ∈ Ν, x < 6}. Бұл жиын екінші тәсілмен беріліп тұр, атап айтқанда жиынның элементтері натурал сандар және 6-дан кіші болу қасиеттері көрсетілген.

Егер В жиынының кез келген элементі А жиынының да элементі болса, онда В жиыны А жиынының ішкі жиыны деп аталады, В ⊂ А символымен жазылады. Бос жиын кез келген жиынның ішкі жиыны болады. Сол сияқты жиынның өзі де өзіне ішкі жиын болады, яғни ∅ ⊂ А; А⊂А.

А-ның өзі және ∅ жиын меншіксіз ішкі жиындар деп аталады. Ал, А жиынының басқа ішкі жиындары, егер олар бар болса, меншікті ішкі жиындар деп аталады.

Мысалы А={a, b, c} жиынының алты меншікті ішкі жиындары {a}, {b}, {c}, {a, b}, {a, c}, {b, c} және екі меншіксіз ішкі жиындары ∅, {a, b, c} бар.

Егер А мен В біріне-бірі ішкі жиын болса, онда олар өзара тең жиындар деп аталады, яғни А ⊂ В және В ⊂ А болса, онда А=В.

Кейде бір I жиынының ішкі жиындарын қарастыруға тура келеді. Мұндай I эиынын универсал жиын деп атайды.

Әдебиеттер 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 16, 17

Жиындардың арасындағы қатынастарды Эйлер-Венн диаграммасы (дөңгелегі) арқылы кескіндеп көрсетуге болады (Эйлер /1707-1783/ - швейцар математигі, Петербург Академиясының мүшесі, Джон Венн /1843-1923/ - ағылшын математигі) .

а элементі А жиынына жатады, ал b элементі жатпайды.

• а • b

А мен В жиындарының бірдей, ортақ элементтері жоқ.

А В

А мен В жиындары тең.

А=В

В жиыны А-ның ішкі жиыны болады. .

Универсал I жиыны және оның ішкі жиындары.

А В D I

Әдебиеттер 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 16, 17

« Жиындарға амалдар қолдану: жиындардың қиылысуы және бірігуі, жиындардың айырмасы, толықтауышы. Қиылысу және бірігу амалдарының коммутативтік және ассоциативтік заңдары, қиылысу және бірігу амалдарын байланыстыратын дистрибутивтік заңы. Жиынды бір-бірімен қиылыспайтын ішкі жиындарға бөлу» (1 сағат)

Жиындардың қиылысуы

А мен В жиындарының қиылысуы деп А жиынында да, В жиынында да жататын элементтерден және тек солардан ғана тұратын жиынды айтады. А мен В жиындарының қиылысуы А ∩ В өрнегімен белгіленеді, ∩ таңбасы жиындардың қиылысу белгісі. Анықтаманы былай жазып көрсетуге болады:

А ∩ В = {х х ∈ А және х ∈ В}.

А мен В жиындарының қиылысуын Эйлер дөңгелектері арқылы көрсетейік.

А В

А ∩ В А ∩ В = ∅

Қиылысу амалының қасиеттері

Егер В ⊂ А, онда А ∩ В = В

А

В

А ∩ А = А
А ∩ ∅ = ∅
А ∩ I = A
А1∩ А2∩ А3∩…∩ Аn= {x x∈A1, x∈A2, x∈A3, …, x∈An}.

Жиындардың бірігуі

А мен В жиындарының бірігуі деп кемінде біреуінде жататын элементтерден және тек солардан ғана тұратын жиынды айтады. Жиындардың бірігуі А ∪ В өрнегімен белгіленеді. Анықтаманы былай жазып көрсетуге болады: А ∪ В = {х х ∈ А немесе х ∈ В}.

Екі жиынның бірігуін Эйлер дөңгелектері арқылы көрсетейік:

а) егер А мен В жиындары қиылысатын болса, онда олардың бірігуі

А В

б) егер А мен В жиындары қиылыспайтын болса, онда олардың бірігуі

А В

Бірігу амалының қасиеттері

Егер В ⊂ А, онда А ∪ В = А

А ∪ А = А
А ∪ ∅ = А
А ∪ I = I
А1∪ А2∪ А3∪ … ∪ An= {x x ∈ A1немесе x ∈ A2немесе x ∈ A3немесе … немесе x ∈ An}

Әдебиеттер 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 16, 17

Жиындардың айырмасы

А жиыны мен В жиынының айырмасы деп А жиынының В жиынында жатпайтын элементтерінен тұратын жиынды айтады. Айырманың анықтамасын былай жазып көрсетуге болады:

А\В = {х х ∈ А және х ∉ В}.

А мен В жиындарының айырмасын Эйлер дөңгелектері арқылы кескіндейік:

а) егер А мен В жиындары қиылысатын болса, онда А мен В жиындарының айырмасы штрихталған аудан

А В

б) А мен В жиындары қиылыспайды, онда

А В

В жиыны А жиынының ішкі жиыны болсын, яғни В ⊂ А.

В жиынындажатпайтын А жиынының барлық элементтерінің жиынын В-нің толықтауыш жиыны деп атайды. В жиынына толықтауыш жиынды В' _А таңбасымен белгілейді.

В' _А = {х х ∈ А және х ∉ В}

Енді Эйлер дөңгелегі арқылы кескіндейік

В В' _А

Екі жиынның айырмасының қасиеттері

А\А = ∅
А\∅ = А

Әдебиеттер 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 16, 17

Жиындарға қолданылатын амалдардың заңдары

Жиындардың қиылысуы және бірігуі коммутативті болады

А ∩ В = В ∩ А

А ∪ В = В ∪ А

Жиындардың қиылысуы және бірігуі ассоциативті болады

(А ∩ В) ∩ С = А ∩ (В ∩ С)

(А ∪ В) ∪ С = А ∪ (В ∪ С)

Жиындардың қиылысу және бірігу амалдарын байланыстыратын дистрибутивтік заңы орынды болады

А ∩ (В ∪ С) = (А ∩ В) ∪ (А ∩ С)

А∪ (В ∩ С) = (А ∪ В) ∩ (А ∪ С)

Мына теңдіктер орынды болады

А \ (В ∩ С) = (А \ В) ∪ (А \ С)

А \ (В ∪ С) = (А \ В) ∩ (А \ С) = (А \ В) \ С

(А ∩ В) ' = А' ∪ В'

(А ∪ В) ' = А' ∩ В'

Әдебиеттер 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 16, 17

« Жиындардың декарттық көбейтіндісі. Кортеж» (1 сағат)

(х; у) - реттелген пар, мұндағы х және у бұл пардың компоненттері. (х ₁ ; у ₁ ) = (х ₂ ; у ₂ ), егер х ₁ =х ₂ , ал у ₁ =у ₂ .

А мен В жиындарының декарттық көбейтіндісі деп, бірінші компоненті А-ға, екінші компоненті В-ға жататын элементтерден тұратын барлық парлар жиынын айтады.

Екі жиынның декарттық көбейтіндісін А×В өрнегімен белгілейді.

А×В = {(х; у) х ∈ А, у ∈ В}

Мысалы. А = {a, b, c}, B = {2, 3, 4}

А×В = {(a; 2), (a; 3), (a; 4), (b; 2), (b; 3), (b; 4), (c; 2), (c; 3), (c; 4) }

Декарттық көбейтіндінің қасиеттері

А × В ≠ В × А
(А × В) × С ≠ А × (В × С)

Әдебиеттер 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 16, 17

7. Лекция тақырыбы «Жиындардың декарттық көбейтіндісі. Кортеж» (1 сағат, жалғасы)

Егер х = {1, 2, 3, 4, 5} жиыны берілсе, онда осы жиынның элементтерін әртүрлі тәсілдермен реттеуге болады. Атап айтқанда, әртүрлі бір таңбалы, екі таңбалы, үш таңбалы, төрт таңбалы, бес таңбалы т. с. с. сандарды алуға болады. Басқаша айтқанда реттелген осындай жиын элементтерінің әртүрлі жиынтығын кортеж деп атайды, ал кортежді құрап тұрған элементтерді оның компоненттері дейді. Кортеждің компоненттерінің санын оның ұзындығы дейді. Кортежді былай белгілейді: (х ₁ ; х ₂ ; …; х _n ), n - кортеждің ұзындығы.

А ₁ , А ₂ , … А _n жиындарының декарттық көбейтіндісі деп бірінші компоненті А ₁ жиынына, екінші компоненті А ₂ жиынына, …, n-ші компоненті А _n жиынына жататын элементтерден тұратын, ұзындығы n-ге тең болатын барлық кортеждердің жиынтығын айтады.

Мысалы. А = {1, 2, 3}, B = {4, 5}, C = {6, 7}

A × B × C = { (1; 4; 6), (1; 4; 7), (1; 5; 6), (1; 5; 7), (2; 4; 6), (2; 4; 7), (2; 5; 6), (2; 5; 7), (3; 4; 6), (3; 4; 7), (3; 5; 6), (3; 5; 7) }

Әдебиеттер 1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 16, 17

« Комбинаторлық есептер: қосынды және көбейтінді ережелері» (1 сағат)

Саны шектеулі элементтерден әртүрлі комбинациялар құрастыруға және белгілі бір ереже бойынша құрастырылған барлық мүмкін комбинациялар санын есептеуге тура келетін жағдайлар жиі кездесіп отырады. Мұндай есептер комбинаторлық есептер, ал оларды шешумен шұғылданатын математика бөлімі комбинаторика деп аталады.

Көптеген комбинаторлық есептерді шешу үшін қосынды және көбейтінді ережелерін қолданады. Қосынды ережесі жиындардың бірігуіндегі элементтердің санын анықтауға мүмкіндік береді. Егер А мен В жиындары қиылыспаса, онда n(A∪B) = n (A) + n (B) . Егер А мен В жиындары қиылысатын болса, онда n(A∪B) = n (A) + n (B) - n (A∩B) .

А мен В жиындарының декарттық көбейтіндісіндегі элементтердің санын мына формула бойынша анықтайды: n(A×B) = n(A) ∗ n(B) .

Әдебиеттер 1, 2, 3, 5, 6, 7, 8, 9, 10, 15, 16, 17, 18

« Комбинаторика элементтері: орналастырулар, алмастырулар, терулер, олардың саны » (1 сағат)

Ұзындығы m болатын, n элементті Х жиынының элементтерінен құрылған осындай кортеждерді n элементтен m-нен жасалған қайталанатын орналастырулар деп атайды.

Олардың саны 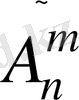символымен белгіленеді.

Сонымен, 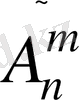= n ^m .

Ұзындығы m болатын, n элементті Х жиынының қайталанбайтын элементтерінен құрылған кортеждер жиынын n элементтен m-нен жасалған қайталанбайтын орналастырулар деп атайды.

Олардың санын 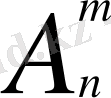Equation. 3 символымен белгілейді.

Сонымен, 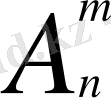Equation. 3 = n(n-1) …(n-m+1) .

n элементтен n-нен жасалған қайталанбайтын орналастыруларды n элементтен жасалған алмастырулар деп те айтады. Олардың санын P _n символымен белгілеп, мына формула бойынша табады P _n = n! = n(n-1) …3 · 2 ·1 .

Алғашқы n натурал сандардың көбейтіндісін «n- факториал» дейді, оны n! символымен белгілейді.

Бос жиынды бір ғана тәсілмен реттеуге болады, яғни P ₀ = 0!=1.

Әдебиеттер 1, 2, 3, 5, 6, 7, 8, 9, 10, 15, 16, 17

« Комбинаторика элементтері: орналастырулар, алмастырулар, терулер, олардың саны » (1 сағат, жалғасы)

Егер n элементті А жиынының m элементтен тұратын ішкі жиындарын құрастырсақ, сондай ішкі жиындарды n элементтен m-нен жасалған терулер дейді.

Терулер санын символымен белгілейді, оны мына формуламен табады = 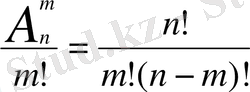Equation. 3