Екінші ретті дербес туындылы дифференциалдық теңдеулердің классификациясы мен канондық түрлендірулері
Екінші ретті дербес туындылы дифференциалдық теңдеулер классификациясы
Екі айнымалыдан тәуелді дифференциалдық теңдеулер.
Көп айнымалылы екінші ретті дифференциалдық теңеулер
. 3. Тұрақты коэффицентті тeңдeулердің жәй түрлері.
Белгісіз
\[u(x,y)\]
функциясы мен оның екінші реттіге дейінгі дербес туындыларын байланыстыратын
\[F{\bigl(}x,y,u,u_{x},u_{y},u_{x x},u_{x y},u_{y y}{\bigr)}=0\]
теңдеуін,
екінші ретті дербес туындылы дифференциалдық теңдеу
деп аталады. Тәуелсіз айнымалылары көп болғанда да теңдеу осы түрде жазылады.
\[a_{11}u_{x x}+2a_{12}u_{x y}+a_{22}u_{y y}+F\bigl(x,y,u,u_{x},u_{y}\bigr)=0\]
(1)
Жоғарғы ретті туындылары бойынша сызықтық делінеді, мұндағы
\[a_{i j}\left(x,y\right)\]
.
Егер
\[{\cal Q}_{i j}\left(\chi_{,}\,y_{,}\,M_{,}\,M_{x},M_{y}\,\right)\]
болса, онда теңдеу
квазисызықтық
деп аталады.
Теңдеу жоғарғы ретті туындылары
\[\bar{\cal M}_{\scriptscriptstyle X X}^{\phantom{A}}\,j d_{\scriptscriptstyle X y}\,j^{\scriptscriptstyle\prime}\]
, бойынша да, сондай-ақ функция U және бірінші ретті туындылары
\[\bar{\mathcal{M}}_{\scriptscriptstyle\chi,\mathsf{Z}}\bar{\mathcal{M}}_{\scriptscriptstyle\mathcal{N},\mathsf{Z}}\]
бойынша да, яғни
\[a_{11}u_{x x}+2a_{12}u_{x y}+a_{22}u_{y y}+b_{1}u_{x}+b_{2}u_{y}+c u+f=0\]
(2)
турінде болса,
сызықтық
деп аталады, мұнда
\[Q_{i j}\,\left(\chi_{},\,y\right)\]
,
\[b_{i}\left(x,y\right)c\left(x,y\right)f\left(x,y\right)\]
.
Егер коэффиценттері
\[a_{i j},b_{i},c\]
тұрақты болса, теңдеу
тұрақты коэффициентті
деп аталады. Кері түрлендірулері мүмкін болатын
\[x=\phi\]
\[\left(x,y\right)\]
),
\[\scriptstyle h\,=\,v\]
\[\left(x,y\right)\]
турлендірулерін таңдау жолымен, теңдеуге эквивалентті, жазылу турі жеңіл теңдеуге келеміз.
\[\begin{array}{l l}{{u_{x}=u_{x}x_{x}+u_{h}h_{x},}}\\ {{u_{y}=u_{x}x_{y}+u_{h}h_{y},}}\\ {{u_{x x}=u_{x x}x_{x}^{2}+2u_{x h}x_{x}\partial_{x}+u_{x h}\bar{a}_{x}\partial_{x}+u_{x}x_{x y}+u_{x}x_{x y}+u_{h}\eta_{y y},}}\\ {{u_{x y}=u_{x x}x_{x}^{2}+2u_{x h}x_{y}+u_{x t}x_{y y}+u_{x}x_{y y}+u_{x}x_{y y}+u_{x}\eta_{y y},}}\end{array}\]
(3)
Түрлендірулерді (3) теңдеуге (1) қойып, келесі теңдеуді аламыз.
\[\overline{{{Q}}}_{1}1M_{x x}\:+\overline{{{Z}}}Q_{12}M_{x h}\:+\overline{{{Q}}}_{22}M_{\eta\eta}\:+\overline{{{F}}}^{\prime}\longrightarrow\nonumber\]
(4)
\[\overline{{{a}}}_{11}=a_{11}{x_{x}^{2}}+2a_{12}{x_{x}x_{y}}+a_{22}\xi_{y}^{2},\]
\[\begin{array}{l}{{\overline{{{a}}}_{12}=a_{11}x_{x}h_{x}+a_{12}\bigl(x_{\mu}{}_{y}+h_{x}x_{y}\bigr)+a_{22}x_{y}h_{y},}}\\ {{\overline{{{a}}}_{22}=a_{1}h_{x}^{2}+2a_{1}h_{x}h_{y}+a_{22}\eta_{y}^{2}}}\end{array}\]
Мұнда
\[F{\bigl(}x,y,u,u_{x},u_{y}{\bigr)}=b_{1}u_{x}+b_{2}u_{y}+c u+f\]
болса, онда
\[\overline{{{F}}}=\left(\chi,h\,,u,u_{x}\,,u_{h}\,\right)\!\!=\!b_{1}u_{x}\,+\partial_{\,2}u_{\eta}\,+g u+\partial\]
, яғни бастапқы теңдеу сызықты болса, түрлендіруде сол күйі сақталады.
Коэффицент
\[{\overline{{a}}}_{11}=0\]
болуы үшін
\[a_{11}z_{x}^{2}+2a_{12}z_{x}z_{y}+a_{22}z_{y}^{2}=0.\]
(5)
теңдеуі қарастырылады.
Лемма
1.
Егер
\[z=\phi\left(x,\,y\right)\]
теңдеудің (5) шешімі болса, онда
\[\phi(x,y)=c\]
келесі теңдеудің
\[a_{11}d y^{2}-2a_{12}d x d y+a_{22}d x^{2}=0\]
(6)
теңдеуінің жалпы шешімі;
Лемма
2.
Егер
\[\phi(x,y)=c\]
теңдеудің (6) жалпы шешімі болса, онда функция
\[z=\phi\left(x,y\right)\]
(5) теңдеуді қанағаттандырады.
Теңдеу (6) бастапқы теңдеудің (1) сипаттаушысы (характеристикалығы) теңдеудің интегралдары оның сипаттаушысы (
характеристикалары)
деп аталады.
\[x=\phi\!\left(x,y\right)\]
десек
\[u_{{\xi_{t}},\nonumber}\]
-дің коэффиценті нөлге айналады,
\[\psi\,=(x,y)=c o n s t\]
теңдеудің (6) жалпы интегралы болса, онда
\[h=\phi(x,y)\]
десек
\[M_{\eta\bar{\eta}}\]
-ның коэффициенті нөлге айналады.
Теңдеу (6) келесі теңдеулерге жіктеледі:
\[\frac{d y}{d x}=\frac{a_{12}+\sqrt{a_{12}^{2}-a_{11}a_{22}}}{a_{11}},\]
(7)
\[\frac{d y}{d x}=\frac{a_{12}-\sqrt{a_{12}^{2}-a_{11}a_{22}}}{a_{11}}.\]
(8)
Түбір астындағы өрнектің таңбасы теңдеудің
\[a_{11}u_{x x}+2a_{12}u_{x y}+a_{22}u_{y y}\]
\[{}+F\]
\[\mathbf{\partial}=0\]
түрін анықтайды.
\[\mathrm{D}(M\,)=a_{12}^{2}(M\,)-a_{11}(M\,)a_{22}(M\,)\]
\[M(x,y)\]
десек, М нүктесінде теңдеу
1. гиперболалық тектес деп аталады, егер
\[\Delta(M)\]
>0 болса,
2. параболық тектес деп аталады, егер
\[\mathrm{D}(M)=0\]
болса,
3. эллиптикалық тектес деп аталады, егер
\[\operatorname{D}(M)<0,\]
болса
1.
\[\operatorname{D}(M)\gg0\]
болса,
\[x\,=\phi(x,\ y),\]
\[h=\psi\left(x,y\right)\]
десек, теңдеу
\[u_{x h}\,=\Phi\!\left(x,\eta\,,u,u_{x}\,,u_{\eta}\,\right)\]
,
\[\mathbf{F}=-{\frac{\overline{{F}}}{2a}},\]
гипербола тектес канондық ( жәй ) түріне келеді.
Практикада келесі түрдегі канондық теңдеулер де қолданылады. Алмастырулар жасаймыз.
\[x=a+\beta\,,\]
\[h=a-{\boldsymbol{\beta}}\]
, немесе
\[a\,={\frac{x+\eta}{2}}\,,\]
\[b={\frac{x-\eta}{2}}\]
десек теңдеу мына канондық түріне келтіріледі.
\[u_{a a}\ -\ W_{\beta\beta}\ =\Phi_{1}\]
2.
\[\wedge_{\mathfrak{L}}\]
(M) =0 болса,
\[\phi\!\left(x,y\right)=c o n s t\]
үшін
\[\forall\eta\left(x,y\right)\]
функциясын,
\[{\phi}\left(x,y\right)\]
Функциясынан тәуелсіз таңдаған, алмастырулар нәтижесінде парабала тектес теңдеудің канондық түрін аламыз
\[u_{h h}\,=\Phi\!\left(x\,,\eta\,,u,u_{x}\,,u_{\eta}\,\right)\]
,
\[\begin{array}{l l}{{\dot{\Omega}}}&{{\overline{{F}}}}\\ {{\overline{{\mathrm{C}}}}}&{{-\,-\,\frac{R}{Q_{22}}\,\dot{\phi}.}}\end{array}\]
3.
\[\Delta(M)\]
<0, болса,
\[\phi(x,y)=c\]
, (7) теңдеудің комплекс интегралы десек,
\[\phi*(x,y)=c\]
оған түйіндес (8) теңдеу шешімі
\[x=\phi(x,y)\]
,
\[h=\phi^{**}(x,y)\]
алмастыруларымен
\[a={\frac{j\,+\,\phi^{\mathrm{st}}}{2}},\]
\[b={\frac{j-\phi^{*}}{2i}}\]
,
онда
\[x=a+i\beta\,,\]
\[h=a-i\beta\]
дей отырып, эллиптикалық тектес теңдеудің канондық
түрін аламыз.
\[\frac{\vec{\alpha}}{\hat{\mathrm{e}}}\hat{O}=-\ \frac{F}{a_{22}}\,\hat{\mathrm{e}}\]
Сонымен
\[\Delta(M)\]
<0, (гиперб. тектес)
\[u_{x x}-\,u_{y y}=\mathbf{F}\,,u_{x y}=\Phi\]
\[\operatorname{D}(M)<0,\]
(эллиптик. тектес)
\[u_{x x}+u_{y y}=\Phi\]
\[\operatorname{D}(M)=0,\]
(парабола тектес)
\[u_{x}=\Phi\]
2. Нақты коэффиценттерімен сызықтық дифференциалдық теңдеуді
Келесі түрлендірулермен
\[{\cal x}_{\,_{k}}=\xi_{_{k}}\bigl(x_{_{1\dots}}x_{_{n}}\bigr)\bigl(k=\overline{{{1,n}}}_{y}\]
,
\[u_{x_{i}}=\mathop{{\Delta}^{\circ}}_{k=1}^{a}u_{x_{k}}a_{_{i k}},u_{x_{i}x_{j}}=\underbrace{{\frac{a}{\Delta}}^{\circ}{\stackrel{\circ}{\Delta}}^{\circ}}_{l=1}^{a}u_{x_{k}x_{l}}a_{_{i k}}a_{_{j l}}+\sum_{k=1}^{n}u_{_{\xi_{k}}}(\xi_{k})x_{_{i}},\]
\[a_{_{i k}}=\frac{\mathbb{R}_{k}}{\partial x_{i}}\]
канондық түрге, екі айнымалыдағы әрекеттермен келтіруге болады. Бастапқы теңдеу мына түрге келтіріледі.
\[\sum_{k=1}^{n}\frac{s}{\lambda_{\ k l}}u_{x_{i}x_{l}}+\frac{s}{\lambda}^{n}\,\overline{{{b}}}_{k}u_{\xi_{i}}\,+c u+f=0\]
\[\overline{{{a_{k l}}}}=\underline{{{a}}}^{a}\stackrel{\stackrel{\leftarrow}{\Delta}}{\Delta}_{j=1}^{a}a_{i j}a_{\ i k}a_{\ j l},\stackrel{\longrightarrow}{\bar{b}}_{k}=\underline{{{a}}}^{a}~b_{i}a_{\ i k}+\sum_{i=1}^{n}\stackrel{\stackrel{\leftarrow}{\partial}}{\Delta}a_{i j}(\xi_{k})_{x_{i}x_{j}}\]
Квадраттық түрлер
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар


 Егер коэффиценттері
Егер коэффиценттері
 (6)
(6)
 ,
,

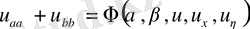
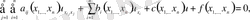 (9)
(9)