Пуанкаре - Ляпунов әдісімен жазықтық дифференциалдық жүйелерінің тұрақтылығы мен шекті циклдерін анықтау

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Диференциал теңдеулердің тұрақтылық белгілерін анықтаудың Пуянкаре-Ляпунов Әдісі

Болжап жатамыз, мысалы не облыста G туралы екі тұйық сызық түрінде салған 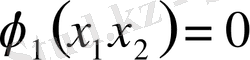және 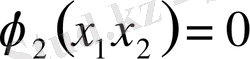, екі айналма облыс және бар болушылар еместер өзі кесіп өтеді.

Мүмкін жазықтық векторлары 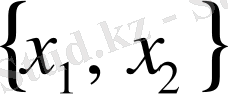поляр сызықтарда 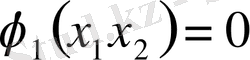және 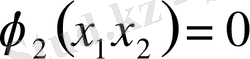бағытталған немесе тек қана ішіне немесе тек қана сыртқы сахина бөліміне . Егер мына шарт жанында, жоқ болып сахина ішінде жүйе тыныштығы нүктелердің аралығы (1), ал интеграл қисықтар жеткілікті дұрыс орналасқан, онда дәлелдеу мүмкін болған сахина ішінде бар болып жатыр бірақ бір шектің жүйе циклі (1) .

Үлгіде жалпы мынаны түсіндіріп жатырмыз .

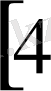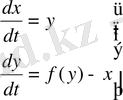(2)

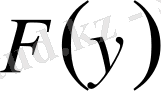толысыз айқын болып жатыр. 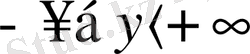және сонымен қатар 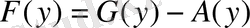, қайда тұрақты сан мен функция 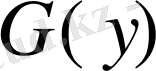туралы кейінгі жағдай. Келесі шарттар қанағаттандырып жатыр.

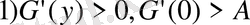
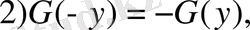т. б. Туралы 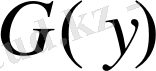жұпсыз функция у;

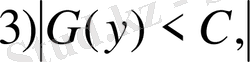т. б. туралы 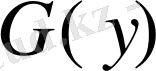дәлелдеп жатыр не жүйе аралығы (2) жоқ бірақ, бір шекті цикл, егер тек қана 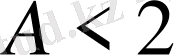екі қисық контактісіз үшін мынаны салып жатырмыз, (0, 0) тыныштық нүкте қоршаған және бір сыпыра айналма шек облыс қойылған. Алдымен жоғарғы жазықтықта қарап шығып жатырмыз. (См. Сурет. 2) қайда .

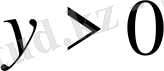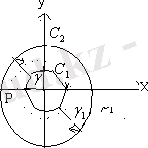сурет-2

Қосалқы теңдеуді содан кейін қарап шығып жатырмыз.

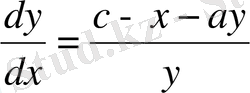
Егер - интеграл қисық мына теңдеудің, жоғарғы жарты жазықтықта жатқан теңсіздік байланысты (*) жүйе жазықтық векторы (2) мына сызықтар тыймайды. Демек, бар сызық контактісіз.

Сондай сызықтардың теңдеуін жеңіл алу дәл осындай қарапайым сияқты теңдеу жеңіл интегралданады. Нақты жүйені тиісті қарастырып жатырмыз.

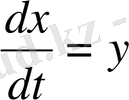
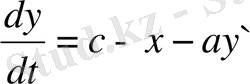
Болжап жатырмыз, не 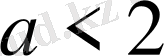сол уақытта жеңіл табамыз немесе

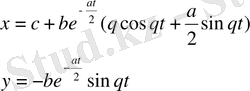
Мұнда 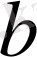тұрақты, қанағаттандырып жатыр.

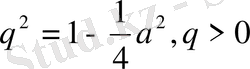. Шарт орындалды. .

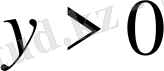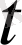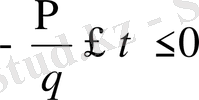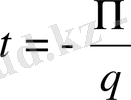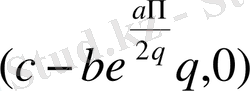Сол уақытта өзгерту үшін шектерді есептейміз, , өзгеріп жатыр. Өзгергіш және нүкте сәйкестігі , және жауап беріп жатыр, және нүкте сәйкестігі және 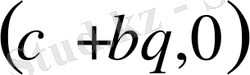қисық . Бұларды нүктелерде мен қисық кесіп өтіп жатыр ОХ .

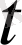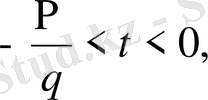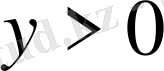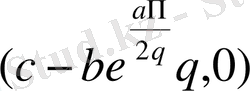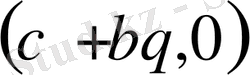Егер интервалы арқылы ауыстырылса, тұрақты , және мына аралықтан мағыналарына арналған сондықтан қисық кесіп өтпейді ОХ жоғарғы жарты жазықтықта жатыр. Талап етіп жатырмыз, нүкте үшін және нүкте салыстырмалы (0, 0) .

Төменгі жарты жазықтықтар доғаны қазір симметриялық елестету жолымен координаталардың басы салыстырмалы көрсетілгенінен доға жоғарырақ . Доғалардың екеуінің бірігуінен координаталарды бірсыпыра тұйық қисық, бас қоршалған болып шығып жатыр. Оны С арқылы белгілеп жатырмыз. Егер осьпен оны кесіп оту нүктелері шығару ОХ, жүйеге арналған (2) контактісіз келіп жатыр. Арғы бөлімге арналған қисықта, теорияны орнында жоғарғы жарты жазықтықта болып жатыр. Оған қоса жүйе жоқ болуы жазықтық вектор арасы (2) мынаның қисық теңсіздіктерге еріп жатыр. (*) оны қарап шығуды талап етеді. Ол үшін көріп жатырмыз егер нүктеде (х, у) жазықтық векторына байланысты емес 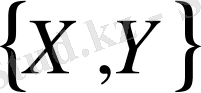, жұптылығының 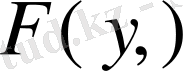нүктеде 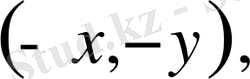симметриясының 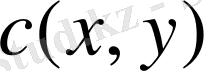нүкте салыстырмалы (0, 0) , жазықтық векторы бар.

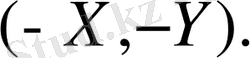
Төменгі жарты жазқтықта сондықтан доға координаталардың басы салыстырмалы жоғарғы жарты жазықтықтар доға мен оның симметриялы белгінің жоғарырақ векторлық құрылымының не доға контактісіз жоғарғы жарты жазықтықта доға бар, векторларды жүйе жазықтықтары (2) доғаларды төменгі (жарты жазықтықта) тоқталымайды.

Жиында, тұйық сызық С (егер оның нүктелерді шақыру кесіп етудің ОХ осьпен) контаксіз қисық бар.

Ось нүктелерінде ОХ қисық С толысыз айқын жазықтық векторын сонымен қатар бағытталып жатыр. Бірақ, шектер т. б. бұларды нүктелерде жазықтық С векторларына тиіп жатыр. Қалған нүктелерде С векторы, қандай жеңіл тексеру С тура ішке бағытталған .

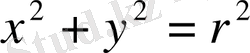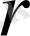Тұйық қисық біреуін тағы контаксіз біреуді салып жатырмыз (0, 0) . Екеуіне де тиісті, ең алдымен ішінде жату жеткілікті т. б. тиісті болу. Мұнда дұрыс табылған. Азайтып жатырмыз, егер дұрыс 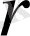барлығының 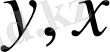қайсысының 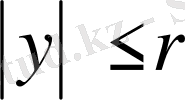, функция 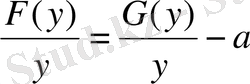дұрыс болды. Оны істеу шарт байланысы үшін бір функцияға арналған

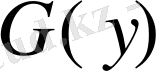
Шынында, 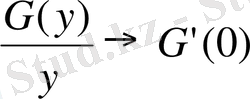туралы 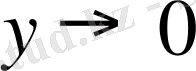және 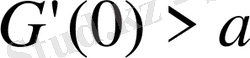демек, 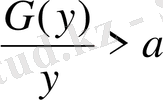туралы , т. б. егер 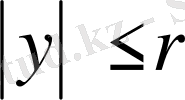, қайда 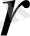жеткілікті .

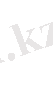
Мұнда көрсетілген саны бекітілген .

Дәлелдеу, не шеңбер 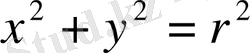жүйе үшін (2) контаксіз (егер осьпен оны кесіп өтуі нүктелері шығару ОХ) .

Жанама шеңберге бағыт болып жатыр 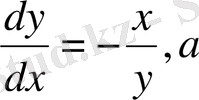жүйе векторлық жазықтық (2) шеңбер мына нүктеде бағытталып жатыр.

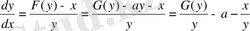Шеңбер поляры сондықтан барлық жерде 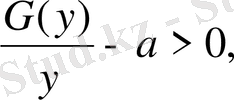еріп жатыр, немесе жазықтық вектор бағыты шеңберге жанама бағытын беріп жатыр (ось нүктелері басқа ОХ ) мынау және білдіріп жатыр ось нүктелері шығара ОХ 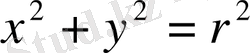жүйе үшін (2) келіп жатыр қисық контаксіз.

Сонда мына шеңбер бағыттарын деп белгілеп жатырмыз. нүктелерінде басқа оны кесіп өтуі екі нүктенің ОХ осьпен жүйе жазықтық векторын жиынында , сыртқы бөліміне тура бағытталған айналма облыс бейнеленген суреттерге екі және шек қойылған контаксіз қисықтар С және .

Шекарасында оның айналма облыстары т. б. қисықтарды С және векторларды жүйе жазықтықтары, жоғарырақ айтылған қандай мына облыстарды ішке бағытталған. Осы жоғарыда жеңіл дәлелдеуге болатын облыс үшін бар болып жатыр, бірақ бір жүйе айтарлықтай цикл (2) .

Жеңіл тексеру тек қана бір жүйе (2) болып жатыр. Тек бір нүктелердің (0, 0) , және сондықтан жоғарырақ көрсетілген айналма облыстарды нүктенің орны жоқ.

Қандай болсмасы Р нүктесін қарап жатырмыз 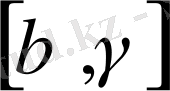(см сур. 2) және бақылап жатырмыз бұрыс үшін дұрыстың, мына нүктеге тиісті теңдеулерден (2) табамыз, не Р нүктесінде тура 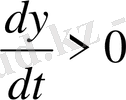т. б. жарты жазықтық, ал 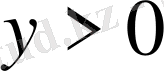, жоғарғыны жүріп жатыр, ол былай 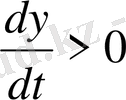, және жарты жазықтық дәл осылай жүріп жатыр, Х осьі осіп жатыр. Алдыңғының не жазықтық векторларын бағытталған сақина ішке еріп жатыр, не жарты жазықтық жоғарғы жартылай шектерінің артынан. Нәтижесінде мына жартылай жазықтықты 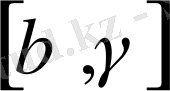кесінді кесіп өтіп жатыр.

Ұқсастығын дәлелдеп жатыр немесе ол төменгі жартылай сақина ішінде одан әрі барады және 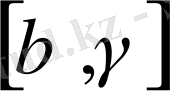кесінді тағы бір кесіп өтеді.

Функция 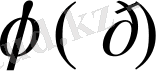толысыз 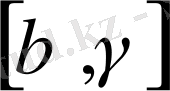толысыздық үшін жүйе шешімдері (2) бастапқы тап осыларға . Сонымен қатар, соңғы 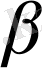нүктесіне 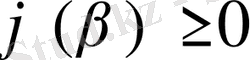, ал соңғы нүктеге 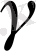қойып жатырмыз 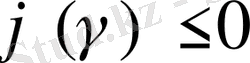, дәл осылай жарты жазықтықтармен дұрыстар сияқты мына нүктелерге жауап беріп жатырмыз сақина шектерінің артынан шығарылады.

Егер 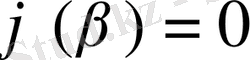немесе 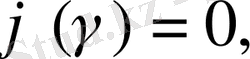онда шекті цикл бар болуы анықталған, дәл осылай лайықты қисық интеграл сияқты тұйық болады.

Мұнда 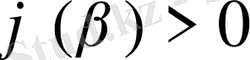және 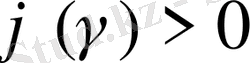. Сол уақытта функцияға қолдануды 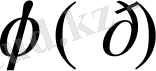түбір туралы теорема мына қағида бар 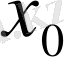нүктесі 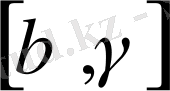қайсысының 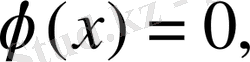туралы. Бұл белгілі, не қисық интеграл 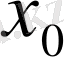нүктесі арқылы өтетін тұйықтық .

Сонымен жүйе (2) болып жатыр 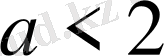ешбір цикл.

Ескертпе. Тура дәлелденген жүйе (2) болып жатыр, бірақ біреуі тұйық қисық интеграл. Бірақ анықтамамен, тұйық қисық интеграл айтарлықтай циклмен келіп жатыр. Егер үйлесімді тар сақинада толық емес қисық интеграл тұйық келіп жатыр. Өйткені тура дәлелдердің артынан сондықтан шекті цикл алдымен талап етіп жатыр не ешкімнің Р нүктесіне 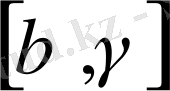тұйық қисық интеграл жауап беріп жатыр.

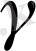нүктені тексеріп шығамыз. Жеңіл көрсету жарты жазықтыққа жағымсыз оған тиісті (0, 0) бір қалыпты нүктеге ұмтылып жатыр. Оны көріп шығуды талап етіп жатыр, не тексерілген жоғарырақ және барлық аз радиус шеңберлері және орталық қисық (0, 0) айтарлықтай контаксіз қисық және жағымсыз жарты жазықтық бағытпен сырттан ішке.

Осы арада келіп жатқан жарты жазықтық әрбір сондай қауырсында көрсетілген шеңбер жүйесінің сондықтан (0, 0) нүктеге . Осы арадан нүкте арқылы қисық интеграл өтетін мүмкін емес тұйықтық. Егер функцияға қайту 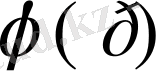, онда ол мынаны білдіріп жатыр, 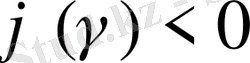. Демек, 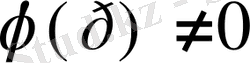тұрақты .

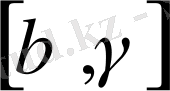Мына 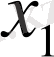нүктемен келіп жатыр. Осы уақытта оған жауап беріп жатқан қисық интегралды жүйе (2) , ал, 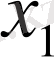қандайда 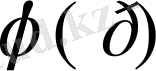функциямен үйлесімді тар сақинада, қисық интегралды қоршайды. Тұйық қисық интеграл 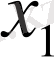нүктесі арқылы өтетін цикл бар екенін білдіріп жатыр.