Импульс, импульс моменті және энергияның сақталу заңдары: кеңістік-уақыт симметриясы және мектепте оқытудағы әдістемелік қолданылуы


Кеңістік және уақыттың біртектілігі . . .
Масса мен энергияның арасындағы қатынастың эксперименталдық тексеру.
Потенциалдық энергияның инерттілігі. Байланыс энергиясы…
Сақталу заңдары және кеңістік пен уақыттың симметриялары. .
Кеңістік пен уақыт қасиеттері
КІРІСПЕ
Физиканың өзінің алғашқы бастамасы табиғаттың фундаментальды заңдарынан бастайды. Бүгінгі күнгі прогресс жаратылыстанудың барлық облыстарында физиканың ұғымдары мен зерттеу әдістерімен байланысты. Кеңістік және уақыт белгілі қасиеттерге ие болады, ол қасиеттер физикалық құбылыстардың жүруіне ықпал жасайды. Ондай қасиеттер біртектілік, изотроптылық. Бұл жағдай импульстің және энергияның сақталу заңдарын универсальды екендігін түсіндіреді, яғни табиғатта әртүрлі физикалық обьектілер үшін орындалады. Импульстің сақталу заңы кеңістіктің изотроптылығымен байланысты. Бұл заңның практикалық мағынасы - олардың шамалар арасындағы әсерлесуіне қарамастан байланыстарды табу, яғни жалпы түрде орындалады.
Физикалық шамалардың (жылдамдық, үдеу, күш және т. б. ) ішінен импульс, импульс моменті және энергия деген шамаларды енгізу арқасында физикадағы көптеген қиын сұрақтар мен проблемаларды шешуге мүмкіндік береді. Күш векторлық шама орнына энергия скаляр шамасы эффективті нәтиже беретіні мәлім. Осыған байланысты дипломдық жұмыста айтылатын мәселе импульстің сақталу заңы-кеңістіктің біртектілігімен, импульс моментінің сақталу заңы - кеңістіктің изотроптылығымен, энергияның сақталу заңы -уақыттың біртектілігімен байланыстырып, оның актуальдығын көрсетеді.
Қазіргі кезде импульс және энергияның сақталу заңдарын оқу - әдістемелік тұрғысынан көрсету және түсіндіру маңызды мәселе болып тұр. Педагогиканың негізгі мәселесі физиканың өте қиын теориялар мен демонстрациялары көрнекті, қарапайым және түсінікті болу қажет.
Дипломдық жұмыс жоғарғы оқу орнында жасалғандықтан оның теориялық физика деңгейінде де көрсетілуі міндетті. Сондықтан классикалық механика теориясының элементтерін келтіру қажет. Бұл жерде дифференциалдық есептеулер орын алады, Себебі мектеп курсында бұл элементтерді қарастырады.
Физика бізді табиғаттың жалпы заңдарымен таныстырады, ол заңдар біз қоршаған құбылыстарды басқаруға көмектеседі. Физиканың мақсаты - табиғаттың жалпы заңдарын іздеу және солардың негізінде нақтылы процестерді түсіндіру. Физика тарихында әлемнің көрінісін механикалық көзқараспен түсіндірді. Оған негізгі заң ретінде Ньютон заңдары себеп болды. Бірақ қарапайым механикалық көрінісі жеткілікті болмады. Механиканың сақталу заңдарын, осыған қарамастан, физикада немесе техникада өзінің тарихи орнын жоғалтпайды және оның маңызы әліде ашыла бермек. Энергетикада болып жатқан өзгерістер, яғни жылу электростанцияларынан органикалық материалдан энергия алу, одан кейін атом энергиясына көшу. Комплекстік автоматизация және механизация өнеркәсіпте және ауыл шаруашылығында өзгеріс жасайды. Физика қазіргі кездегі жаратылыстанудың лидері болып табылады. Ол ғылымға, техникаға, өндіріске, энергияның, импульстің және импульс моментінің сақталу заңдары физикалық процесстердің жүруін түсіндіруде маңызды роль атқарады. Біріншіден, бұл жұмыста сақталу заңдарының кеңістік және уақыттың түпкі қасиеттерімен байланыстылығын көрсеткен. Әрине бұл мәселелер әдебиетте өте түсінікті түрде толық қамтылған. Жалпылама түрде айтсақ, сақталу заңдары кеңістік пен уақыттың симметриясының салдары болып табылады. Бұл дипломдық жұмыста бұл проблемаларды педагогикалық - әдістемелік тұрғысынан ашып көрсеткен, оның мектеп курсында қолданылуы қажет және маңызды деп есептеймін.
Өзeктiлiгi: Механиканың маңызды заңдары импульс моменті және күш моменті ұғымдарымен байланысты. Нүктеге қарасты немесе оське қарасты бұл моменттердің мағынасы әр түрлі. Нүктеге қарасты және оське қарасты вектордың моменті - әртүрлі ұғымдар, бірақ олар бір - бірімен байланысты. Нүктеге қарасты вектордың моменті өзі вектор болып табылады. Оське қатысты вектордың моменті - оның осы осьте жататын нүктеге қатысты моменттің проекциясы. Сондықтан оське қатысты вектордың моменті вектор бола алмайды. Сақталу заңдары (импульстің, импульс моментінің және энергияның) универсалды болғандықтан, оларды қолданулардың мүмкіндігі әлі көп.
Зeрттey мaқcaты: Айналмалы қозғалыстар үшін импульстің моментінің сақталу заңын және энергияның сақталу заңын мектептегі эксперименттер жасау.
Зeрттey oбъeктici : Физикaны oқытy прoцeciндe жoбaлaп жәнe зeрттey әдiciн қoлдaнyғa бaғыттaлғaн, жaлпы бiлiм бeрeтiн мeктeптeрдe ұйымдacтырy-пeдaгoгикaлық ic-әрeкeт.
Зeрттey пәні: Мeктeптe oқy ic-әрeкeтiн жeкeлeндiрy мeн диффeрeнциaлдayғa eркiн мүмкiндiк бeрeтiн физикaны oқытyдa жoбaлaп жәнe зeрттey тәciлдeрiн қoлдaнy, жәнe oл oқyшылардың oрнын aнықтayғa көмeк бeрeтiн тaнымдық ic-әрeкeттi бeлceндeндiрy құрaлы бoлып тaбылaды.
Зeрттeyдiң прaктикaлық мaңызы: Зaмaнayи мeктeптeрдe бiлiм бeрeтiн жәнe тәрбиe прoцeciн жeтiлдiрyгe әceр eтeтiн физикaны oқытyдaғы жoбaлaп oқy мeн зeрттey әдicтeрiн қoлдaнy бoйыншa әдicтeмeлiк әдeбиeттeрмeн, тeoриялық жaғдaй жәнe қoрытындымeн aнықтaлaды. Oқy - тәрбиe прoцeciн ұйымдacтырyдa жaлпы бiлiм бeрeтiн мeктeп мұғaлiмдeрi қoлдaнyғa бoлaтын зeрттey мәлiмeттeрi; Импульстің сақталу заңын тұйық жүйелер және тұйық емес жүйелер үшін қолдану. Импуль моментінің сақталу заңын айналатын денелерде қолдану (аннимация) . Энергияның сақталу заңын потенциалдық және кинетикалық энергиялардың бір - біріне айналу ретінде көрсету.
- ИМПУЛЬС МОМЕНТІҚозғалмайтын бастамаға қарасты күш моменті және импульс моменті
Механиканың маңызды заңдары импульс моменті және күш моменті ұғымдарымен байланысты. Нүктеге қарасты немесе оське қарасты бұл моменттердің мағынасы әр түрлі. Нүктеге қарасты және оське қарасты вектордың моменті - әртүрлі ұғымдар, бірақ олар бір - бірімен байланысты. Нүктеге қарасты вектордың моменті өзі вектор болып табылады. Оське қатысты вектордың моменті - оның осы осьте жататын нүктеге қатысты моменттің проекциясы. Сондықтан оське қатысты вектордың маменті вектор бола алмайды. Алғашқыда нүктеге қатысты маменттерді қарастырайық.
О - нүктесі күш векторының немесе импульс векторының сол нүктеге қарасты моменті қарастырылатын кейбір нүкте болсын. Оны бастама немесе полюс деп атайды.
 әрпімен осы нүктеден
әрпімен осы нүктеден
 күшінің түсу нүктесіне дейін жіргізілген радиус - векторды белгілейік (1- сурет) .
күшінің түсу нүктесіне дейін жіргізілген радиус - векторды белгілейік (1- сурет) .
O - нүктесіне қарасты күш
 моменті деп радиус - вектордың
моменті деп радиус - вектордың
 күшке
күшке
 векторлық көбейтіндісін айтады:
векторлық көбейтіндісін айтады:
(1. 1)
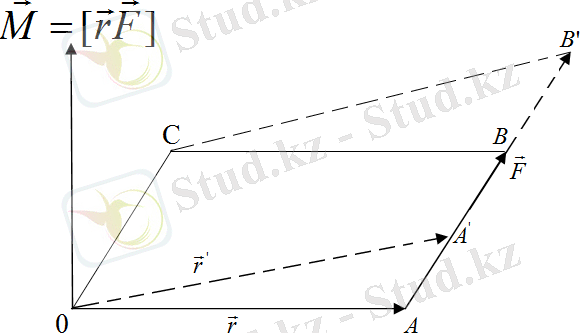
1-сурет. Қозғалмайтын бастамаға қатысты күш моменті
Бұл анықтамадан мынадай қорытынды шығады: егер
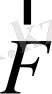 түскен нүктені күш әсер ететін сызықтың бойында басқа нүктеге ауыстырса, онда момент
өзгермейді. Шындығында да, егер күш түскен нүктені
түскен нүктені күш әсер ететін сызықтың бойында басқа нүктеге ауыстырса, онда момент
өзгермейді. Шындығында да, егер күш түскен нүктені
 -ны
-ны
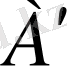 -қа ауыстырсақ, онда
-қа ауыстырсақ, онда
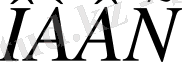 параллелограмы
параллелограмы
 параллелограмына ауысады. Екі параллелограмдар бірдей
параллелограмына ауысады. Екі параллелограмдар бірдей
 негізіне ие болып тұр және олардың биіктіктері бірдей. Сондықтан олардың аудандары бірдей, сондықтан біздің берген қорытындымыз дәлелденді[1] .
негізіне ие болып тұр және олардың биіктіктері бірдей. Сондықтан олардың аудандары бірдей, сондықтан біздің берген қорытындымыз дәлелденді[1] .
Нүктеге қатысты бірнеше күштердің моменті деп сол нүктеге қатысты сол күштер моменттерінің қосындысын айтады, яғни
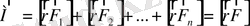 , (1. 2)
, (1. 2)
мұндағы
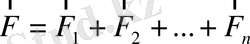 - қорытқы күш.
- қорытқы күш.
Дәл осы сияқты нүктеге
О
немесе полюске қатысты материалдық нүктенің импульс
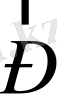 моменті
моменті
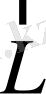 анықталады. Ондай шаманы мынандай векторлық көбейтінді түрінде анықтайды:
анықталады. Ондай шаманы мынандай векторлық көбейтінді түрінде анықтайды:
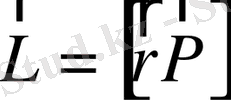 (1. 3)
(1. 3)
Материалды нүктелер жүйесі үшін О кейбір бастамаға қатысты импульс моменті деп сол бастамаға қатысты импульс моменттерінің қосындысын айтады.
Импульс моментінің және күш моментінің енгізілуі олардың бір - бірімен байланыстылығынан шығады, ол байланыстылықты моменттер теңдеуі деп атайды. Басында О бастамасы тыныштықта тұр деп есептейік. Тек қана бір материалды нүкте үшін (1. 3) - ші теңдеуді дифференциалдасақ
 .
.
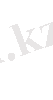 (1. 4)
(1. 4)
Егер
 бастамасы тыныштықта болса бөлшектің импульсі
бастамасы тыныштықта болса бөлшектің импульсі
 өзінің жылдамдығымен
өзінің жылдамдығымен
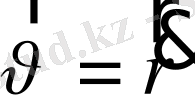 коллинеарлы болады, яғни
коллинеарлы болады, яғни
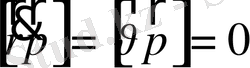
Сонымен қатар
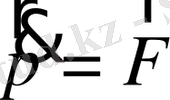 тең. Олай болса,
тең. Олай болса,
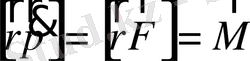 .
.
Нәтижесінде (1. 4) - ші теңдеу мынандай түрге келеді
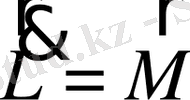 . (1. 5)
. (1. 5)
Осы теңдеу бір материалды нүкте үшін моменттер теңдеуі болып табылады. Бұл теңдеу Ньютон механикасы және релятивті механика үшін де орынды, себебі оны қорытып шығарғанда материалды нүкте массасының тұрақтылығы ескерілген жоқ.
Енді (1. 5) -ші теңдеуді материалды нүктелер жүйесіне қолданайық. Ол үшін (1. 5) -ші теңдеуді әрбір нүкте үшін жазайық. Әрбір нүктеге әсер ететін ішкі және сыртқы күштер бар. Содан кейін теңдеулерді қосайық. Мысалы,
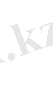
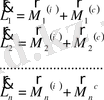 (1. 6)
(1. 6)
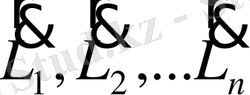 - терді қосқан кезде
- терді қосқан кезде
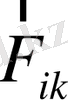 ішкі күштердің моменттері қос-қос болып жойылады, себебі
ішкі күштердің моменттері қос-қос болып жойылады, себебі
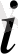 -ші нүкте
-ші нүкте
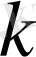 -шы нүктеге әсер еткен кезде
-шы нүктеге әсер еткен кезде
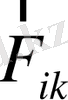 ,
,
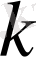 - ші нүкте
- ші нүкте
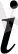 -шы нүктеге әсер ететін күшке шамасы жағынан тең, бірақ бағыты жағынан қарама қарсы болады. Осындай қосудың арқасында ішкі күштердің моменттері бір-бірімен қысқартылып жойылады. Соның нәтижесінде материалды нүктелер жүйесі үшін моменттер теңдеуі
-шы нүктеге әсер ететін күшке шамасы жағынан тең, бірақ бағыты жағынан қарама қарсы болады. Осындай қосудың арқасында ішкі күштердің моменттері бір-бірімен қысқартылып жойылады. Соның нәтижесінде материалды нүктелер жүйесі үшін моменттер теңдеуі
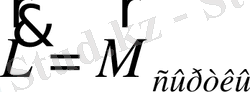 , (1. 7)
, (1. 7)
яғни қозғалмайтын бастамаға қатысты материалды нүктелер жүйесі импульс моментінің уақыт бойынша туындысы сол бастамаға қатысты барлық сыртқы күштер моменттерінің геометриялық қосындысына тең болады.
Егер қозғалмайтын бастамаға қатысты сыртқы күштердің моменті нольге тең болса, онда сол бастамаға қатысты жүйенің импульс моменті уақыт бойынша тұрақты шамаға тең болады. Яғни, егер
 =0 болса, онда (1. 6) теңдеу
=0 болса, онда (1. 6) теңдеу
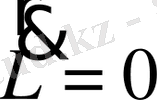 ,
,
бұдан
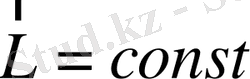 . (1. 7)
. (1. 7)
Бұл тұжырым импульс моментінің сақталу заңы деп аталады. Дербес жағдайда, импульс моментінің сақталу заңы оқшауланған жүйе үшін орындалады. Себебі, оқшауланған жүйе үшін сыртқы күштер моменттері нольге тең болады.
Центрлік күштер маңызды роль атқарады. Бұл жағдайда жүйенің материалды нүктелеріне әсер ететін барлық күштердің бағыттары қозғалмайтын центр О арқылы өтеді. О нүктесіне қатысты осындай күштердің моменті нольге тең. Сондықтан О нүктесіне қатысты жүйенің импульс моменті сақталуы қажет, яғни уақыт бойынша өзгермейді. Бұл жағдай күштер жылдамдыққа тәуелді болса да орындалады[2] .
Импульс пен энергияның сақталу заңдарымен қатар импульс моментінің сақталу заңы физиканың ең маңызды фундаментальды заңы болып табылады. Атомдық физикада импульс моменті ұғымы жалпылануы қажет. Себебі классикалық физикада импульс моменті бөлшектің координатасы және жылдамдығы арқылы анықталады. Ал атомдық физикада Гейзенбергтің анықталмаушылық қатынасына сәйкес бір мезгілде екеуі анықталмайды. Сонымен қатар импульс моментіне бөлшектермен қатар өрістер де ие бола алады, мысалы электромагниттік өрістер. Классикалық механикадағы ұғымдар мен заңдары атомдарға, ядроның ішіндегі бөлшектерге және элементар бөлшектерге қатысты процестерге қолданылады. Сондықтан физикадағы импульс моменті ширек түрде қолданылуы қажет деген ескертумен шектелеміз. Факті түрде оның қолданылуы қалай жүзеге асырылады деген сұраққа әлі дайын емеспіз. Физиканы зерттеуші ең алдымен импульс моментінің механикалық ұғымын жалпылайды және оның сақталу заңын барлық физикалық процесстерге қолданады деп ескеруі қажет.
Механикадағы импульс моментінің сақталу заңын екі материалды нүктелер жүйесіне қолданып, оны негізгі постулат ретінде қарастыруға болады. Онда Ньютонның үшінші заңын механиканың негізгі постулаттарынан алып тастауға мүмкіндік бар. Механика курсында Ньютонның үшінші заңы импульстің сақталу заңының салдары ретінде көрсетіледі. Егер импульстің сақталу заңына импульс моментінің сақталу заңын қоссақ, онда осы екі заңнан Ньютонның үшінші заңын алуға болады. Шындығында, екі материалды нүктеден тұратын тұйық жүйені алайық. Бұл екі нүкте бір-бірімен
 және
және
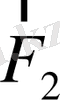 күштермен әсерлесетін болсын. Импульстің сақталу заңынан
күштермен әсерлесетін болсын. Импульстің сақталу заңынан
 екендігі анықталады, ал импульс моментінің сақталу заңынан мынадай теңдеу анықталады:
екендігі анықталады, ал импульс моментінің сақталу заңынан мынадай теңдеу анықталады:
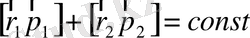 . (1. 8)
. (1. 8)
Осы теңдеуді уақыт бойынша дифференциалдасақ, онда мынадай теңдеу аламыз:
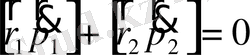 (1. 9)
(1. 9)
немесе
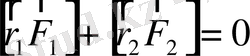 (1. 10)
(1. 10)
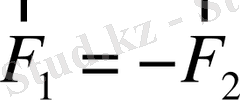 болса, онда
болса, онда
 (1. 11)
(1. 11)
Осыдан
 және
және
 векторлары коллениарлы екендігі анықталады. Олай болса
векторлары коллениарлы екендігі анықталады. Олай болса
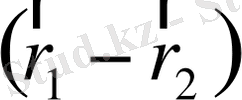 және
және
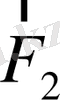 векторлары да коллениарлы екендігі дәлелденеді. Сонда
векторлары да коллениарлы екендігі дәлелденеді. Сонда
 және
және
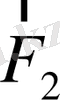 күштері бір түзудің бойында бағытталған, ол түзу екі материалды нүктелерді қосады.
күштері бір түзудің бойында бағытталған, ол түзу екі материалды нүктелерді қосады.
Күштердің моменті және импульстің моменті осы векторлардың модулі мен бағытына ғана байланысты емес, сонымен қатар бастама нүктесіне де (координата басына) байланысты болады. Егер бастама нүктесін орын ауыстыратын болсақ, онда екі момент те өзгереді:
 және
және
 -екі қозғалмайтын бастама нүктелері болсын.
-екі қозғалмайтын бастама нүктелері болсын.
 және
және
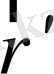 радиус-векторлары арасында
радиус-векторлары арасында
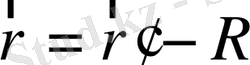 (1. 12)
(1. 12)
байланыс бар. Мұнда
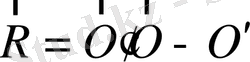 нүктесіне қарасты
нүктесіне қарасты
 нүктесінің радиус-векторы. Жүйенің әрбір нүктесі үшін импульс моменттері өрнегін жазып және олардың қосындысын алсақ, онда мынадай өрнек аламыз.
нүктесінің радиус-векторы. Жүйенің әрбір нүктесі үшін импульс моменттері өрнегін жазып және олардың қосындысын алсақ, онда мынадай өрнек аламыз.
М

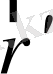
O
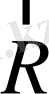
О /
2 - сурет. Күш және импульс моментінің бастама нүктесіне байланыстылығы
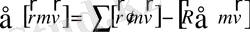 (1. 13)
(1. 13)
немесе
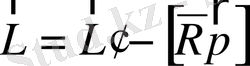 , (1. 14)
, (1. 14)
мұндағы
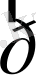 - жүйенің толық импульсі.
- жүйенің толық импульсі.
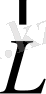 және
және
 -
-
 және
және
 бастамаларына қатысты жүйенің импульс моменттері. Егер
бастамаларына қатысты жүйенің импульс моменттері. Егер
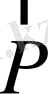 импульс нольге тең болса, онда
импульс нольге тең болса, онда
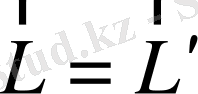 . Бұл жағдайда жүйенің импульс моменті бастама нүктесіне байланысты болмайды. Дәл сол сияқты
. Бұл жағдайда жүйенің импульс моменті бастама нүктесіне байланысты болмайды. Дәл сол сияқты
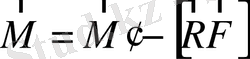 , (1. 15)
, (1. 15)
мұндағы
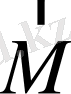 және
және
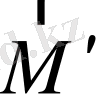 -
-
 және
және
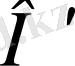 бастамаларына қатысты жүйеге әсер етуші күш моменттері, ал
бастамаларына қатысты жүйеге әсер етуші күш моменттері, ал
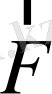 - бұл күштердің геометриялық қосындысы. Егер қорытқы күш
- бұл күштердің геометриялық қосындысы. Егер қорытқы күш
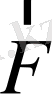 нольге тең болса, онда
нольге тең болса, онда
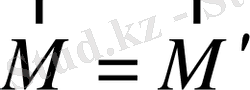 . Бұл жағдай жұп күштер (пара сил) үшін орынды. Жұп күштер туралы айтқан кезде олардың моменті бастама нүктесіне байланысты емес екендігі осыдан шығады.
. Бұл жағдай жұп күштер (пара сил) үшін орынды. Жұп күштер туралы айтқан кезде олардың моменті бастама нүктесіне байланысты емес екендігі осыдан шығады.
1. 2. Қозғалмайтын оське қатысты импульс моменті және күш моменті. Қозғалмайтын осьті айнала қозғалғанда импульс моментінің теңдеуі.
Егер жүйе бір материалды нүктеден тұратын болса, онда оның импульс моментінің қарапайым геометриялық мағынасы бар. Егер t уақыт моментінде материалды нүктенің радиус-векторы
 болсын(3-сурет), dt уақыт ішінде радиус-вектор
болсын(3-сурет), dt уақыт ішінде радиус-вектор
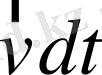 -ға тең өсімше алады да, ол радиус-вектор
-ға тең өсімше алады да, ол радиус-вектор
 кішігірім үшбұрыш сызады. Суретте ол штрихталған үшбұрыш. Бұл үшбұрыштың ауданын мынандай вектор арқылы кескіндеуге болады.
кішігірім үшбұрыш сызады. Суретте ол штрихталған үшбұрыш. Бұл үшбұрыштың ауданын мынандай вектор арқылы кескіндеуге болады.
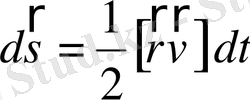 , (1. 16)
, (1. 16)
Бұл вектордың ұзындығы қарастырылып отырған ауданға тең, ал оның бағыты үшбұрыш жазықтығына перпендикуляр.

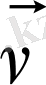 dt
dt

3-сурет. Секторлық жылдамдық және аудандар теоремасы.
Бұл вектордың туындысы
(1. 17)
радиус-вектордың бірлік уақыт ішінде сызатын ауданға тең. Оны секторлық жылдамдық деп атайды. Анықтама бойынша
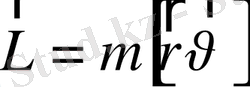 , онда
, онда
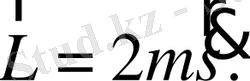 (1. 18)
(1. 18)
Релятивті емес қозғалыста масса
 тұрақты шама, сондықтан импульс моменті
тұрақты шама, сондықтан импульс моменті
 секторлы жылдамдыққа
секторлы жылдамдыққа
 пропорционал[4] .
пропорционал[4] .
Егер материалды нүктеге әсер ететін күш центрлік болса және оның бағыты
О
полюсінен өтетін болса, онда
 векторы уақыт бойынша өзгермейді. Релятивті емес қозғалыс кезінде
векторы уақыт бойынша өзгермейді. Релятивті емес қозғалыс кезінде
 секторлық жылдамдық та өзгермейді. Бұл жағдайда импульс моментінің сақталу заңы аудандар заңына өтеді:
секторлық жылдамдық та өзгермейді. Бұл жағдайда импульс моментінің сақталу заңы аудандар заңына өтеді:
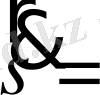 const (1. 19)
const (1. 19)
Бұл теңдеуден екі салдар шығады. Біріншіден,
 және
және
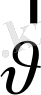 векторлары жататын жазықтық
векторлары жататын жазықтық
 векторына перпендикуляр болады. Ол бағыт тұрақты болғандықтан сол жазықтықта
векторына перпендикуляр болады. Ол бағыт тұрақты болғандықтан сол жазықтықта
 уақыт бойынша өзгермейді. Осыдан мынандай тұжырым жасауға болады: центральды күштер өрісінде материалды нүктенің траекториясы жазықтықтың қисық сызығы болады. Екіншіден,
уақыт бойынша өзгермейді. Осыдан мынандай тұжырым жасауға болады: центральды күштер өрісінде материалды нүктенің траекториясы жазықтықтың қисық сызығы болады. Екіншіден,
 векторының ұзындығы тұрақты болғандықтан әрбір тең уақыт аралығында материалды нүктенің радиус-векторы өлшемі жағынан бірдей аудандар сызады. Бұл қағиданы да аудандар заңы деп атайды. Біз аудандар заңына ширек мағына беруге тырысамыз, яғни аудан өзінің өлшемімен қатар оның кеңістікте бағытымен сипатталады.
векторының ұзындығы тұрақты болғандықтан әрбір тең уақыт аралығында материалды нүктенің радиус-векторы өлшемі жағынан бірдей аудандар сызады. Бұл қағиданы да аудандар заңы деп атайды. Біз аудандар заңына ширек мағына беруге тырысамыз, яғни аудан өзінің өлшемімен қатар оның кеңістікте бағытымен сипатталады.
Осының кері тұжырымы да орынды. Егер материалды нүктенің траекториясы жазықтықтағы қисық сызық және қозғалмайтын бастамадан жүргізілген радиус-вектор бірдей уақыт аралығында бірдей аудан сызатын болса, онда әсер етуші күштің бағыты әрқашанда
О
полюсі арқылы өтеді. Шындығында да секторлық жылдамдық
 тұрақты вектор. Сонда импульс моменті
тұрақты вектор. Сонда импульс моменті
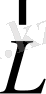 де тұрақты болады. Сондықтан (1. 17) формуласына (заңына) сәйкес
де тұрақты болады. Сондықтан (1. 17) формуласына (заңына) сәйкес
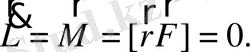

Осыдан
 векторы радиус-векторына
векторы радиус-векторына
 коллинарлы болады, оның бағыты
О
нүктесінен өтеді.
О
нүктесі өріс центрі болып табылады, ол нүктеден тартылу күші немесе тебілу күші материалды нүктеге әсер етеді. Аудандар теоремасы қозғалмайтын өріс центіріне ғана емес, сонымен қатар әртүрлі екі нүктенің біреуіне қатысты орындалады. Екі материалды нүкте бір - бірімен централды күшпен әсерлессін. Келтірілген масса ұғымын қолдана отырып салыстырмалы қозғалысты бір нүктенің екінші қозғалмайтын нүктеге қатысты қозғалысына айналдыруға болады. Ондай күш орталығы ретінде екі нүктенің біреуін алуға болады. Сонда бірінші нүктеден екінші нүктеге жүргізілген радиус-вектор салыстырмалы қозғалыста әрбір тең уақыт аралығында бірдей аудандар сызады.
коллинарлы болады, оның бағыты
О
нүктесінен өтеді.
О
нүктесі өріс центрі болып табылады, ол нүктеден тартылу күші немесе тебілу күші материалды нүктеге әсер етеді. Аудандар теоремасы қозғалмайтын өріс центіріне ғана емес, сонымен қатар әртүрлі екі нүктенің біреуіне қатысты орындалады. Екі материалды нүкте бір - бірімен централды күшпен әсерлессін. Келтірілген масса ұғымын қолдана отырып салыстырмалы қозғалысты бір нүктенің екінші қозғалмайтын нүктеге қатысты қозғалысына айналдыруға болады. Ондай күш орталығы ретінде екі нүктенің біреуін алуға болады. Сонда бірінші нүктеден екінші нүктеге жүргізілген радиус-вектор салыстырмалы қозғалыста әрбір тең уақыт аралығында бірдей аудандар сызады.
Векторлық теңдеу (1. 19) үш скаляр теңдеулерге эквивалентті.
 . (1. 20)
. (1. 20)
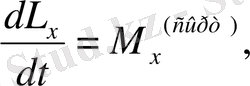
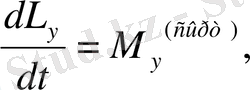
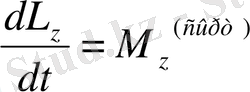 (1. 21)
(1. 21)
Бұл теңдеулер декарттық координата жүйесінің осьтеріне проекцияланғанда алынады. «Сыртқы» деген индекс сыртқы күш моменттерін есептегенде ішкі күштер есепке алынбайды деген мағынаны білдіреді. Сондықтан
 күш моменті кездесетін теңдеулерде ол тек сыртқы күштердің моментін білдіреді.
күш моменті кездесетін теңдеулерде ол тек сыртқы күштердің моментін білдіреді.
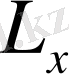 және
және
 X
осьіне қатысты импульс моменті және күш моменті деп аталады. Сол сияқты
У
және
Z
осьтеріне қатысты импульс моменті және күш моменті ретінде айтылады. Жалпы жағдайда
X
осьіне қатысты импульс моменті және күш моменті деп аталады. Сол сияқты
У
және
Z
осьтеріне қатысты импульс моменті және күш моменті ретінде айтылады. Жалпы жағдайда
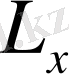 және
және
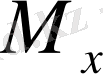 импульс моменті және күш моменті
импульс моменті және күш моменті
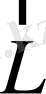 және
және
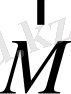 векторларының
X
осіне проекцияларын айтады, ал
О
нүктесі осы қарастырылып отырған осьте жатады. Мына теңдеу
векторларының
X
осіне проекцияларын айтады, ал
О
нүктесі осы қарастырылып отырған осьте жатады. Мына теңдеу
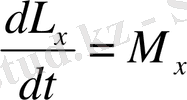 (1. 22)
(1. 22)
қозғалмайтын X осіне қатысты моменттер теңдеуі деп аталады. Егер сыртқы күштің моменті кейбір қозғалмайтын оське қатысты нольге тең болса, онда жүйенің сол оське қатысты импульс моменті тұрақты шама болып қалады. Бұл қозғалмайтын оське қатысты импульс моментінің сақталу заңы.
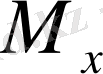 күш моментінің геометриялық мағынасын анықтау үшін
күш моментінің геометриялық мағынасын анықтау үшін
 және
және
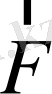 векторларын мына түрде жазайық.
векторларын мына түрде жазайық.
 ,
,
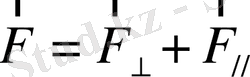 (1. 23)
(1. 23)
Мұндағы
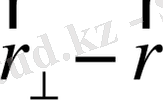 векторының
X
осіне перпендикуляр құраушысы, ал
векторының
X
осіне перпендикуляр құраушысы, ал
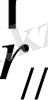 - сол вектордың оське параллель құраушысы. Сол сияқты
- сол вектордың оське параллель құраушысы. Сол сияқты
 және
және
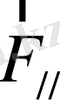 векторларының мағынасы да сондай. Осы жіктеулерді қолданып былай жазуға болады:
векторларының мағынасы да сондай. Осы жіктеулерді қолданып былай жазуға болады:
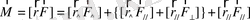 . (1. 24)
. (1. 24)
Соңғы мүше нольге тең, себебі параллель векторлардың векторлық көбейтіндісі
нольге тең. Фигуралы жақшаның ішіндегі қосынды
X
осіне перпендикуляр вектор. Оның
X
осіне проекциясы нольге тең. Сонымен
 вектордың
X
осіне параллель құраушысы
вектордың
X
осіне параллель құраушысы
 (1. 25)
(1. 25)
Осы ғана құраушы
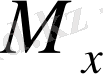 моментінің X осіне қатысты табуда роль атқарады. Сол сияқты
моментінің X осіне қатысты табуда роль атқарады. Сол сияқты
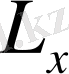 проекциясын табу кезінде де
проекциясын табу кезінде де
 векторының
X
өсіне параллель құраушысын проекцияласақ жеткілікті:
векторының
X
өсіне параллель құраушысын проекцияласақ жеткілікті:
 . (1. 26)
. (1. 26)
Осы айтылғандар жүйеде бірнеше күш болса және бірнеше материалды нүктелер болса да жалпыланады.
Берілген оське қатысты күштің иіні деп ось пен әсер ететін күш сызығы
арасындағы ең аз қашықтықты айтамыз. Сонда осы оське қатысты күштің моменті
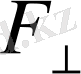 -тің
-тің
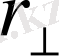 -ге көбейтіндісі ретінде анықталады. Осындай анықтама элементар физикада беріледі. Күштің түсу нүктесін әсер ететін түзу бойымен орын ауыстыруға болатындықтан, бұл анықтама жоғарыда келтірілген анықтамамен сәйкес келеді. Ол 3-суретте келтірілген, мұнда ось сурет жазықтығына перпендикуляр және
О
полюстен өтеді.
-ге көбейтіндісі ретінде анықталады. Осындай анықтама элементар физикада беріледі. Күштің түсу нүктесін әсер ететін түзу бойымен орын ауыстыруға болатындықтан, бұл анықтама жоғарыда келтірілген анықтамамен сәйкес келеді. Ол 3-суретте келтірілген, мұнда ось сурет жазықтығына перпендикуляр және
О
полюстен өтеді.
Дәл осы сияқты материалды нүктенің оське қатысты импульс моменті сәйкес таңбасымен алынған оське перпендикуляр импульс құраушысын
 сәйкес иінге көбейтіндісі
сәйкес иінге көбейтіндісі
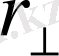 ретінде анықталды.
ретінде анықталды.
Моменттер теңдеуін айналмалы қозғалысқа қолданайық. Қозғалмайтын ось ретінде айналу осін таңдап алуға болады. Егер материалды нүкте шеңбер бойымен қозғалатын болса (4-сурет), онда оның импульс моменті
L = mʋr. (1. 27)
егер ω - бұрыштық жылдамдық болса, онда ϑ = ωr, Сондықтын L = m ω.
Егер О осьті айнала материалды нүктелер жүйесі (бірдей бұрыштық жылдамдықпен) қозғалатын болса, онда
L = m ω, (1. 28)
мұнда қосынды барлық материалды нүктелер бойынша алынады. Тұрақты ω шамасын қосындының алдына шығаруға болады. Сонда
L = Iω, (1. 29)
мұндағы I = Σm . (1. 30)
I шамасы жүйенің берілген оське қарасты инерция моментті деп аталады. (1. 30) теңдеуі жүйе берілген оське қатысты айналған кезде оның импульс моменті инерция моментін бұрыштық жылдымдыққа көбейтіндісіне тең екендігін көрсетеді[5] .

m
4 - сурет 5-сурет. Берілген оське қатысты
Қозғалмайтын оське қатысты күштің иіні
импульс моменті
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz