Жиындар мен математикалық логика: нақты сандар және функциялар теориясы


Жиындар мен математикалық логика элементтері. Нақты сандар және олардың қасиеттері. Бірінің ішінде бірі кесінділер қағидасы. Жиындар. Жиындарға қолданылатын амалдар. Функциялар. Функцияларды композиция-сы(бейнелеу), Элементар функциялар. Функция графигі, кері функция.
Математика пәні кісілік қоғамында ерекше орын алады. Басқа табиғи пәндер үшін түрлі табиғи құбылыстар арасындағы қатыстарды зерттейді. Табиғи құбылыстардың моделін жасайды, және олардың элементтері арасындағы байланысты зерттейді. Бұның үшін тұрақты және айнымалы шамаларды қолданады. Кемінде екі түрлі мәнді қабылдайтын шамаға айнымалы шама делінеді. Айнымалы шамаларды x, y, z, t… лармен ал тұрақты шамаларды a, b, c, d, …лармен белгілеу қабылданған. Айнымалы шаманың мәндері тобына шаманың мәндері жиындысы делінеді. Жиындар бас әріптермен белгіленеді. Мысал. а ∈ А жазуы а А жиынның элементі екендігін ал а ∉ А жазуы а А жиынның элементі емес екендігін білдіреді. А жиынның элементтері А={a 1 , a 2, …, a n }={a n } мен белгіленеді. А жиыны негізгі U жиынының d қасиетіне ие болатын элементтерінің жиынтығы ретінде берілсе ол А ={x∈U:d(x) } арқылы белгіленеді.
Мысал.
А={x∈N:x≥100}={100, 101, 102, …} < A={1, 2, 3, 5, 7, 10}, B={4, 5, 8, 10, 12} болса
A={ x∈N: (x 2 -4x+3) =0}= {1, 3}
A+B ға А және В жиындардың бірігуі деп аталады ол А ∪ В арқылы белгіленеді. A*В А және В жиындыларының қиылысуы деп аталады ол А∩ В арқылы белгіленеді.
Мысал. А={1, 235, 7, 10} В={4, 5, 8, 10, 12} болса А ∪ В = {1, 2, 3, 4, 5, 6, 9, 10, 12};
A={1, 2, 3, 4, 5}, B={3, 4, 5, 6, 7} болса А ∩ В= {4, 5}
Бірігу және қиылысу төмендегі қасиеттерге ие.
1. А ∪ В = B ∪ A, A ∩ B = B ∩ A коммутативтік қасиеті
2. A∪ (B∪C) = (A ∪B) ∪C, A ∩( B ∩ C) = (A ∩ B) ∩C ассоциативтік қасиеті
3. A∪ (B∩C) = (A ∩ C) ∪(B∩C) дистрибутивтік қасиеті
(A ∩ B) ∪C=( A ∪C) ∩ (B∪C)
А∪∅=A А∩∅=∅ (∅ бос топ)
А∩В=∅ болса А және В қиылыспайтын жиындар
A \ B немесе А-В - А жиынының В Жиынына тиісті болмаған элементтеріне айтылады.
Мысал. C = A\B={x∈A:x∉B}
A={1, 2, 5, 7}, B={3, 5, 9} болса, C={1, 2, 7} болады.
А жиынының толықтауышы
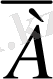 Equation. 3 мен белгіленеді. Сонда
Equation. 3 мен белгіленеді. Сонда
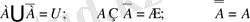 болады.
болады.
Енді негізгі сандар жиыннын атап өтейік.
- {1, 2, 3, …}=Nнатуралсандар жиыны.
Натурал сандар жиынында қосу және көбейту амалдары үнемі орындалады.
2. {…, -2, -1, 0, 1, 2, …} =Z бүтін сандар жиыны.
Бүтін сандар жиынында қосу, алу және көбейту амалдары үнемі орындалады.
3.
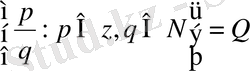 сандар рационал сандар жиыны деп аталады.
сандар рационал сандар жиыны деп аталады.
Рационал сандар жиынында қосу, алу, көбейту және бөлу амалдары орындалады. (математикада нөлге бөлу амалы жоқ)
4. Рационал болмаған сандар жиыны иррационал сандар жиыны деп аталады.
Мысал: π≈3, 1415 . . . е ≈ 2, 7182818284 . . . ,
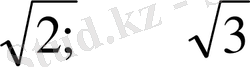 , . . .
, . . .
5. Рационал және иррационал сандар тобы нақты сандар жиыны деп аталады. Ол R мен белгіленеді. Нақты сандар мен Ох өсі нүктклері арасында бір мәнді сәйкестік орнатылған.
Нақты сандар жиынында қосу, алу, көбейту, бөлу, дәрежеге көтеру және оң сандарға түбір шығару амалдары орындалады.
Кейбір математикалық логика символдары.
1. α⇒β жазуы α дан β келіп шығады дегенді білдіреді. ⇒ - имплекация символы.
2. α⇔β α дан β, және β дан α келіп шығады дегенді білдіреді, яғни α=β. ⇔
 - пара -пар символы.
- пара -пар символы.
3. α∧β α және β дегенді білдіреді. ∩ - коньюнкция символы.
4. α∨β α немесе β дегенді білдіреді. ∨ - дизьюнгция символы.
- ∀х∈Х:α(х) Х жиынының кез келген х элементі үшін α(х) қасиеті орындалады дегенді білдіреді. ∀Ағылшын Any-барлық сөзінің бірінші әріпінің төңкеріліп жазылуы.
- ∃ х∈Х: α(х) Х жиынында α(х) қасиетке ие болған х элементтері бар дегенді білдіреді. ∃ Ағылшын Existens-бар деген сөзінің бірінші әріпінің теріс жазылуы. Х та α(х) шартына ие болған тек қана бір х бар болса ∃! х∈х: α(х) арқылы жазылады.
Кесінді, аралық және шенелген жиын.
[а, в]
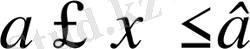 теңсіздікті қанағаттандырушы х сандар жиынына кесінді немесе сегмент делінеді.
теңсіздікті қанағаттандырушы х сандар жиынына кесінді немесе сегмент делінеді.
(а, в) - a<x<в теңсіздікті қанағаттандырушы х сандар жиынына интервал делінеді.
[а, в) немесе (а, в] белгілері жартылай сегмент деп аталады.
Кеңейтірілген сандар өрісінде а санының ε маңайы Оε(а) арқылы белгіленед Оε(а) =(a- ε, a+ ε) ={x∈R:
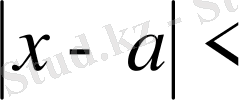 ε}
ε}
X жиынының
 үшін
үшін
 шарты орындалса Х жоғарыдан, ал
шарты орындалса Х жоғарыдан, ал
 шарты орындалса Х төменнен шенелген делінеді.
шарты орындалса Х төменнен шенелген делінеді.
Функция анықтамасы. Функцияның берілу тәсілдері
Анықтама. Егер қарастырылып отырған айнымала шама Х-тің әрбір мәніне белгілі заң немесе ереже бойынша айнымалы шама у-тің анықталған бірақ мәні сәйкес келіп отырса, айнымалы шама у айнымалы шама х-тің функциясы деп аталады. Мұндағы х - тәуелсіз айнымалы немесе аргумент , ал у - тәуелді айнымалы немесе функция деп аталады.
Анықтама. Егер тәуелсіз айнымалы х- тің әрбір мәніне белгілі заң немесе ереже бойынша тәуелді айнымалы у-тің бірнеше мәндері сәйкес келетін болса, ондай айнымалы у- көп мәнді функция деп аталады.
Функция берілген деп саналады, егер: біріншіден, аргументтің қарастырылатын мәндерінің жиыны көрсетілген болса; екіншіден, аргумент х- тің берілген мәні бойынша функция у-тің сәйкес мәнін табуға мүмкіндік беретін сәйкестік заң көрсетілген болса.
Функцияның белгіленуі: y=f(x) , y=φ(x),
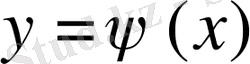 , y=F(x)
, y=F(x)
Оқылуы: игрек икстен эфке тең, игрек икстен фиге тең.
Мұндағы f, φ, ψ, F- аргумент х- тің берілген мәні бойынша у-тің сәйкес мәні қалай табылатынын көрсететін заңды немесе ережені бейнелейді.
Функция ұғымы бүкіл математика үшін өте маңызы зор ұғым, сондықтан да, ол ұғым математикалық дамудың ең негізгі обектісі болып саналады.
Анықтама . Функция анықталған немесе ақырлы нақты мәндер қабылдайтын тәуелсіз айнымалының барлық мәндерінің жиыны сол функицяның анықталу облысы немесе функцияның бар болу облысы деп аталады, ал функцияның барлық мәндерінің жиыны функция мәндерінің жиыны деп аталады.
Мысалы:
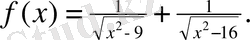 анықталу облысын табу керек.
анықталу облысын табу керек.
Шешуі. Қарастырылып отырған f(х) функциясының мәндері аргумент х-тің мәндері мына екі теңсіздікті бір кезде қанағаттандырғанда ғана нақты сандар бола алады.
х² - 9>0 х²- 16>0
│х│>3 │х│>4
Функицяның анықталу облысы │х│>4 теңсіздігін қанағаттандыратын х-тің барлық мәндерінің жиыны болады, яғни (-∞; -4) (4; +∞)

2)
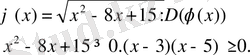
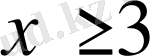 және
және
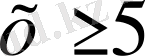
3) φ(х) =
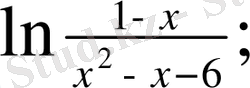 Equation. 3 D-?
Equation. 3 D-?
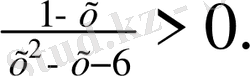
а) 1-х >0 х²-х-6>0 б) 1-х< 0 х²-х-6<0
1-х>0 (х+2) (х-3) >0 1-х<0 (х+2) (х-3) <0
-х>-1 х<-2 х>3. х>1 -2<х<3 (1; 3)
х< 1 (-∞:-2)
 1<х<3
1<х<3
4) g(x) = ln (1-2cosx) D (g) -?
1-2cosx>0
cosx <
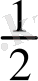 Equation. 3,
Equation. 3,
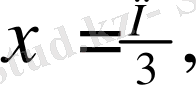 Equation. 3
Equation. 3
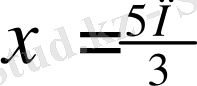 Equation. 3 те cosx =
Equation. 3 те cosx =
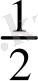 ; сонымен,
; сонымен,
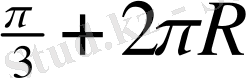 <х<
<х<
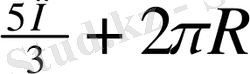 ,
,
R=0, 1, 2, . . .
5)
 D(h) -?.
D(h) -?.
-
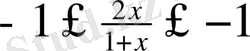 Equation. 3,
Equation. 3,
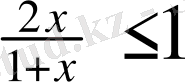 Equation. 3,
Equation. 3,
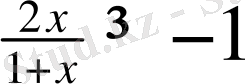 Equation. 3,
Equation. 3,
2x≤1+x 2x≥-1-x
x≤1 2x+x>-1
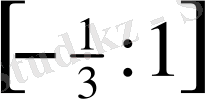 Equation. 3
Equation. 3
3x≥-1
x≥-
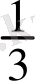
- F(x) =
-1
-1≤sinx≤1, ендеше -1<
<1- орындалмайды.
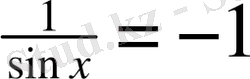
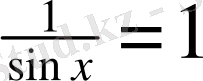
.
Функцияның графигі.
(а, в) аралығында анықталған у=f(x) функциясы берілген делік. Ол дегеніміз (а, в) аралығындағы х-тің әрбір мәніне у-тің анықталған біріңғай мәні сәйкес келеді.
Жазықтықтағы тік бұрышты координаталар системасын алалық. N нүктесі (а, в) аралығындағы абщиссасы х - ке тең нүкте болсын. Абсциссалар өсіне N нүктесі арқылы өтетін перпендикуляр тұрғызайық. Сонда абсциссасы х-ке тең, оған сәйкес кординатасы f(x) ке тең болатын М нүктесі тұрғызылған перпендикулярдың бойынша орналасады және ондай нүкте жалғыз болады. Сонымен ON=x, NM=y=f(x) . NM кесіндісінің М нүктесін х-тің берілген мәніне сәйкес келетін f(x) тің мәнінің геометриялық кескіні деп санаймыз. Осылайша берілген функцияның геометриялық кескінін сала аламыз. Ол кескін аргументтің қабылдайтын барлық мәндеріне сәйкес функцияның барлық мәндерін кескіндейтін нүктелердің геометриялық орны болады.
Қозғалмалы М нүктесі жасаған бұл геометриялық орын f(x) функциясының графигі деп аталады.
Сонымен, абсциссалары - аргументтік мәндері, кординаталары - функцияның мәндері болатын жазықтықтағы нүктелердің жиыны функцияның графигі деп аталады.
Функцияның графигтері қисық сызықтар немесе түзулер болады.
Функцияның графигін салу үшін, ол функцияның аргументінің бірнеше мәндерін алып, оған сәйкес функцияның мәндерін тауып таблица құру керек.
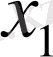
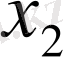
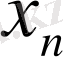
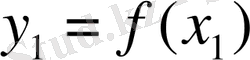
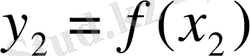
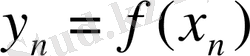
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz