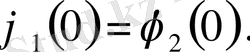Екінші ретті дербес туындылы теңдеулер: классификация, канондық түрлері және шешу әдістері


Дербес туындылы дифференциалдық теңдеулер классификациясы
§ 1. Екінші ретті теңдеулер классификациясы
- Екінші ретті теңдеулердің берілуі
- Түрлендірулер
- Характеристикалық теңдеу
- Теңдеулердің түрлері
- Екі айнымалылы дифференциалдық теңдеулер.
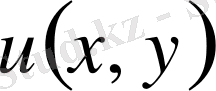 :
:
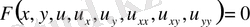 -
екінші ретті дербес туындылы теңдеу
деп аталады.
-
екінші ретті дербес туындылы теңдеу
деп аталады.
Бұл теңдеу жоғарғы ретті туындылары бойынша сызықтық деп аталады, егер мына түрде жазылса:
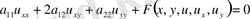 (1)
(1)
Мұндағы
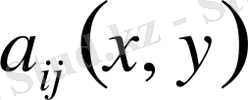 теңдеудің коэффициенттері. Егер осы (1) теңдеудің коэффициенттері
теңдеудің коэффициенттері. Егер осы (1) теңдеудің коэффициенттері
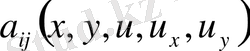 тәуелді болса, онда бұл теңдеу
квазисызықтық
деп аталады. Теңдеу сызықтық делінеді, егер мына түрде берілсе:
тәуелді болса, онда бұл теңдеу
квазисызықтық
деп аталады. Теңдеу сызықтық делінеді, егер мына түрде берілсе:
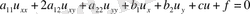 (2)
(2)
(2) теңдеу
сызықтық
деп аталады.
 -
коэффициенттері тұрақты болған жағдайда теңдеу
тұрақты коэффициентті
делінеді. Егер
-
коэффициенттері тұрақты болған жағдайда теңдеу
тұрақты коэффициентті
делінеді. Егер
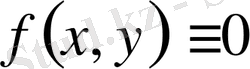 болса, онда (2) теңдеу
сызықтық біртекті
делінеді. Ал егер ол нольге тең болмаса, яғни
болса, онда (2) теңдеу
сызықтық біртекті
делінеді. Ал егер ол нольге тең болмаса, яғни
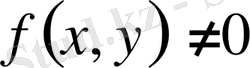 болса, онда ол
сызықты біртекті емес
деп аталады.
болса, онда ол
сызықты біртекті емес
деп аталады.
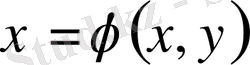 ,
,
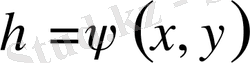 түрлендірулердің көмегімен теңдеуді жай түрде келтіреді.
түрлендірулердің көмегімен теңдеуді жай түрде келтіреді.
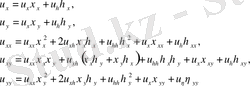 (3)
(3)
түрлендіру нәтижесінде мына түрге келтіреміз.
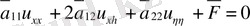 (4)
(4)
мұндағы
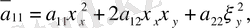
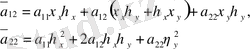
Егер бастапқы (1) теңдеу сызықтық болса, яғни
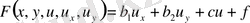 болса. Онда түрлендіру нәтижесінде
болса. Онда түрлендіру нәтижесінде
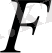 мына түрде жүреді.
мына түрде жүреді.
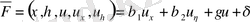
 және
және
 -ны
-ны
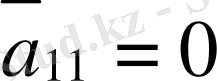 етіп таңдаймыз. Осыған байланысты
етіп таңдаймыз. Осыған байланысты
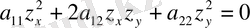 (5)
(5)
теңдеуі қарастырылады.
Бұл теңдеуге байланысты леммалар.
Лемма
1.
Егер
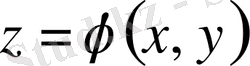 (5) теңдеудің дербес шешімі болса. Онда
(5) теңдеудің дербес шешімі болса. Онда
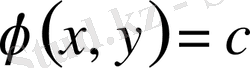 функциясы
функциясы
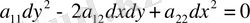 (6)
(6)
теңдеуінің жалпы шешімі.
Лемма
2.
Егер
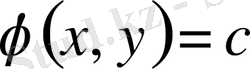 (6) теңдеудің жалпы шешімі болса, онда
(6) теңдеудің жалпы шешімі болса, онда
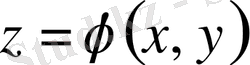 функциясы (5) теңдеуді қанағаттандырады.
функциясы (5) теңдеуді қанағаттандырады.
(6) теңдеу (1) теңдеудің характеристикалық теңдеуі делінеді, ал бұл (6) теңдеудің интегралдары (1) теңдеудің характеристикалары деп аталады.
1. Лемманы дәлелдеу:
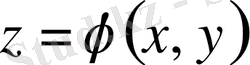 (5) теңдеудің шешімі
(5) теңдеудің шешімі
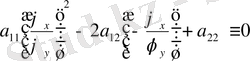 (7)
(7)
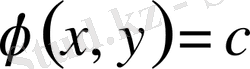 айқын белгілеген функцияны мына түрде жазуға болады.
айқын белгілеген функцияны мына түрде жазуға болады.
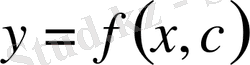 , онда
, онда
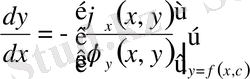 (8)
(8)
онда біз мынаны жазамыз.

Лемма дәлелденді. Характеристикалық теңдеу
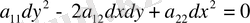
бұл теңдеуді мына түрге келтіреміз.
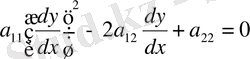
онда бұл теңдеудің екі шешімі бар.
1)
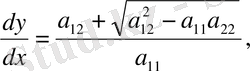 (9)
(9)
2)
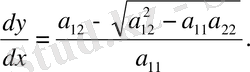 (10)
(10)
Сонымен
 нүктесінде біз мынадай анықтау қосамыз.
нүктесінде біз мынадай анықтау қосамыз.
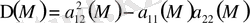
1.
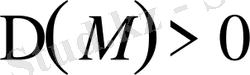 , онда дифференциалдық теңдеу
гиперболалық тектес
, себебі бұлардың екі нақты шешім шығады.
, онда дифференциалдық теңдеу
гиперболалық тектес
, себебі бұлардың екі нақты шешім шығады.
2.
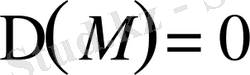 , онда дифференциалдық теңдеу
параболалық тектес.
, онда дифференциалдық теңдеу
параболалық тектес.
3.
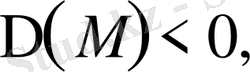 онда дифференциалдық теңдеу
эллиптикалық тектес
.
онда дифференциалдық теңдеу
эллиптикалық тектес
.
Егер жазықтықтың белгілі бір облысы қарастырылатын болса, онда әртүрлі нүктелерінде әртүрлі тектес теңдеулер болуы мүмкін немесе бір ғана тектес теңдеу болуы мүмкін. Облыстың әрбір нүктесінде бір ғана тектес теңдеу болса, онда осы облыста теңдеу сол түрде аталады.
- Гиперболалық тектес.
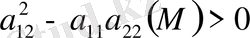 , онда характеристикалық теңдеудің екі жалпы шешімі болады.
, онда характеристикалық теңдеудің екі жалпы шешімі болады.
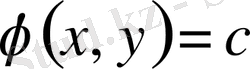 ,
,
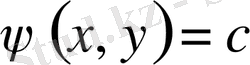 .
.
Енді мынадай алмастырулар жасаймыз.
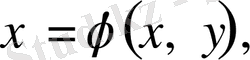
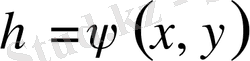 .
.
Сонда теңдеу мына түрге келтіріледі:
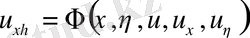
гипербола тектес теңдеудің жай түрі немесе канондық түрі.
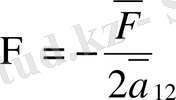
Практикада келесі түрдегі канондық теңдеулер де қолданылады. Алмастырулар жасаймыз.
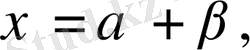
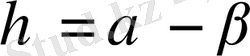 ,
,
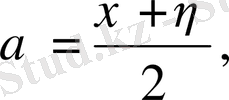
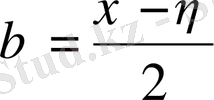
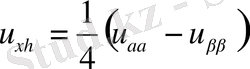 ,
,
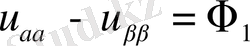
Екінші канондық түрі
 .
.
- Параболалық тектес.
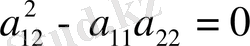 . Шешімі біреу-ақ болады.
. Шешімі біреу-ақ болады.
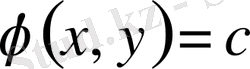 . Енді алмастыру жасаймыз.
. Енді алмастыру жасаймыз.
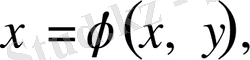
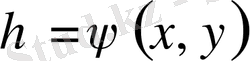 . Мұндағы
. Мұндағы
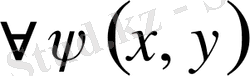
 -мен сызықты тәуелсіз функция.
-мен сызықты тәуелсіз функция.
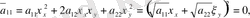
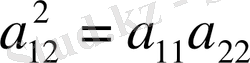
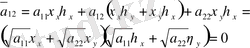
Сонымен бізде мынадай теңдеу шығады.
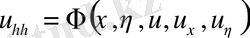 - Парабола тектес теңдеудің канондық түрі.
- Парабола тектес теңдеудің канондық түрі.
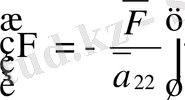
- Элиптикалық тектес.
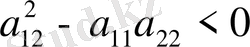 , бұдан, яғни характеристикалық теңдеуден комплекс түйіндес түбірлер шығады.
, бұдан, яғни характеристикалық теңдеуден комплекс түйіндес түбірлер шығады.
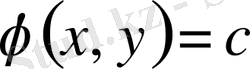 ,
,
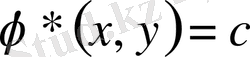 .
.
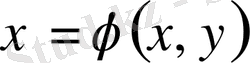 ,
,
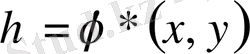 алмастырулар орындалады. Комплекс түйіндестен құтылу үшін келесі түрлендірулер жасаймыз.
алмастырулар орындалады. Комплекс түйіндестен құтылу үшін келесі түрлендірулер жасаймыз.
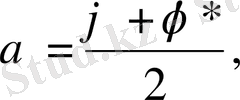
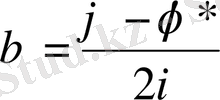
онда
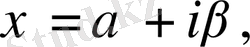
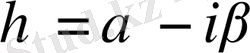 десек, онда біз мынадай теңдеу аламыз.
десек, онда біз мынадай теңдеу аламыз.
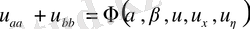 -Элиптикалық тектес теңдеудің жай түрі.
-Элиптикалық тектес теңдеудің жай түрі.
Қорытынды:
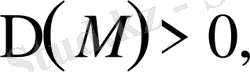
 гипербола тектес.
гипербола тектес.
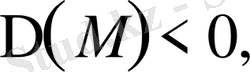
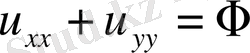 элиптикалық тектес.
элиптикалық тектес.
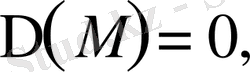
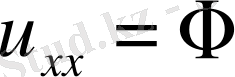 параболалық тектес.
параболалық тектес.
2. Көп айнымалылы екінші ретті теңдеу классификациясы
Сонымен біз мына теңдеуді қарастырамыз.
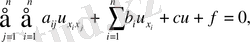 (11)
(11)


Екі айнымалыдан тәуелді жағдайдағыдай зерттеулер нәтижесінде мынадай жай түрдегі теңдеулерді аламыз.
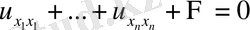 элипс тектес.
элипс тектес.
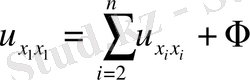 гипербола тектес.
гипербола тектес.
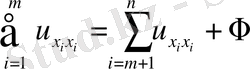 ,
,
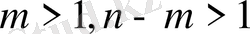 Бұл ультра гипербола тектес.
Бұл ультра гипербола тектес.
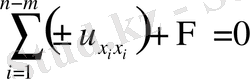 ,
,
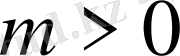 параболалық тектес.
параболалық тектес.
3. Тұрақты коэффициентті теңдеулердің канондық түрлері.
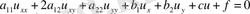 , мұндағы
, мұндағы
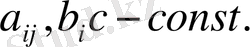
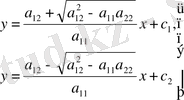 характеристикалық түзулер
характеристикалық түзулер
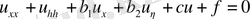 , элипс тектес
, элипс тектес
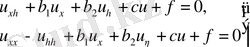 гиперболалық тектес.
гиперболалық тектес.
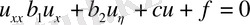 параболалық тектес.
параболалық тектес.
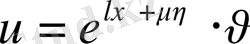 алмастыруын жасаймыз, сонда теңдеу мына түрге келеді.
алмастыруын жасаймыз, сонда теңдеу мына түрге келеді.
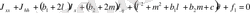
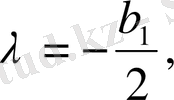
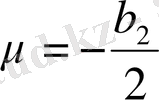 .
.
Сонда теңдеу мына түрге келеді.
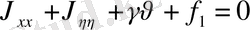 . Мұндағы
. Мұндағы
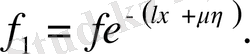
Осы сияқты түрлі комбинациялар арқылы келесі түрдегі теңдеулерді аламыз.
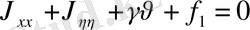 элипс тектес.
элипс тектес.
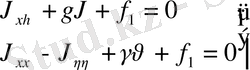 гипербола тектес
гипербола тектес
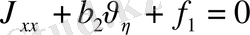 парабола тектес.
парабола тектес.
Тарау ІІ
Гипербола тектес теңдеулер.
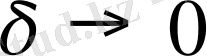
Тербеліс процестері гипербола тектес теңдеулерге келтіріледі. Ең қарапайым түрдегі теңдеуі мынау:
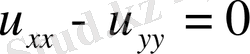 -
шектің тербліс теңдеуі
деп аталады.
-
шектің тербліс теңдеуі
деп аталады.
§ 1. Гипербола тектес теңдеулерге келтірілетін жай есептер. Шеттік есептердің құрылуы.
- Тербеліс процестерінің модельдері.
- Негізгі түсініктер.
- Бастапқы шарттармен қойылған есептер.
- Шекаралық шарттардың түрлері.
- Шеттік есептердің түрлері.
1. Ішектің көлденең жай тербелісінің теңдеуі.
Иілуге икемді серпімді денені ішек деп түсінеміз. Ішектің қозғалысын әрбір нүктесінің қозғалысымен байланыстырып қарауға болады. Бір күйден екінші күйге көшуін вектор арқылы анықтауға болады.
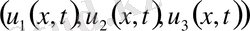
Егер ішек бір жазықтықта тербелетін болса, оны
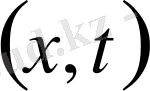 х нүктесіндегі t моментіндегі нүктесін
х нүктесіндегі t моментіндегі нүктесін
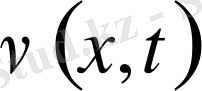 функциясымен анықтай аламыз. Сонымен ішектің әрбір нүктесінің орнын мына вектормен анықтауға болады, егер ол бір жазықтықта тербелсе
функциясымен анықтай аламыз. Сонымен ішектің әрбір нүктесінің орнын мына вектормен анықтауға болады, егер ол бір жазықтықта тербелсе
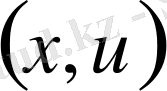
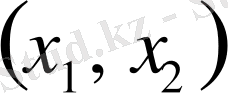 аралығында
аралығында
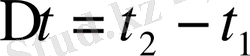 моментінде біз мынадай күштердің
моментінде біз мынадай күштердің
 осіне проекцияларын қарастырамыз.
осіне проекцияларын қарастырамыз.
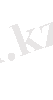 Энерция күші
Энерция күші
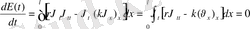
 тартылыс күші
тартылыс күші
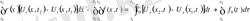 (1)
(1)
тербеліс кезіндегі күштердің тепе- теңі.
теңдеу шектің
 бөлігінің
бөлігінің
 уақыт аралығындағы интегралдық түрдегі тербеліс теңдеуі. Әрбір нүктесінің тербеліс теңдеуін қорыту үшін интегралдық теңдеуден дифференциалдық теңдеуге көшу керек. Ол үшін (1) теңдеуде интегралдық орта мәні туралы теореманы және ақырлы өсімше туралы теореманы қолданамыз.
уақыт аралығындағы интегралдық түрдегі тербеліс теңдеуі. Әрбір нүктесінің тербеліс теңдеуін қорыту үшін интегралдық теңдеуден дифференциалдық теңдеуге көшу керек. Ол үшін (1) теңдеуде интегралдық орта мәні туралы теореманы және ақырлы өсімше туралы теореманы қолданамыз.
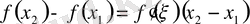
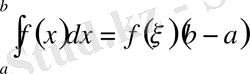
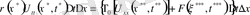

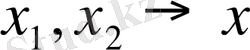 ,
,
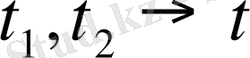
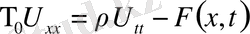 (2)
(2)
(2) Шектің дифференциялдық түрдегі тербеліс теңдеуі.
 (3)
(3)
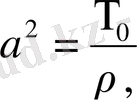
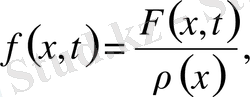
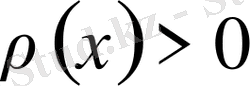
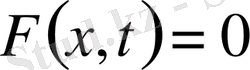
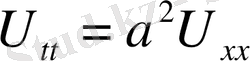 (4)
(4)
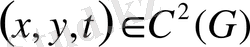
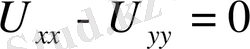 (5)
(5)
Мұндай әсер еткіш күштің нәтижесінде қосымша шартар қойылады. Бұл шарттар мына түрде жазылады.
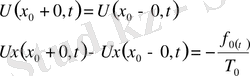 (6)
(6)
Бұл шоғырланған күш әсер ететін нүктедегі түйіндестік шарт деп аталады.
2. Мембраналық тербеліс теңдеуі.
Мембраналық теңдеу мына түрде жазылады.
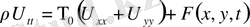 (7)
(7)
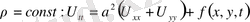 (8)
(8)
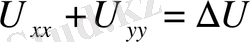 ,
,
 Лаплас операторы
Лаплас операторы
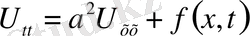

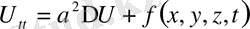 (9)
(9)
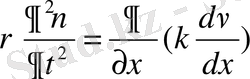
Дифференциялдық теңдеудің шексіз көп шешімі болады.
3. Шекаралық және бастапқы шарттар.
Физикалық процес айқын болуы үшін қосымша шарттар қойылады. Дифференциялдық теңдеу берген қосымша шарттар шекаралық және бастапқы болып бөлінеді. Шекаралық шарттар функцияның анықталу облысына байланысты. Бастапқы шарттар үдерістің басталу облысына байланысты.
Шекті ұзындығының е деп белгілеген
 нүктесінде мына шарт
нүктесінде мына шарт
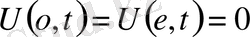 қойылады.
қойылады.
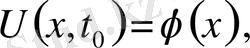
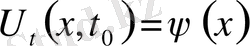 (10)
(10)
Егер шектің екінші шеті тербелісте болатын болса, онда шекаралық шарттар былай болады.
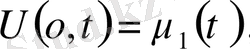
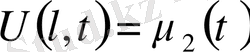
Тербелістегі дененің бір ұшы бекітіліп екінші ұшы бекітілмеген болса, онда мынадай шарттар қойылуы мүмкін.

Екінші ұшы тербелісте болады.
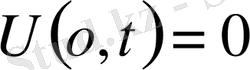 ,
,
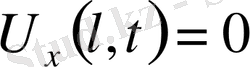 (13)
(13)
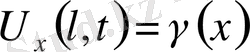
Егер
 нүктесі бекітіліп екінші шеті бекітілмеген жағдайда басқа түрде шекаралық шарттар қойылуы мүмкін. Мына түрдеде қойылуы мүмкін.
нүктесі бекітіліп екінші шеті бекітілмеген жағдайда басқа түрде шекаралық шарттар қойылуы мүмкін. Мына түрдеде қойылуы мүмкін.
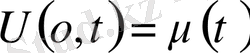
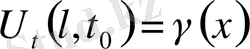 (14)
(14)
Дәл осы сияқты серпімді бекітілген денелерден
 ұшында мынадай шарттар қойылуы мүмкін.
ұшында мынадай шарттар қойылуы мүмкін.
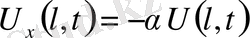 немесе
немесе
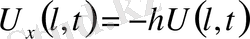 (15)
(15)
Кейде мынадай шарттар койылуы мүмкін.
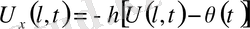 (16)
(16)
Негізінен 3 түрлі шекаралық шарттар қойылады. Шеткі нүктеде функцияның мәні берілсе, онда бұны бірінші шекаралық шарт деп аталады.
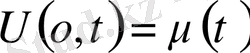 бірінші шекаралық шек. Берілген режим. Ал енді шеткі туындының мәні беріледі.
бірінші шекаралық шек. Берілген режим. Ал енді шеткі туындының мәні беріледі.
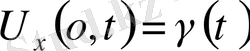 екінші шекаралық шек
. Берілген күш. Мынадай шарт қойылуы мүмкін.
екінші шекаралық шек
. Берілген күш. Мынадай шарт қойылуы мүмкін.
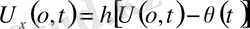 Үшінші шекаралық шек. Серпімді бекіту.
Үшінші шекаралық шек. Серпімді бекіту.
Негізгі шекаралық шарттар және бастапқы шарттар көмегімен 6 түрлі шекаралық есептер қарастырылады. Бұл шекаралық есептерді әдетте шеттік есептер деп аталады. Шекаралық шарттармен байланысты 3 түрлі шеттік есеп бар.
Бірінші шекаралық есеп
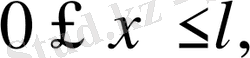
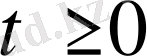 мына облыс анықталған
мына облыс анықталған
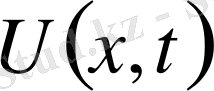 функциясын табу керек. Бұл функция (1)
функциясын табу керек. Бұл функция (1)
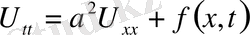 теңдеуі
теңдеуі
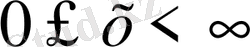
 мыны облысты қанағаттандыру керек және мына шарттарды
мыны облысты қанағаттандыру керек және мына шарттарды
(2)
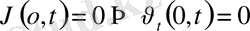 ,
,
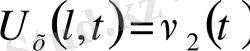
(3)
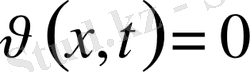 ,
,
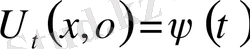 Бірінші шектік есеп
Бірінші шектік есеп
(1) теңдеуді қанағаттандыратын және (3) шартты қанағаттандыратын есеп қойылса екінші шектік есеп деуміз.
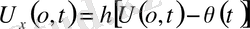
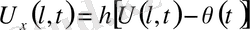
Бұларға басқа шекаралық шарттары аралас түрде қойылған есептерде кездеседі. Егер шекті нүктелердегі құбылыстар ескерілмейтін болса, нода бастапқы шартпен ғана қойылған есепті қарастырамыз.
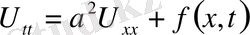 ,
,

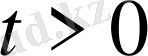
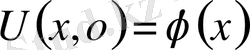 ,
,
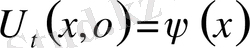 Коши есебі.
Коши есебі.
Дәл осылайша жартылау шектеулі облыстар есептеуде қарастырады.
Мысал:
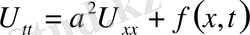 ,
,
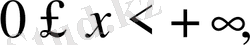

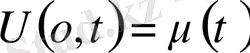
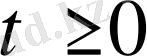
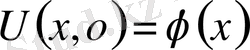 ,
,
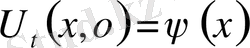 жарты түзу есебі.
жарты түзу есебі.
Егер процесс қай уақытта басталғаны белгісіз болса, нода бастапқы шарттарсыз есептер қойылады.
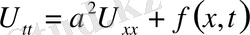 ,
,
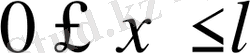
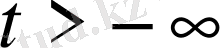
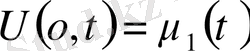 ,
,

4. Жалпы есептің құрылуы (редукциясы) .
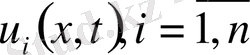 функциясы мына теңдеулерді қанағаттандыатын болсын.
функциясы мына теңдеулерді қанағаттандыатын болсын.
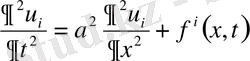 (17)
(17)
шешімдер береді. Ол
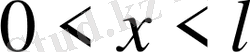 аралығында болады. Сондай-ақ бұл шешімдер қосымша шарттарды қанағаттандыратын болсын:
аралығында болады. Сондай-ақ бұл шешімдер қосымша шарттарды қанағаттандыратын болсын:
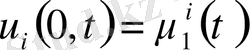
 (18)
(18)
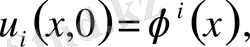
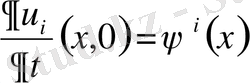
Егер мынадай теңдеу қарастырсақ:
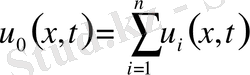 (19)
(19)
Бұл функция келесі есептің шешімін береді.
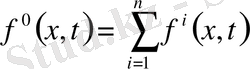 (20)
(20)
Ал қосымша шарттар
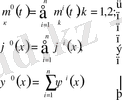 (21)
(21)
(19) теңдеуді алсақ, онда есеіміз мына түрде жазылады.
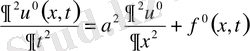
Бұл (20), (21) шарттарын қанағаттандырады. Демек, күрделі есептің шешімін бірнеше жай есептепдің шешімдерінің қосындысы түрінде іздестіруге болады.
Мысалы:
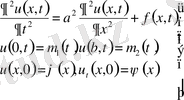 (22)
(22)
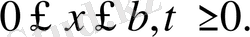
Яғни жалпы түрде қойылған бірінші шеттік есеп берілсе, онда бұл есепті бірнеше есепке бөлшектей аламыз. Ол үшін бұл есептің шешімін мынадай шешімдердің қосындысы түрінде іздестіреміз.
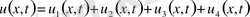 (23)
(23)
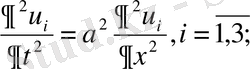
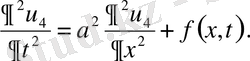
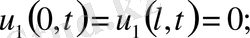 деп аламыз. Ал бастапқы шарты
деп аламыз. Ал бастапқы шарты
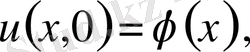
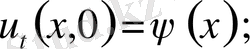
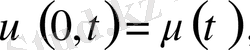
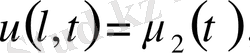
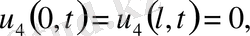
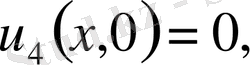
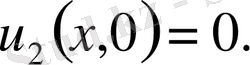
5. Жалғыз шешім теоремасы. (Бір ған шешім теоремасы) .
Теорема:
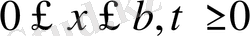 облыста
облыста
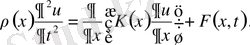
Мұндағы
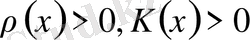
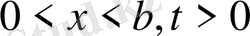 ашық облыста бастапқы шарттары:
ашық облыста бастапқы шарттары:
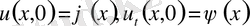 және шекаралық шарттарды
және шекаралық шарттарды
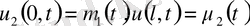
қанағаттандыратын жалғыз шешімі бар, егер
1.
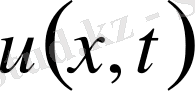 функциясы және оның барлық туындылары
функциясы және оның барлық туындылары
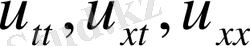
 облыста үзіліссіз болса.
облыста үзіліссіз болса.
2.
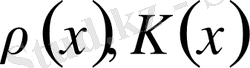 функциялары, яғни коэффициенттер
функциялары, яғни коэффициенттер
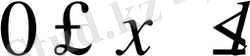 аралығында үзіліссіз болса.
аралығында үзіліссіз болса.
Дәлелдеуі:
кері жориық, яғни екі шешімі бар делік.
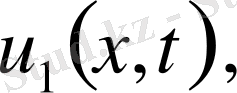
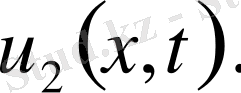
Айырымын қарастырамыз.
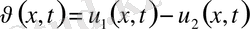 . Бұл біртекті теңдеудің шешімін береді.
. Бұл біртекті теңдеудің шешімін береді.
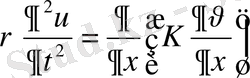 .
.
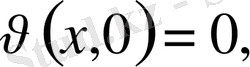
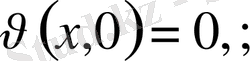
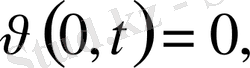
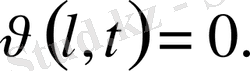
Енді мынадай функция құрамыз.
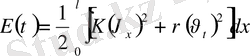 .
.
Бұл функция қозғалыстың толық энергиясын береді. Интеграл астындағы дифференциалдауға көшіп және шектік бастапқы шарттарды ескере отырып,
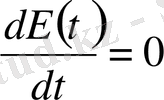
екеніне көз жеткіземіз. Сонда
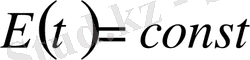 . Ал бұдан
. Ал бұдан
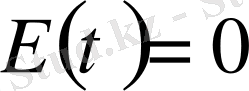 айналатынына көз жеткіземіз. Сондықтан
айналатынына көз жеткіземіз. Сондықтан
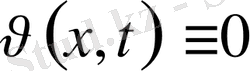 . Яғни,
. Яғни,
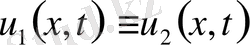 . Теорема дәлелденді.
. Теорема дәлелденді.
§ 2. Таралатын толқындар әдісі. (Даламбер әдісі) .
Шексіз түзу есебіне көшеміз. Яғни х
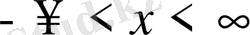 шейін өзгереді.
шейін өзгереді.
- Даламбер формуласы.
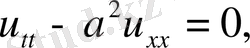
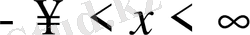 ,
,
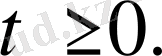 (1)
(1)
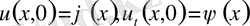 (2)
(2)
есепті қарастырамыз. (1) теңдеудің характеристикалық теңдеуі
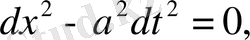
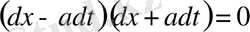
 немесе
немесе


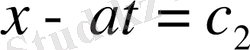
характеристикалары осылай анықталады. Енді
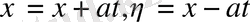 деген алмастырулар жасаймыз. Бұл алмастырулар нәтижесінде (1) теңдеу
деген алмастырулар жасаймыз. Бұл алмастырулар нәтижесінде (1) теңдеу
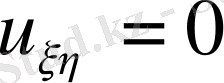 (3)
(3)
Ал бұл теңдеуді шешу оңай.
 бойынша интегралдаймыз.
бойынша интегралдаймыз.
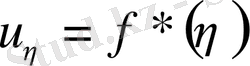
Тағы да интегралдасақ,
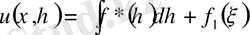
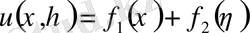 (4)
(4)
Енді
 -дан қайтадан
-дан қайтадан
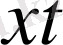 айысамыз.
айысамыз.
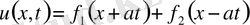 (5)
(5)
(5) (1) -дің шешімі. Онда ол (2) бастапқы шарттарды қанағаттанду керек.
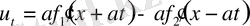
ал
 екенін ескерсек,
екенін ескерсек,
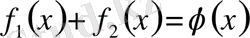
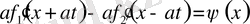
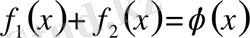
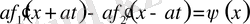
Қоссақ,
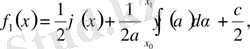
Алсақ,
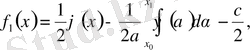
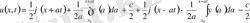
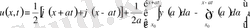
 (6)
(6)
(6) - Даламбер формуласы деп аталады.
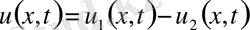 , мұндағы
, мұндағы
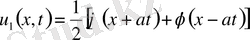 (7)
(7)
ал
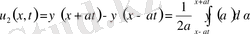 (8)
(8)
(1) -(2) есептің жалғыз шешімі (6) болады.
2. Біртекте емес теңдеулер.
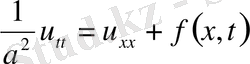 ,
,
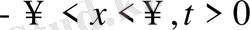 облысында қарастырамыз.
облысында қарастырамыз.
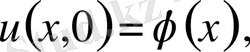
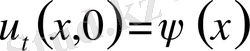 (9)
(9)
Есепті шығару үшін Даламбер формуласын қолданамыз. Ол үшін есепті келесі түрге келтіреміз.
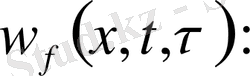
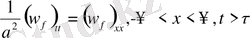 (10)
(10)
(10) теңдеудің шешімдерін қанағаттандыратын шарттар:
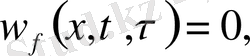
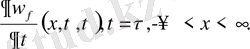 (11)
(11)
(10), (11) бұл есеп үшін Даламбер формуласы қолданылады. Онда
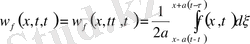 (12)
(12)
(12) формуланы пайдалана отырып, есептің шешімін мына түрде жазуға болатындығына көз жеткізейік. (9) шешімін мына түрде жазамыз.
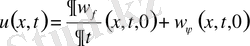 (13)
(13)
Мұндағы
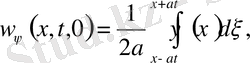
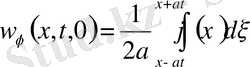
Лемма: Біртекті емес (9) теңдеудің шешімі, яғни (9) есептің шешімі бастапқы шарттарын ноль деп алғанда, яғни
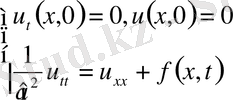 (*)
(*)
деп алғанда оның шешімі
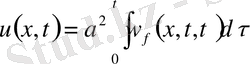 (14)
(14)
(14) шешімі екенін дәлелдеу үшін оны дифференциалдаймыз.
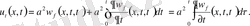
Екінші рет дифференциалдаймыз. Сонда
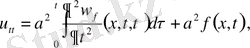
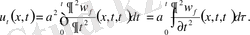
Сонымен (9) есептің шешімін жекелеген жеңіл есептердің шешімдерінің қосындысы түрінде құрамыз.
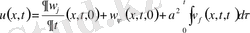 (15)
(15)
(12) формуланы пайдаланып, (15) формуладағы қосылғыштарды ашып жазамыз. Онда
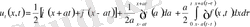 (16)
(16)
Сонымен (16) формула (9) есептің толық шешімін береді.
- Шешімнің орнықтылығы.
Шешімнің орнықтылығын зерттеу қажетті, орнықсыз шешімдер мағынасыз, қарастырылған есептердің шешімдері орнықты болу үшін бұл шешімдер қосымша шарттардан үзіліссіз тәуелді болу керек. Қандай
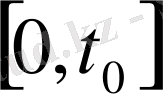 аралығында
аралығында
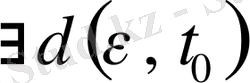 табылып,
табылып,
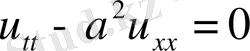 теңдеуінің екі шешімі үшін
теңдеуінің екі шешімі үшін
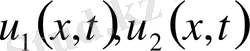 .
.
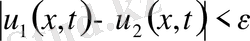 ,
,
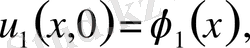
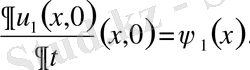
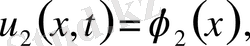
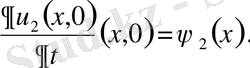
шарттары үшін тек қана
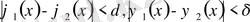
болғанда ғана орындалатын болса, шешім орнықты дейміз. Шешімнің бар және жалғыз болуы, орнықтығы мәселелерімен есептер қисынды, қисынсыз қойылған деп екі топқа бөлінеді. Есеп қисынды қойылған деп аталады, егер
- Шешімі бар болса,
- Қосымша шарттарды орындайтын жалғыз шешім болса.
- Шешім орнықты болса.
Егер бұл шарттардің әйтеуір біреуі орындалмаса есеп қисынсыз қойылған деп аталады. Практикада қисынсыз қойылған есептер де жиі кездеседі. Қисынсыз қойылған есептің мысалы:
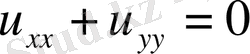 Лаплас теңдеуі
Лаплас теңдеуі
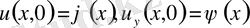 қарастырамыз. Бұл қисынсыз қойылған есеп екенін тексереміз.
қарастырамыз. Бұл қисынсыз қойылған есеп екенін тексереміз.
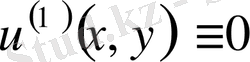 ,
,
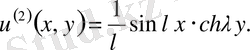
бастапқы шарттар мынадай
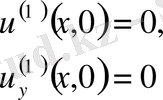
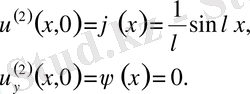
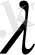 параметрі шексіз үлкен болған кезде
параметрі шексіз үлкен болған кезде
 бастапқы шарттары мен айырмалары аз. Шешім орнықсыз, демек қисынсыз есеп.
бастапқы шарттары мен айырмалары аз. Шешім орнықсыз, демек қисынсыз есеп.
- Жарты түзу және жалғастыру әдісі.
Енді жарты түзу есептерін қарастырайық, яғни түзудің бір шеті шектеулі болған жағдайды қараймыз.
 ,
,
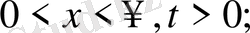
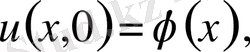
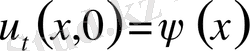 бастапқы шарттар.
бастапқы шарттар.
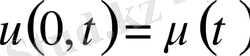 шекаралық шарттар.
шекаралық шарттар.
Бұл есепті жарты түзудің
бірінші шеттік есебі
деп атаймыз. Егер шекаралық шартта мынадай шарт қойылса
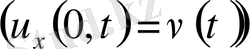 онда
екінші шеттік есебі
деп аталады.
онда
екінші шеттік есебі
деп аталады.
Бұл есептерді шешу үшін шексіз түзуде берілген есептердің шешімдерінің қасиеттерін пайдаланамыз.
Лемма
1:
Шексіз түзу есебіндегі бастапқы шарттар қандай да бір
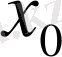 нүктесі арқылы тақ функциялар болса, онда шешім бұл нүктеде нольге айналады.
нүктесі арқылы тақ функциялар болса, онда шешім бұл нүктеде нольге айналады.
Лемма
2:
Шексіз түзу есебіндегі бастапқы шарттар қандай да бір
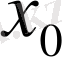 нүктесі арқылы жұп функциялар болса, онда шешімнің
нүктесі арқылы жұп функциялар болса, онда шешімнің
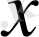 бойынша туындысы
бойынша туындысы
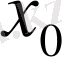 нүктесінде нольге айналады.
нүктесінде нольге айналады.
Л 1 Дәлелдеуі:
 деп аламыз.
деп аламыз.
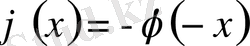 ,
,
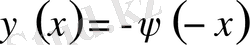 тақ болсын. Есептің шешімі
тақ болсын. Есептің шешімі
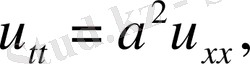
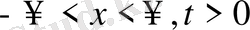
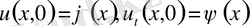
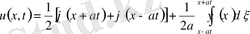
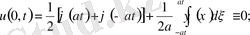
Лемма дәлелденді.
Леммалардың көмегімен келесі есептердің шешеміз
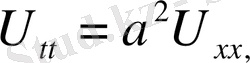
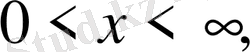
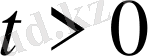 1-ші шектік есеп
1-ші шектік есеп
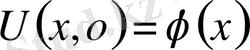
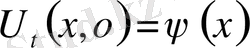
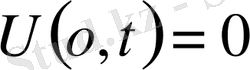
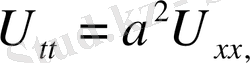
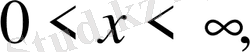
 2-ші шектік есеп
2-ші шектік есеп
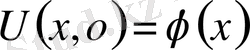
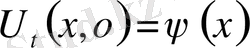

1-ші шектік есеп
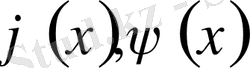
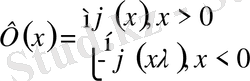
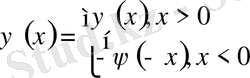
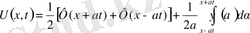


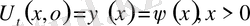
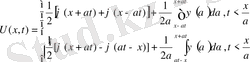
2-ші шектік есеп
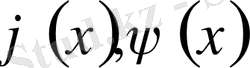
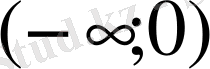
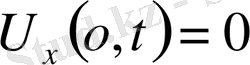
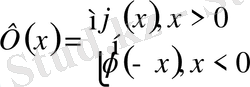
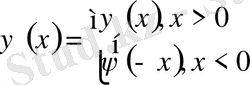
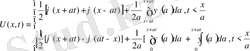
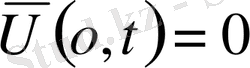 ,
,

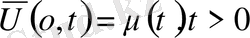
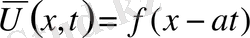
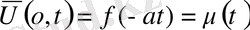
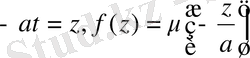
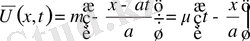
 облысында. Есептің шешімін барлық облыстар үшін табу керек.
облысында. Есептің шешімін барлық облыстар үшін табу керек.
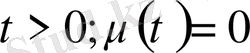
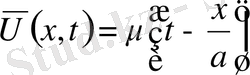
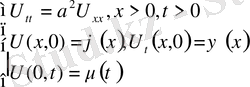
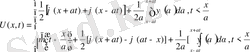
5. Кесінді есептері.
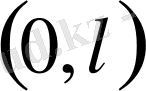 аралығында шектік есептер карастырамыз
аралығында шектік есептер карастырамыз
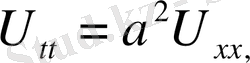
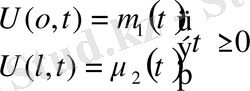
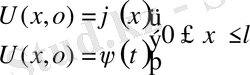
Бұл есепті шешу үшінде жалғастыру әдісі қарастырылады
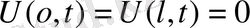
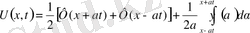
 функциялары
функциялары
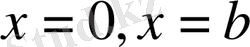 нүктелері арқылы тақ жалғастырылатын функциялар
нүктелері арқылы тақ жалғастырылатын функциялар
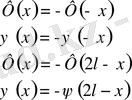
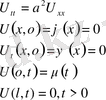
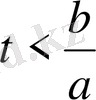
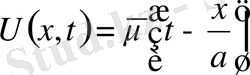
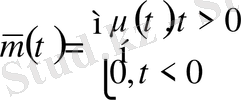
Бұл шешімнің қосындысы қатар түрінде жазылады. Усуптің шешімін береді.
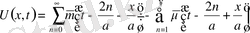
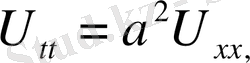
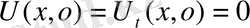
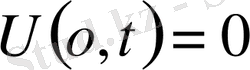
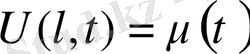
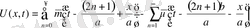
3 Айнымалыларды ажырату әдісі немесе Фурье әдісі.
1. Ішектің еркін тербеліс теңдеуі
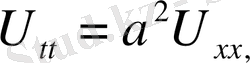 (1)
(1)
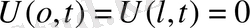 (2)
(2)
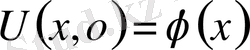
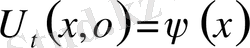 (3) қанағаттандыратын шешімді іздестіреміз.
(3) қанағаттандыратын шешімді іздестіреміз.
1-ші шектік есеп
Көмекші есепті қарастырамыз.
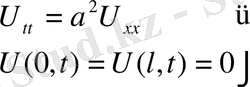
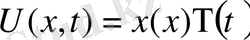 (4) осы түрде іздестіреміз
(4) осы түрде іздестіреміз
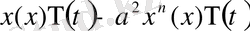 (5)
(5)
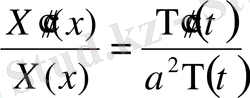 (6)
(6)
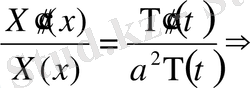 (7)
(7)
(7) әрқайсысын
 -ға теңестіреміз.
-ға теңестіреміз.
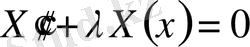 ,
,
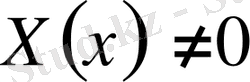 (8)
(8)
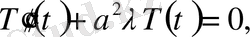
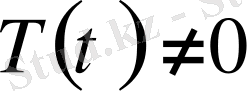 (9)
(9)
шекаралық шарттары
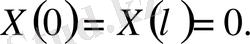
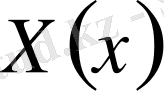 функциясын табу есебіне келдік. Бұл есепті
меншікті мәндер туралы есеп
деп аталады.
функциясын табу есебіне келдік. Бұл есепті
меншікті мәндер туралы есеп
деп аталады.
 - мәндерін табу керек. (8) теңдеудің ноль емес шешімдерін беретіндей
- мәндерін табу керек. (8) теңдеудің ноль емес шешімдерін беретіндей
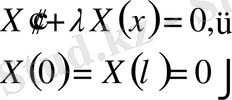 Штурм - Лиувилль есебі
деп аталады.
Штурм - Лиувилль есебі
деп аталады.
 - меншікті мәндеріне тиісті
- меншікті мәндеріне тиісті
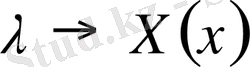 шешімдері есептің
меншікті функциялар
делінеді, характеристикалық теңдеуі
шешімдері есептің
меншікті функциялар
делінеді, характеристикалық теңдеуі
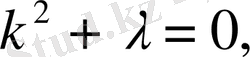 ал түбірлері
ал түбірлері
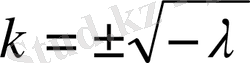
1.
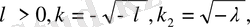 жалпы шешім
жалпы шешім
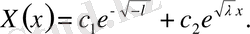 Енді шеттік шарттарды пайдаланамыз.
Енді шеттік шарттарды пайдаланамыз.
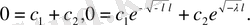
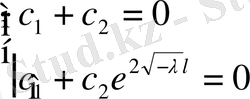
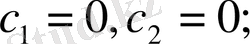 Мұнда тек нольдік шешім бар. Бұның қажеті жоқ, себебі ол қанағаттандырмайды.
Мұнда тек нольдік шешім бар. Бұның қажеті жоқ, себебі ол қанағаттандырмайды.
2.
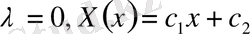 шеттік шарттарды пайдаланамыз.
шеттік шарттарды пайдаланамыз.
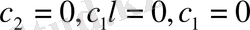 . Демек екі жағдайда да тек қана нольдік шешім бар.
. Демек екі жағдайда да тек қана нольдік шешім бар.
3.
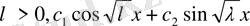 шеттік шарттарын қоямыз.
шеттік шарттарын қоямыз.
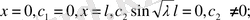
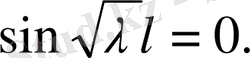
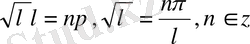
 -ның бұл мәндері
-ның бұл мәндері
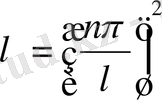 есептің ноль емес шешімдерін беретін меншікті мәндері.
есептің ноль емес шешімдерін беретін меншікті мәндері.
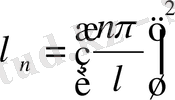 , яғни меншікті мәндері шексіз көп және меншікті функциялары шексіз көп.
, яғни меншікті мәндері шексіз көп және меншікті функциялары шексіз көп.
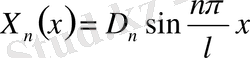 (10)
(10)
дербес шешімдерін береді.
 -ның бұл мәндерінде (2) теңдеудің шешімдері жазылады. Ол былай
-ның бұл мәндерінде (2) теңдеудің шешімдері жазылады. Ол былай
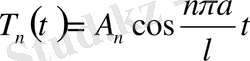 (11)
(11)
(10), (11) шешімдерінен
 шешімдері құрылады.
шешімдері құрылады.
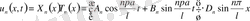
дифференциалдық теңдеу біртекті болғандықтан дербес шешімдерінің қосындысы да шешімді береді. Жалпы кез келген қатар түріндегі қосындысы да шешімді береді. Сонымен,
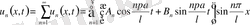 (13)
(13)
Бастапқы шарттарын орындалуын талап ете отырып
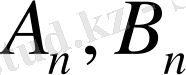 коэффициенттері анықталады.
коэффициенттері анықталады.
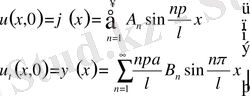 (14)
(14)
(14) өрнекті
 функцияларының Фурье қатарларына жіктелуі, тек
функцияларының Фурье қатарларына жіктелуі, тек
 бойынша жіктелуі. Демек, коэффициенттері былай анықталады.
бойынша жіктелуі. Демек, коэффициенттері былай анықталады.
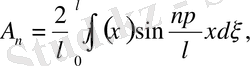 (15)
(15)
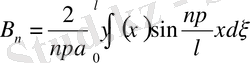 (16)
(16)
Қатарлар жинақы болғанда шешім толық анықталады. Бұл қатарлардың және туынды қатарлардың жинақылығы тікелей зерттеледі.
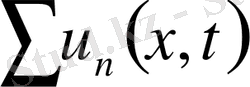
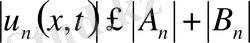
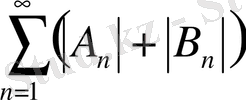 жинақы қатар екеніне көз жеткізе аламыз.
жинақы қатар екеніне көз жеткізе аламыз.
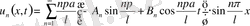
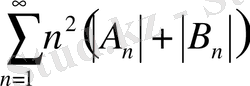
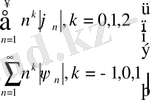
жалпы түрде мынадай қатар
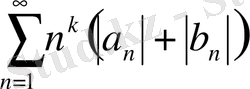
Бұл қатарлар
 функциясы екі рет дифференциалданатын болса,
функциясы екі рет дифференциалданатын болса,
 функциясы бір рет дифференциалданатын болса, жинақы қатарларды береді.
функциясы бір рет дифференциалданатын болса, жинақы қатарларды береді.
- Біртекті емес теңдеулер.
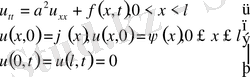 (17)
(17)
теңдеуді қарастырамыз. Теңдеу біртекті емес. Есептің шешімін
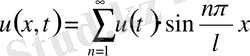 (18)
(18)
түрде іздестіреміз.
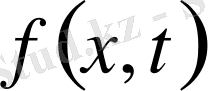 функциясы қатарға жіктеледі деп есептейміз.
функциясы қатарға жіктеледі деп есептейміз.

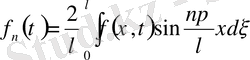 (19)
(19)
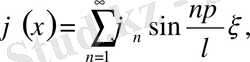
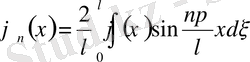 (20)
(20)
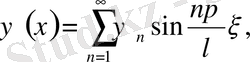
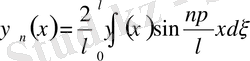 (21)
(21)
(18) шешімді (17) -ге қойсақ, мынадай теңдеу аламыз:
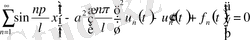
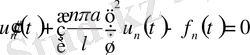 (22)
(22)
тұрақты коэффициентті кәдімгі дифференциалдық теңдеу (22) қосымша шартымен берілгенде Коши әдісімен шешіледі.
Бастапқы шарттардан мынаны аламыз.
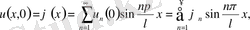 (23)
(23)
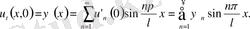 (24)
(24)
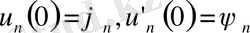
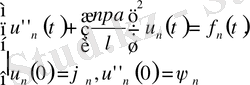 (25)
(25)
Сонымен бастапқы шарттармен қойылған кәдімгі дифференциалдық теңдеудің шешімін табу керек. Яғни (25) есепті шешеміз. (25) есептің шешімі, ол екі бөліктен тұрады.
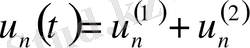 (26)
(26)
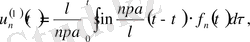 (27)
(27)
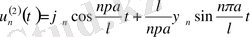 (28)
(28)
(28) біртекті теңдеудің шешімі, ал (27) біртекті емес теңдеудің әйтеуір бір шешімі. Онда ізделінді шешім
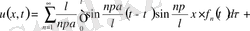
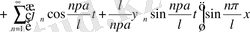 (29)
(29)
түрде жазылады. Яғни
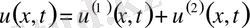 .
.
 -дәі мәніне қоямыз, сонда
-дәі мәніне қоямыз, сонда
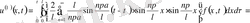
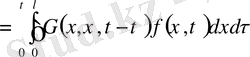 (30)
(30)
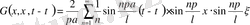 (31)
(31)
3. Жалпы бірінші шеттік есеп.
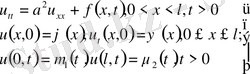 (32)
(32)
Есептің шешімі
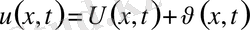 (33)
(33)
Түрде іздестіреміз. Мұндағы
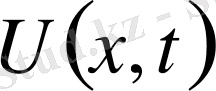 - белгілі деп қарастырылады.
- белгілі деп қарастырылады.
 функциясы келесі есептің шешімі түрінде іздестіріледі.
функциясы келесі есептің шешімі түрінде іздестіріледі.
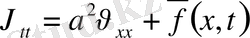 , мұндағы
, мұндағы
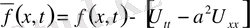
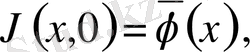 мұдағы
мұдағы
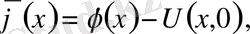
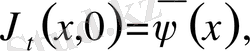 мұндағы
мұндағы
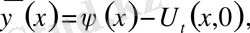
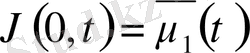 мұндағы
мұндағы
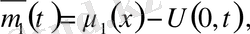
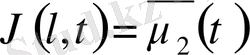 мұндағы
мұндағы
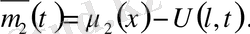
Қосымша есепті жеңілдетеміз, егер шеттік шарттарын ноль деп алсақ, яғни шеттік шарттары ноль болатын біртекті емес теңдеулерге келеміз. Сонымен,
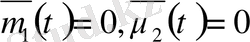 нольге айналатындай етіп таңдаймыз. Демек,
нольге айналатындай етіп таңдаймыз. Демек,
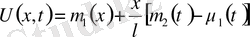 (34)
(34)
таңдау жеткілікті.
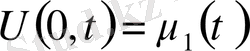
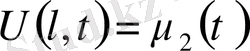
Сонымен біз қосымша есептің шешімін шеттік шарттары ноль болатын біртекті емес теңдеу шешіміне келтірдік, онда
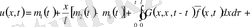
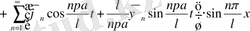 (35)
(35)
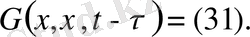
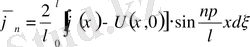
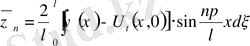
- Стационар біртекті емес шеттік есептер.
Стационар біртекті емес шеттік есептер тобы түрлі процестерде кездеседі. Бұл есептер тобына біртекті емес шартын орындайтын оң жақтағы функция
 уақыттан тәуелсіз және шеттік шарттарында уақыттан тәуелсіз делінеді.
уақыттан тәуелсіз және шеттік шарттарында уақыттан тәуелсіз делінеді.
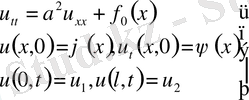 (36)
(36)
біртекті емес стационар бірінші шеттік есепті қарастырамыз. Бұл есептің шешімін де мына түрде іздестіреміз.
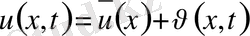 мұндағы
мұндағы
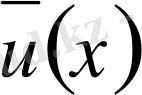 белгілі функция
белгілі функция
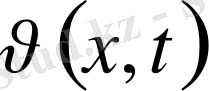 -келесі есептен анықтаймыз.
-келесі есептен анықтаймыз.
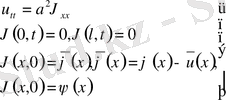
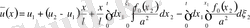
Егер
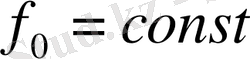 болса, онда
болса, онда
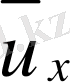 былай анықталады.
былай анықталады.
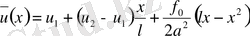
(36) есептің шешімі мына түрде жазылады.
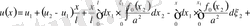
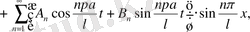 (37)
(37)
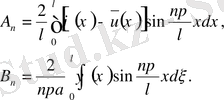
- Бастапқы шартсыз есептер.
Шекарада қойылған шарттың таралуын көрсететін есептер тобы бар. Бұл есептер тобында бастапқы шарттар ескерілмейді, яғни процесс басталуынан әлде қайда ұзақ уақытта деп алынады.
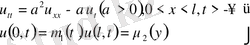 (38) бастапқы шартсыз есеп.
(38) бастапқы шартсыз есеп.
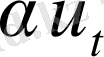 кедергі күшіне пропорционал. Практикада шеттік шарттары перодты функциялармен өрнектелетін жағдайлар жиі кездеседі.
кедергі күшіне пропорционал. Практикада шеттік шарттары перодты функциялармен өрнектелетін жағдайлар жиі кездеседі.
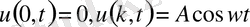 немесе
немесе
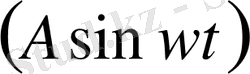
(38) есепті нақты былай етіп жазсақ болады.
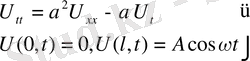 (39)
(39)
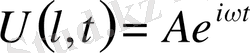
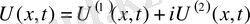
Нақты бөлігіде жорамал бөлігіде шешімді береді.

 шаттарды анықталады.
шаттарды анықталады.
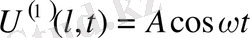
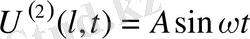
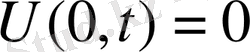
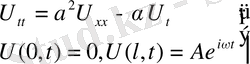 (40)
(40)
Есептін шешімін мына турде іздестіреміз
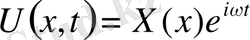

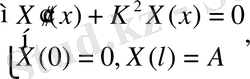
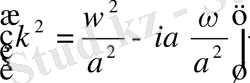 (41) (42)
(41) (42)
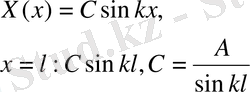 (43)
(43)
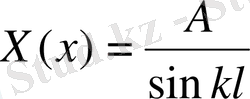
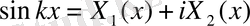 (44)
(44)
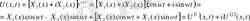
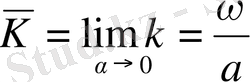 ,
,
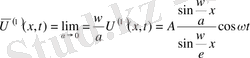
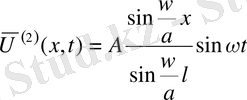
6. Шоғырланған күш
 нүктесінде әсер етуші күш бар деп есептейміз. Егер күшіміз
нүктесінде әсер етуші күш бар деп есептейміз. Егер күшіміз
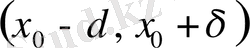 аралығында әсер ететін болса, онда
аралығында әсер ететін болса, онда
 отырып күштердің әсерін
отырып күштердің әсерін
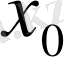 нүктесінде шоғырландыруға болады.
нүктесінде шоғырландыруға болады.
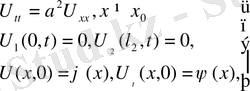
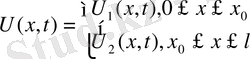
Мұндай жағдайда қосымша шарт қажет. Мұндай шарт түйіндес шарт деп аталады.
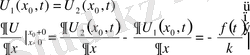
(48) -түйіндес шарт.
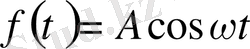 ,
,
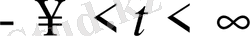 әсер етіп отырған функция периодты болсын. Осы есепті қарастырайық. 47 есепті 48-ші шартымен қарастырады.
әсер етіп отырған функция периодты болсын. Осы есепті қарастырайық. 47 есепті 48-ші шартымен қарастырады.
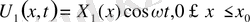
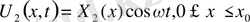
Бұл шешімдерді 47-ге қоямыз.
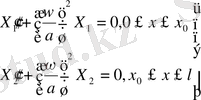 ( 49)
( 49)
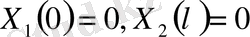 (50)
(50)
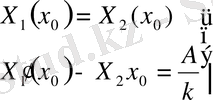 (51)
(51)
49-шы теңдеуді 50, 51 шарттарымен шешсек мыналарды аламыз.
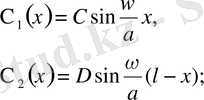
51 шартты пайдалансақ C мен D тұрақтыларын аламыз.
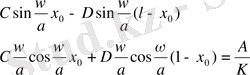
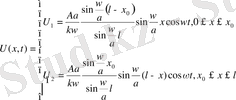
Дәл осылацша
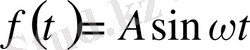 болғандағы шешімдіде жазамыз.
болғандағы шешімдіде жазамыз.
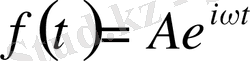 функциясы болса, онда шешімін мына түрде жазамыз.
функциясы болса, онда шешімін мына түрде жазамыз.

Математикалық анализдегі қағиданы пайдаланып . . . емес функциялар үшін де шешімдер құруға болады. Мұнда белгілі бір аралықта функцияны периодты деп жалғастырып функцияның өзін жалғастарамыз. Яғни Фурье қатарларына жіктеп барып жоғарыдағыдай формула аламыз.
7. Айнымалыларды ажыратудың жалпы схемасы.
Теріс теңдеудегі
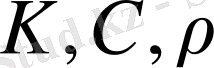 коэфиценттері тұрақты емес болған жағдайда айнымалыларды ажырату әдісін қолдануға болады. Жалпы түрдегі теңдеу қарастырамыз.
коэфиценттері тұрақты емес болған жағдайда айнымалыларды ажырату әдісін қолдануға болады. Жалпы түрдегі теңдеу қарастырамыз.
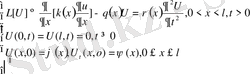 (53)
(53)
53 есептің шешімінде айнымалыларды ажырату әдісмен табуға болады. Ол үшін тағы мынаны пайдаланамыз.
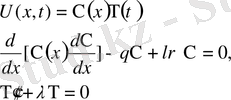
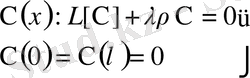 (54)
(54)
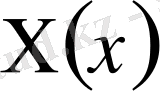 үшін Штурм-Лиувилль меншікті мәндер және меншікті функциялар есебіне келеміз. Яғни
үшін Штурм-Лиувилль меншікті мәндер және меншікті функциялар есебіне келеміз. Яғни
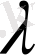 меншікті мәндер табу керек және әрбір
меншікті мәндер табу керек және әрбір
 -ға тиісті меншікті функцияларды табу керек . 54 -ші есептің шешімдерін құратындай кейде бұл меншікті мәндерді, меншікті функцияларды
-ға тиісті меншікті функцияларды табу керек . 54 -ші есептің шешімдерін құратындай кейде бұл меншікті мәндерді, меншікті функцияларды
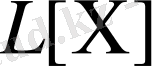 операторының меншікті мәндері, меншікті функциялары деп аталады.
операторының меншікті мәндері, меншікті функциялары деп аталады.
Негізгі қасиеттер
1 меншікті мәндердің жиыны
 саналымды. Бұл мәндерге тиісті меншікті функцияларда
саналымды. Бұл мәндерге тиісті меншікті функцияларда
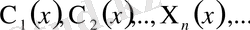 саналымды.
саналымды.
2
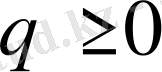 болғанда
болғанда
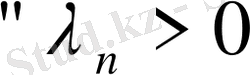
3
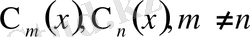
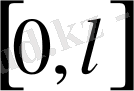 аралығында
аралығында
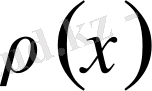 салмағымен ортогональ. Яғни
салмағымен ортогональ. Яғни
 (55)
(55)
4
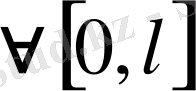 аралындағы екі рет үздіксіз дифференциалдық функция
аралындағы екі рет үздіксіз дифференциалдық функция
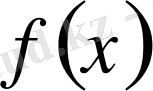
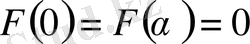 шарттарын қанағаттандырса, онда
шарттарын қанағаттандырса, онда
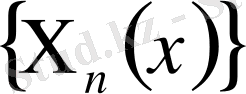 меншікті функция арқылы біркелкі және абсолютті жинақы қатарға жіктеледі.
меншікті функция арқылы біркелкі және абсолютті жинақы қатарға жіктеледі.
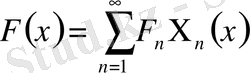 (56)
(56)
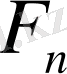 коэффиценттері былай анықталады.
коэффиценттері былай анықталады.
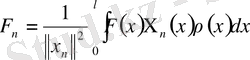 (57)
(57)
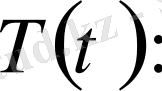
 (59)
(59)
Бұл оңай шешіледі. Характеристикалық теңдеу комплекс айнымалы функция болады. Шешімі
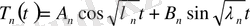 - жалпы шешім.
- жалпы шешім.

Суперпозиция принципі бойынша кез келген қосынды шешімді береді.
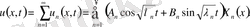
бастапқы шарттарды пайдаланамыз.
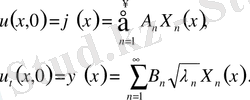


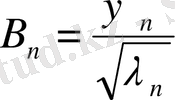 (60)
(60)
§ 4. Характеристикаларында шарттар қойылған есептер.
- Есептің қойылуы.
Қосымша шарттар
 немес
немес
 сызықтарында, ал жалпы жағдайда
сызықтарында, ал жалпы жағдайда
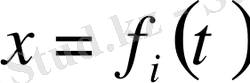 сызықтарында қойылатын есептерде практикада жиі кездеседі. Осындай есептің бірі
Гурса есебі
деп аталады.
сызықтарында қойылатын есептерде практикада жиі кездеседі. Осындай есептің бірі
Гурса есебі
деп аталады.
- Гурса есебі үшін тізбекпен жуықтау әдісі.
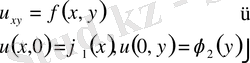 (1)
(1)
Гурса есебін қарастырамыз.
 ,
,
 түзулері (1) есептің характеристикалары.
түзулері (1) есептің характеристикалары.
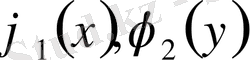 функциялары дифференциалданатын дей отырып есептің шешімін іздестіреміз. Бұл функцияларға түйіндестік шартын қосамыз, яғни
функциялары дифференциалданатын дей отырып есептің шешімін іздестіреміз. Бұл функцияларға түйіндестік шартын қосамыз, яғни
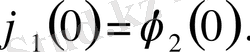
(1) -дің екі жағын интегралдаймыз.
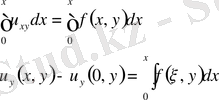
немесе
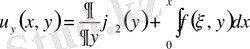 у бойынша интегралдаймыз.
у бойынша интегралдаймыз.
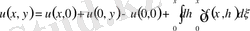
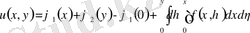 (2)
(2)
Бұл шешім жалпы жалғыз шешім болатындығы айқын. Енді күрделірек есепті қарастырайық.
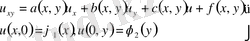 (3)
(3)
Мұнда
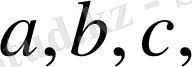
 функциялары үзіліссіз функциялар деп аталады.
функциялары үзіліссіз функциялар деп аталады.
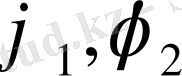 алдыңғы есептегі шарттарды орындайды.
алдыңғы есептегі шарттарды орындайды.
Есептің шешімі интегро - дифференциалдық теңдеуге келтіріледі.
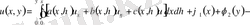
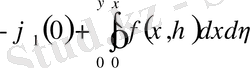 (4)
(4)
ізделінді функция интеграл сыртында да, астында да дифференциал астында да берілгендіктен бұл теңдеуді интегро - дифференциалдық теңдеу деп аталады. Интегро - дифференциалдық теңдеуді, яғни (4) шешу үшін тізбекпен жуықтау әдісін пайдаланамыз. Ол үшін
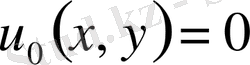
онда
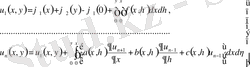 (5)
(5)
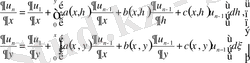 (6)
(6)
Мына
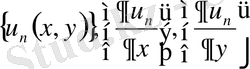 тізбектердің біркелкі жинақталатынын көрсетуге болады. Ол үшін мынадай айырым қарастырылады.
тізбектердің біркелкі жинақталатынын көрсетуге болады. Ол үшін мынадай айырым қарастырылады.
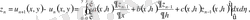
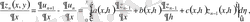
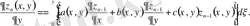
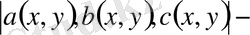 шектеулі болу керек.
шектеулі болу керек.
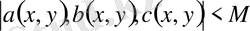 берілген облыста шектеулі.
берілген облыста шектеулі.
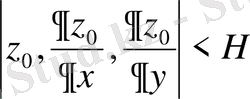
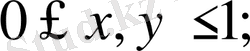
Онда мынадай бағалулар орындалады.
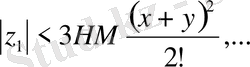
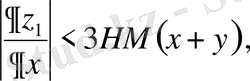

Онда
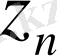 үшін мына бағалау орынды.
үшін мына бағалау орынды.
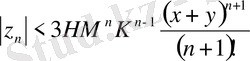
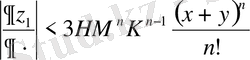
Бұл бағалау
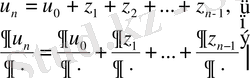
Тізбектерінің біркелкі жинақы екендігін көрсетеді. Яғни,
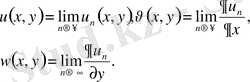
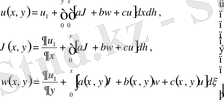 (7)
(7)
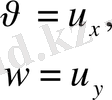
 интегро - дифференциалдық теңдеуді қанағаттандыратынын көрсетеді. Енді шешімнің жалғыз екендігіне көз жеткіземіз. Ол үшін кері жориық, яғни екі шешімі бар делік.
интегро - дифференциалдық теңдеуді қанағаттандыратынын көрсетеді. Енді шешімнің жалғыз екендігіне көз жеткіземіз. Ол үшін кері жориық, яғни екі шешімі бар делік.
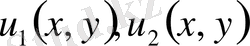
Екі шешімнің айырымын қарастырайық.
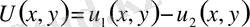
онда
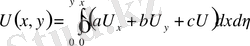
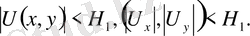
онда
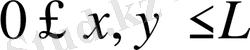 аралықта мына теңсіздік орындалады.
аралықта мына теңсіздік орындалады.
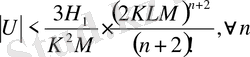 үшін орындалады.
үшін орындалады.
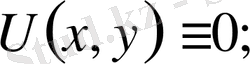
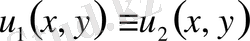 .
.
§5. Гипербола тектес жалпы сызықтық теңдеуді шешу.
- Түйіндес дифференциалдық операторлар.
 (1)
(1)
операторын енгіземіз. Бұл сызықтық дифференциалдық оператор. Бұл операторды
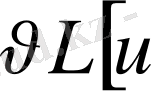 көбейтіп, мүшелеп жазайық.
көбейтіп, мүшелеп жазайық.
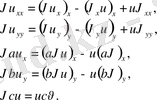
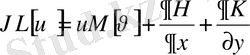 (2)
(2)
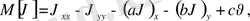 (3)
(3)
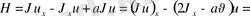 (4)
(4)
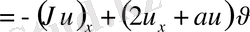 (4´)
(4´)
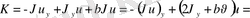 (5)
(5)
 (5´)
(5´)
Дифференциалдық операторлар немесе екі дифференциалдық оператор
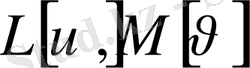 түйіндес оператор
деп аталады, егер
түйіндес оператор
деп аталады, егер
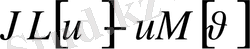
айырымы қандайда бір
 өрнектерінің дербес туындыларының, яғни х және у бойынша комбинациясына тең болсын. Қарастырылып отырған
өрнектерінің дербес туындыларының, яғни х және у бойынша комбинациясына тең болсын. Қарастырылып отырған
 операторлары түйіндес. Егер бұл операторлар үшін
операторлары түйіндес. Егер бұл операторлар үшін
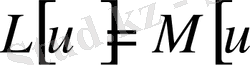
орындалса, онда операторды Өзіне-өзі түйіндес деп аталады. Қандай да бір жазықтық облыс қарастырсақ, онда осы облыс бойынша алынған екі еселік интеграл
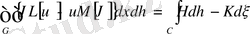 (6)
(6)
тең болады. Мұндағы
 екі рет дифференциалданатын функциялар. (6) формуланы
екі өлшемді Грин формуласы
деп те атайды.
екі рет дифференциалданатын функциялар. (6) формуланы
екі өлшемді Грин формуласы
деп те атайды.
- Шешімнің интегралдық түрі.
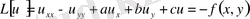 (7)
(7)
теңдеуінің
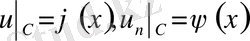 (7´)
(7´)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz