Екінші ретті сызықты жартылай туынды теңдеулер: типтері, канондық түрге келтіру және шешу әдістері (1-24 мысал)


1-мысал . Дербес туындылы
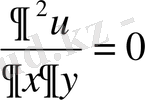 (1. 13)
(1. 13)
теңдеуінің жалпы шешімін табу керек .
Шешуі: Берілген теңдеуді
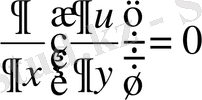
түрінде жазайық. Осыдан
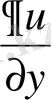 туындысының
туындысының
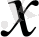 бойынша туындысы нөлге тең болғандықтан ол
бойынша туындысы нөлге тең болғандықтан ол
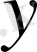 ке тәуелді функция екендігі шығады, яғни
ке тәуелді функция екендігі шығады, яғни
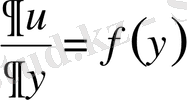 .
.
Сондықтан
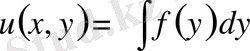 .
.
Мұндағы кез келген
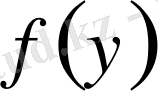 функциясының интегралы
функциясының интегралы
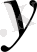 -ке тәуелді
-ке тәуелді
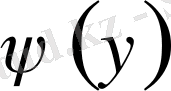 функциясы мен тұрақты деп саналатын кез келген
функциясы мен тұрақты деп саналатын кез келген
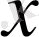 -ке тәуелді
-ке тәуелді
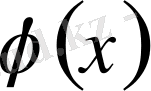 функциясының қосындысынан тұрады.
функциясының қосындысынан тұрады.
Сонымен берілген теңдеудің жалпы интегралы
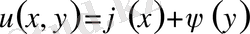 (1. 14)
(1. 14)
2-мысал. Екінші ретті
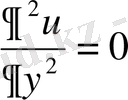 (1. 15)
(1. 15)
теңдеуінің жалпы шешімін табу керек.
Шешуі: Теңдеуді
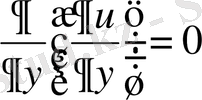
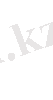
түрінде жазайық. Сонда
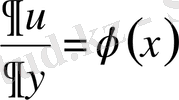 , яғни ол
, яғни ол
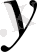 тен тәуелсіз функция екендігі көрінеді.
тен тәуелсіз функция екендігі көрінеді.
Интегралдаудан кейін
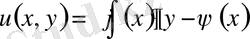 , яғни
, яғни
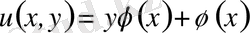 (1. 16)
(1. 16)
шешімін аламыз.
3-мысал . Берілген
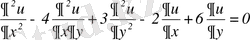
теңдеуін канондық түрге келтіру керек.
Шешуі:
Бұл теңдеуде
 ,
,
 ,
,
 болғандықтан
болғандықтан
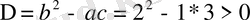 ,
,
яғни теңдеу гиперболалық типке жатады. Сипаттамалық теңдеуі мына түрде жазылады.
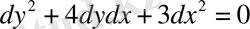 , немесе
, немесе
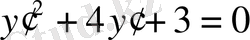
Оның түбірлері
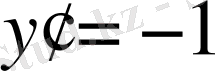 ,
,
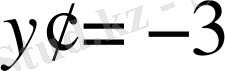 , болады да бірінші интегралдары (сипаттауыштары)
, болады да бірінші интегралдары (сипаттауыштары)
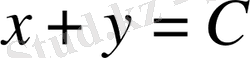 ,
,
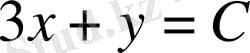
түрінде алынады.
Теңдеуді канондық түрге келтіру үшін жаңа айнымалылар енгіземіз
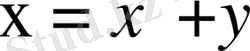 ,
,
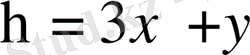
Теңдеуге қойып түрлендіру үшін осы айнымалылардың дербес туындыларын табайық.
Алдымен ескі айнымалылар бойынша туындыларды жаңа айнымалылар бойынша туындылармен өрнектеу формулаларын келтірейік.
Айталық,
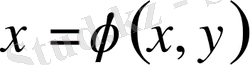 ,
,
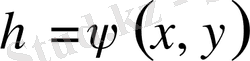 (1. 17) екі рет үздіксіз дифференциалданатын функциялар болсын. Сонда төмендегідей туынды формулалары алынады:
(1. 17) екі рет үздіксіз дифференциалданатын функциялар болсын. Сонда төмендегідей туынды формулалары алынады:
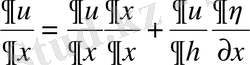 ;
;
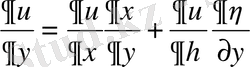 ;
;
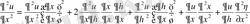 ;
;
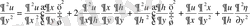
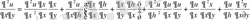 Ескерту:
Ескерту:
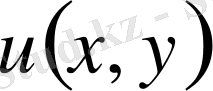 функциясын жаңа
функциясын жаңа
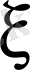 және
және
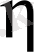 айнымалылармен өрнектеу формуласын қарастырайық
айнымалылармен өрнектеу формуласын қарастырайық
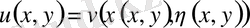 (1. 19)
(1. 19)
Әдетте (1. 18) формулаларда v-ның орнына u деп ауыстырып жазады. Бірақ та
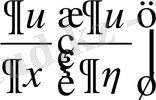 туындыларын η=const (ξ =const) сызықтары бойынша алынған
туындыларын η=const (ξ =const) сызықтары бойынша алынған
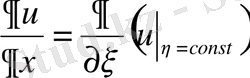 туындысы, ал дұрысында
туындысы, ал дұрысында
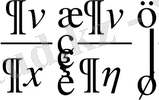 деп ұғу керек.
деп ұғу керек.
Өйткені «
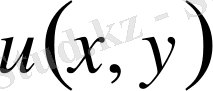 функциясының
функциясының
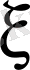 немесе
немесе
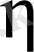 бойынша дербес туындысы» дегеннің екінші
бойынша дербес туындысы» дегеннің екінші
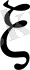 немесе
немесе
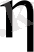 координаты алынғанша мағынасы жоқ. . Шынында да,
координаты алынғанша мағынасы жоқ. . Шынында да,
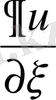 туындысы
туындысы
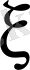 айнымалысын ғана емес туындыда ашық көрінбесе де
айнымалысын ғана емес туындыда ашық көрінбесе де
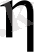 айнымалысын таңдап алудан тәуелді.
айнымалысын таңдап алудан тәуелді.
Енді мысалымыздағы
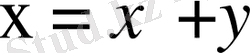 және
және
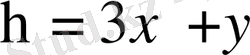 жаңа айнымалылары бойынша дербес туындыларды есептейік:
жаңа айнымалылары бойынша дербес туындыларды есептейік:
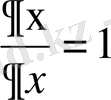 ,
,
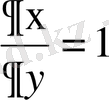 ,
,
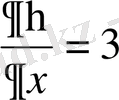 ,
,
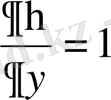
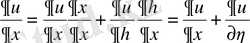 ;
;
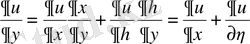 ;
;
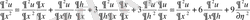 ;
;
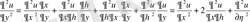 ;
;
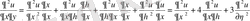
Осыларды берілген теңдеуге апарып қоямыз:

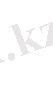 Осыдан
Осыдан
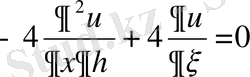 , немесе
, немесе
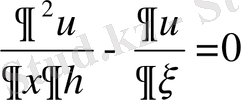 - берілген теңдеудің канондық түрін аламыз.
- берілген теңдеудің канондық түрін аламыз.
4-мысал . Берілген
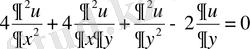
теңдеуін канондық түрге келтіру керек .
Шешуі:
Бұл жағдайда
 ,
,
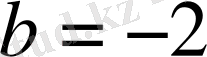 ,
,
 және
және
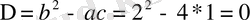 ,
,
болғандықтан теңдеу параболалық типке жатады.
Сипаттамалық теңдеу
4dy
2
-4dxdy+dx
2
=0, немесе
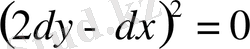
Осыдан
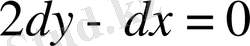 ,
,
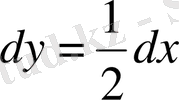 ,
,
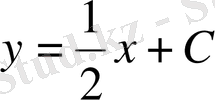 - бірінші интеграл.
- бірінші интеграл.
Сондықтан
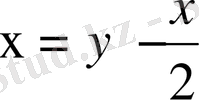 деп аламыз. Ал екінші сипаттауыш үшін кез келген
деп аламыз. Ал екінші сипаттауыш үшін кез келген
 функциясын алуға болады. Өйткені бұл функциялардың Якобианы нөлге тең болмайды:
функциясын алуға болады. Өйткені бұл функциялардың Якобианы нөлге тең болмайды:
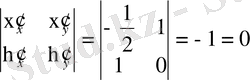
Сонымен жаңа айнымалыларды
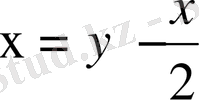 ,
,
 бойынша дербес
бойынша дербес
туындыларды есептейміз:
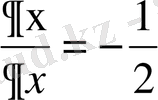 ,
,
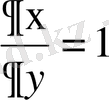 ,
,
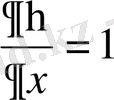 ,
,
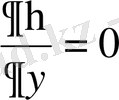
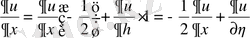 ;
;
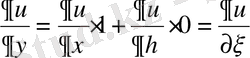 ;
;
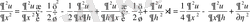
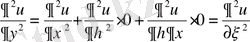 ;
;
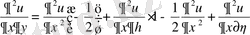 .
.
Теңдеуге апарып қойып оның канондық түрін табамыз:
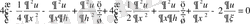 ,
,
немесе
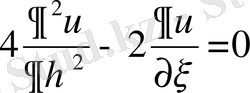 .
.
Сонымен
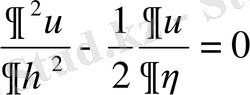 берілген теңдеудің канондық түрі.
берілген теңдеудің канондық түрі.
5-мысал.
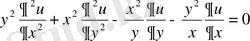
теңдеуінің типін анықтап канондық түрге келтіру керек.
Шешуі:
 және
және
 түзулерінде жатпайтын нүктелерде
түзулерінде жатпайтын нүктелерде
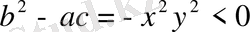 болғандықтан берілген теңдеу эллипстік типке жатады. Оның сипаттамалық теңдеуін құрайық
болғандықтан берілген теңдеу эллипстік типке жатады. Оның сипаттамалық теңдеуін құрайық
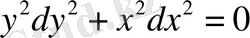 .
.
Мұны екі теңдеу түрінде жазуға болады
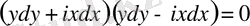
Осыдан
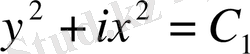 және
және
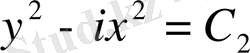
екі бірінші интегралдарын аламыз.
Сондықтан
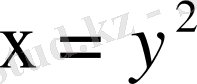 және
және
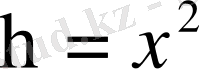 деп алып дербес туындыларды есептейміз.
деп алып дербес туындыларды есептейміз.
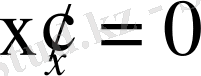 ,
,
 ,
,
 ,
,
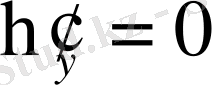 ,
,
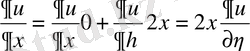 ;
;
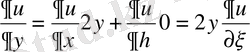 ;
;
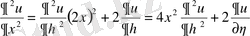 ;
;
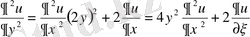
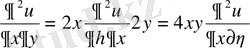 .
.
Осы мәндерді берілген теңдеуге қойып оның канондық түріне келеміз
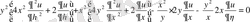 ,
,
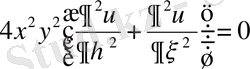 немесе
немесе
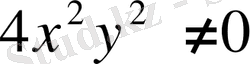 -ге қысқартып
-ге қысқартып
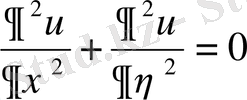
теңдеуін аламыз.
6-мысал . Берілген
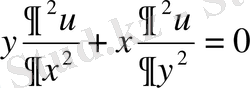
теңдеуін канондық түрге келтіру керек.
Шешуі: Сипаттамалық теңдеу-
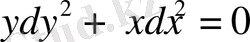
түрінде жазылады. Оны
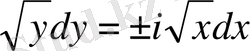 теңдеуі түрінде жазып, берілген теңдеу эллипстік типке жататындығын анықтаймыз.
теңдеуі түрінде жазып, берілген теңдеу эллипстік типке жататындығын анықтаймыз.
Бұл теңдеуді интеграалдау нәтижесінде
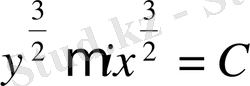 шешімін аламыз.
шешімін аламыз.
Егер жаңа координаталар үшін
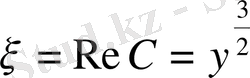 ,
,
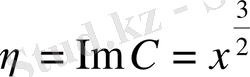
айнымалыларын алатын болсақ, онда дербес туындылар мынадай түрде алынады:
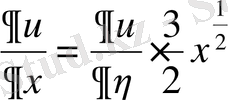 ;
;
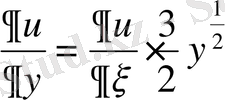 ;
;
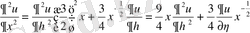 ;
;
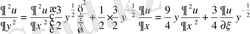 .
.
Осы мәндерді теңдеуге қойып, түрлендірулерден кейін теңдеудің канондық түріне келеміз:
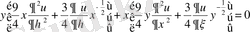 ,
,
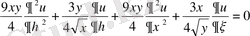
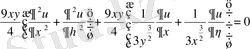 , немесе
, немесе
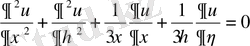
Осыдан
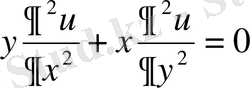 теңдеуі
теңдеуі
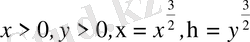
және
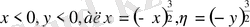 болғанда, яғни бірінші және үшінші ширектерде эллипстік типке жататындығы көрінеді.
болғанда, яғни бірінші және үшінші ширектерде эллипстік типке жататындығы көрінеді.
Егер
 , ал
, ал
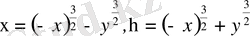 және
және
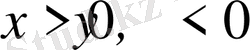 , ал
, ал
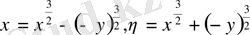
болғанда теңдеудің канондық түрі
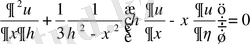
теңдеуімен өрнектеледі, яғни
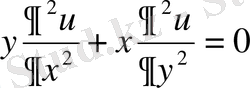
теңдеуі екінші және төртінші ширектерде гиперболалық типке жататындығы анықталады. Егер
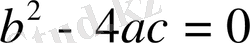 болса, координата осьтерінің нүктелерінде теңдеу параболалық типке жатады. Бұл жағдайда сипаттамалық теңдеудің бір ғана
болса, координата осьтерінің нүктелерінде теңдеу параболалық типке жатады. Бұл жағдайда сипаттамалық теңдеудің бір ғана
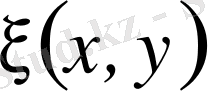 бірінші интегралы бар болады. Теңдеуді канондық түрге келтіру үшін екінші
бірінші интегралы бар болады. Теңдеуді канондық түрге келтіру үшін екінші
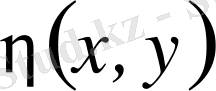 сипаттауышын түрлендіру анықтауышы (Якобианы) нөлге тең болмайтындай етіп кез келген функция түрінде алады.
сипаттауышын түрлендіру анықтауышы (Якобианы) нөлге тең болмайтындай етіп кез келген функция түрінде алады.
7-мысал . Берілген
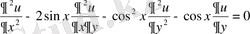
теңдеуінің жалпы шешімін табу керек.
Шешуі: Бұл теңдеу үшін
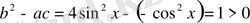 ,
,
яғни теңдеу гиперболалық типке жатады.
Сипаттамалық теңдеуін жазайық
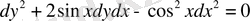 ,
,
немесе
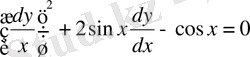
Осыдан
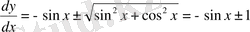 . Интегралдаудан
. Интегралдаудан
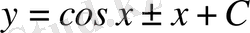 шешімі алынады.
шешімі алынады.
Олай болса
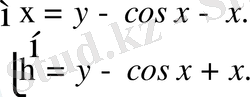
Енді берілген теңдеуде айнымалыларды ауыстырайық:
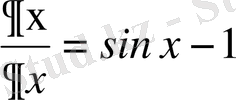 ,
,
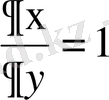 ,
,
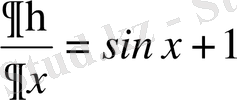 ,
,
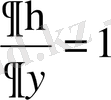 ;
;
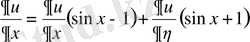 ,
,
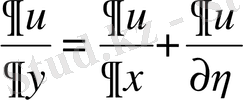

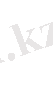
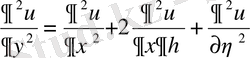 ,
,
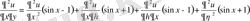 .
.
Осы туындылар мәндерін теңдеуге қоямыз:

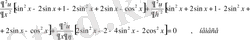
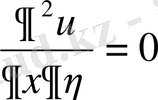 .
.
Бұл теңдеудің жалпы шешімі
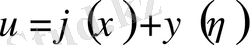 .
.
Алғашқы айнымалыларға көшіп берілген теңдеудің жалпы шешімін аламыз.

8-мысал . Егер
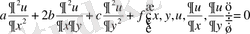
теңдеуі сызықты және коэффициенттері тұрақты болса, онда жаңа айнымалылар арқылы түрлендірулерден кейін әрбір жағдайда тағы да коэффициенттері тұрақты сызықтық теңдеулер алынады
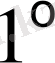
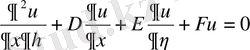

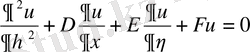

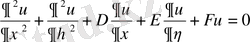
Бұл теңдеулерді жаңадан белгісіз v функциясын енгізіп әрі қарай тағы да ықшамдауға болады. Жаңа функцияның түрі:
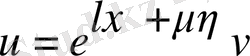 .
.
Мұндағы
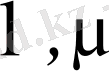 тұрақтыларын әдейілеп таңдап алуға болады. Сонда жоғарыдағы теңдеулерді мынадай түрлерге келтіруге болады.
тұрақтыларын әдейілеп таңдап алуға болады. Сонда жоғарыдағы теңдеулерді мынадай түрлерге келтіруге болады.
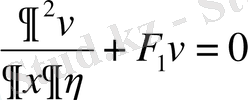

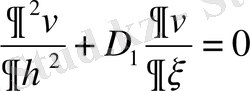

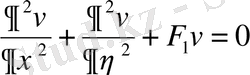
Мысалы, айнымалыны ауыстыру функциясын дифференциалдағаннан кейін
 функциясы мен оның туындыларын
функциясы мен оның туындыларын
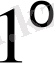 ге қойып және ұқсас мүшелерін жинастырғаннан кейін мынадай теңдеу аламыз:
ге қойып және ұқсас мүшелерін жинастырғаннан кейін мынадай теңдеу аламыз:
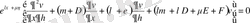
Әрі қарай
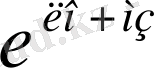 ға қысқартып,
ға қысқартып,
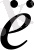 мен
мен
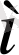 ды
ды

болатындай етіп алып
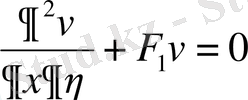
теңдеуін аламыз.
9-мысал . Берілген
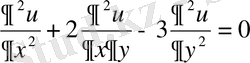
теңдеуінің
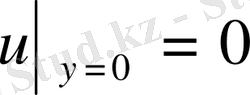 ,
,
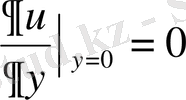
алғашқы шарттарын қанағаттандыратын шешімін табу керек.
Шешуі: Алдымен теңдеудің жалпы шешімін анықтайық. Ол үшін сипаттамалық теңдеуін құрайық:
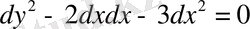 немесе
немесе
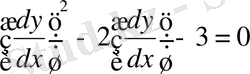
Осыдан
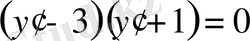 ,
,
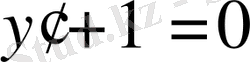 ,
,
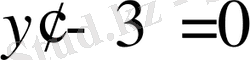
теңдеулеріне көшіп, олардың бірінші интегралдарын анықтаймыз:
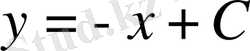 және
және
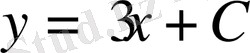
Олай болса
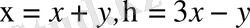 жаңа айнымалылары енгізіп дербес туындыларды есептейміз.
жаңа айнымалылары енгізіп дербес туындыларды есептейміз.
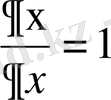 ,
,
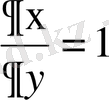 ,
,
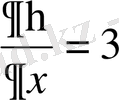 ,
,
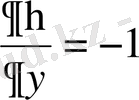 ,
,
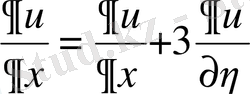 ,
,
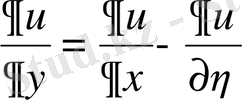 ,
,
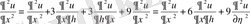 ,
,
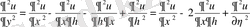 ,
,
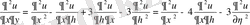 .
.
Осы мәндерді берілген теңдеуге қоямыз :
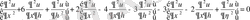
немесе,
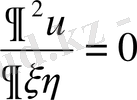 түріндегі канондық теңдеу алынады.
түріндегі канондық теңдеу алынады.
Оның жалпы шешімі
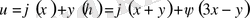
Енді алғашқы шарттарды пайдаланамыз
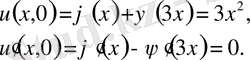
Бірінші теңдеуді дифференциалдап
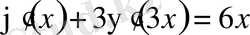 теңдеуін аламыз. Сонан соң
теңдеуін аламыз. Сонан соң
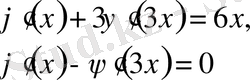
жүйесіннен
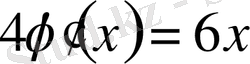 ,
,
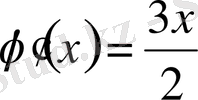 теңдіктерін аламыз. Осыны интегралдаудан кейін
теңдіктерін аламыз. Осыны интегралдаудан кейін
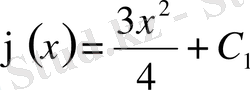
шешімін аламыз.
Олай болса,
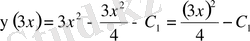 болады да
болады да
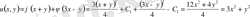 яғни,
яғни,
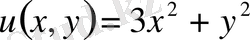 - берілген есептің шешімі.
- берілген есептің шешімі.
18-мысал.
Ұзындығы
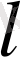 -ға тең шеттері бекітілген шектің алғашқы уақыттағы пішіні
-ға тең шеттері бекітілген шектің алғашқы уақыттағы пішіні
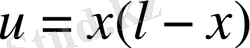 параболаға ұқсайды. Шекті бастапқы жылдамдықсыз босатып жібергендегі оның тербеліс заңын табу керек.
параболаға ұқсайды. Шекті бастапқы жылдамдықсыз босатып жібергендегі оның тербеліс заңын табу керек.
Шешуі:
Шектің нүктелерінің ауытқуы (2. 42) формула арқылы, ал оның коэффициенттері (2. 43) формулалар арқылы анықталады. Сол формулалар бойынша
 болады. Енді
болады. Енді
 коэффициентін есептейік:
коэффициентін есептейік:
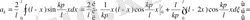
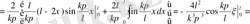
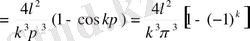
Осы мәндерді (2. 42) формулаға қойып есептің шешімін аламыз
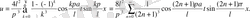
19-мысал.
Шектің шеттері
 және
және
 нүктелерінде қатаң бекітілген. Ауытқулардың алғашқы уақыт мезгіліндегі түрі
нүктелерінде қатаң бекітілген. Ауытқулардың алғашқы уақыт мезгіліндегі түрі
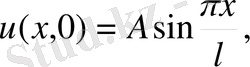
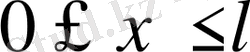 .
.
Бастапқы жылдамдықтар нөлге тең. Шектің ауытқуларын анықтау керек.
Шешуі: Бұл есепті бұрын басқа әдіспен шығарған болатынбыз. Енді Фурье әдісін қолданайық. Ол үшін шектің тербелістерінің теңдеуін
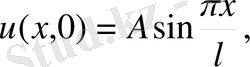
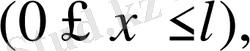
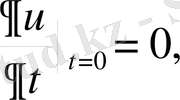
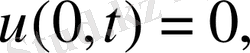
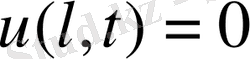
алғашқы және шекаралық шарттары бойынша интегралдау керек.
Сонда (2. 42) және (2. 43) формулалар арқылы
 болады да, ал
болады да, ал
 үшін мынадай өрнек алынады:
үшін мынадай өрнек алынады:
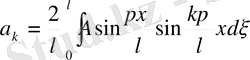
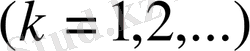
Бұл интеграл
 мәнінен басқа мәндерінде нөлге тең болады.
мәнінен басқа мәндерінде нөлге тең болады.
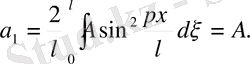
Олай болса есептің шешімі мынаған тең болады.
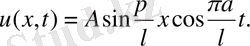
20-мысал.
Шеттері
 және
және
 нүктелерінде бекітілген шекті кішкене балғамен ұрғанда оның
нүктелерінде бекітілген шекті кішкене балғамен ұрғанда оның
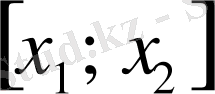 бөлігінің нүктелері
бөлігінің нүктелері
 жылдамдық алады. Ұрғанға дейін шек тепе-теңдік күйінде болатын. Шектің
жылдамдық алады. Ұрғанға дейін шек тепе-теңдік күйінде болатын. Шектің
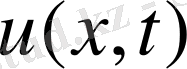 ауытқуын табу керек.
ауытқуын табу керек.
Шешуі: Бұл жағдайда
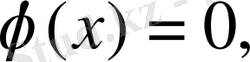
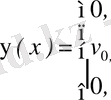
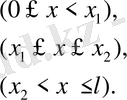
Сондықтан (2. 43) формула бойынша
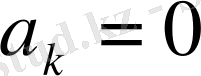 болады.
болады.
Енді
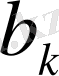 - ны есептейміз.
- ны есептейміз.
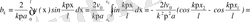
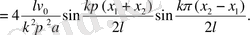
Есептің шешімі
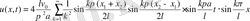
21-мысал.
Шеттері
 және
және
 нұктелерінде бекітілген шек
нұктелерінде бекітілген шек
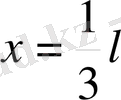 нүктесінде тепе-теңдік күйінен
нүктесінде тепе-теңдік күйінен
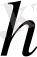 аз қашықтыққа керіледі де бастапқы жылдамдықсыз босатылып жіберіледі. Шектің
аз қашықтыққа керіледі де бастапқы жылдамдықсыз босатылып жіберіледі. Шектің
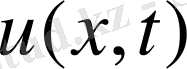 ауытқуын табу керек.
ауытқуын табу керек.
Шешуі: Бұл жағдайда

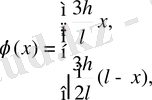
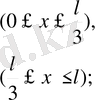
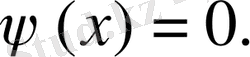
Осыдан
 , ал
, ал
 мәнін есептейміз:
мәнін есептейміз:
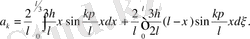
Мұндағы екі интегралды да бөліктеп интегралдау нәтижесінде мынадай
 мәнін анықтаймыз:
мәнін анықтаймыз:
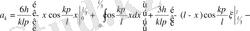
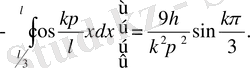
Сонымен,
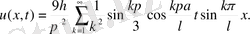
22-мысал.
Бір шеті бекітілген, ал екінші шеті бос цилиндр стерженнің бойымен таралған шағын тербелістерді интегралдау керек.
Шешуі: Стреженнің бойымен таралған тербелістер теңдеуі
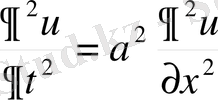 (2. 73)
(2. 73)
Мұндағы
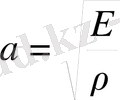 , Е- Юнг модулі,
, Е- Юнг модулі,
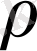 - сызықтық тығыздық.
- сызықтық тығыздық.
Алғашқы шарттар
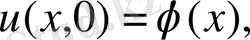
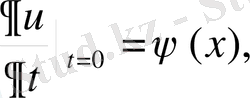
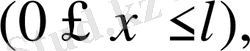 (2. 74)
(2. 74)
түрінде берілсін.
Есептің берілуі бойынша шекаралық шарттарды мына түрде жазуға болады:
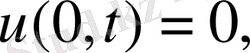
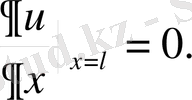 (2. 75)
(2. 75)
Бұрынғы есептердегі шекаралық шарттардан бұл шарттар басқаша.
Сондықтан (2. 42), (2. 43) формулаларды пайдалана алмаймыз.
Енді Фурье әдісінің жалпы түрін пайдаланайық. Алдымен (2. 73) теңдеудің тек қана (2. 74) шарттары қанағаттарндыратын шешімін
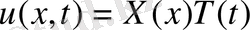
көбейтіндісі түрінде іздейік.
Осыны (2. 73) теңдеуге қойып және айнымалыларын бөлгеннен кейін мынадай теңдеу аламыз.
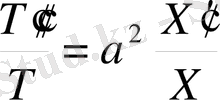
Бұл теңдіктің сол жағы
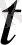 -ға, ал оң жағы тек
-ға, ал оң жағы тек
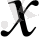 -ке тәуелді. Сондықтан осы тең қатынастардың әрқайсысы тұрақтыға тең болуы керек. Оны
-ке тәуелді. Сондықтан осы тең қатынастардың әрқайсысы тұрақтыға тең болуы керек. Оны
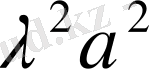 деп белгілеп мынадай диффериенциялдық теңдеулер аламыз.
деп белгілеп мынадай диффериенциялдық теңдеулер аламыз.
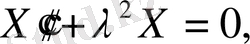
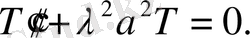
Интегралдаудан кейін мынадай шешімдер аламыз:
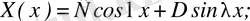
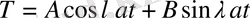 (2. 76)
(2. 76)
Осыдан (2. 76) шартты пайдаланып
С=0,

теңдіктеріне келеміз. Соңғы теңдік бойынша
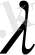 тек мынадай мәндер қабылдай алады
тек мынадай мәндер қабылдай алады
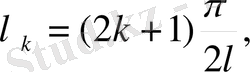
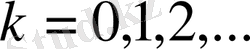
Олай болса, стерженнің меншікті тербелістерінің жиілігі:
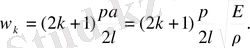
Әрбір
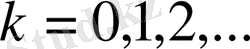 үшін (2. 74) шарттарды қанағаттарндыратын (2. 73) теңдеудің шешімін аламыз
үшін (2. 74) шарттарды қанағаттарндыратын (2. 73) теңдеудің шешімін аламыз
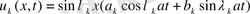
Есептің шешімін қатар түрінде іздейміз:
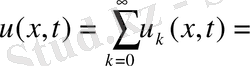
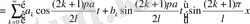 (2. 77)
(2. 77)
Енді
 және
және
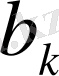 коэффициенттері
коэффициенттері
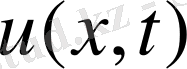 функциясы (2. 74) шарттарды қанағаттандыратындай етіп аламыз ол үшін (2., 77) қатарды (2. 74) -ке қойып белгілі Фурье қатарының коэффициенттерін табу әдісін пайдаланып
функциясы (2. 74) шарттарды қанағаттандыратындай етіп аламыз ол үшін (2., 77) қатарды (2. 74) -ке қойып белгілі Фурье қатарының коэффициенттерін табу әдісін пайдаланып
 және
және
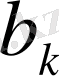 коэффициенттерін анықтаймыз.
коэффициенттерін анықтаймыз.
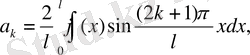
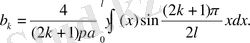
23-мысал.
Мынадай аралас есепті қарастырайық.
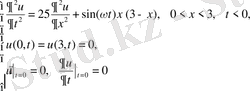 (2. 78)
(2. 78)
Шешуі:
А. Берілген есептің (2. 78) шеттік шарттарының түрімен байланысты есептің шешімін Штурм -Лиувилль есебінің меншікті функциялары бойынша құрылған қатар түрінде іздейміз.
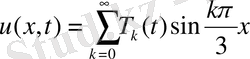 (2. 79)
(2. 79)
Берілген теңдеудегі
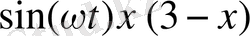 функциясын
функциясын
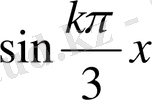 бойынша қатарға жіктейміз.
бойынша қатарға жіктейміз.
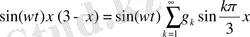 (2. 80)
(2. 80)
Мұндағы
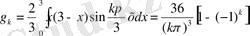
Енді (2. 79) және (2. 80) жіктеулерді (2. 78) теңдеуге қойып мынадай дифференциялдық теңдеу аламыз.
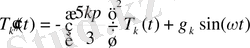 (2. 81)
(2. 81)
((2. 77) теңдеуді қараңыз) .
Ал (2. 79) қатарды (2. 78) алғашқы шарттарға қойғанда
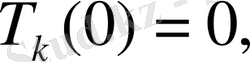
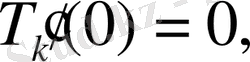 (2. 82)
(2. 82)
шарттары алынады.
Дифференциялдық теңдеулер теориясынан (2. 81) біртекті емес теңдеудің жалпы шешімі оның қандайда бір дербес шешімі мен оған сәйкес біртекті теңдеудің шешімінің қосындысынан тұратыны белгілі.
Сондықтан (2. 81) теңдеудің жалпы шешімін
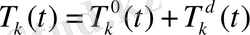 (2. 83)
(2. 83)
түрінде құрамыз.
Мұндағы
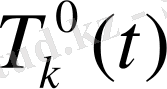 -сәйкес біртекті теңдеудің жалпы шешімі:
-сәйкес біртекті теңдеудің жалпы шешімі:
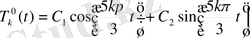 (2. 84)
(2. 84)
Ал
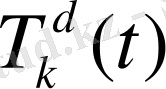 - (2. 81) біртекті емес теңдеудің дербес шешімі.
- (2. 81) біртекті емес теңдеудің дербес шешімі.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz