Көз функцияларының қолданулары және потенциал теориясының элементтері


Лекция 13. Көз функцияларының кейбір қолданулары
- Сфера үшін көз функциясын қолдану әдісі.
- Дөңгелек облыстағы көз функциясы әдісі.
- Жарты кеңістіктегі көз функциясы әдісі.
1. Центрі О, радиусы R сфера үшін көз функциясын құру керек
,
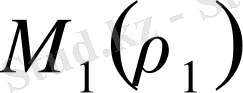
,
,
(1) қатынасында
және
нүктелерінің кері радиус векторлық түрлендірулерін құрамыз. Сфера бетіндегі барлық Р нүктелері үшін
және
нүктелеріне дейінгі қашықтықтары пропорционал
: бұрышы ортақ
немесе
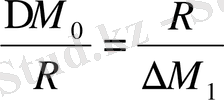
Ұщбұрыш ұқсастығынан
(2)
,
онда
барлық сферада орынды гармоникалық функция
демек
G(P,
 ) =
) =
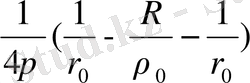 (3) сфера үшін көз функциясы гармоникалық,
(3) сфера үшін көз функциясы гармоникалық,
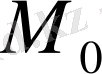 нүктесіндегі ерекшелігі
нүктесіндегі ерекшелігі
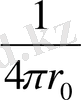 , сферада нөлге айналады.
, сферада нөлге айналады.
Бірінші шеттік есептің шешімі
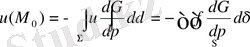
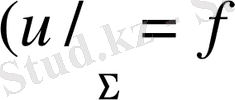 ) (4)
) (4)

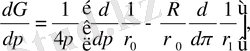 п-сырт нормаль,
п-сырт нормаль,
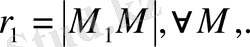
Келтірілген формулалардан
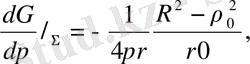 онда
онда
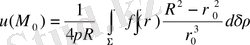 (5)
(5)
Сфералық координаталар енгізсек
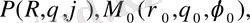
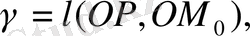 формула (5) мына түрде жазылады.
формула (5) мына түрде жазылады.
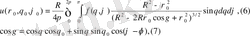
Формула (6) сфера үшін Пуассон интегралы деп аталады.
Сферадан сырт облыс үшін де көрсетілген жолмен көз функциясы құрылады.
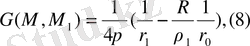
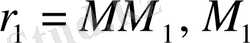 -белгілі нүкте, сферадан тыс жатқан,
-белгілі нүкте, сферадан тыс жатқан,
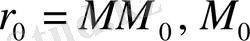 нүктесі
нүктесі
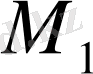 нүктесінен түйіндес,
нүктесінен түйіндес,
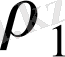 -координаталар басынан
-координаталар басынан
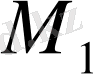 -ге дейінгі аралық.
-ге дейінгі аралық.
Сырттай және іштей есептер нормаль бағыттарынан, кері екендігін ескерсек, сырттай есеп үшін
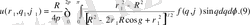
2. Сферада функциясын тапқандай, дөңгелектің көз функциясы табылады. Функцияны мына түрде іздейміз.
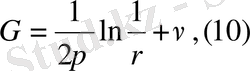
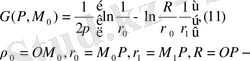
Дөңгелек радиусы.
Осылайша анықталған гармоникалық функция облыс шекарасында нөлге айналады
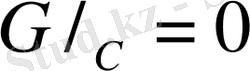 Бірінші шеттік есептің шешімін құруда
Бірінші шеттік есептің шешімін құруда
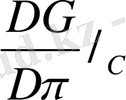 анықталады:
анықталады:
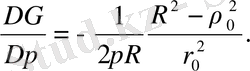 Полярлық координаталарда
Полярлық координаталарда

өрнек (12) дөңгелек үшін Пуассон интегралы деп аталады. Осы формула таңбасы ғана өзгертіліп, сырттай есептің шешімін береді.
3. Шексіздікте регулярды функциялар көмегімен шектеусіз кеңістік көз функциясы енгізіледі Жарты кеңістікте
 көз функциясын анықтайық.
көз функциясын анықтайық.
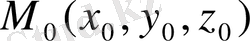 нүктесінің потенциалы
нүктесінің потенциалы
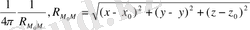 функциясымен анықталады
функциясымен анықталады
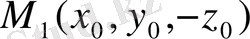 нүктесін қарастырсақ, G функциясы былай анықталады
нүктесін қарастырсақ, G функциясы былай анықталады
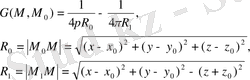
Бұл функция z=0 мәнінде нөлге айналыпб
 - нүктесінде ерекшелігі бар
- нүктесінде ерекшелігі бар
Есептеулер жүргіземіз.
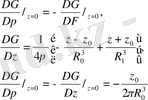
Бірінші шеттік есептің шешімі
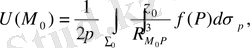 мұндағы
мұндағы
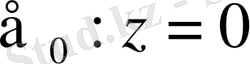 жазықтықтығы,
жазықтықтығы,
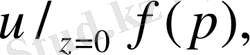 немесе
немесе
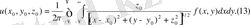
Лекция 14: Потенциал теориясы элементтері.
- Көлемдік потенциалб логарифмдік потенциал
- Меншіксіз интеграл түсініктері
- Көлемдік потенциал туындылары, беттік потенциалдар
- Жәй қабат потенциалының қасиеттері
Функция
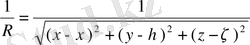
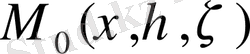 нүктесіне орналасқан бірлік массаның (зарядтың) потенциалының өрісі, Лаплас теңдеуінің
нүктесіне орналасқан бірлік массаның (зарядтың) потенциалының өрісі, Лаплас теңдеуінің
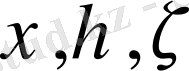 параметрлерінен тәуелді шешімі. Бұл функцияның параметрлері бойынша интегралдары потенциалдар атанып, физикада тікелей қолданысымен қатар, шеттік есептерді шешу әдістерін жетілдірудіе де ерекше орын алады.
параметрлерінен тәуелді шешімі. Бұл функцияның параметрлері бойынша интегралдары потенциалдар атанып, физикада тікелей қолданысымен қатар, шеттік есептерді шешу әдістерін жетілдірудіе де ерекше орын алады.
1.
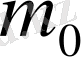 массасы
массасы
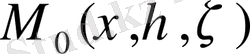 нүктесінде, m массасы M(x, y, z) нүктесінде орналасса, бүкіләлемдік тартылыс заңы бойынша өзара тартылыс күші
нүктесінде, m массасы M(x, y, z) нүктесінде орналасса, бүкіләлемдік тартылыс заңы бойынша өзара тартылыс күші
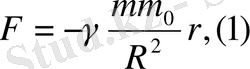
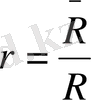 бірлік вектор
бірлік вектор
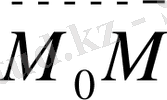
 бағытында,
бағытында,
 -гравитациялық тұрақты. Егер
-гравитациялық тұрақты. Егер
 десек
десек
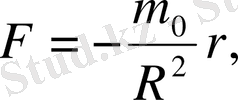 бұл күштің координаталар осьтеріне проекциялары
бұл күштің координаталар осьтеріне проекциялары

Күш өрісінің потенциалын u енгіземіз
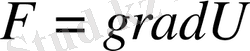 немесе
немесе
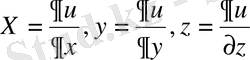 .
.
Бұл жағдайда
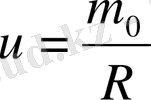 n-материалдық нүкте үшін
n-материалдық нүкте үшін
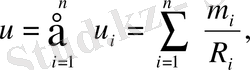 тығыздығы
тығыздығы
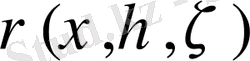 дене Т үшін
дене Т үшін
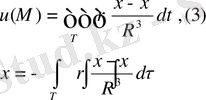
(x, y) координаталарымен берілген жағдайда P(x, y) нүктесінен L сызығының тарту күші
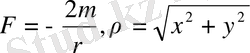 . Бұл күштің потенциалы логарифмдік потенциал деп аталады және
. Бұл күштің потенциалы логарифмдік потенциал деп аталады және
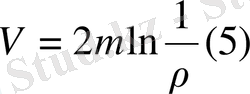 түрінде жазылады. F күшінің компоненттері
түрінде жазылады. F күшінің компоненттері
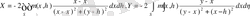 (6)
(6)
потенциалы
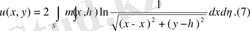
2.
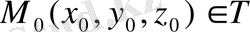 нүктесінде шексіздікке айналатын F(x, y, z) функциясы Тоблысында берілсін
нүктесінде шексіздікке айналатын F(x, y, z) функциясы Тоблысында берілсін
 облысында
облысында
 диаметрі
диаметрі
 -нан аспайтын
-нан аспайтын
 нүктесінің төңірегі (маңайы) анықталған интеграл қарастырамыз.
нүктесінің төңірегі (маңайы) анықталған интеграл қарастырамыз.
Егер
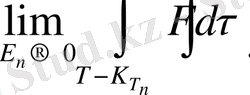 бар болса,
бар болса,
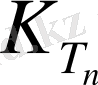 тізбектерін таңдаудан тәуелсіз, онда бұл шек F(x, y, z)
тізбектерін таңдаудан тәуелсіз, онда бұл шек F(x, y, z)
Функциясының Т облысы бойынша меншіксіз интегралы деплып, былай белгіленеді.
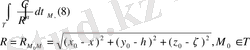
Интегралдарының жинақтылықтарын зерттейік.
Т радиусы R центрі
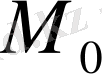 шар делік,
шар делік,
 радиусы
радиусы
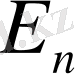 центрі
центрі
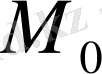 шарлар тізбегі.
шарлар тізбегі.
Онда
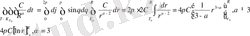
Шекке
 көшсек,
көшсек,
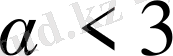 мәндерінде шегі бар,
мәндерінде шегі бар,
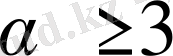 мәндерінде шегі жоқ екендігіне көз жеткіземіз. Сонымен меншіксіз интеграл (8)
мәндерінде шегі жоқ екендігіне көз жеткіземіз. Сонымен меншіксіз интеграл (8)
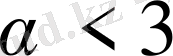 мәндерінде бар, жинақы;
мәндерінде бар, жинақы;
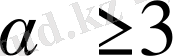 мәндерінде жоқ, жинақы емес.
мәндерінде жоқ, жинақы емес.
Екі айнымалыдан тәуелді интеграл
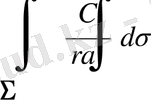
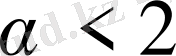 жинақы,
жинақы,
 жинақы емес .
жинақы емес .
Меншіксіз интеграл
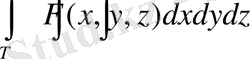 (9) жинақы болуы үшін.
(9) жинақы болуы үшін.
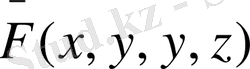 функциясы табылып,
функциясы табылып,
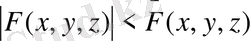 (10) орындалып,
(10) орындалып,
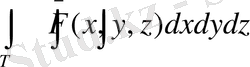 интегралы жинақы болуы жеткілікті. F(M, P) функциясы шексіздікке P=М мәнінде тең болып, теңсіздік орындалса
интегралы жинақы болуы жеткілікті. F(M, P) функциясы шексіздікке P=М мәнінде тең болып, теңсіздік орындалса
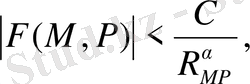
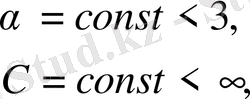
меншіксіз интеграл
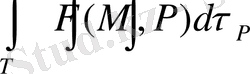 жинақы .
жинақы .
Меншіксіз интегралдарды
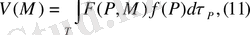
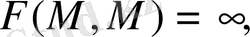 үздіксіз М бойынша,
үздіксіз М бойынша,
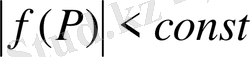 қарастырамыз. Интеграл (11)
қарастырамыз. Интеграл (11)
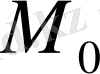 нүктесінде бірқалыпты жинақы, егер
нүктесінде бірқалыпты жинақы, егер
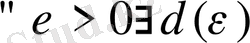
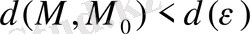 және
және
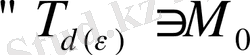 облысында
облысында
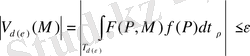 орындалса егер
орындалса егер
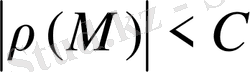 болса
болса
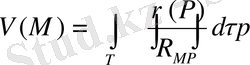 (12) және тарту күшінің компоненттері
(12) және тарту күшінің компоненттері
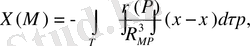
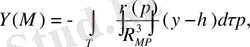
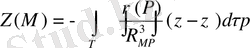 (13) жинақы, себебі
(13) жинақы, себебі
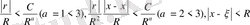
3.
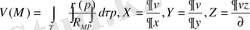 (14)
(14)
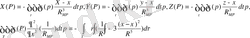 (15)
(15)
Потенциалдың екінші туындысын формалды түрде интеграл астында орындау қате нәтижеге келтіреді. Сондықтан облыстың түрін өзгертіп, интегралды шартты түрде жинақты деп қарастырады.
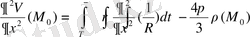 , (16)
, (16)
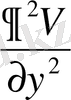 және
және
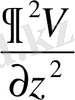 дәл осылай анықталады. Онда
дәл осылай анықталады. Онда
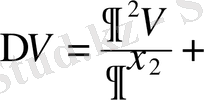
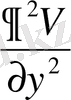 +
+
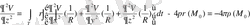
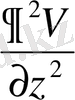
(17) себебі 1/R -гармоникалық функция
Сонымен көлемдік потенциал Пуассон теңдеуінің щешімі
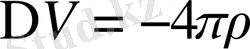 дене ішінде, Лаплас теңдеуінің шешімі
дене ішінде, Лаплас теңдеуінің шешімі
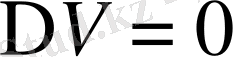 дене сыртында Егер
дене сыртында Егер
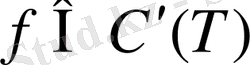 ішкі нүктелер болса, біртекті емес
ішкі нүктелер болса, біртекті емес
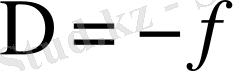 (18) теңдеуінің шешімі
(18) теңдеуінің шешімі
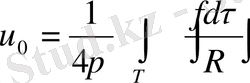
Интеграл
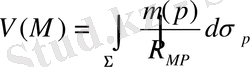 Equation. 3 (19) жәй қабат потенциалы деп аталады. Қос қабат потенциалы деп
Equation. 3 (19) жәй қабат потенциалы деп аталады. Қос қабат потенциалы деп
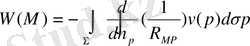 (20) интегралын айтады, немесе
(20) интегралын айтады, немесе
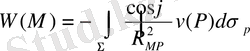 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz