Екінші ретті дербес туындылы дифференциалдық теңдеулер: классификация, канондық түрлері және негізгі шешу әдістері


Қ. А. ЯСАУИ АТЫНДАҒЫ ХАЛЫҚАРАЛЫҚ ҚАЗАҚ-ТҮРІК УНИВЕРСИТЕТІ
ЖАРАТЫЛЫСТАНУ ФАКУЛЬТЕТІ
МАТЕМАТИКА КАФЕДРАСЫ
МАТЕМАТИКАЛЫҚ ФИЗИКА ТЕҢДЕУЛЕРІ
ТҮРКІСТАН, 2012
Екінші ретті дербес туындылы дифференциалдық теңдеулер классификациясы
1. Екі айнымалыдан тәуелді дифференциалдық теңдеулер.
2. Көп айнымалылы екінші ретті дифференциалдық теңеулер
3. Тұрақты коэффицентті тeңдeулердің жәй түрлері.
Белгісіз
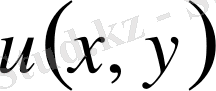 функциясы мен оның екінші реттіге дейінгі дербес туындыларын байланыстыратын
функциясы мен оның екінші реттіге дейінгі дербес туындыларын байланыстыратын
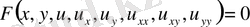 теңдеуі, екінші ретті дербес туындылы дифференциалдық теңдеу деп аталады. Тәуелсіз айнымалылары көп болғанда да теңдеу осы түрде жазылады. Теңдеу
теңдеуі, екінші ретті дербес туындылы дифференциалдық теңдеу деп аталады. Тәуелсіз айнымалылары көп болғанда да теңдеу осы түрде жазылады. Теңдеу
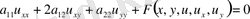 (1)
(1)
жоғарғы ретті туындылары бойынша сызықтық делінеді, мұндағы
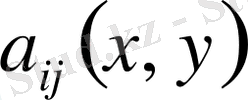 .
.
Егер
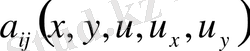 болса, онда теңдеу
квазисызықтық
деп аталады.
болса, онда теңдеу
квазисызықтық
деп аталады.
Теңдеу жоғарғы ретті туындылары
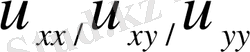 , бойынша да, сондай-ақ функция u және бірінші ретті туындылары
, бойынша да, сондай-ақ функция u және бірінші ретті туындылары
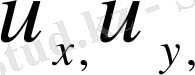 бойынша да, яғни сызықтық
бойынша да, яғни сызықтық
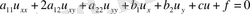 (2)
(2)
турінде болса,
сызықтық
деп аталады, мұнда
 ,
,
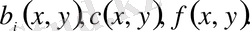 .
.
 Егер коэффиценттері
Егер коэффиценттері
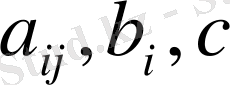 тұрақты болса, теңдеу
тұрақты коэффициентті
деп аталады. Кері түрлендірулері мүмкін болатын
тұрақты болса, теңдеу
тұрақты коэффициентті
деп аталады. Кері түрлендірулері мүмкін болатын
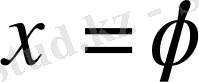
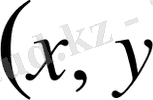 ),
),
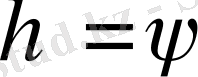
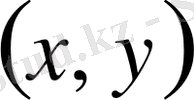 турлендірулерін таңдау жолымен, теңдеуге эквивалентті, жазылу турі жеңіл теңдеуге келеміз.
турлендірулерін таңдау жолымен, теңдеуге эквивалентті, жазылу турі жеңіл теңдеуге келеміз.
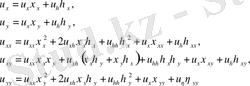 (3)
(3)
Түрлендірулерді (3) теңдеуге (1) қойып, келесі теңдеуді аламыз.
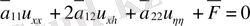 (4)
(4)
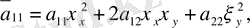
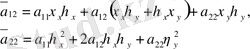
Мұнда
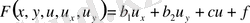 болса, онда
болса, онда
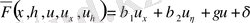 , яғни бастапқы теңдеу сызықты болса, түрлендіруде сол күйі сақталады.
, яғни бастапқы теңдеу сызықты болса, түрлендіруде сол күйі сақталады.
Коэффицент
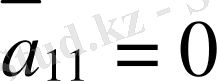 болуы үшін
болуы үшін
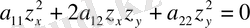 (5)
(5)
теңдеуі қарастырылады.
Лемма
1.
Егер
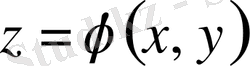 теңдеудің (5) шешімі болса, онда
теңдеудің (5) шешімі болса, онда
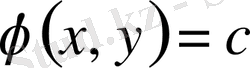 келесі теңдеудің
келесі теңдеудің
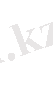
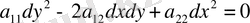
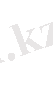 (6)
(6)
жалпы шешімі;
Лемма
2.
Егер
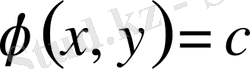 теңдеудің (6) жалпы шешімі болса, онда функция
теңдеудің (6) жалпы шешімі болса, онда функция
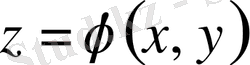 (5) теңдеуді қанағаттандырады.
(5) теңдеуді қанағаттандырады.
Теңдеу (6) бастапқы теңдеудің (1) сипаттаушысы (характеристикалығы), теңдеудің интегралдары оның сипаттаушысы ( характеристикалары) деп аталады.
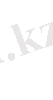
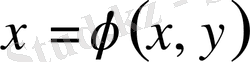 десек
десек
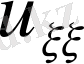 -дің коэффиценті нөлге айналады,
-дің коэффиценті нөлге айналады,
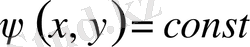 теңдеудің (6) жалпы интегралы болса, онда
теңдеудің (6) жалпы интегралы болса, онда
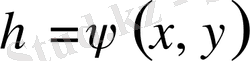 десек
десек
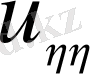 -ның коэффициенті нөлге айналады.
-ның коэффициенті нөлге айналады.
Теңдеу (6) келесі теңдеулерге жіктеледі:
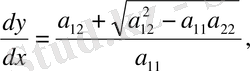 (7)
(7)
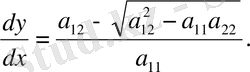 (8)
(8)
Түбір астындағы өрнектің таңбасы теңдеудің
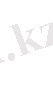
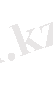
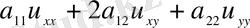
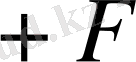
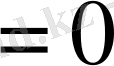 түрін анықтайды.
түрін анықтайды.
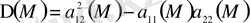
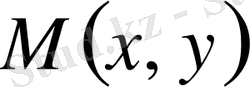 десек, М нүктесінде теңдеу
десек, М нүктесінде теңдеу
1. гиперболалық тектес деп аталады, егер
 >0 болса,
>0 болса,
2. параболық тектес деп аталады, егер
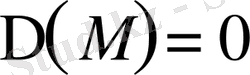 болса,
болса,
3. эллиптикалық тектес деп аталады, егер
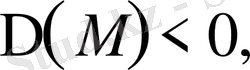 болса
болса
1.
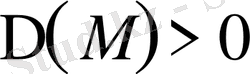 болса,
болса,
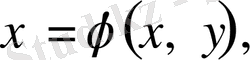
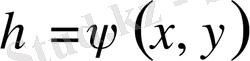 десек, теңдеу
десек, теңдеу
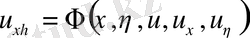 ,
,
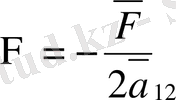 гипербола тектес канондық ( жәй ) түріне келеді.
гипербола тектес канондық ( жәй ) түріне келеді.
Практикада келесі түрдегі канондық теңдеулер де қолданылады. Алмастырулар жасаймыз.
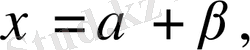
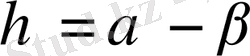 , немесе
, немесе
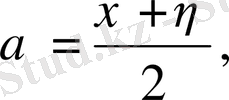
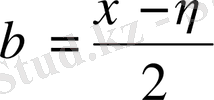 десек теңдеу мына канондық түріне келтіріледі.
десек теңдеу мына канондық түріне келтіріледі.
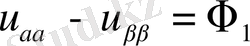

2.
 (M) =0 болса,
(M) =0 болса,
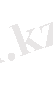
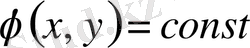 үшін
үшін
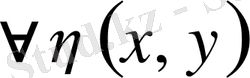 функциясын,
функциясын,
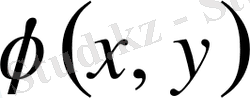 Функциясынан тәуелсіз таңдаған, алмастырулар нәтижесінде парабола тектес теңдеудің канондық түрін аламыз
Функциясынан тәуелсіз таңдаған, алмастырулар нәтижесінде парабола тектес теңдеудің канондық түрін аламыз
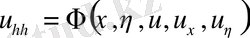
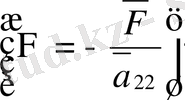 .
.
3.
 <
0, болса,
<
0, болса,
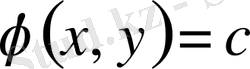 , (7) теңдеудің комплекс интегралы десек,
, (7) теңдеудің комплекс интегралы десек,
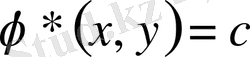 оған түйіндес (8) теңдеу шешімі, онда
оған түйіндес (8) теңдеу шешімі, онда
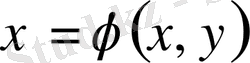 ,
,
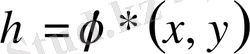 алмастыруларымен
алмастыруларымен
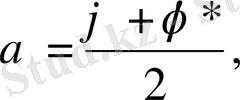
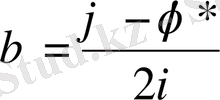 ,
,
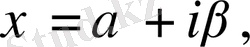
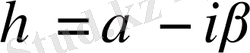 дей отырып, эллиптикалық тектес теңдеудің канондық
дей отырып, эллиптикалық тектес теңдеудің канондық
түрін аламыз.
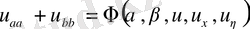
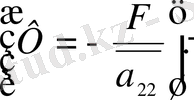
Сонымен
 >0, (гиперб. тектес)
>0, (гиперб. тектес)
 ;
;
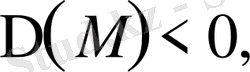 (эллиптик. тектес)
(эллиптик. тектес)
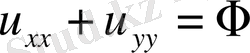 ;
;
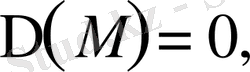 (парабола тектес)
(парабола тектес)
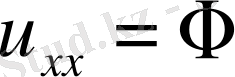 .
.
2. Нақты коэффиценттерімен сызықтық дифференциалдық теңдеуді
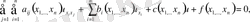 (9)
(9)
келесі түрлендірулермен
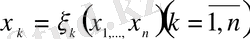 ,
,
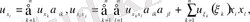
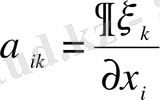 канондық түрге, екі айнымалыдағы әрекеттермен келтіруге болады. Бастапқы теңдеу мына түрге келтіріледі.
канондық түрге, екі айнымалыдағы әрекеттермен келтіруге болады. Бастапқы теңдеу мына түрге келтіріледі.
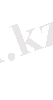
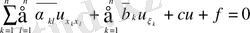
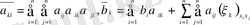 Квадраттық түрлер
Квадраттық түрлер
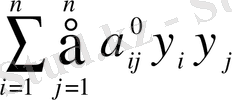 (10) теориясы негізінде теңдеу (9)
(10) теориясы негізінде теңдеу (9)
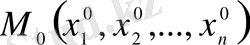
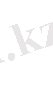 нүктесінде келесі түрлерге келтіріледі.
нүктесінде келесі түрлерге келтіріледі.
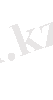
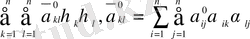 Теңдеу (9)
Теңдеу (9)
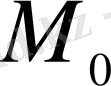 нүктесінде эллиптикалық тектес деп аталады, егер барлық
нүктесінде эллиптикалық тектес деп аталады, егер барлық
 коэффициенттер
коэффициенттер
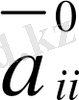 бір таңбалы болса, гиперболалық тектес, егер
бір таңбалы болса, гиперболалық тектес, егер
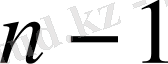 коэффициенттер
коэффициенттер
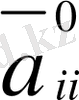 бір таңбалы болып, ал бір коэффициенті оған кері таңбалы болса, ультрагиперболалық тектес, егер
бір таңбалы болып, ал бір коэффициенті оған кері таңбалы болса, ультрагиперболалық тектес, егер
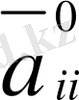 коэффициенттерінің ішінде
коэффициенттерінің ішінде
 коэффициенттері бір таңбалы, қалған
коэффициенттері бір таңбалы, қалған
 коэффициенттері оған кері таңбалы болса,
коэффициенттері оған кері таңбалы болса,
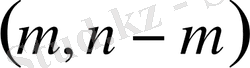
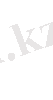 параболалық тектес, егер кем дегенде бір
параболалық тектес, егер кем дегенде бір
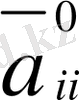 коэффициенті нөлге тең болса
коэффициенті нөлге тең болса
Сонымен
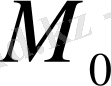 нүктесінде
нүктесінде
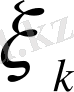 айнымалылары
айнымалылары
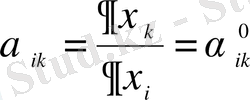 теңдіктерін орындайтын етіп таңдай отырып канондық түрдегі теңдеулерді аламыз.
теңдіктерін орындайтын етіп таңдай отырып канондық түрдегі теңдеулерді аламыз.
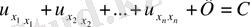 (эллиптикалық тектес)
(эллиптикалық тектес)
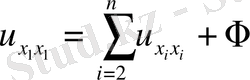 гипербола тектес.
гипербола тектес.
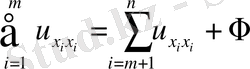 , (
, (
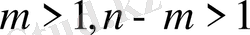 ) ультра гипербола тектес.
) ультра гипербола тектес.
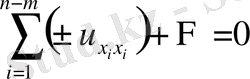 , (
, (
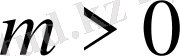 ) параболалық тектес.
) параболалық тектес.
3. Екі айнымалы тұрақты коэффициентті екінші ретті дербес туындылы теңдеу де жоғарыдағыдай канондық түрлерге келтіреді.
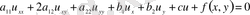 , (11)
, (11)
Сипаттауыш теңдеуінен алынатын сипаттаушылары келесі түзулер болады,
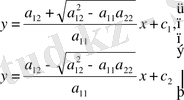 характеристикалық түзулер
характеристикалық түзулер
Сонымен келесі жәй түрлерге лелтіріледі,
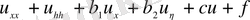 (эллиптикалық), (12)
(эллиптикалық), (12)
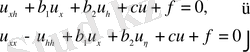 (гиперболалық) (13)
(гиперболалық) (13)
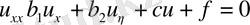 (параболалық ) (14)
(параболалық ) (14)
Лекция 2. Гипербола тектес теңдеуге келтіретін есептер
1. Ішектің жәй көлденең тербелісі.
2. Мембрананың көлденең тербелісі.
3. Шекаралық және бастапқы шарттар.
4. Жалпы есептер құрылымы.
5. Бірғана (жалғыз) шешім теоремасы.
1. Ұзындығы L ішектің t моментіндегі жағдайы
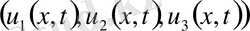 ығысу векторының х нүктесінің t моментіндегі орнымен анықталады. Ішек бір жазықтықта
ығысу векторының х нүктесінің t моментіндегі орнымен анықталады. Ішек бір жазықтықта
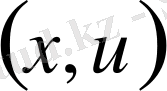 жатады десек, тербеліс үдерісі
жатады десек, тербеліс үдерісі
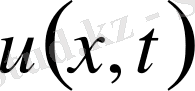 функциясымен анықталады. Ішекті икемді, серпінді деп қарастырамыз. Онда кернеулер дәл моменттегі кескінге жанама бағытында әсер етеді.
функциясымен анықталады. Ішекті икемді, серпінді деп қарастырамыз. Онда кернеулер дәл моменттегі кескінге жанама бағытында әсер етеді.
Сонымен
T(x) =T
 ішекті керу күші. Ньютонның екінші заңы бойынша
ішекті керу күші. Ньютонның екінші заңы бойынша
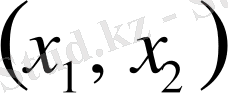 бөлігіндегі қозғалыс шамасы
бөлігіндегі қозғалыс шамасы
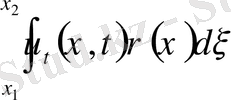 ,
,
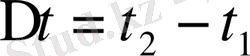 уақыт аралығындағы өзгерісі
уақыт аралығындағы өзгерісі
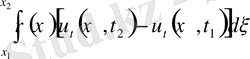 әсер етуші күштерге тең; яғни
әсер етуші күштерге тең; яғни
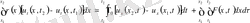 ) (1) . Теңдеу (1) ішектің көлденең тербелісінің интегралдық түрі. U(x, t)
) (1) . Теңдеу (1) ішектің көлденең тербелісінің интегралдық түрі. U(x, t)
 C
C
 дей отырып, интегралдың орта мәні туралы теореманы екі рет, ақырлы өсімшелер теоремасын бірге қолдансақ, ішек тербелісінің дифференциалдық теңдеуін аламыз
дей отырып, интегралдың орта мәні туралы теореманы екі рет, ақырлы өсімшелер теоремасын бірге қолдансақ, ішек тербелісінің дифференциалдық теңдеуін аламыз
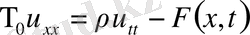 (2) ішектің тығыздығы
(2) ішектің тығыздығы
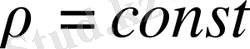 болғанда
болғанда
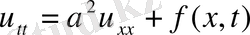
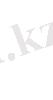
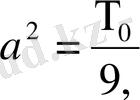 (3),
(3),
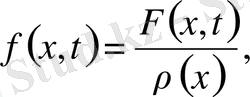 (4) Сыртқы әсер күші жоқ болса
(4) Сыртқы әсер күші жоқ болса
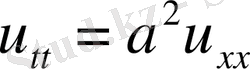 немесе
немесе
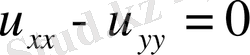 (
(
 ) теңдеуі шығады. х
) теңдеуі шығады. х
 нүктесінде f
нүктесінде f
 (t) шоғырланған күш әсерінде теңдеу (1) мына түрге енеді
(t) шоғырланған күш әсерінде теңдеу (1) мына түрге енеді
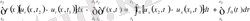 . Бұдан келесі орындалуы тиісті түйіндестік шарттарын аламыз:
. Бұдан келесі орындалуы тиісті түйіндестік шарттарын аламыз:
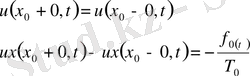
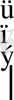
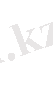 (5)
(5)
2. Иілгіш және ығыстыруға кедергі жасамайтын жазық қолбырды, мембрана деп атайды. C-контурмен шектелген мембрана қарастырылады.
Мембрана үстіндегі
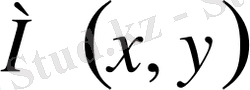 нүктесінен өтетін ds доғасына әсер етуші тарту күші Tds,
нүктесінен өтетін ds доғасына әсер етуші тарту күші Tds,
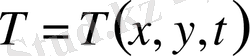 . Сыртқы әсер күші
. Сыртқы әсер күші
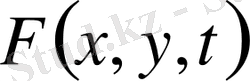 . Қозғалыс шамасының өзгеруін тартылыс күшінің вертикалдық жасаушысы мен сыртқы әсер күшінің қосындысына теңестіріп, мембрана тербелісінің интегралдық түрін аламыз
. Қозғалыс шамасының өзгеруін тартылыс күшінің вертикалдық жасаушысы мен сыртқы әсер күшінің қосындысына теңестіріп, мембрана тербелісінің интегралдық түрін аламыз
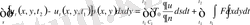 (6),
(6),
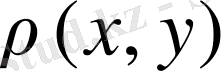 -мембрананың беттік тығыздығы.
-мембрананың беттік тығыздығы.
Дифференциалдық теңдеуге көшу үшін u
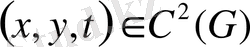 класынан деп, Остроградский теоремасын қолданамыз
класынан деп, Остроградский теоремасын қолданамыз
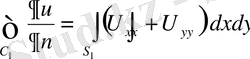 .
.
Онда интегралдық теңдеу (6) келесі түрге келтіріліп
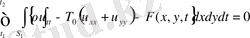 , орта мән туралы теореманың нәтижесінде мембрана тербелісінің дифференциалдық теңдеуін аламыз
, орта мән туралы теореманың нәтижесінде мембрана тербелісінің дифференциалдық теңдеуін аламыз
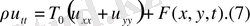 Біртекті мембрана үшін
Біртекті мембрана үшін
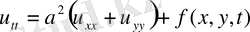
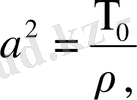 , (8)
, (8)
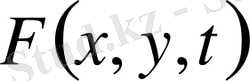 -мембрана массасы бірлігіне бөлінген күш тығыздығы.
-мембрана массасы бірлігіне бөлінген күш тығыздығы.
3. Физикалық есеп дифференциалдық теңдеуге келтірілгенде, үдерісті бір мәнді сипаттау қажеттілігі үшін қосымша шарттар қойылады. Бұл шарттар бастапқы және шекаралық болып келеді.
Ішектің шеткі нүктелері
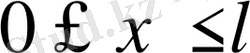 бекітілгенде
бекітілгенде
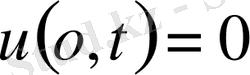 ,
,
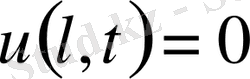 (9) шарттары қойылуы мүмкін. Тербеліс үдерісі ішектің бастапқы жағдайынан тәуелділігі
(9) шарттары қойылуы мүмкін. Тербеліс үдерісі ішектің бастапқы жағдайынан тәуелділігі
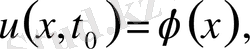
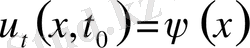 (10) түрінде қойылуы мүмкін, бұлар бастапқы шарттар делінеді. Нақты жағдайға байланысты осы сияқты әртүрлі бастапқы және шекаралық қосымша шарттар қойылады.
(10) түрінде қойылуы мүмкін, бұлар бастапқы шарттар делінеді. Нақты жағдайға байланысты осы сияқты әртүрлі бастапқы және шекаралық қосымша шарттар қойылады.
Негізінен келесі үш түрлі шекаралық шарттар қойылады:
бірінші түрдегі шекаралық шарт
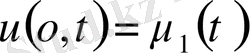
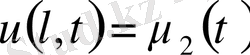 -берілген режим;
-берілген режим;
екінші түрдегі шекаралық шарт
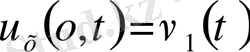 ,
,
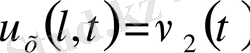 -берілген күш;
-берілген күш;
үшінші шекаралық шарт
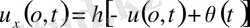 ,
,
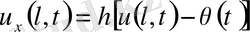 -серпінді бекіту.
-серпінді бекіту.
Күрделі және аралас түрдегі шекаралық шарттар да қойылуы мүмкін.
Шекаралық шарттың түріне байланысты қойылатын есептер шекаралық немесе шеттік есептер деп аталады.
Бірінші шеттік есептің қойылуы:
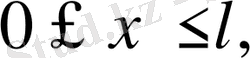
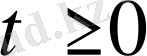 облысында анықталған, теңдеуді
облысында анықталған, теңдеуді
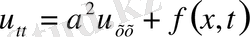
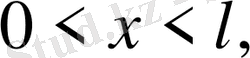
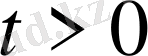 , шекаралық шарттарды
, шекаралық шарттарды
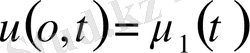
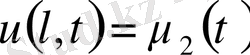
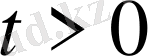 және бастапқы шарттарды
және бастапқы шарттарды
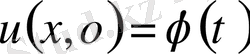 ,
,
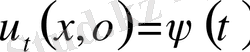
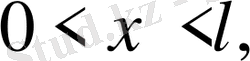 қанағаттандыратын
қанағаттандыратын
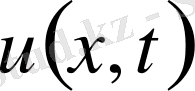 функциясын табу керек.
функциясын табу керек.
Дәл осылайша екінші шекаралық шартпен екінші, үшінші шекаралық шартпен үшінші шеттік есептер қойылады.
Шектеусіз
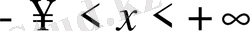 облыста бастапқы шарт ғана берілу мүмкін. Мұндай есепті бастапқы шартты немесе Коши есебі деп атайды: Теңдеудің
облыста бастапқы шарт ғана берілу мүмкін. Мұндай есепті бастапқы шартты немесе Коши есебі деп атайды: Теңдеудің
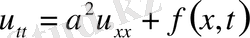 ,
,
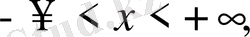
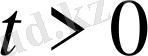 бастапқы шарттарды
бастапқы шарттарды
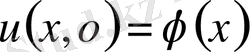 ,
,
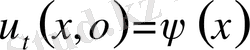 ,
,
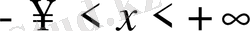 қанағаттандыратын шешімін табу керек.
қанағаттандыратын шешімін табу керек.
Оператор
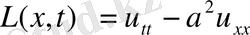 енгізсек, теңдеу L(x, t) =f(x, t) (11) түрінде жазылады. Онда жарты түзу
енгізсек, теңдеу L(x, t) =f(x, t) (11) түрінде жазылады. Онда жарты түзу
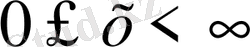 есептері былай қойылуы мүмкін:
есептері былай қойылуы мүмкін:
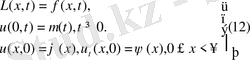 ,
,
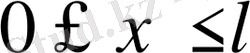
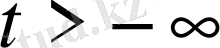 :
:
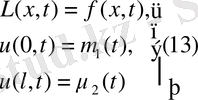 бастапқы шартсыз есеп.
бастапқы шартсыз есеп.
4. Күрделі есепті жәй есептерге жіктеп, жәй есептер шешімдерінен күрделі есеп шешімін құру көп жағдайда тиімді. Жалпы есеп шешімін
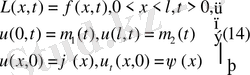 мына түрде іздестіреміз
мына түрде іздестіреміз
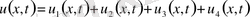 (15), oнда
(15), oнда
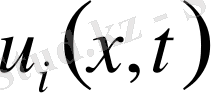 -тер келесі шеттік есептердің шешімдері
-тер келесі шеттік есептердің шешімдері
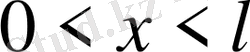 , t>0
, t>0
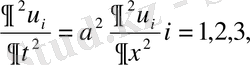
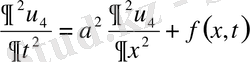
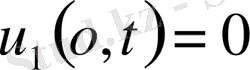 ,
,
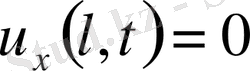 ,
,
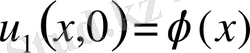 ,
,
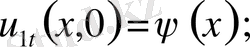
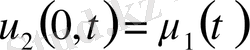
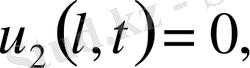
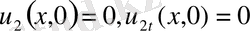 ;
;
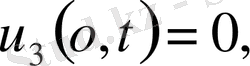
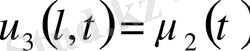 ,
,
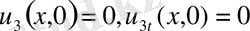 ;
;
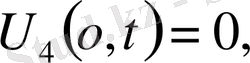
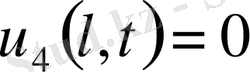 ,
,
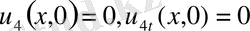
Жалпы шеттік есеп үшін де осындай әрекеттер жасау мүмкін.
Геометриялық айнымалылар саны n>1 болғанда да есептер осылайша қойылады:
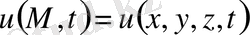 функциясын
функциясын
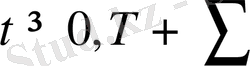 облысы ішінде анықталған,
облысы ішінде анықталған,
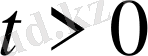 T-ішкі нүктелерінде теңдеуді
T-ішкі нүктелерінде теңдеуді
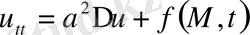
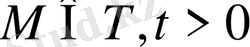 (16) қанағаттандыратын,
(16) қанағаттандыратын,
 шекарасында шекаралық шартты орындайтын
шекарасында шекаралық шартты орындайтын
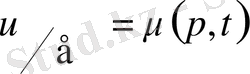
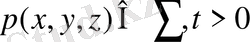 (17) (
(17) (
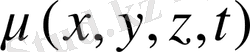 шекарада
шекарада
 берілегн функция) және бастапқы(алғашқы) шарттарды орындайтын
берілегн функция) және бастапқы(алғашқы) шарттарды орындайтын
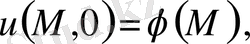
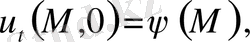 (18) табу керек. Есеп шектеусіз облыстар үшін де осыған ұқсас қойылады.
(18) табу керек. Есеп шектеусіз облыстар үшін де осыған ұқсас қойылады.
5. Бір ғана шешім теоремасы.
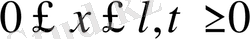 облысында анықталған, теңдеуді
облысында анықталған, теңдеуді
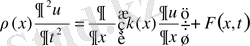
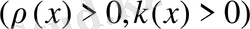
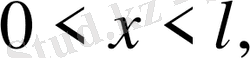
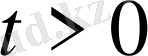 (19) бастапқы және шекаралық шарттарды
(19) бастапқы және шекаралық шарттарды
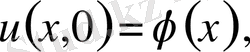
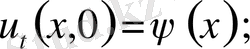
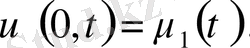
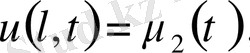 (20)
(20)
қанағаттандыратын бір ғана функцияның бар болуы мүмкін, егер келесі шарттар орындалса:
1) функция
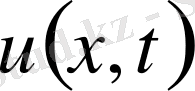 және теңдеудегі (19) туындыларымен бірге
және теңдеудегі (19) туындыларымен бірге
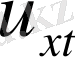 туындысы да
туындысы да
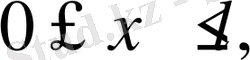
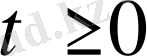 облысында үздіксіз болса;
облысында үздіксіз болса;
2) коэффициенттері
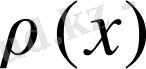 және
және
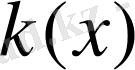 кесіндіде
кесіндіде
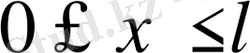 үздіксіз болса.
үздіксіз болса.
Дәлелдеуі
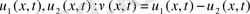 шешімдері делік. Онда
шешімдері делік. Онда
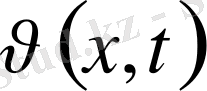 :
:
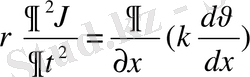 ,
,
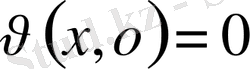 ,
,
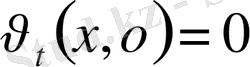 ;
;
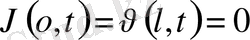 .
.
Функция
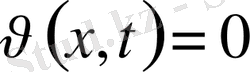 екендігіне көз жеткізелік.
екендігіне көз жеткізелік.
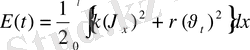 функциясы ішектің t моментігіндегі толық энергиясы.
функциясы ішектің t моментігіндегі толық энергиясы.
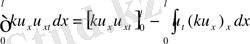
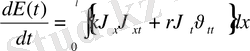 , (
, (
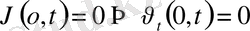 және x=l мәнінде)
және x=l мәнінде)
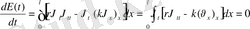 , яғни
, яғни
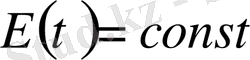 . Бастапқы шарттардан
. Бастапқы шарттардан
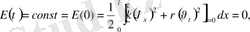 .
.
себебі
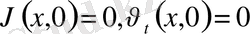
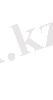 . Соңғы формуладан
. Соңғы формуладан
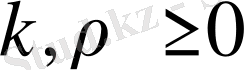 болғандықтан
болғандықтан
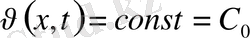 бастапқы шарттан
бастапқы шарттан
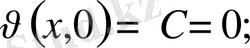 демек
демек
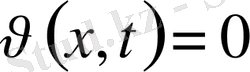 .
.
Егер
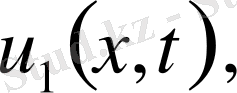
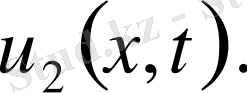 функциялары теорема шарттарын орындаса, онда
функциялары теорема шарттарын орындаса, онда
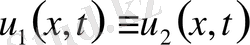 теорема дәлелденді.
теорема дәлелденді.
Лекция 3. Таралатын толқындар әдісі
1. Даламбер формуласы.
2. Біртекті емес теңдеу.
3. Шешімнің орнықтылығы. Қисынды, қисынсыз есептер.
4. Жарты тузу және жалғастыру әдісі.
5. Кесінді есептер.
1. Шектеусіз ішек
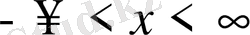 , яғни бастапқы шарттармен қойылған тербеліс теңдеуі есебін қарастырамыз
, яғни бастапқы шарттармен қойылған тербеліс теңдеуі есебін қарастырамыз
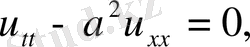 (1)
(1)
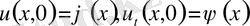 (2)
(2)
Xарактеристикалық теңдеуінің
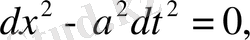

 ,
,
 интегралдары
интегралдары
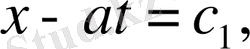
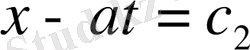 . Жаңа айнымалылар енгізсек
. Жаңа айнымалылар енгізсек
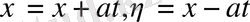 теңдеу (1) мына канондық турге келтіріледі
теңдеу (1) мына канондық турге келтіріледі
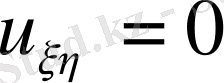 . (3)
. (3)
Бұдан
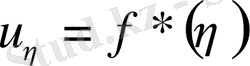
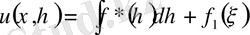
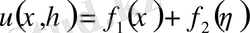 (4)
(4)
Демек
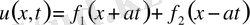 (5)
(5)
теңдеудің (1) жалпы интегралы. Бастапқы шарттардан
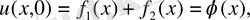 (6)
(6)
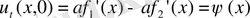 (7)
(7)
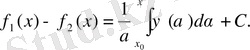
Теңдіктерден
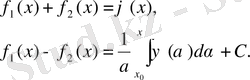
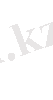
табамыз
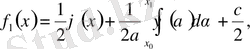
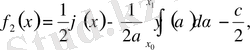
(8)
Табылған
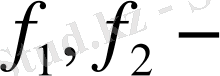 ді (5) теңдікке қоссақ
ді (5) теңдікке қоссақ
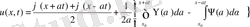
немесе
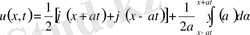 (9)
(9)
Даламбер формуласын аламыз.
Бұл формула
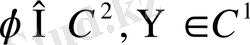 кластарынан алынғанда есептің бір ғана шешімін береді. Шешімді
кластарынан алынғанда есептің бір ғана шешімін береді. Шешімді
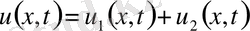 ,
,
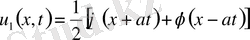 (10)
(10)
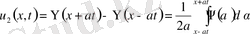 (11)
(11)
түрінде жазуға да болады.
2. Біртекті емес теңдеулер.
Біртекті емес теңдеу үшін Коши есебін қарастырайық.
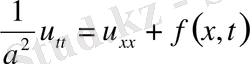 ,
,
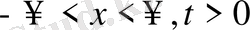 (12)
(12)
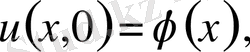
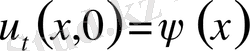
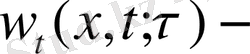 көмекші Коши есебінің шешімі делік
көмекші Коши есебінің шешімі делік
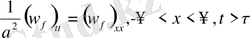 (13)
(13)
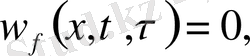
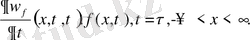 (14)
(14)
Даламбер формуласынан (9)
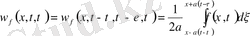 (15)
(15)
Даламбер формуласын (9) мына түрде жазсақ
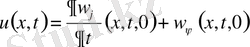 (16)
(16)
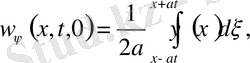
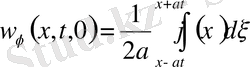
функциялары тиісінше (13) -(14) есептің
 =0, f=
=0, f=
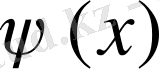 , f=
, f=
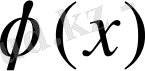 мәндеріндегі шешімдері; себебі тікелей дифференциалдасақ
мәндеріндегі шешімдері; себебі тікелей дифференциалдасақ
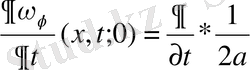
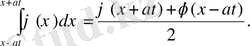
Лемма:
Нөлдік
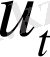 (x, 0) =0, u(x, 0) =0 бастапқы шарттарымен қойылған біртекті емес теңдеудің (12) шешімі
(x, 0) =0, u(x, 0) =0 бастапқы шарттарымен қойылған біртекті емес теңдеудің (12) шешімі
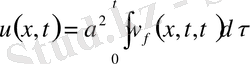 . (17)
. (17)
Есептің(12) шешімі (16) және (17) бойынша
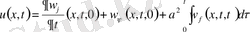 . (18)
. (18)
 үшін (15) өрнектен
үшін (15) өрнектен
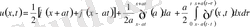 (19)
(19)
Есепке тікелей қою нәтижесінде (19) шешім екендігіне көз жеткіземіз,
егер
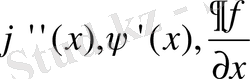 туындылары бар болса.
туындылары бар болса.
3. Теорема
Қандай
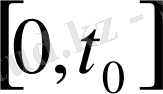 уақыт аралығы және жуықтау дәрежесі
уақыт аралығы және жуықтау дәрежесі
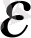 болмасын,
болмасын,
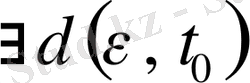 табылып, теңдеудің (1) кез келген екі
табылып, теңдеудің (1) кез келген екі
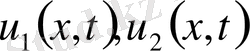 шешімдерінің
шешімдерінің
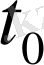 уақыт арасындағы айырымы
уақыт арасындағы айырымы
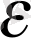 -нан аспайды:
-нан аспайды:
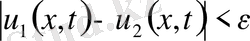 ,
,
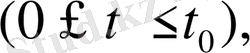 егер бастапқы шарттарының
егер бастапқы шарттарының
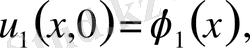
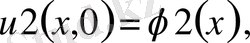
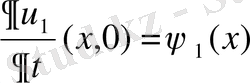 және
және
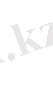
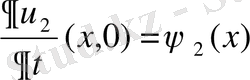
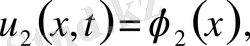
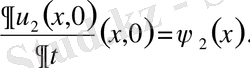
айрымдары
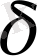 -дан аспаса:
-дан аспаса:
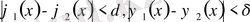
Дәлелдеуі
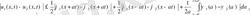 бұдан
бұдан
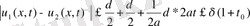 теорема дәлелденеді,
теорема дәлелденеді,
егер
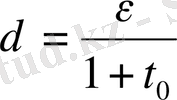 десек. Математикалық есептің шешімі қосымша шарттардан (есептегі бастапқы берілгендерден бастапқы шарттар, шекаралық шарттар және теңдеудің оң жағынан ) үздіксіз тәуелді болса, онда есеп орнықты делінеді.
десек. Математикалық есептің шешімі қосымша шарттардан (есептегі бастапқы берілгендерден бастапқы шарттар, шекаралық шарттар және теңдеудің оң жағынан ) үздіксіз тәуелді болса, онда есеп орнықты делінеді.
Физикалық анықталған құбылыстарға байланысты қисындылық түсінігі енгізіледі. Математикалық есеп қисынды делінеді, егер
- есептің шешімі бар болса,
- есептің бірғана (жалғыз) шешімі болса.
- есептің шешімі бастапқы берілгендерден үздіксіз тәуелді (орнықты) болса.
Аталған шарттардың кемінде біреуі орындалмаса, есеп қисынсыз қойылған делінеді. Практикада қисынсыз қойылған есептер де жиі кездеседі.
Шешімі орнықты емес қисынсыз қойылған есеп мысалын қарастырайық:
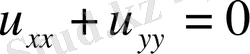 Лаплас теңдеуі
Лаплас теңдеуі
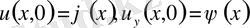
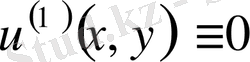 ,
,
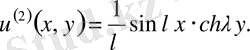 теңдеу шешімдері.
теңдеу шешімдері.
бастапқы шарттары
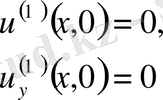
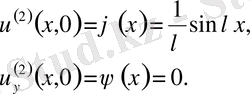
жеткілікті үлкен
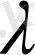 мәндерінде айырымдары өте аз. Бірақ
мәндерінде айырымдары өте аз. Бірақ
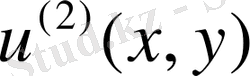 шешімі бұл жағдайда барынша үлкен бола алады. Демек Лаплас теңдеуінің бастапқы шартпен қойыдған есебі қисынсыз.
шешімі бұл жағдайда барынша үлкен бола алады. Демек Лаплас теңдеуінің бастапқы шартпен қойыдған есебі қисынсыз.
4. Жарты түзу және жалғастыру әдісі.
Толқындардың жарты түзуде
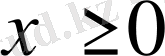 таралуы есептерін қарастырамыз
таралуы есептерін қарастырамыз
Теңдеудің
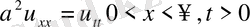 шекаралық шарты
шекаралық шарты
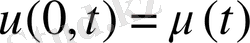 (немесе
(немесе
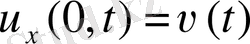 )
)
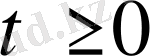
және бастапқы шарттарды
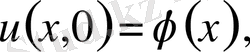
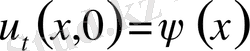
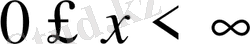
қанағаттандыратын шешімін табу керек.
Алдымен біртекті шекаралық шарттарды
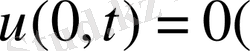 немесе
немесе
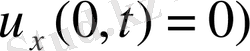 орындайтын есеп шешімін құрамыз.
орындайтын есеп шешімін құрамыз.
шексіз түзу
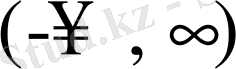 тербеліс теңдеуі шешімінің қасиеттеріне тоқталайық.
Леммалар
тербеліс теңдеуі шешімінің қасиеттеріне тоқталайық.
Леммалар
Лемма1 егер
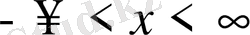 , (1) -(2) есебінің бастапқы шарттары
, (1) -(2) есебінің бастапқы шарттары
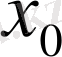 нүктесі бойынша тақ функциялар болса, онда шешімі осы нүктесінде нольге тең. .
нүктесі бойынша тақ функциялар болса, онда шешімі осы нүктесінде нольге тең. .
Лемма
2:
Шексіз түзу есебіндегі бастапқы шарттар
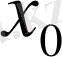 нүктесі бойынша жұп функциялар болса, онда есеп шешімінің туындысы
нүктесі бойынша жұп функциялар болса, онда есеп шешімінің туындысы
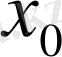 нүктесінде нөлге тең.
нүктесінде нөлге тең.
Леммалар көмегімен келесі есептер шешімдері құрылады.
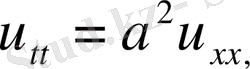
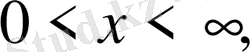
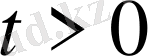
(1-ші шектік есеп) (20)
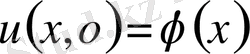
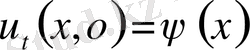
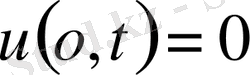
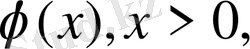 Equation. 3
Equation. 3
 (x) =
(x) =
-
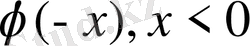 Equation. 3
Equation. 3
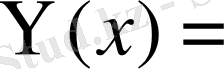
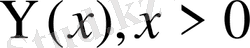 Equation. 3
Equation. 3
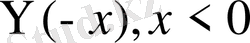 Equation. 3
Equation. 3
функцияларын еңгізіп шексіз түзу есебі шешімін
пайдаланамыз. Онда есеп шешімі
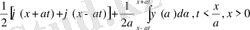
(21)
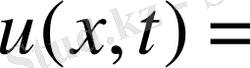
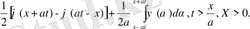
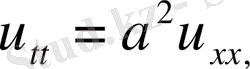
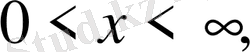
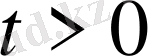 2-ші шектік есеп (22)
2-ші шектік есеп (22)
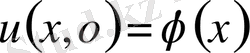
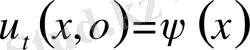
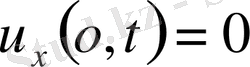
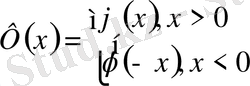
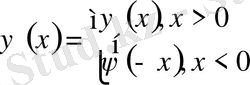 десек шексіз түзу есебінен (22) есеп шешімі құрылады.
десек шексіз түзу есебінен (22) есеп шешімі құрылады.
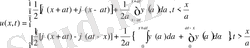 (23)
(23)
Енді
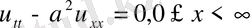
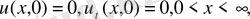 іртекті бастапқы шартты (24) еьінің шешімін құрайық.
іртекті бастапқы шартты (24) еьінің шешімін құрайық.
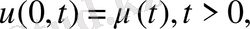
Шешім
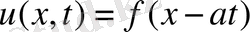 десек, шекаралық шарттан u(0, t) =f(-at) =
десек, шекаралық шарттан u(0, t) =f(-at) =
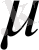 (t), f(z) =(-
(t), f(z) =(-

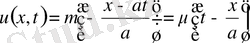 . Бірақ бұл функция
. Бірақ бұл функция
 облысында ғана анықталған, себебі
облысында ғана анықталған, себебі
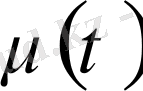
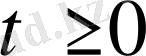 мәндерінде ғана берілген.
мәндерінде ғана берілген.
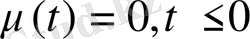 десек
десек
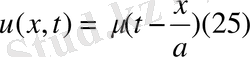 барлық облыста анықталады.
барлық облыста анықталады.
Бұл есептер шешімінен
t
x-at<0
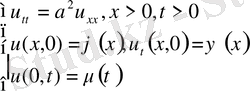 (26)
(26)
x
есебінің шешімі құрылады.
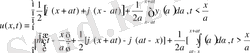 (27)
(27)
5. Кесінді есептері
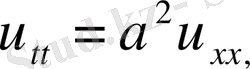
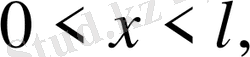
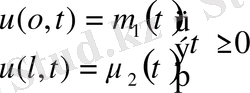 (28)
(28)
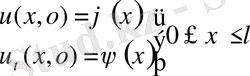
Есептің шешімі жалғастыру әдісімен құрылады
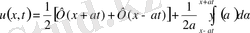
u(x, 0) =Ф(x) =
 (x), u
(x), u
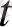 (x, 0) =
(x, 0) =
 (x) =
(x) =
 (x) 0
(x) 0
 x
x
 l
l
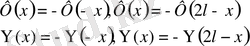
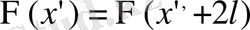
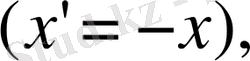
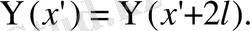
Лекция 4. Айнымалыларды ажырату әдісі
1. Ішектің еркін тербелісінің теңдеуі
2. Тербелістің толқындарға жіктелуі
3. Біртекті емес теңдеулер
1. Айнымалыларды ажырату немесе Фурье әдісі дербес туындылы дифференциалдық теңдеулер есептерін шешудің негізгі әдістерінің бірі болып табылады. Шеттері бекітілген ішектің тербелісі есебін шешеміз.
Сонымен
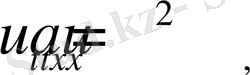 (1)
(1)
есебінің шешімі құрылады.
Алдымен көмекші есеп шешімі
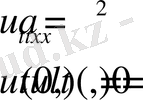 (4)
(4)
көбейтінді түрінде
.
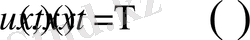 (5)
(5)
құрылады $X^{"}T = \frac{1}{a^{2}}T^{"}X$
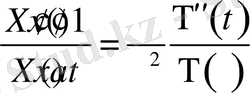 (6)
(6)
Бұдан
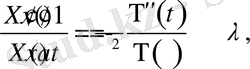 (7)
(7)
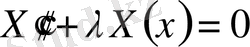 ,
(8)
,
(8)
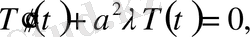 (9)
(9)
шекаралық шарттарынан
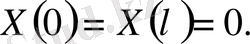 (10)
(10)
қосымша шарты шығады, себебі басқаша десек T(t) 0 және
болар еді.
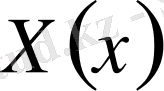 функциясын табу меншікті мәндер есебіне келтіреді: параметр
функциясын табу меншікті мәндер есебіне келтіреді: параметр
 -ның, есептің
-ның, есептің
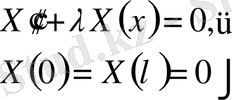 (11) .
(11) .
нөлден өзге шешімдеріне тиісті мәндерін және осы шешімдерін табу керек. Қойылған осы есепті әдетте Штрум-Лиувилль есебі деп атайды.
Жеке жағдайларын қарастырайық.
- , есептің нөлден өзге шешімдері жоқ:
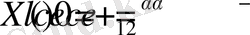
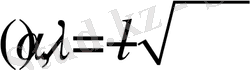
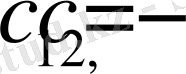
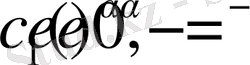


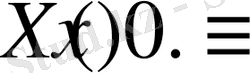
2.
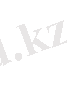
 нөлден өзге шешімдері жоқ:
нөлден өзге шешімдері жоқ:
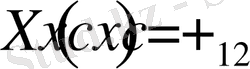 ,
,
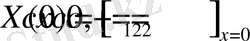
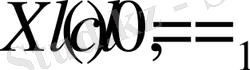

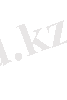
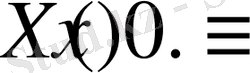
3.
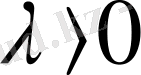
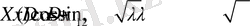
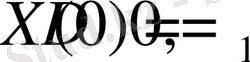
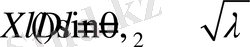
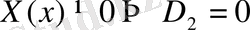
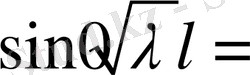 (12)
(12)
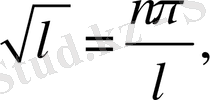
 кез-келген бүтін сан.
кез-келген бүтін сан.
Демек нөлден өзге шешімдер
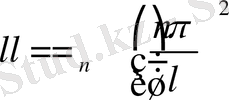 (13)
(13)
мәндерінде ғана бар, яғни
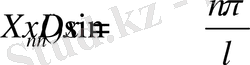 (14)
(14)
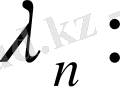
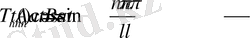 (15)
(15)
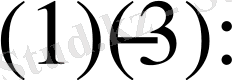
 (16) Теңдеу (1) сызықтық біртекті болғандықтан жеке
(16) Теңдеу (1) сызықтық біртекті болғандықтан жеке
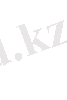
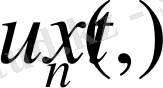 шещімдерінің қосындысы да шешімді береді.
шещімдерінің қосындысы да шешімді береді.
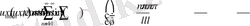 (17)
(17)
Функцияның (17) шарттарды (3) орындауын талап етсек:
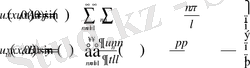 (18)
(18)
Фурье қатарлары теориясы бойынша
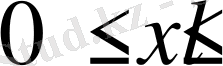 аралығында
аралығында
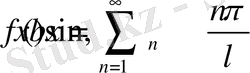 (19)
(19)
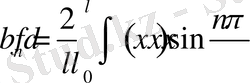 (20)
(20)
 бөліктеп үздіксіз және бөліктеп дифференциалданатын кластан)
бөліктеп үздіксіз және бөліктеп дифференциалданатын кластан)
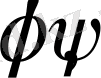 Фурье қатарларына жіктелетін болса
Фурье қатарларына жіктелетін болса
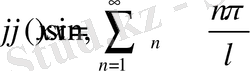
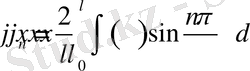 (21)
(21)
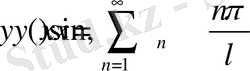
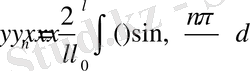 (22)
(22)
бастапқы шарттар орындалуы үшін
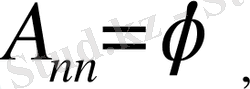
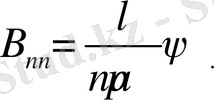 (23)
(23)
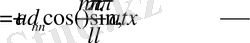 (24)
(24)
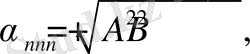
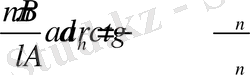 . (25)
. (25)
Әрбір
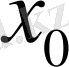 нүктесі гармоникалық тербелістер атқарады.
нүктесі гармоникалық тербелістер атқарады.
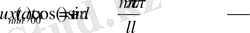 ,
,
амплитудасы
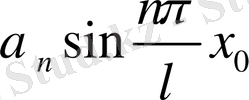 ,
,
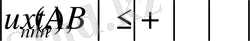
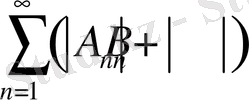 (26)
(26)
Қатар (26) қатар (17) үшін мажорантты. Егер бұл қатар жинақы болса, онда (17) бірқалыпты жинақы, яғни үздіксіз.
 (27)
(27)
мажорантты қатары
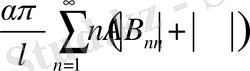 (28)
(28)

мажорантты қатар
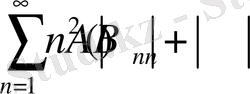
Сонымен
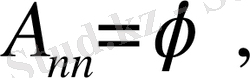
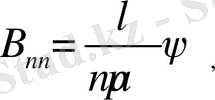
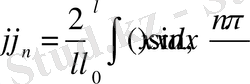
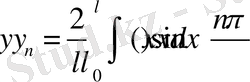
болғандықтан, келесі қатарлардың жинақылықтарын көрсету жеткілікті
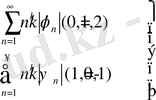 (18)
(18)
Егер 2l периодты
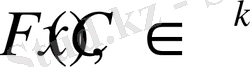 ал
ал
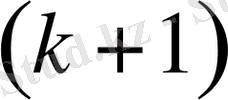 -ретті туындысы бөліктеп-үздіксіз
-ретті туындысы бөліктеп-үздіксіз
болса, онда сан қатары
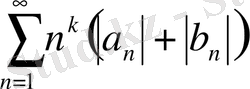 , (19)
, (19)
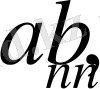 -Фурье коэффициенттері, жинақы.
-Фурье коэффициенттері, жинақы.
Сонымен
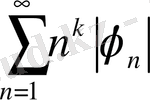
 қатары жинақы, егер талаптар орындалса
қатары жинақы, егер талаптар орындалса
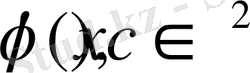
 - бөліктеп-үздіксіз және
- бөліктеп-үздіксіз және
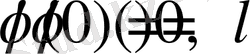
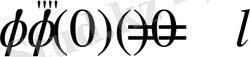
Қатар
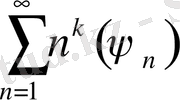
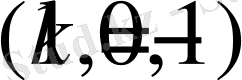 жинақы, егер
жинақы, егер
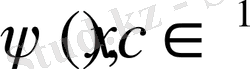
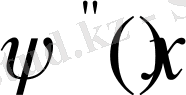 -бөліктеп -үздіксіз және
-бөліктеп -үздіксіз және
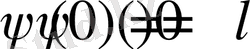 болса.
болса.
3. Тербелістің біртекті емес теңдеуін бастапқы және біртекті шекаралық шарттармен қарастырамыз
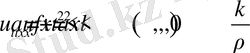 (20)
(20)
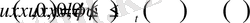 (21)
(21)
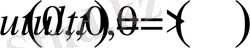 (22)
(22)
Есептің шешімін х бойынша Фурье қатарына жіктеулі түрінде іздестіреміз:
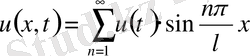 (23)
(23)
Функция
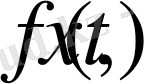 және бастапқы шарттар Фурье қатарына жілтелсе:
және бастапқы шарттар Фурье қатарына жілтелсе:
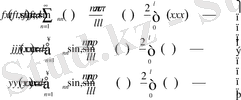 (24)
(24)
Шешімді (23) теңдеуге (20) қойсақ
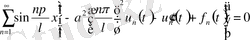
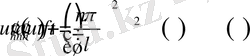 (25) кәдімгі дифференциалдық теңдеуді бастапқы шарттармен аламыз:
(25) кәдімгі дифференциалдық теңдеуді бастапқы шарттармен аламыз:
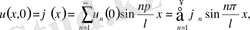
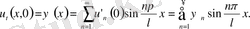
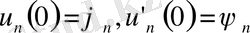 (26) Онда
(26) Онда
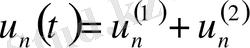 , ал
, ал
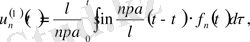 (27) біртекті емес теңдеудің бастапқы шарттары нөл есебінің шешімі де,
(27) біртекті емес теңдеудің бастапқы шарттары нөл есебінің шешімі де,
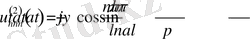 (28)
(28)
бастапқы шарттармен біртекті теңдеудің шешімі. Сонымен ізделініп отырған шешім
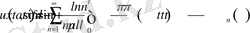
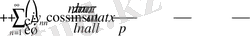 (29)
(29)
немесе
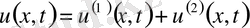 . (29)
. (29)
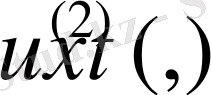 -ішектің еркін тербелісі теңдеуінің бастапқы шарттарымен қойылған есебі бұрын жақсы зерттелген. Енді
-ішектің еркін тербелісі теңдеуінің бастапқы шарттарымен қойылған есебі бұрын жақсы зерттелген. Енді
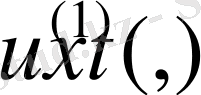 шешімін қарастырайық.
шешімін қарастырайық.

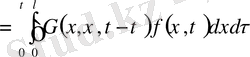 (30)
(30)
 (31)
(31)
Лекция 5. Жалпы бірінші шеттік есеп және айннымалыларды ажыратудың жалпы сызбасы
1. Жалпы бірінші шеттік есеп және стационар біртекті емес есептер.
2. Бастапқы шартсыз есептер.
3. Шоғырланған күш.
4. Жалпы сызба.
1 . Тербеліс туңдеуінің жалпы бірінші шеттік есебін қаралық:
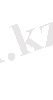
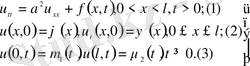
Белгісіз
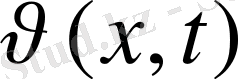 функциясымен, U(x, t) - белгілі деп, шешім u(x, t) құрылады:
функциясымен, U(x, t) - белгілі деп, шешім u(x, t) құрылады:
u(x, t) =u(xt) +
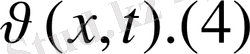
Онда
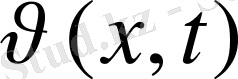 келесі есептің шешімі деп іздестіріледі:
келесі есептің шешімі деп іздестіріледі:
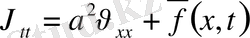 ,
,
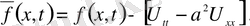
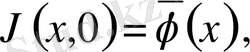
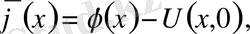
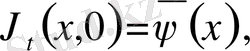
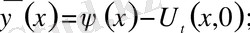
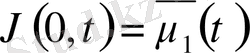
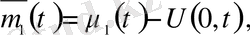
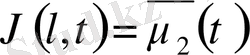
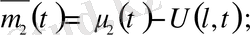
U(x, t) функциясын
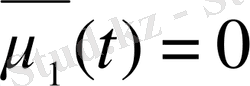 және
және
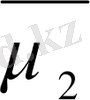 (t) =0 болатындай етіп аламыз, яғни
(t) =0 болатындай етіп аламыз, яғни
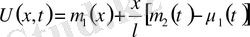
Сонымен u(x, t) үшін жалпы бірінші шеттік есеп, бұған дейін қарастырылған шекаралық шарттары нөл болатын,
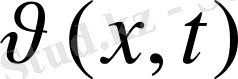 үшін жалпы есепке келтірілді, онда
үшін жалпы есепке келтірілді, онда
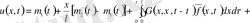
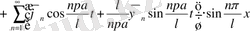 (5)
(5)
Стационар біртекті емес шеттік есептерді қарастырайық
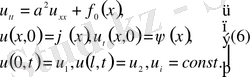
Шешім u(x, t) =
 (x, t) +
(x, t) +
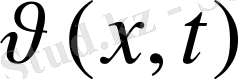 түрінде іздестіріледі,
түрінде іздестіріледі,
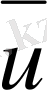 (x) келесі шарттардан анықталады
(x) келесі шарттардан анықталады
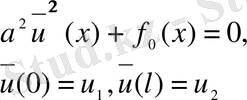 онда
онда
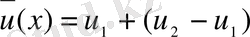
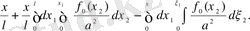
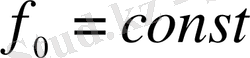 десек, онда
десек, онда
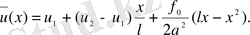
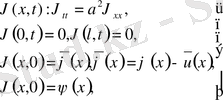
 Мысал.
Мысал.
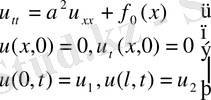 Бұл есепте
Бұл есепте
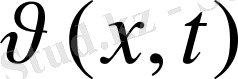 үшін келесі есеп
үшін келесі есеп
алынады:

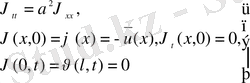
2. Практикада бастапқы шартсыз есептер де жиі кездеседі
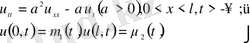
г(l, t) =Acoswt (немесе u(l, t) =Bsinwt), u(0, t) =0 болғанда u(l, t) =Ae
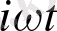 түрінде қарастыру тиімді.
түрінде қарастыру тиімді.
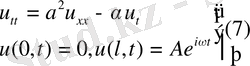 есебінің шешімін табайық.
есебінің шешімін табайық.
u(x, t) =X(x) e
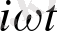 десек:
десек:
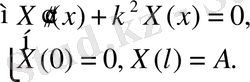
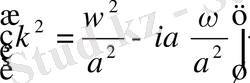 (8)
(8)
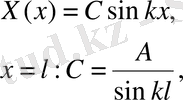
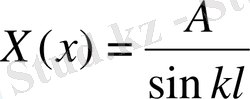
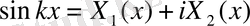 (10)
(10)
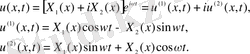
3
.
 нүктесінде f(t) шоғырланған күш әсері бар жағдайды қарастырайық,
нүктесінде f(t) шоғырланған күш әсері бар жағдайды қарастырайық,
онда
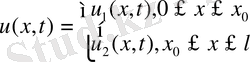
Есеп:
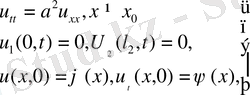 (6)
(6)
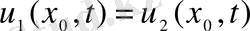 ,
,
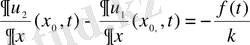
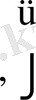 (7) -түйіндестік шарты.
(7) -түйіндестік шарты.
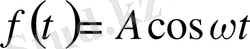 ,
,
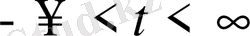 десек, шешім мына түрде іздестіріледі.
десек, шешім мына түрде іздестіріледі.
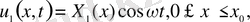
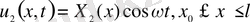 (8)
(8)
Онда:
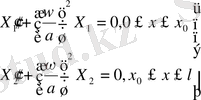 (9)
(9)
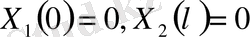 (10)
(10)
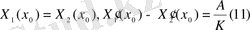
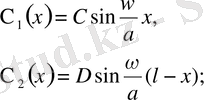
(7) -шарттан:
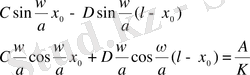
Сонымен
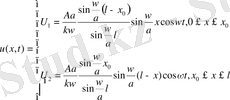 (12)
(12)
Дәл осылайша
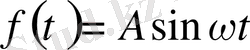 жағдайы шешімі де құрылады. Егер f(t) =
жағдайы шешімі де құрылады. Егер f(t) =
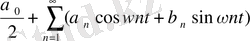 болса, онда шешім:
болса, онда шешім:
 (13)
(13)
4.
Біртекті емес ішек тербелісінің есептеріне де айнымалыларды ажырату әдісі қолданылатынын корсетелік: Теңдеудің L
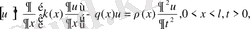 (14)
(14)
берілген шарттарды
u= (0, t) =u(l, t) =0, t
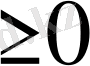 , (15)
, (15)
u(x, 0) =
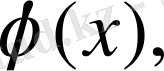
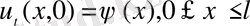 (16)
(16)
орындайтын шешімін табу керек.
Мұндағы k, q,
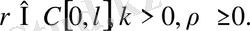
Алдымен (14) теңдеудің (15) шарттарымен шешімі
u(x, t) =X(x) T(t) түрінде ізделінеді.
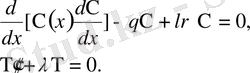
Онда X(x) үшін меншікті мәндер шеттік есебін аламыз:есептің нөлден өзге шешімдері бар болатын
 параметірінің мәндерін және осы шешімдерін табу керек.
параметірінің мәндерін және осы шешімдерін табу керек.
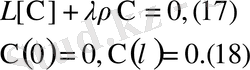
Параметр
 ның мұндай мәндері меншікті мәндер, ал оларға тиісті нөл емес шешімдері (17) -(18) есебінің меншікті функциялары деп аталады.
ның мұндай мәндері меншікті мәндер, ал оларға тиісті нөл емес шешімдері (17) -(18) есебінің меншікті функциялары деп аталады.
Меншікті мәндер (мм) және оларға тиісті меншікті функциялардың (мф) негізгі қасиеттеріне тоқталайық.
1) Саналымды жиын құрайтын
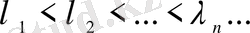 -меншікті мәндер және меншікті функциялар
-меншікті мәндер және меншікті функциялар
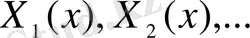 бар.
бар.
2 )
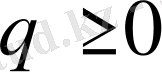 болса барлық
болса барлық
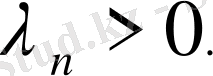
3)
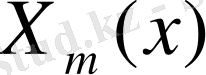 Equation. 3
Equation. 3
 және
және
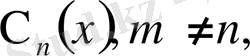 аралықта
аралықта

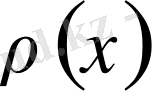 -салмағымен ортогоналды:
-салмағымен ортогоналды:
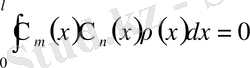
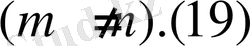
4) (В. А. Стеклов теоремасы )
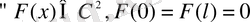 болса, м ф-р
болса, м ф-р
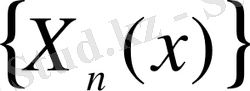 қатарына, бірқалыпты және абсолютті жинақы, жіктеледі:
қатарына, бірқалыпты және абсолютті жинақы, жіктеледі:
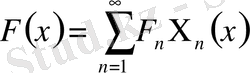 ,
,
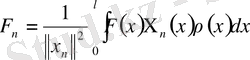 , (20)
, (20)
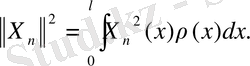
2), 3) қасиеттерді дәлелдеуде Грин формуласы қолданылады:
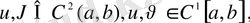
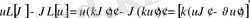 ,
,
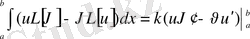
 (21) Грин формуласы.
(21) Грин формуласы.
Енді бастапқы есепке (14) -(16) оралсақ,
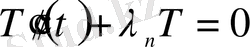 (22)
(22)
теңдеуінен
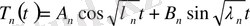 ,
,
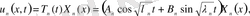
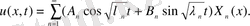 (23)
(23)
Бастапқы шарттардан:
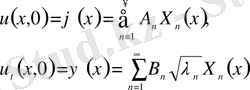

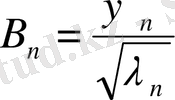 (24)
(24)
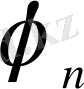 және
және
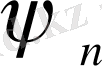 тиісінше
тиісінше
 және
және
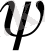 функцияларын
функцияларын
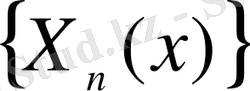 жүйесінде
жүйесінде
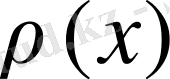 салмағымен Фурье қатарына (20) жіктеу коэффиценттері.
салмағымен Фурье қатарына (20) жіктеу коэффиценттері.
Лекция 6. Гурса есебі, гипербола тектес жалпы сызықтық теңдеулерді шешу
- Есептің қойылуы, тізбектеп жуықтау әдісі
- Туйіндес дифференциалдық операторлар
- Шешімнің интегралдық түрі.
Қосымша берілім харақтеристиқаларында болатын әдетте Гурса есебі аталатын есепті қарастырамыз.
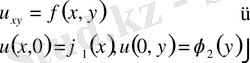 (1)
(1)
Мұнда қосымша берілімдер теңдеудің
 және
және
 характеристикаларында. Функциялар
характеристикаларында. Функциялар
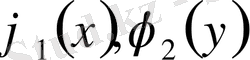 дифференциалданатын және
дифференциалданатын және
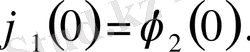 түйіндестік шартын орындайтын, х және у бойынша интегралдасақ.
түйіндестік шартын орындайтын, х және у бойынша интегралдасақ.
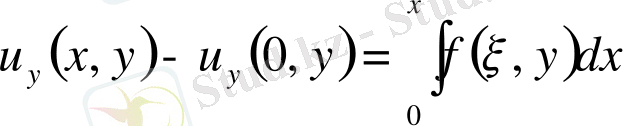
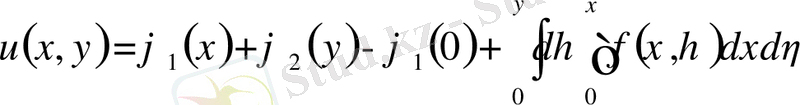 немесе
немесе
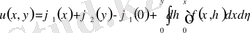 (2)
(2)
Бұл есептің шешімі бар және жалғыз екенідігін көрсетеді. Курделірек сызықтық гиперболалық теңдеу есебін шығарайық.
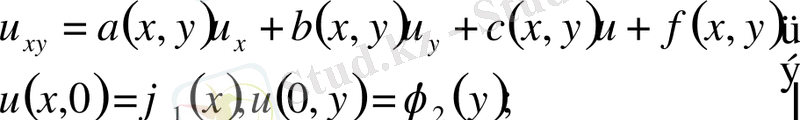 (3)
(3)
Шешімі интеграл-дифференциалдық теңдеуді қанағаттандырады.
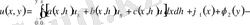
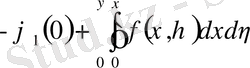 (4)
(4)
Бұл теңдеуді тізбекпен жуықтау әдісімен шешеміз.
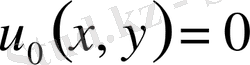 ,
,
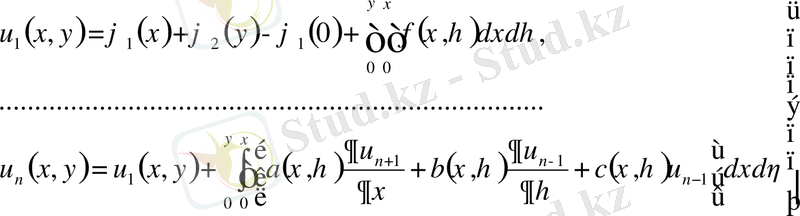 (5)
(5)
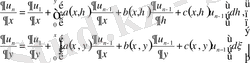 (6)
(6)
Тізбектер
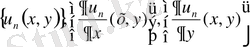 бірқалыпты жинақы екендігін көрсету ушін келесі айырымдарды бағалау қолданылады:
бірқалыпты жинақы екендігін көрсету ушін келесі айырымдарды бағалау қолданылады:
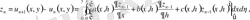
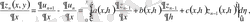
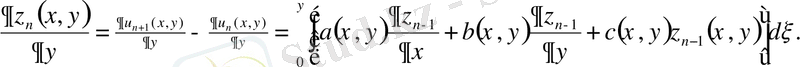
Егер
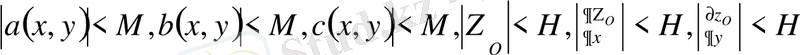 десек,
десек,
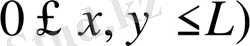 облысында, онда
облысында, онда
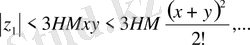
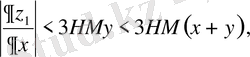
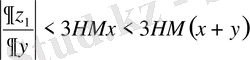
Рекурентті қатынастардан K=L+2 десек:
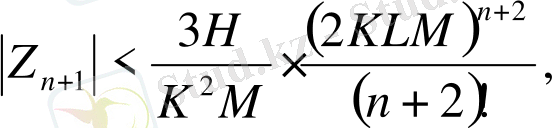
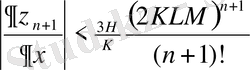 ,
,
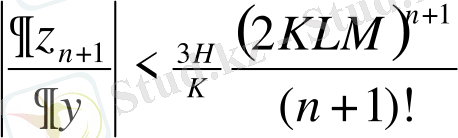 бағалауларың, немесе
бағалауларың, немесе
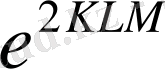 функциясының жіктеуін байкаймыз, немесе тізбектердің
функциясының жіктеуін байкаймыз, немесе тізбектердің
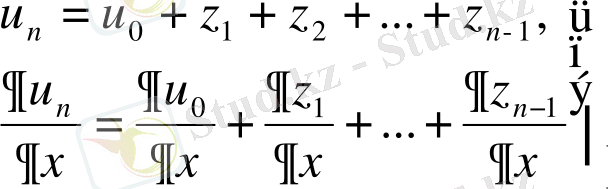
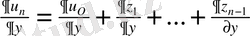
шектеріне бірқалыпты жинақталатынын көреміз
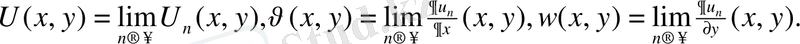 Онда (5), (6) формулалардан:
Онда (5), (6) формулалардан:
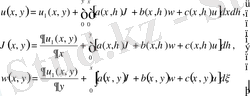 (7)
(7)
Бұдан
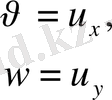 онда
онда
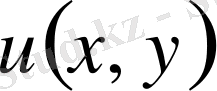 интегро-дифференциалдық теңдеуді (4) қанағаттандыратына көз жеткіземіз.
интегро-дифференциалдық теңдеуді (4) қанағаттандыратына көз жеткіземіз.
2. Шеттік есептер шешімін интегралдық турде жазуға керекті сызықтық дифференциалдық операторларды енгіземіз
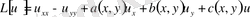 (8)
(8)
(a(x, y), b(x, y), c(x, y) - дифференциалданатын функциялар)
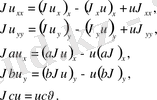
онда
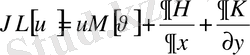 ,
,
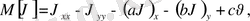
H
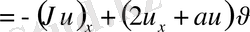 ,
,
K
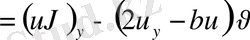 .
.
Дифференциалдық операторлар түйіндес деп аталады, егер
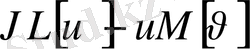
айырымы
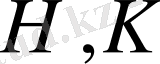 өрнектерінің иісінше х және у бойынша дербес туындыларының қосындысына тең болса. Қаралып отырған операторлар
өрнектерінің иісінше х және у бойынша дербес туындыларының қосындысына тең болса. Қаралып отырған операторлар
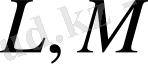 түйіндес. Егер
түйіндес. Егер
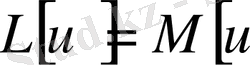 болса, оператор L[u]
өіне-өзі түйіндес
деп аталады. G+C - бөлшектеп - тегіс, облысы берілсе
болса, оператор L[u]
өіне-өзі түйіндес
деп аталады. G+C - бөлшектеп - тегіс, облысы берілсе
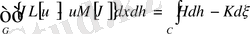 (9)
(9)
екі өлшемді Грин формуласы деп аталады.
3. Келесі есепті (9) формула көмегімен шешеміз: сызықтық гипербола тектес теңдеудің
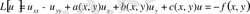 (10)
(10)
бастақы шарттарды С сызығында орындайтын
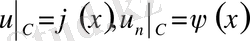 (11´)
(11´)
шешімін табу керек. С:y=f(x) ;
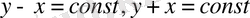
характеристикалары С cызығын бір нүктеден артық қимайтын, яғни
 шарты орындалатындай
шарты орындалатындай
 қисық сызықты ушбұрыш облысында (9) формула былай жазылады:
қисық сызықты ушбұрыш облысында (9) формула былай жазылады:
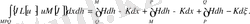
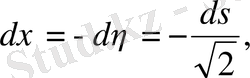 QM;
QM;
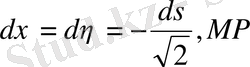
Онда
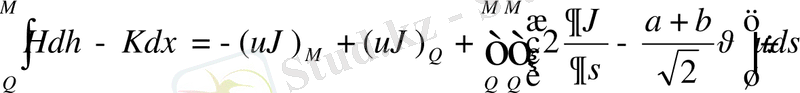
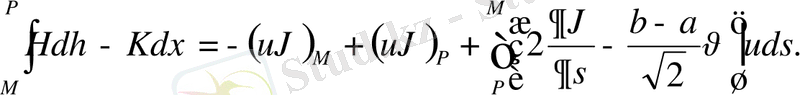
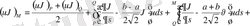
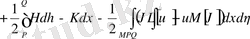 (12)
(12)
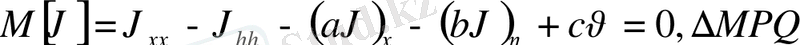 (9)
(9)
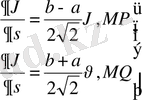 (9а)
(9а)
десек
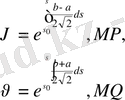
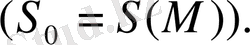
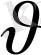 функциясын
Риман функциясы
деп атайды. Сонымен, есептің (10) - (11) шешімі:
функциясын
Риман функциясы
деп атайды. Сонымен, есептің (10) - (11) шешімі:
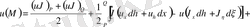
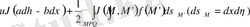 (10)
(10)
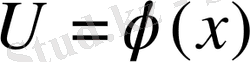
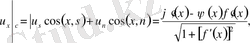
Мысал1.
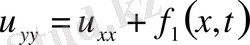
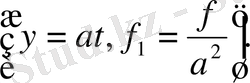 .
.
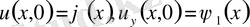
шешуі
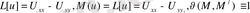
PQ y=0 өсінің кесіндісі. . dy=O PQ,
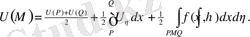
P=P(x-y, o), Q=Q(x+y, o) және бастапқы шарттардан :
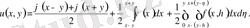
(x, t) айнымалыларына көшсек, Даламбер формуласына ораламыз :
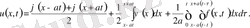
 Мысал 2.
Мысал 2.
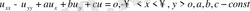
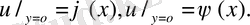
Шешуі. Алмастыру
 жасасақ
жасасақ
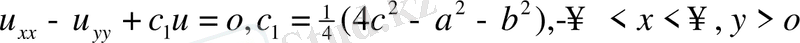
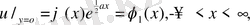
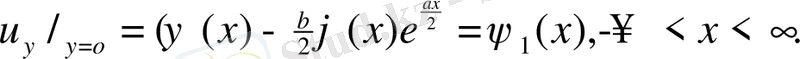
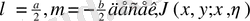 : үшін
: үшін
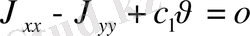
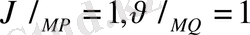
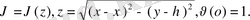
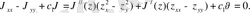
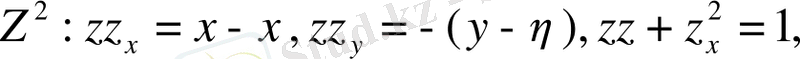
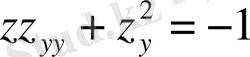
Онда
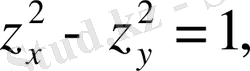
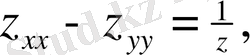
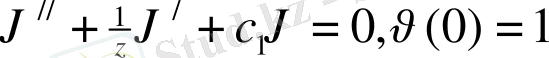
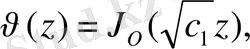
немесе
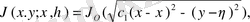
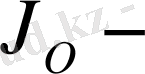 Бессель функциясы,
Бессель функциясы,
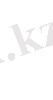
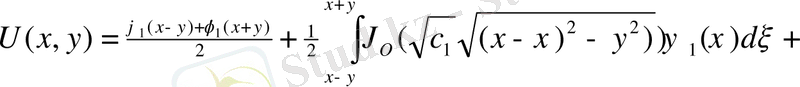
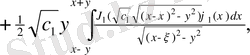
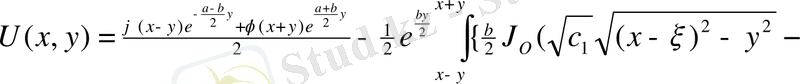
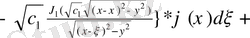
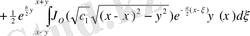
Дербес a=0, b=0 жағдайда
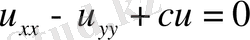
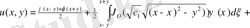
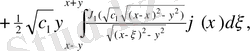
Мұнда
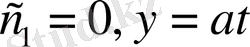 десек, Даламбер формуласына келеміз
десек, Даламбер формуласына келеміз
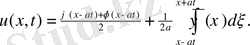
Бұл ішектің тербелісі теңдеуі келесі есебінің шешімі болады.
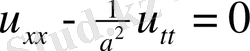
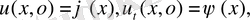
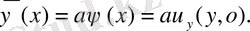
Лекция 7. Парабола тектес теңдеулер есептері
- Жылу таралуының сызықты есебі, диффузия теңдеуі, кеңістікте жылу таралуы есебі.
- Шеттік есептердің қойылуы.
- Жалғыз шешім теоремасы.
Жылу өткізгіштік үдерістерін және диффузияны зерттеуде парабола тектес теңдеулер есептері жиі кездеседі. Парабола тектес ең қарапайым
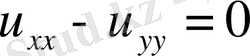
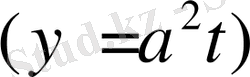 теңдеуі жылу өткізгіштік теңдеуі деп аталады.
теңдеуі жылу өткізгіштік теңдеуі деп аталады.
Ұзындығы l біртекті таяқша (стержень) қарастырылады. Таяқшаның ұштарында және температуралары болса, таяқшаның өнбойында температураның сызықты таралуы орын алады.
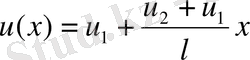 (1)
(1)
Таяқшаның ауданы көлденең қимасынан өтетін жылу мөлшері, уақыт берілгенде
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz