Гетероскедастикалылық: маңызы, салдары, диагностикасы және түзету әдістері


Реферат
Тақырыбы: Гетероскедастикалық
Алматы 2016 ж
Гетероскедастикалық
маңызы және оның салдары.
Ең кіші квадраттар әдісінің алғы шарттарының бірі кездейсоқ ауытқудың тұрақтылық дисперсиясы: Е і кездейсоқ ауытқудың дисперсиясы тұрақты.
Кез келген
і
және
j
бақылаулары үшін:
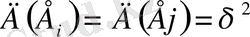
Осындай жағдайлардың пайда болуы гомаскедастикалылық (дисперсия ауытқуының тұрақтылығы) деп аталады. Ал керісінше жағдайда оны гетероскедастикалылық (дисперсия ауытқуының тұрақсыздығы) деп атайды. бар болуын көрнек түрде корелляция өрісінен көруге болады (1-сурет) .
у у у
0 х 0 х 0 х
а) б) в)
мысалдары.
а) х -тің өсуі бойынша қалдықтар дисперсиясы өседі.
б) х айнымалысының орташа мәнінде дисперсия қалдықтары максималды шамасына жетеді және х -тің максималды және минималды мәндерінде азаяды.
в) х -тің аз мәндеріндегі дисперсия қалдықтарының максимал шамасы және х ұлғаюына байланысты дисперсия қалдықтары біртекті.
салдары:
- регрессия теңдеуінің параметрлерін бағалау эффективті емес болады;
- регрессия параметрлерінің стандартты қателеріне баға беру бұрыс болып шығады.
2. байқау.
Ең көп тарағаны Голдфельд-Квандт тесті болып табылады. Бұл тест келесі түрін тексеруге қолданылады: егер
 орташа квадраттық ауытқуы кездейсоқ
і
бақылауындағы
х
і
белгі - факторына пропорционал болса. Бұл жағдайда
Е
і
кездейсоқ жиынтығы нормалды үлестірілген деп болжау жасалады.
орташа квадраттық ауытқуы кездейсоқ
і
бақылауындағы
х
і
белгі - факторына пропорционал болса. Бұл жағдайда
Е
і
кездейсоқ жиынтығы нормалды үлестірілген деп болжау жасалады.
Голдфельд-Квандт алгоритм - тесті төменде келтірілген.
Барлық
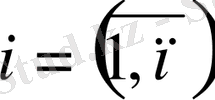 бақылаулар
х
і
мәндері бойынша реттеледі. Бірінші
п
/
бақылау үшін
бақылаулар
х
і
мәндері бойынша реттеледі. Бірінші
п
/
бақылау үшін
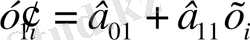
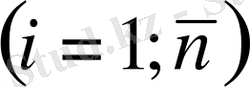 регрессия бағаланады. Ақырғы
п
/
регрессия бағаланады. Ақырғы
п
/
 бақылаулар үшін
бақылаулар үшін
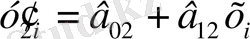
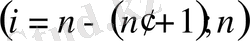 регрессия бағаланады. Белгі - нәтиже мәні фактілік квадраттар сомасының ауытқуынан және оның екі регрессиясы үшін де есеп айыру мәндерімен есептеледі:
регрессия бағаланады. Белгі - нәтиже мәні фактілік квадраттар сомасының ауытқуынан және оның екі регрессиясы үшін де есеп айыру мәндерімен есептеледі:
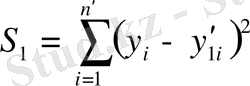 және
және
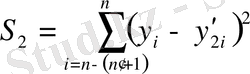
Ауытқу квадраттар сомасының қатынасы есептеледі. Алымында ауытқу квадраттар сомасының көбірегі болу керек. Бұл қатынас
Ғ
үлестіруіне ие болады,
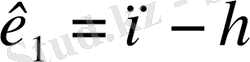 және
және
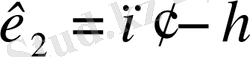 , еркіндік жәрежелерімен,
к
1
=к
2
, мұнда
һ
- регрессия теңдеуіндегі бағаланатын параметрлерінің саны.
, еркіндік жәрежелерімен,
к
1
=к
2
, мұнда
һ
- регрессия теңдеуіндегі бағаланатын параметрлерінің саны.
Егер
Ғ
бақылау
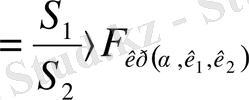 ,
онда орны болады. Егер модельде бірден көбірек факторлар болса, онда бақылаулар сол факторлардан лайықты реттелуі керек, қайсысы қалай болжамданғандай,
,
онда орны болады. Егер модельде бірден көбірек факторлар болса, онда бақылаулар сол факторлардан лайықты реттелуі керек, қайсысы қалай болжамданғандай,
 -мен тығыз байланысқан және
п
/
һ
-тан үлкен болу керек.
-мен тығыз байланысқан және
п
/
һ
-тан үлкен болу керек.
3. жою.
Ол үшін
і
бақылауына ең үлкен салмақ келтіру әдісті табу керек, оның кездейсоқ құрамының орташа квадраттық ауытқуы
 максималды (ондай бақылаулар ең төмен сапаға ие болады) және салмағы төмен орташа квадраттық ауытқу құраушысы
максималды (ондай бақылаулар ең төмен сапаға ие болады) және салмағы төмен орташа квадраттық ауытқу құраушысы
 минималды (мұндай бақылаулар ең жоғарғы сапаға ие) . Ендеше біз регрессия теңдеуінің параметрлерін бағалау дәлірек мәніне ие боламыз:
минималды (мұндай бақылаулар ең жоғарғы сапаға ие) . Ендеше біз регрессия теңдеуінің параметрлерін бағалау дәлірек мәніне ие боламыз:
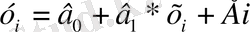 . Теңдеудің оң және сол жақтарын
. Теңдеудің оң және сол жақтарын
 бөлеміз, сонда:
бөлеміз, сонда:
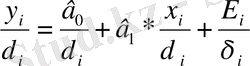 .
.
Жаңа айнымалылар енгізейік:
 .
.
Түрлендірілген теңдеу регрессияның екі факторлық теңдеуіне қатысады (1-ші фактор -
Х
, 2-ші фактор -
υ
) . Бұл теңдеу регрессия (
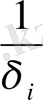 салмағымен) болып табылады. Бұл бақылауда жоғарғы сапалы төменгі
салмағымен) болып табылады. Бұл бақылауда жоғарғы сапалы төменгі
 сапалыға
сапалыға
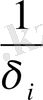 үлкен салмағы беріледі және керісінше
і
бақылауындағы
үлкен салмағы беріледі және керісінше
і
бақылауындағы
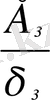 кездейсоқ құрылымы тұрақты дисперсияға ие болады, яғни үлгі гомоскедастикалық болады. жоюды қолдану
кездейсоқ құрылымы тұрақты дисперсияға ие болады, яғни үлгі гомоскедастикалық болады. жоюды қолдану
 фактілік мәндері белгілі болса ғана мүмкін, ал бұл өте сирек кездеседі.
фактілік мәндері белгілі болса ғана мүмкін, ал бұл өте сирек кездеседі.
Бірақ, егер біз кейбір
 мәндерін әрбір
і=1; п
өлшемдерін қолдансақ таңдап алуға болады және екі жағын да
п
бөлсек, гетероскедастикалылық жойылады.
мәндерін әрбір
і=1; п
өлшемдерін қолдансақ таңдап алуға болады және екі жағын да
п
бөлсек, гетероскедастикалылық жойылады.
Мысалға,
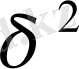 дисперсиясы
х
і
пропорционал деп есептеуге болады.
дисперсиясы
х
і
пропорционал деп есептеуге болады.
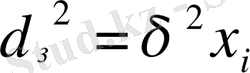 (
(
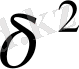 - пропорционалдық коэффициенті) . Онда
- пропорционалдық коэффициенті) . Онда
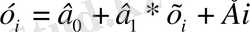 теңдеуді түрлендіру үшін, оның екі жағын да
теңдеуді түрлендіру үшін, оның екі жағын да
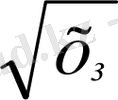 бөлеміз, яғни
бөлеміз, яғни
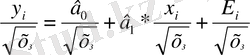 →
→
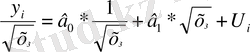
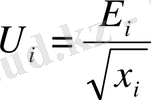 кездейсоқ ауытқулар үшін гомоскедастикалық шарт орындалады. Сондықтан, регрессияға кәдімгі ЕККӘ қолданамыз. Шынында да
кездейсоқ ауытқулар үшін гомоскедастикалық шарт орындалады. Сондықтан, регрессияға кәдімгі ЕККӘ қолданамыз. Шынында да
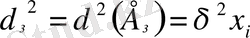 алғышартынан мынау орындалады:
алғышартынан мынау орындалады:
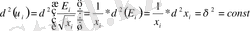
Сөйтіп, ЕККӘ коэффициенттері бойынша
в
0
және
в
1
бағалау арқылы регрессия теңдеуінің бастапқы түріне келеміз:
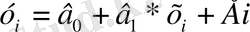 .
.
Егер
 -нің
х
і
деп тәуелділігі квадраттық функция түрінде берілсе, яғни
х
і
2
мәндеріне
-нің
х
і
деп тәуелділігі квадраттық функция түрінде берілсе, яғни
х
і
2
мәндеріне
 дисперсиясының ауытқулары пропорционал болса, онда регрессия теңдеуін
х
і
-
ге бөлеміз (бұл - сәйкестік түрлендіру болады), яғни
дисперсиясының ауытқулары пропорционал болса, онда регрессия теңдеуін
х
і
-
ге бөлеміз (бұл - сәйкестік түрлендіру болады), яғни
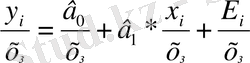
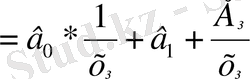
Кездейсоқ құрамдық дисперсия бұл теңдеуде былай жазылады:
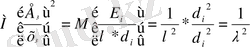 ,
,
яғни ол барлық бақылаулар үшін тұрақты болады, ендеше түрлендірілген регрессия теңдеуінде гетероскедастикалық болмайды.
ЕККӘ-мен коэффициенттері в 0 және в 1 бағалаулардан кейін, регрессия теңдеуі бастапқы түріне келеді.
Классикалық сызықтық регерссия моделін қарастыру барысында ЕКӘ ең жақсы сызықты ығыспаған бағаны береді, егер алғашқы шарттар орындалатын болғанда, солардың бірі ауытқу дисперсиясының тұрақтылығында (гомоскедастикалық) :
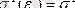
Барлық бақылаулар і бойынша орындалады ( і = 1, 2, . . . , n ) .
Егер бұл алғашқы шарт орындалмағада (гетероскедасткалық жағдайда), ЕКӘ қолдану төменгі жағдайларға келтіріледі. Коэффициенттер бағалар бұрынғыдай ығыспаған және сызықты.
1. Бағалаулар тиімді болмайды (яғни берілген параметрлер бағалауларына қарағанда олар ең кіші дисперсияға ие бола алмайды) . Бағалау дисперсияның өсуі дәл бағалауды алу ықтималдығын кемітеді.
2. Бағалау дисперсиясы ығысу арқылы есептелінеді, регерессия теңдеуімен түсіндірілмеген дисперсия
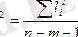 (
m
- түсіндірілетін айнымалылар саны) барлық коэффициенттердің дисперсиясының бағаларын есептеуде пайдалануда ол ығыспаған бағалау бола алмайды.
(
m
- түсіндірілетін айнымалылар саны) барлық коэффициенттердің дисперсиясының бағаларын есептеуде пайдалануда ол ығыспаған бағалау бола алмайды.
3. Жоғарыда айтылғандарға сәйкес, t және F статистикасы бойынша, ол сияқты аралықтар бағалаулар сенімді бола алмайды.
Олай болса, бағалау сапасының стандартын тексерудегі статистикалық көрсеткіштер қате болуы мүмкін, құрылған модельден басқа жағдайларда қате жағдайға келтіреді. Коэффициенттердің стандартты қателіктері төмен болады, олай болса t статистика мәні артуы мүмкін.
Гетероскедастикалық жағдайында ЕКӘ-нің тиімді болмау себебән төмендегі жұптық Ү белгілі бір у і мәнін дисперсиясын тұрақты болмауына сәйкес бір мәні екіншісінен өзгеше болатын өз үлестірімі болатын жиыны жатады.
(у 1 және у n мәндерінің үлестірімін салыстырыңдар) .
ЕКӘ бойынша ауытқу квадраттарының қосындысы
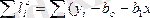
минимумге зерттеледі.
Бұл жағдайда кіші дисперсия үлестірімі (мысалы,
 ) немесе үлкен дисперсия (мысалы,
) немесе үлкен дисперсия (мысалы,
 ) үлестіріміне сәйкес алынғанына қарамастан, берілген қосындыдағы әрбір
) үлестіріміне сәйкес алынғанына қарамастан, берілген қосындыдағы әрбір
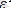 нақты мәндері бірдей «салмаққа» ие болады. Бірақ бұл жағдай қайшылыққа келтіреді, себебі мейлінше аз дисперсия үлестірімімен алынған нүкте регрессия сызығы дәл анықтайды деген тұжырымға сәйкес келмейді.
нақты мәндері бірдей «салмаққа» ие болады. Бірақ бұл жағдай қайшылыққа келтіреді, себебі мейлінше аз дисперсия үлестірімімен алынған нүкте регрессия сызығы дәл анықтайды деген тұжырымға сәйкес келмейді.
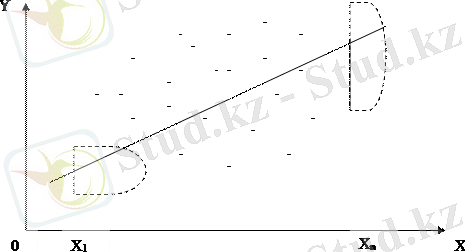
5. 3-сурет
Сонымен үлкен дисперсияға сәйкес келетін үлестіріммен алынған нүктеге қарағанда, ол үлкен «салмаққа ие» болады.
Сондықтан «салмақты» ескеретін бағалау әдісі дәл тиімді бағалауларды алуға мүмкіндік береді.
5. 3. Гетероскедастикалық анықтау
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz