Натурал сандардың бөлінгіштігі: белгілері, қасиеттері және дәлелдері


НАТУРАЛ САНДАР БӨЛІНГІШТІГІ
Ахметжанова А. С.
5А, Ю. А. Гагарин мектеп-лицейі, Ағадыр поселкесі
жетекшісі Сартаева Г. Қ.
Мақсаты. Санның бөлінгіштік белгілерін тез есептеуде, мәтін есептерді шығаруда, дәлелдеуде орынды, жүйелі қолдана білуге қол жеткізу.
Міндеттері.
- Санның бөлінгіштік белгілерін оқып үйрену.
- Бөлінгіштік белгілерін қолданып қандай есептер шығаруға болатынын анықтау.
- Бөлінгіштік белгілерін қолданып есептер шығару.
Өзектілігі . Санның бөлінгіштік белгілері тез есептеуге мүмкіндік беретін болғандықтан, тақырыпты оқып үйрену өмірде уақыт үнемдеуді ұтымды пайдалануға көмектеседі.
Гипотеза . Егер санның бөлінгіштік белгілерін пайдаланып есептеулер жүргізе алса, онда математиканың басқа да салаларын меңгеру әлдеқайда жеңіл болар еді.
Натурал сандар бөлінгіштігі тақырыбы бесінші сынып «Математика» курсынан белгілі. Натурал сандардың бөлгіші, натурал сандардың еселігі ұғымдары осы тақырыпты меңгерудегі негізгі ұғымдар болып табылады. Бір санына кез-келген натурал сан бөлінетіні, ал нөлге ешқандай санды бөлуге болмайтыны мәлім.
Бөлінгіштік белгілері
Бөлінгіштік белгілері деп, берілген х санының а санына қалдықсыз бөлінетінін бөлу амалын орындамай-ақ білуге болатын ережелерді атаймыз.
2-ге бөлінгіштік белгісі.
Егер сан жұп цифрымен аяқталса, сол сан 2-ге бөлінеді
3-ке бөлінгіштік белгісі.
Цифрларының қосындысы 3-ке тең натурал сандар 3-ке бөлінеді.
4-ке бөлінгіштік белгісі.
Егер санның соңғы екі цифрынан құралған сан 4-ке бөлінсе, онда берілген сан да 4-ке бөлінеді.
5-ке бөлінгіштік белгісі .
Жазылуы 0 цифрымен немесе 5 цифрымен аяқталатын натурал сандар 5-ке бөлінеді.
6-ға бөлінгіштік белгісі.
Егер берілген сан 2-ге және 3-ке бөлінсе, онда берілген сан да 6-ға бөлінеді.
7-ге бөлінгіштік белгісі.
Берілген сан 7- ге бөлінетінін білу үшін: ол санды оңнан солға қарай үш - үштен топтаймыз да, тақ нөмірлі санды минуспен, ал жұп нөмірлі санды плюспен жазып, өрнектің мәнін табамыз. Егер өрнектің нәтижесі 7 - ге бөлінсе, онда берілген сан да 7 -ге бөлінеді.
8 -ге бөлінгіштік белгісі.
Егер берілген санның соңғы үш орынды саны 8 -ге бөлінсе, берілген сан да 8 -ге бөлінеді.
9- ға бөлінгіштік белгісі.
Цифрларының қосындысы 9-ға тең натурал сандар 9-ға бөлінеді.
10- ға бөлінгіштік белгісі.
Жазылуы 0 цифрымен аяқталатын натурал сандар 10-ға бөлінеді.
11-ге бөлінгіштік белгісі.
Санның 11-ге бөлінетінін білу үшін: ол санды оңнан солға қарай екі -екіден топтаймыз да қосындысын табамыз. Сонда берілген сан 11- ге бөлінсе, берілген санда 11-ге бөлінеді.
13- ке бөлінгіштік белгісі.
Берілген сан 13- ке бөлінетінін білу үшін: ол санды оңнан солға қарай үш - үштен топтаймыз да тақ нөмірлі санды минуспен, ал жұп нөмірлі санды плюспен жазып, өрнектің мәнін табамыз. Егер өрнектің нәтижесі 13-ке бөлінсе, онда берілген сан да 13-ке бөлінеді.
19- ға бөлінгіштік белгісі.
Сан 19- ға бөлінуі үшін ол санның ондықтары мен екі еселенген бірліктерінің қосындысы 19- ға бөлінуі керек.
25 - ке бөлінгіштік белгісі.
Сан 25- ке бөліну үшін, ол 00, 25, 50, 75, т. с. с. сандардың бірімен аяқталуы керек.
33-ке, 99-ға бөлінгіштік белгісі.
Сан 33-ке, 99-ға бөліну үшін, оның цифрларын оңнан солға қарай екі орыннан бөлгенде шыққан қосындысы 33-ке, 99-ға бөлінуі кеерк.
101-ге бөлінгіштік белгісі.
Егер берілген санның, оңнан солға қарай есептегенде екі -екіден бөлінген цифрларының тақ орындағылардың қосындысы мен жұп орындағылардың қосындысын бірінен -бірін ажыратқанда айырма не 0-ге, не 101 -ге тең болса ол сан 101 -ге бөлінеді.
Анықтама. а натурал саны в натурал санына бөлінеді, егер а=b*c теңдігі орындалатындай с натурал саны табылса.
Сандар бөлінгіштігінің қасиеттері:
- 1) Егер а в және а>0 онда а≥в.
- 2) Егер а в және в а, онда а=в.
- 3) Егер а в және в с, онда а с.
- 4) Егер а с және в с, онда кез келген m және n натурал сандар үшін (ma+nв) c, егер ma> nв болса,
онда (ma-nв) c.
- 5) Егер а в және k≠0, онда ak вk.
- 6) Егер ak вk және k≠0, онда а в.
Есеп:
[ Г. ] 3. 91
Бос торкөзге төмендегі сандарға бөлінетіндей цифр қою керек.
Берілгені: 4758967
- 2 ге, 4758967
- 5 - ке, 4758967
- 3 - ке, 4758967
- 9 - ға, 4758967
- 4 - ке, 4758967
- 25 - ке, 4758967
- 11 - ге, 4758967
[ Г. ] 3. 11
Дәлелдеу керек:
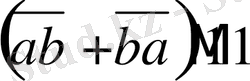
Дәлелдеу:
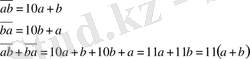
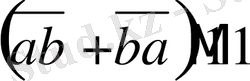 Көбейткіштердің біреуі 11, ендеше 11(a+b) бөлінеді 11-ге, ендеше,
Көбейткіштердің біреуі 11, ендеше 11(a+b) бөлінеді 11-ге, ендеше,
Дәлелденді.
2) Дәлелдеу керек: (
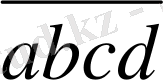 +
+
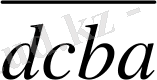 ) бөлінеді 11- ге
) бөлінеді 11- ге
Дәлелдеу:
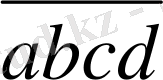 = 1000a+ 100b +10c +d
= 1000a+ 100b +10c +d
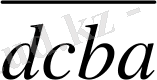 =1000d+100c+10d+a
=1000d+100c+10d+a
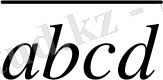 +
+
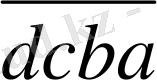 = =1000a+100b+10c+d+1000d+100c+10b+a=1001a+110b+110c+10001d=11*91a+
= =1000a+100b+10c+d+1000d+100c+10b+a=1001a+110b+110c+10001d=11*91a+
+11*10b+11*10c+11*91d=11*(91a+10b+10c+91d)
Көбейткіштердің біреуі 11, ендеше, 11*(91a+10b+10c+91d) көбейтіндісі 11-ге бөлінеді, олай болса, (
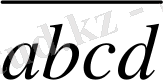 +
+
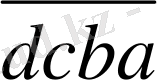 ) бөлінеді 11- ге.
) бөлінеді 11- ге.
Дәлелденді
[ Г. ] 3. 2
а саны 3-ке еселік. Ал b саны 8-ге еселік. а*b саны 24-ке еселік екенін дәлелдеу керек.
Дәлелдеу:
а=3n, b=8n, олай болса
а • b =3n • 8n=24n 2
Көбейткіштердің біреуі 24, ол 24-ке еселік. Ендеше а·b саны 24-ке еселік болады, яғни бөлінеді.
Дәлелденді.
[ Г. ] 3. 3
а бөлінеді 3 -ке, b бөлінеді 2 -ге
Дәлелдеу керек: (2a + 3b) бөлінеді 6-ға
Дәлелдеу: a=3n, b=2n
2a+3b=2*3n+3*2n=6n+6n=12n;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz