Таралатын толқындар әдісі (Лекция 3): Даламбер формуласы, біртекті емес теңдеулер, шешімнің орнықтылығы және жарты түзу мен кесінді есептерін жалғастыру әдісі


Лекция 3. Таралатын толқындар әдісі.
1. Даламбер формуласы.
2. Біртекті емес теңдеу.
3. Шешімнің орнықтылығы. Қисынды, қисынсыз есептер.
4. Жарты тузу және жалғастыру әдісі.
5. Кесінді есептер.
1. Шектеусіз ішек
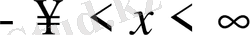 , яғни бастапқы шарттармен қойылған тербеліс теңдеуі есебін қарастырамыз
, яғни бастапқы шарттармен қойылған тербеліс теңдеуі есебін қарастырамыз
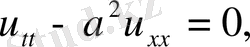 (1)
(1)
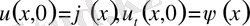 (2)
(2)
характеристикалық теңдеуінің
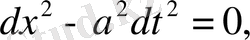

 ,
,
 интегралдары
интегралдары
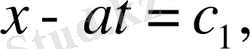
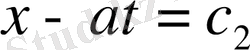 Жаңа айнымалылар енгізсек
Жаңа айнымалылар енгізсек
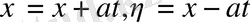 теңдеу (1) мына канондық турге келтіріледі
теңдеу (1) мына канондық турге келтіріледі
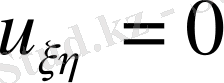 (3)
(3)
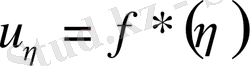
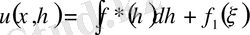
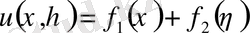 (4)
(4)
Демек
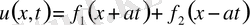 (5)
(5)
теңдеудің (1) жалпы интегралы. Бастапқы шарттардан
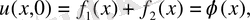 (6)
(6)
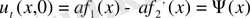 (7)
(7)
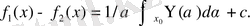
Теңдіктерден
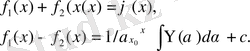
табамыз
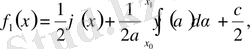
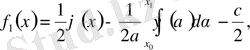 (8)
(8)
Табылған
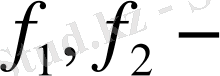 ді (5) теңдікке қоссақ
ді (5) теңдікке қоссақ
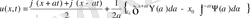
немесе
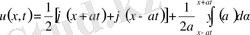 (9)
(9)
Даламбер формуласын аламыз.
Бұл формула
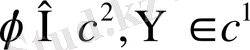 кластарынан алынғанда есептің бір ғана шешімін береді. Шешімді
кластарынан алынғанда есептің бір ғана шешімін береді. Шешімді
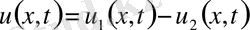 ,
,
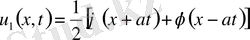 (10)
(10)
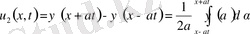 (11)
(11)
Түрінде жазуға да болады.
2. Біртекті емес теңдеулер.
Біртекті емес теңдеу үшін Коши есебін қарастырайық.
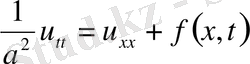 ,
,
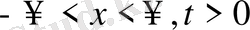 (12)
(12)
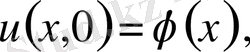
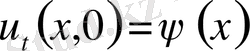
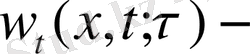 көмекші Коши есебін қарастырайық
көмекші Коши есебін қарастырайық
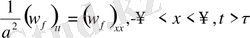 (13)
(13)
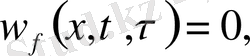
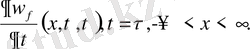 (14)
(14)
Даламбер формуласынан (9)
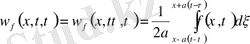 (15)
(15)
Даламбер формуласын (9) мына түрде жазсақ
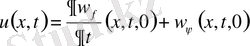 (16)
(16)
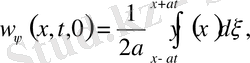
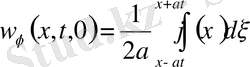
Функциялары тиісінше (13) -(14) есептің n=0, f=
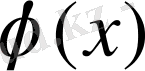 мәндеріндегі шешімдері; себебі тікелей дифференциалдасақ
мәндеріндегі шешімдері; себебі тікелей дифференциалдасақ
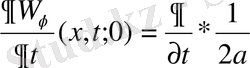
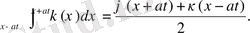
Лемма:
Нөлдік
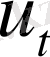 (x, 0) =0, U (x, 0) =0 бастапқы шарттарымен қойылған біртекті емес теңдеудің (12) шешімі
(x, 0) =0, U (x, 0) =0 бастапқы шарттарымен қойылған біртекті емес теңдеудің (12) шешімі
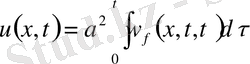 (17)
(17)
есептің(12) шешімі (16) және (17) бойынша
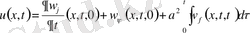 (18)
(18)
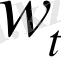 үшін (15) өрнектен
үшін (15) өрнектен
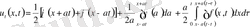 (19)
(19)
Есепке тікелей қою нәтижесінде (19) шешім екендігіне көз жеткіземіз.
Егер
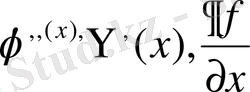 туындылары бар болса.
туындылары бар болса.
3. Теорема
Қандай
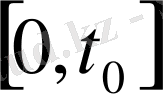 уақыт аралығы және жуықтау дәрежесі
уақыт аралығы және жуықтау дәрежесі
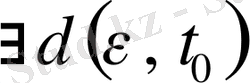 табылып, теңдеудің (1) кез келген екі
табылып, теңдеудің (1) кез келген екі
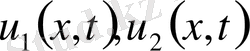 шешімдерінің
шешімдерінің
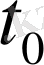 уақыт арасындағы айырымы
уақыт арасындағы айырымы
 -нан аспайды:
-нан аспайды:
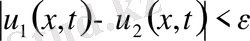 ,
,
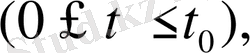 егер бастапқы шарттарының
егер бастапқы шарттарының
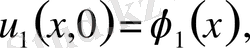
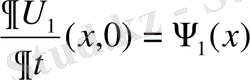 және
және
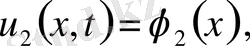
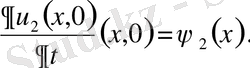
айрымдары
 -дан аспаса:
-дан аспаса:
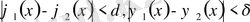
Дәлелдеуі
 бұдан
бұдан
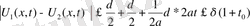 теорема дәлелденеді,
теорема дәлелденеді,
егер
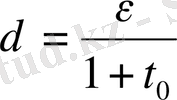 десек. Математикалық есептің шешімі қосымша шарттардан (есептегі бастапқы берілгендерден бастапқы шарттар, шекаралық шарттар және теңдеудің оң жағынан ) үздіксіз тәуелді болса, онда есеп орнықты делінеді.
десек. Математикалық есептің шешімі қосымша шарттардан (есептегі бастапқы берілгендерден бастапқы шарттар, шекаралық шарттар және теңдеудің оң жағынан ) үздіксіз тәуелді болса, онда есеп орнықты делінеді.
Физикалық анықталған құбылыстарға байланысты қисындылық түсінігі енгізіледі. Математикалық есеп қисынды делінеді, егер
- есептің шешімі бар болса,
- есептің бірғана жалғыз шешімі болса.
- есептің шешімі бастапқы берілгендерден үздіксіз тәуелді орнықты болса.
Аталған шарттардың кемінде біреуі орындалмаса, есеп қисынсыз қойылған делінеді. Практикада қисынсыз қойылған есептер де жиі кездеседі.
Шешімі орнықты емес қисынсыз қойылған есеп мысалын қарастырайық:
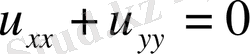 Лаплас теңдеуі
Лаплас теңдеуі
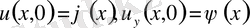
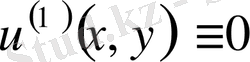 ,
,
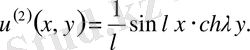 теңдеу шешімдері.
теңдеу шешімдері.
бастапқы шарттары
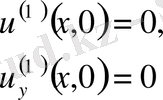
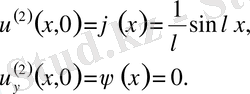
Жеткілікті үлкен
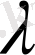 мәндерінде айырымдары өте аз. Бірақ
мәндерінде айырымдары өте аз. Бірақ
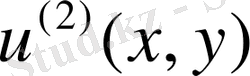 шешімі бұл жағдайда барынша үлкен бола алады. Демек Лаплас теңдеуінің бастапқы шартпен қойыдған есебі қисынсыз.
шешімі бұл жағдайда барынша үлкен бола алады. Демек Лаплас теңдеуінің бастапқы шартпен қойыдған есебі қисынсыз.
- Жарты түзу және жалғастыру әдісі.
Толқындардың жарты түзуде
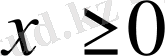 таралуы есептерін қарастырамыз
таралуы есептерін қарастырамыз
Теңдеудің
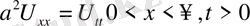 шекаралық шарты
шекаралық шарты
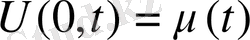 (немесе
(немесе
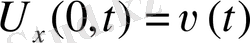 )
)
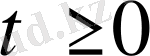
Және бастапқы шарттарды
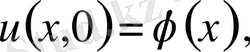
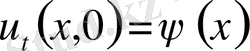
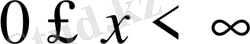
Қанағаттандыратын шешімін табу керек.
Алдымен Біртекті шекаралық шарттарды
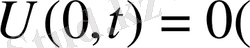 немесе
немесе
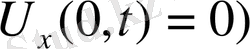 орындайтын есеп шешімін құрамыз.
орындайтын есеп шешімін құрамыз.
шексіз түзу
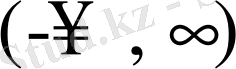 тербеліс теңдеуі шешімінің қасиеттеріне тоқталайық.
Леммалар
тербеліс теңдеуі шешімінің қасиеттеріне тоқталайық.
Леммалар
Лемма1 егер
, (1) -(2) Есебінің бастапқы шарттары
нүктесі бойынша тақ функциялар болса, онда шешімі осы нүктесінде нольге тең. .
Лемма
2:
Шексіз түзу есебіндегі бастапқы шарттар
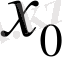 нүктесі бойынша жұп
нүктесі бойынша жұп
Леммалар көмегімен келесі есептер шешімдері құрылады.
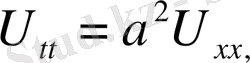
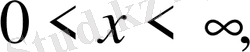
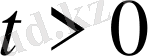
1-ші шектік есеп (20)
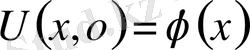
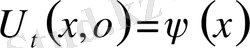
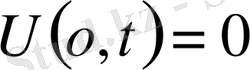
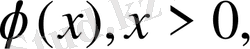 Equation. 3
Equation. 3
Ф(x) =
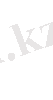 Equation. 3
Equation. 3
-
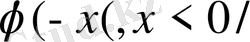 Equation. 3
Equation. 3
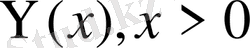 Equation. 3
Equation. 3

-
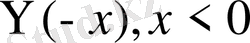 функцияларын еңгізіп шексіз түзу есебі шешімін
функцияларын еңгізіп шексіз түзу есебі шешімін
пайдаланамыз. Онда есеп шешімі
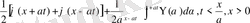
(21)
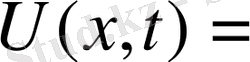
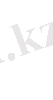
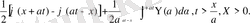
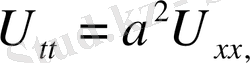
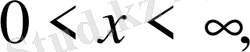
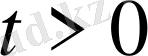 2-ші шектік есеп (22)
2-ші шектік есеп (22)
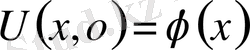
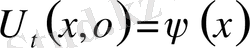
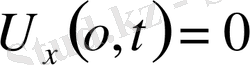
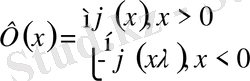
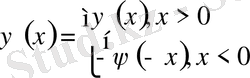 десек шексіз түзу есебінен (22) есеп шешімі құрылады.
десек шексіз түзу есебінен (22) есеп шешімі құрылады.
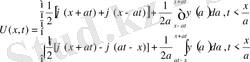 (23)
(23)
Енді
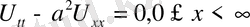
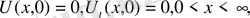 Біртекті бастапқы шартты (24)
Біртекті бастапқы шартты (24)
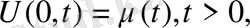
Шешім
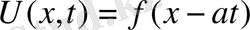 десек, шекаралық шарттан
десек, шекаралық шарттан
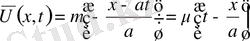 . Бірақ бұл функция
. Бірақ бұл функция
 облысында. Ғана анықталған, себебі
облысында. Ғана анықталған, себебі
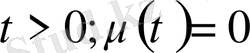 мәндерінде ғана берілген.
мәндерінде ғана берілген.
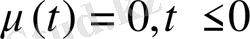 десек
десек
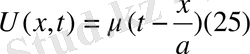 барлық облыста анықталады.
барлық облыста анықталады.
Бұл есептер шешімінен
t
x=at
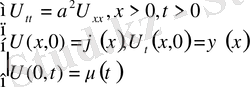 (26)
(26)
x
Есебінің шешімі құрылады.
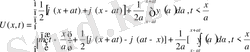
5. Кесінді есептер
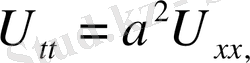
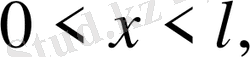
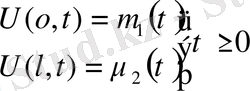 (28)
(28)
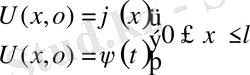
Есептің шешімі жалғастыру әдісімен құрылады
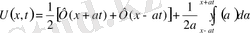
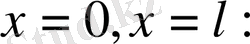
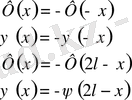
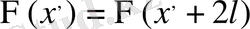
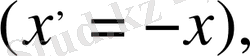
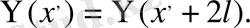
Шексіз түзу есебіндегі бастапқы шарттар қандай да бір
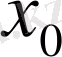 нүктесі арқылы тақ функциялар болса, онда шешім бұл нүктеде нольге айналады.
нүктесі арқылы тақ функциялар болса, онда шешім бұл нүктеде нольге айналады.
Лемма
2:
Шексіз түзу есебіндегі бастапқы шарттар қандай да бір
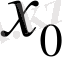 нүктесі арқылы жұп функциялар болса, онда шешімнің
нүктесі арқылы жұп функциялар болса, онда шешімнің
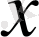 бойынша туындысы
бойынша туындысы
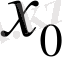 нүктесінде нольге айналады.
нүктесінде нольге айналады.
Л 1 Дәлелдеуі:
 деп аламыз.
деп аламыз.
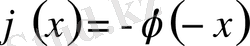 ,
,
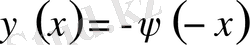 тақ болсын. Есептің шешімі
тақ болсын. Есептің шешімі
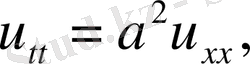
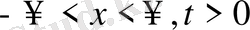
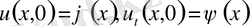
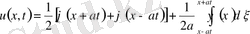
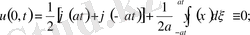
Лемма дәлелденді.
Леммалардың көмегімен келесі есептердің шешеміз
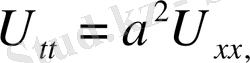
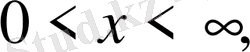
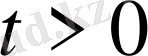 1-ші шектік есеп
1-ші шектік есеп
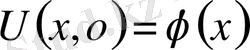
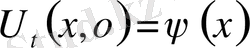
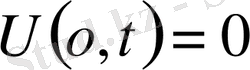
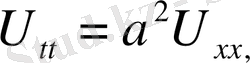
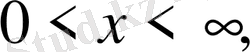
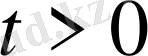 2-ші шектік есеп
2-ші шектік есеп
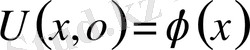
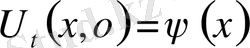
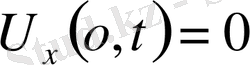
1-ші шектік есеп
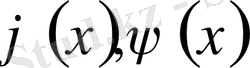
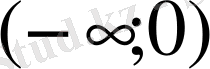
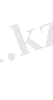
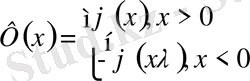
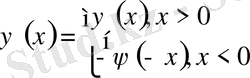
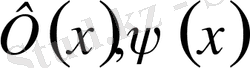
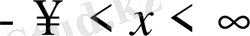
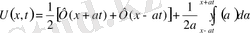
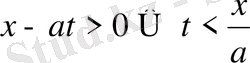
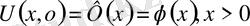
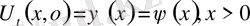
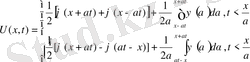
2-ші шектік есеп
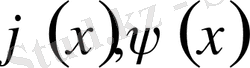
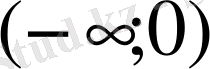
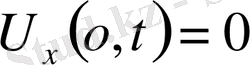
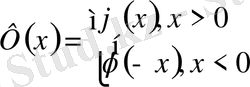
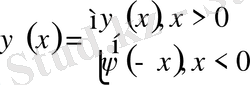
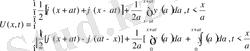
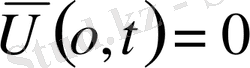 ,
,
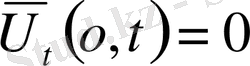
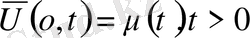
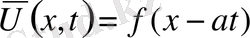
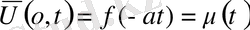
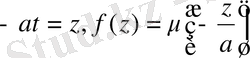
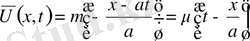
 облысында. Есептің шешімін барлық облыстар үшін табу керек.
облысында. Есептің шешімін барлық облыстар үшін табу керек.
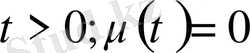
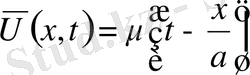
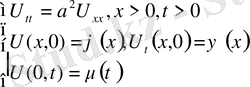
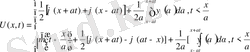
5. Кесінді есептері.
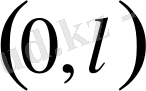 аралығында шектік есептер карастырамыз
аралығында шектік есептер карастырамыз
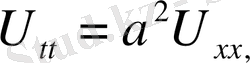
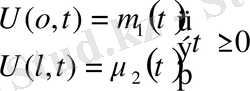
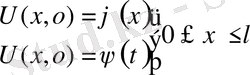
Бұл есепті шешу үшінде жалғастыру әдісі қарастырылады
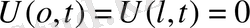
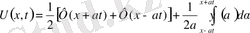
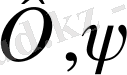 функциялары
функциялары
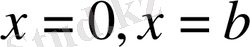 нүктелері арқылы тақ жалғастырылатын функциялар
нүктелері арқылы тақ жалғастырылатын функциялар
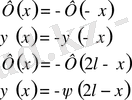
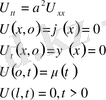
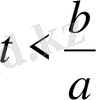
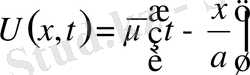
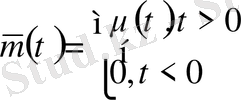
Бұл шешімнің қосындысы қатар түрінде жазылады. Усуптің шешімін береді.
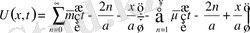
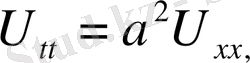
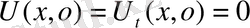
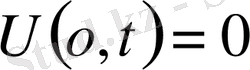
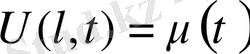
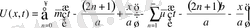
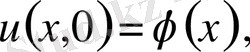
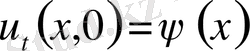 (9)
(9)
Есепті шығару үшін Даламбер формуласын қолданамыз. Ол үшін есепті келесі түрге келтіреміз.
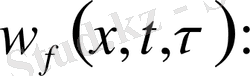
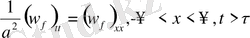 (10)
(10)
(10) теңдеудің шешімдерін қанағаттандыратын шарттар:
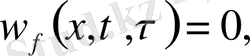
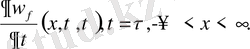 (11)
(11)
(10), (11) бұл есеп үшін Даламбер формуласы қолданылады. Онда
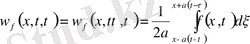 (12)
(12)
(12) формуланы пайдалана отырып, есептің шешімін мына түрде жазуға болатындығына көз жеткізейік. (9) шешімін мына түрде жазамыз.
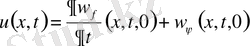 (13)
(13)
Мұндағы
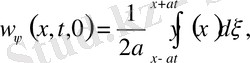
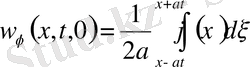
Лемма: Біртекті емес (9) теңдеудің шешімі, яғни (9) есептің шешімі бастапқы шарттарын ноль деп алғанда, яғни
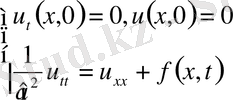 (*)
(*)
деп алғанда оның шешімі
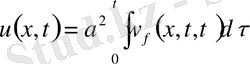 (14)
(14)
(14) шешімі екенін дәлелдеу үшін оны дифференциалдаймыз.
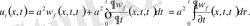
Екінші рет дифференциалдаймыз. Сонда
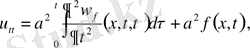
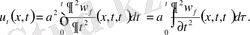
Сонымен (9) есептің шешімін жекелеген жеңіл есептердің шешімдерінің қосындысы түрінде құрамыз.
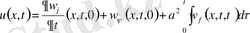 (15)
(15)
(12) формуланы пайдаланып, (15) формуладағы қосылғыштарды ашып жазамыз. Онда
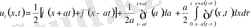 (16)
(16)
Сонымен (16) формула (9) есептің толық шешімін береді.
- Шешімнің орнықтылығы.
Шешімнің орнықтылығын зерттеу қажетті, орнықсыз шешімдер мағынасыз, қарастырылған есептердің шешімдері орнықты болу үшін бұл шешімдер қосымша шарттардан үзіліссіз тәуелді болу керек. Қандай
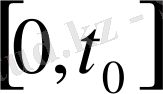 аралығында
аралығында
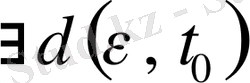 табылып,
табылып,
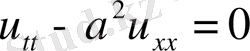 теңдеуінің екі шешімі үшін
теңдеуінің екі шешімі үшін
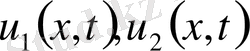 .
.
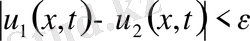 ,
,
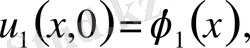
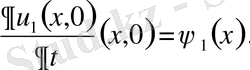
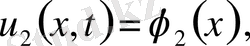
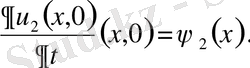
шарттары үшін тек қана
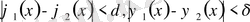
болғанда ғана орындалатын болса, шешім орнықты дейміз. Шешімнің бар және жалғыз болуы, орнықтығы мәселелерімен есептер қисынды, қисынсыз қойылған деп екі топқа бөлінеді. Есеп қисынды қойылған деп аталады, егер
- Шешімі бар болса,
- Қосымша шарттарды орындайтын жалғыз шешім болса.
- Шешім орнықты болса.
Егер бұл шарттардің әйтеуір біреуі орындалмаса есеп қисынсыз қойылған деп аталады. Практикада қисынсыз қойылған есептер де жиі кездеседі. Қисынсыз қойылған есептің мысалы:
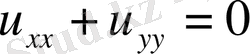 Лаплас теңдеуі
Лаплас теңдеуі
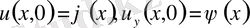 қарастырамыз. Бұл қисынсыз қойылған есеп екенін тексереміз.
қарастырамыз. Бұл қисынсыз қойылған есеп екенін тексереміз.
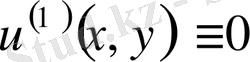 ,
,
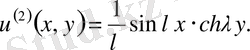
бастапқы шарттар мынадай
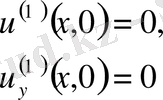
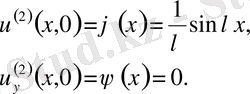
 параметрі шексіз үлкен болған кезде
параметрі шексіз үлкен болған кезде
 бастапқы шарттары мен айырмалары аз. Шешім орнықсыз, демек қисынсыз есеп.
бастапқы шарттары мен айырмалары аз. Шешім орнықсыз, демек қисынсыз есеп.
- Жарты түзу және жалғастыру әдісі.
Енді жарты түзу есептерін қарастырайық, яғни түзудің бір шеті шектеулі болған жағдайды қараймыз.
 ,
,
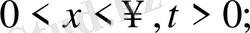
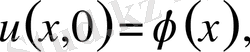
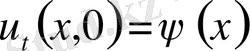 бастапқы шарттар.
бастапқы шарттар.
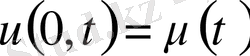 шекаралық шарттар.
шекаралық шарттар.
Бұл есепті жарты түзудің
бірінші шеттік есебі
деп атаймыз. Егер шекаралық шартта мынадай шарт қойылса
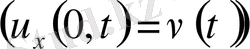 онда
екінші шеттік есебі
деп аталады.
онда
екінші шеттік есебі
деп аталады.
Бұл есептерді шешу үшін шексіз түзуде берілген есептердің шешімдерінің қасиеттерін пайдаланамыз.
Лемма
1:
Шексіз түзу есебіндегі бастапқы шарттар қандай да бір
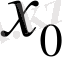 нүктесі арқылы тақ функциялар болса, онда шешім бұл нүктеде нольге айналады.
нүктесі арқылы тақ функциялар болса, онда шешім бұл нүктеде нольге айналады.
Лемма
2:
Шексіз түзу есебіндегі бастапқы шарттар қандай да бір
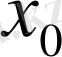 нүктесі арқылы жұп функциялар болса, онда шешімнің
нүктесі арқылы жұп функциялар болса, онда шешімнің
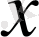 бойынша туындысы
бойынша туындысы
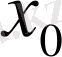 нүктесінде нольге айналады.
нүктесінде нольге айналады.
Л 1 Дәлелдеуі:
 деп аламыз.
деп аламыз.
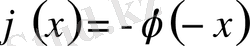 ,
,
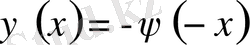 тақ болсын. Есептің шешімі
тақ болсын. Есептің шешімі
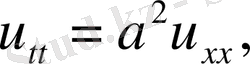
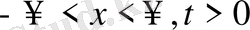
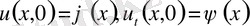
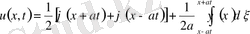
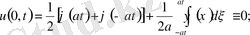
Лемма дәлелденді.
Леммалардың көмегімен келесі есептердің шешеміз
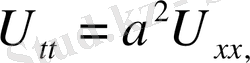
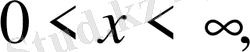
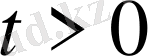 1-ші шектік есеп
1-ші шектік есеп
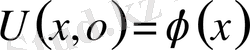
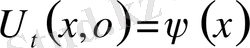
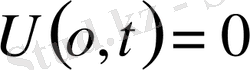
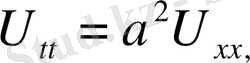
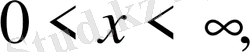
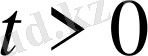 2-ші шектік есеп
2-ші шектік есеп
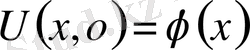
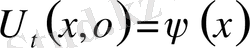
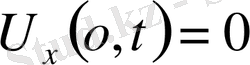
1-ші шектік есеп
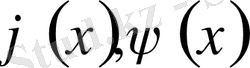
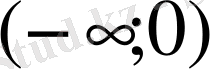
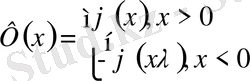
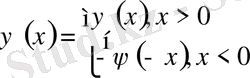
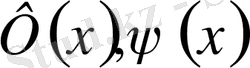
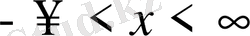
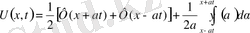
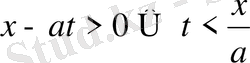
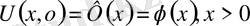
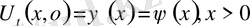
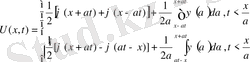
2-ші шектік есеп
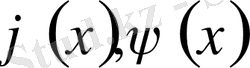
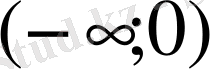
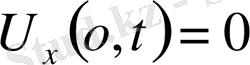
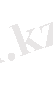
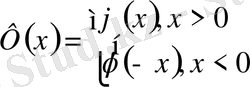
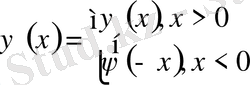
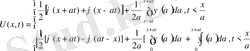
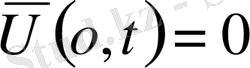 ,
,
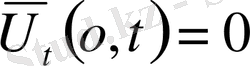
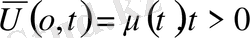
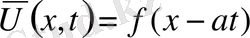
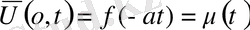
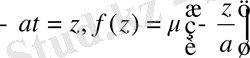
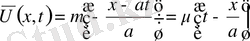
 облысында. Есептің шешімін барлық облыстар үшін табу керек.
облысында. Есептің шешімін барлық облыстар үшін табу керек.
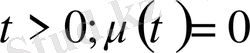
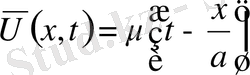
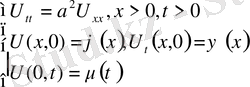
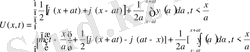
5. Кесінді есептері.
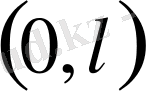 аралығында шектік есептер карастырамыз
аралығында шектік есептер карастырамыз
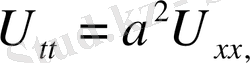
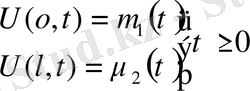
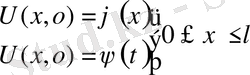
Бұл есепті шешу үшінде жалғастыру әдісі қарастырылады
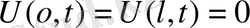
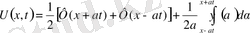
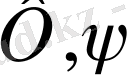 функциялары
функциялары
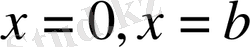 нүктелері арқылы тақ жалғастырылатын функциялар
нүктелері арқылы тақ жалғастырылатын функциялар
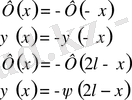
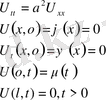
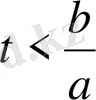
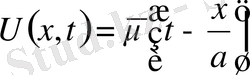
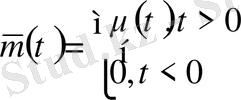
Бұл шешімнің қосындысы қатар түрінде жазылады. Усуптің шешімін береді.
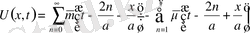
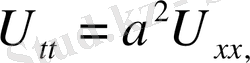
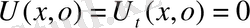
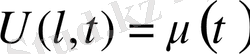
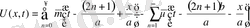 1. Шектеусіз ішек
1. Шектеусіз ішек
 Яғни х
Яғни х
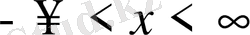 шейін өзгереді.
шейін өзгереді.
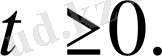
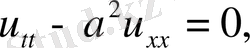
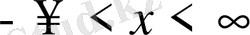 ,
,
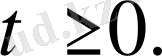 (1) (2) тырамыз. (1) теңдеудің характеристикалық теңдеуі
(1) (2) тырамыз. (1) теңдеудің характеристикалық теңдеуі
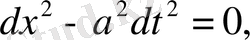
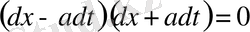
 немесе
немесе

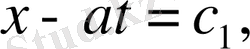
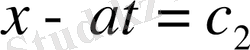
характеристикалары осылай анықталады. Енді
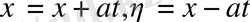 деген алмастырулар жасаймыз. Бұл алмастырулар нәтижесінде (1) теңдеу
деген алмастырулар жасаймыз. Бұл алмастырулар нәтижесінде (1) теңдеу
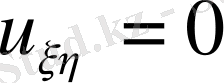 (3)
(3)
Ал бұл теңдеуді шешу оңай.
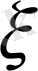 бойынша интегралдаймыз.
бойынша интегралдаймыз.
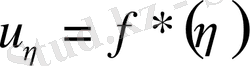
Тағы да интегралдасақ,
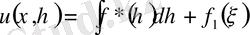
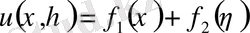 (4)
(4)
Енді
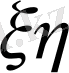 -дан қайтадан
-дан қайтадан
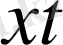 айысамыз.
айысамыз.
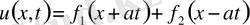 (5)
(5)
(5) (1) -дің шешімі. Онда ол (2) бастапқы шарттарды қанағаттанду керек.
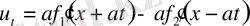
ал
 екенін ескерсек,
екенін ескерсек,
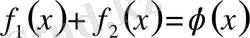
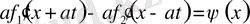
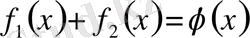
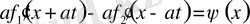
Қоссақ,
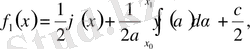
Алсақ,
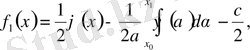
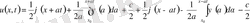
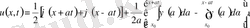
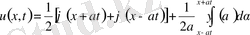 (6)
(6)
(6) - Даламбер формуласы деп аталады.
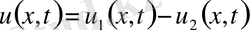 , мұндағы
, мұндағы
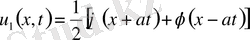 (7)
(7)
ал
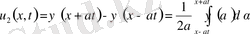 (8)
(8)
(1) -(2) есептің жалғыз шешімі (6) болады.
2. Біртекте емес теңдеулер.
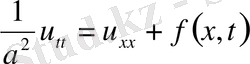 ,
,
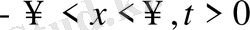 облысында қарастырамыз.
облысында қарастырамыз.
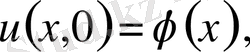
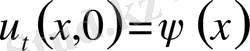 (9)
(9)
Есепті шығару үшін Даламбер формуласын қолданамыз. Ол үшін есепті келесі түрге келтіреміз.
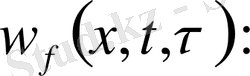
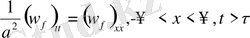 (10)
(10)
(10) теңдеудің шешімдерін қанағаттандыратын шарттар:
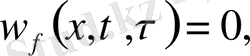
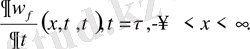 (11)
(11)
(10), (11) бұл есеп үшін Даламбер формуласы қолданылады. Онда
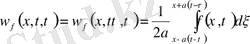 (12)
(12)
(12) формуланы пайдалана отырып, есептің шешімін мына түрде жазуға болатындығына көз жеткізейік. (9) шешімін мына түрде жазамыз.
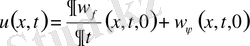 (13)
(13)
Мұндағы
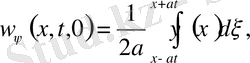
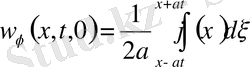
Лемма: Біртекті емес (9) теңдеудің шешімі, яғни (9) есептің шешімі бастапқы шарттарын ноль деп алғанда, яғни
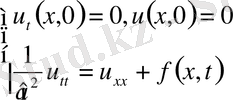 (*)
(*)
деп алғанда оның шешімі
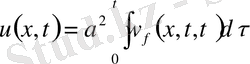 (14)
(14)
(14) шешімі екенін дәлелдеу үшін оны дифференциалдаймыз.
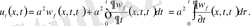
Екінші рет дифференциалдаймыз. Сонда
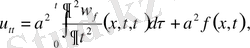
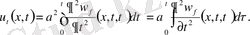
Сонымен (9) есептің шешімін жекелеген жеңіл есептердің шешімдерінің қосындысы түрінде құрамыз.
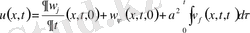 (15)
(15)
(12) формуланы пайдаланып, (15) формуладағы қосылғыштарды ашып жазамыз. Онда
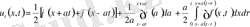 (16)
(16)
Сонымен (16) формула (9) есептің толық шешімін береді.
- Шешімнің орнықтылығы.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz