“Алгебралық сызықтық теңдеулер жүйесін шешу” тақырыптары бойынша дәрістік, зертханалық сабақтарды жүргізуде қолданылатын әдістемелік құрал жасау

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 60 бет
Таңдаулыға:

ЖОСПАР

КІРІСПЕ . . . 3

I. ТЕҢДЕУЛЕР МЕН ТЕҢДЕУЛЕР ЖҮЙЕЛЕРІНІҢ ЛОГИКАЛЫҚ ҚҰРЛЫМДАРЫН ТҮСІНДІРУ ТӘЖІРИБЕСІ 1. 1. Сызықтық теңдеулер жүйесін түсіндіру тәжірибесінен . . . 42 1. 2 Квадрат теңдеу және квадрат теңдеулер жүйесінің логикалық құрлымын түсіндіру тәжирбесінен . . . 47

ҚОРЫТЫНДЫ . . . 58

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 60

КІРІСПЕ

Орта мектепте математикалық білімдер жүйесін оқытуда теңдеулер мен теңдеулер жүйелерінің орны ерекше.

Теңдеулер мен теңдеулер жүйелерін терең түсініп меңгеру математикалық білімдерді одан әрі дамытуға, қоршаған ортадағы сан алуан құбылыстарға, терең мағыналы модельдер жасауға үйретеді.

Олай болса, теңдеулер мен теңдеулер системаларының теориялық және практикалық маңызы зор.

Дипломдық жұмыстың өзектілігі алгебралық кеңінен баяндалатын сандар жұйелері мен функциялар, теңсіздіктер сол сияқты көптеген геометриялық тұжырымдарға байланысты мәселелер, проблемалар логикалық жағынан теңдеулер мен теңдеулер жүйелері мен тығыз байланысты болады. Олай болса, теңдеулер мен теңдеулер жүйелерін аталған маңызды мәселелерден мүлде оқшау жалаң қарастыруға болмайды[1] .

Теңдеулер мен теңдеулер жүйелері орта мектеп математикасының бағдарламасының негізгі бөлімі. Бұл теңдеу мен теңдеулер системаларының орта мектеп математикасының әр түрлі саласында қолданбалы есептерді шешуге кең түрде қолданылатындығымен түсіндіріледі. Теңдеу тарихы ерте замандағы математикамен тығыз байланысты.

Мысалы, координат әдісінің және аналитикалық геометрияның пайда болуымен дамуы теңдеулерді тек алгебрада сандар жүйесінде ғана қолданып қоймай әр түрлі геометриялық фигуралар жөніндегі есепке де қолдана бастады. Бұл бағыт алгебраның дамуына өз әсерін тигізді. Теңдеу алгебралық ұғым ретінде өзінің пайда балуы жөнінен негізгі үш бөлікке бөлінеді;

теңдеу мазмұнды есептер шешу құралы;
теңдеу алгебралық объектіні үйретуге қызмет ететін ерекше формуланың ролін атқарады;
теңдеу формула ретінде қосымша санды немесе өзінің шешімі болатын нүктенің координатасын анықтайды.

Дипломдық жұмыстың мақсаты: “Алгебралық сызықтық теңдеулер жүйесін шешу” тақырыптары бойынша дәрістік, зертханалық сабақтарды жүргізуде қолданылатын әдістемелік құрал жасау.

Зерттеу жұмысының міндеттері:

Теңдеу мен теңдеулер жүйесі ұғымының шығу мен даму тарихына қысқаша тоқталу;
Алгебралық теңдеулерге есеп, сондай-ақ теңдеулер мен теңдеулер жүйелерінің арасындағы айырмашылықты айқындау;
Осы классификация бойынша жіктелген есептердің мектепте оқыту әдістемесіне тоқталу;
Оқушылар бойынан теңдеулер мен теңдеулер жүйелерін шешу әдістерін іздеу машықтарын дамыту жолдарын табу;
Алгебралық сызықтық теңдеулер мен теңдеулер жүйелерін шешу алгоритімін құрудың ең тиімді әдістері мен жолдарын анықтау.
Мысал ретінде күрделі иррационалды, парметрлі теңдеулер мен теңдеулер жүйелерін шешудің нәтижелі әдіс тәсілдерін (графикалық, ауыстыру, геометриялық, векторлық, топтастыру, т. б. ) көрсету.

Пәні: Математиканы оқыту әдістемесі.

Сонымен, теңдеу көп аспектілі жалпы математикалық ұғым. Математикалық білім беру ісінде ешбір аспектіні қалдыруға балмайды.

Теңдеу тақырыбының маңыздылығы және ауқымының кеңдігіне байланысты оны осы заманда үйретудің мазмұнды - әдістемелік бағыты - теңдеу және теңдеулер жүйесі. Бұл арада теңдеулер мен теңдеулер жүйелері ұғымын қалыптастыру үшін оларды шешудің жалпы және дербес әдістері, мектеп математикасының курсында санды, функционалдық бағыттар бойынша теңдеулер мен теңдеулер системаларын үйренудің тығыз байланыстылығы қарастырылады.

Теңдеудің пайда болу обылысы және теңдеу ұғымының алгебрадағы атқаратын міндетіне сәйкес мектеп математикасындағы теңдеулер мен теңдеулер жүйелерін үш бағытқа бөлеміз:

А) Қолданбалы бағыт. Теңдеулер мен олардың жүйелерін мазмұнды есептерді шешуге қолдану. Математиканың басқа ғылымда қолданылуын оқытудағы әдістер мен тәсілдер көбінесе теңдеулерге сүйенеді[2] .

Қазіргі математиканың басқа тарауларда қолданылуы көбінесе математикалық модельдеуге байланысты. Осы ұғымды пайдаланып теңдеулер мен олардың жүйелері математикалық модельдеудегі негізгі құрал ретінде аңықталады.

Б) Теңдеу мен теңдеулер жүйелерін үйренудегі теориялық - математикалық бағыт екі аспектіден тұрады:

1. аса маңызды теңдеулер және олардың жүйелерінің класын оқу,

2. бір бағытқа жататын жалпыланған ұғымдармен әдістерді бүтіндей үйрену. Осы екі аспекті де мектеп математикасында аса қажет.

Теңдеулердің негізгі кластары жай және әрі аса маңызды математикалық модельдермен тығыз байланысты.

Зерттеу объектісі: Математикалық сызықтық теңдеулер мен теңдеулер жүйелері ұғымы.

Дипломдық жұмыс кіріспеден және 3 тараудан тұрады. Кіріспеде тақырыптың өзектілігі, мақсаты мен міндеті, пәні, зерттеу обьектісі қарастырылған.

1. Мектепте теңдеулер мен теңдеулер жүйелерін оқытудың әдістемесі 1. 1. Сызықтық теңдеулер мен теңдеулер жүйелерінің ғылыми теориялық мазмұны

Мектепте математикалық білім беру жүйесінде теңдеулер мен теңдеулер жүйелерінің маңызы үлкен. Олар теориялық білімдер мазмұны мен бірге танымдық практикалық тұрмысынан қарағанда оқушылардың математикалық ойлау жүйесінің дамуына айтарлықтай ықпал жасайды.

Теңдеңдеулер мен теңдеулер жүйелері оқушыларды қоршаған ортадағы саналуан объектілер арасындағы байланыстарды ашуға, оларды танып білуге, осндай объектілердің байланыстарына математикалық модель жасауға үйретеді. Логикалық жағынан дұрыс және айқын жасалған модельдер есептерді тиімді шешуге, оларды практикалық өмірімізде қолдануға жағдайды.

Жан-жақты терең жасалған талдаулар оқушылардың материалдық толық түсінуіне мүмкіндік тудырады.

Жеке теңдеулердің шешімдері бір сандар құрамында немесе бірнеше сандар құрамында болмау мүмкін. Олардың шешімдері сандардың кеңейтілген құрамында болуы мүмкін. Олай болса, теңдеңдеулер мен теңдеулер жүйелерін шешу барысында сандар құрамдарымен тығыз байланыста қарастырған жөн.

Теңдеңдеулер мен теңдеулер жүйелерін шешу барысында шешудің жалпы тәсілін таңдай білудің үлкен танымдық маңызы бар[3] .

Теңдеңдеулер мен теңдеулер жүйелерін ұтымды тәсілдер арқылы шешу оқушыларды іскерлікке, тапқырлыққа, өздігінен дұрыс қорытынды жасай білуге үйретеді.

Оқушылардың жалпы математикалық білім деңгейлерінің дамуына, қалыптасуына мүмкін болатын жағдайда теңдеңдеулер мен теңдеулер жүйелерін графиктік жолмен шешудің де айтарлықтай пайдасы бар. Олай болса, теңдеңдеулер мен теңдеулер жүйелерін функция ұғымы мен логикалық сәйкестікті қарсатырған, зерттеген жөн.

Мысалы, ax^2+bx+c=0 квадрат теңдеуін графиктік жолмен шешу үшін берілген теңдеуге логикалық жағынан сәйкес келетін y=ax^2+bx+c квадраттық функциясының гафигін саламыз. Егер берілген квадрат теңдеудің нақты түбірлері болса, онда олар сәйкес параболаның абциссалар осімен қиылысу нүктелері болады.

Мектепте, теңдеулер мен теңдеулер жүйелін оқыту программалық жүйесін басшылыққа ала отырып, оларды сәйкес логикалық даму тұрғысынан қарастыруды дұрыс санаймыз. Осы мақсатпен алдымен жай бір белгісізді сызықтық теңдеулерден бастап, біртіндеп оқушылардың математикалық түсініктерінің дамуына лайықтап теңдеулер мен теңдеулер жүйелерін күрделілендіруге көшуді әдістемелік талапқа сай келеді деп есептейміз.

Егер белгісіз шамаға саны шектелген қосу, көбейту, бөлу, бүтін дәрәжеге дәрежелеу және түбір табу операциялары орындалса, онда теңдеуді алгебралық теңдеу деп атайды.

түріндегі теңдеуді бір белгісізі бар алгебрадық

теңдеу деп атайды. Мұндағы n - бүтін және теріс емес сан, теңдеудің кофиценттері; x - белгісіз, сондықтан ізделінетін айнымалымыз болып табылады, n - нешеге тең болса, сол теңдеудің дәрежесі болып табылады. Мысалы, 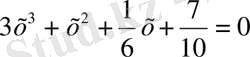. Бұл теңдеудің дәрежесі 3 - ке тең, дәрежесі 2 - ке тең, сондықтан бұл теңдеу 2 -ші дәрежелі квадрат теңдеу. (1) - ші теңдеуді қанағаттандыратын, яғни (1) - теңдеуді нөлге айналдыратын белгісіз х- тің мәнін, (1) - теңдеудің шешімдері деп атаймыз. Мысалы, х ² -4х+3=0 теңдеуінің шешімдері бар. Олар: x ₁ =1 ; x ₂ =3.

Оқушылар теңдеулерді төменгі кластан бастап - ақ шешіп келеді. Алайда теңдеудегі әріп оларға айнымалы деп таныстырылмай, белгісіз сан ретінде қарастырылып келеді. Сондықтан теңдеудің түбірі ұғымын қалыптастыру негізінен 4 кластан басталады. Енді әріптің орнына айнымалының кез - келген мәнін қоюғаболады. Кейбір жағдайларда дәл теңдіктер, екінші жағдайларда дәл емес теңдіктер шығады. Айнымалылардың орындарына қойғанда дәл теңдік шығатын мәндерін теңдеудің түбірлері деп атаймыз.

Мына есепті шешейік: “Екі сөреде 40 кітап тұр, сонда үстіңгі сөредегі кітап төмендегіден 3 есе көп. Төменгі сөреде неше кітап бар?” . Төменгі сөредегі кітап санын х әрпімен белгілейік. Сонда үстіңгі сөредегі кітап саны 3х-ке тең. Есептің шарты бойынша сөреде 40 кітап бар. Осы шартты төмендегі теңдеу түрінде жазуға болады.

3х+х=40

Кітаптың белгісіз санын табу үшін, біз айнымалысы бар өрнек құрдық. 3x+x=40 теңдеуіндігі х - тіңорнына қойғанда дәл теңдік шығатын санды табу керек. Мұндай санды теңдеудің шешімі немесе түбірі деп атайды.

3х+х=40 теңдеудің бір шешімі бар, себебі n=1.

Екі, үш және одан да көп түбірлері болатын немесе жалпы алғанда түбірлері болмайтын теңдеулерді мысалға келтіруге болады[4] .

Мысалы, (x-4) *(x-5) *(x-6) =0 теңдеуінің үш шешімі бар, олар : 4; 5; 6. Шындығында, осы сандардың әрқайсысы (х-4) *(x-5) *(x-6) көбейтіндісінің бір көбейткіш нөлге айналдырады, олай болса, көбейтіндінің өзін де нөлге айналдырады. х-тің басқа кез-келген мәнінде көбейткішті нөлге айналдырады. Олай боса көбейтіндінің өзін де нөге айнадырадбы х-тің басқа кез - келген мэнінде көбейткіштердің бірде - біреуі нөлге айналмайды. Олай болса көбейтінді де нөге айналмайды.

Х+2=х тендеуінің шешімі болмайды, өйткені х- тің тиянақты мәнінде теңдеудің сол бөлігі оң бөлігінен 2-ге артық болады. Демек, теңдеуді шешу дегеніміз - оның барлық түбірлерінің табу немесе түбірлерінің жоқ екендігін дәлелдеу деген сөз.

3х-7=14 және 2х+1=15 теңдеулерінің шешуін қарастырып, онда бұл екі теңдеудің де шешімі бірдей x=7 болатынын білеміз.

Егер екі теңдеудің шешімі бірдей болса, онда ол теңдеулер мәндес теңдеулер деп аталады.

X+3=x+5 және 3x+7=3x теңдеулерінің түбірлері жоқ, себебі х - ке қандай мән берсек те, бұл теңдеулердің сол жағы мен оң жағының мәндері тең болмайды. Сонымен, бұл екі теңдеудің брде-бір шешімі болмайды. Түбірі жоқ теңдеулерде мәндес теңдеулер болып табылады.

2x+5=3x+5-x және 3x=3x-4+4 немесе 2x+5=2x+5 және 3x=3x теңдеулерінде теңдіктің екі жағында да бірдей өрнектер тұр. Сондықтан х -тің мәні қандай болғанда да бұл теңдеулердің оң жақтары мен сол жақтары бірдей санға тең болатын түсінікті. Аңықтама бойынша бұл теңдеулер де мәндес теңдеулер, өйткені бұрардың әрқайсысының барлық түбірлері қалғандарының да шешімі болады.

Көп жағдайда берілген алгебралық теңдеу күрделі формада өрнектелуі мүмкін. Сондықтан, берілген теңдеуді шшуге қойылатын негізгі мақсаттардың біріне саналады. Мұндай мақсатты жүзеге асыру үшін, берілген теңдеудің құрлымдық мағынасын сақтай отырып, қажетті түрлендірулерді жүзеге асырамыз. Ал бұл проблеманы жүзеге асыру үшін теңдеуге лайықты, оның қасиеттері деп аталатын арнайы тұжырымдардың мағыналарына жан - жақты талдау жасау керек.

Теңдеудің қасиеттері :

1. Егер теңдеудің екі бөлігіне де бірдей санды ( шаманы ) қосса, онда берілген теңдеумен мәндес теңдеу шығады.

Төмендегі теңдеу берілген болсын дейік.

4х+5=33. Мұны шешіп, бір ғана х = 7 түбірін табамыз. Теңдеудің екі бөлігіне де -5; 2, 4; -12 сандарын қосып, төмендегі теңдеулерді шығарып аламыз.

4х+5+(-5) = 33+(-5), 4x = 28,

4x+5+2, 4 = 33+2, 4, немесе 4x+7, 4 = 35, 4

4x+5+(-12) =33+(-12) 4x-7 =21

Бұларды шешіп, барлық теңдеулердің түбірі 7-ке тең екенін табамыз. Қортынды. Теңдеудің екі жағына бірдей шаманы қосқаннан теңдеудің мәні өзгермейді.

Егер теңдеудің екі бөлігін де бірдей шамаға кемітсек, онда берілген теңдеумен мәндес теңдеу шығады.

2х+5 = 15 теңдеуін қарастырайық. Теңдеу шешіп, бір ғана х=5 түбірін табамыз. Теңдеудің екі жағын да 3 санына кемітсек төмендегі теңдеу шығады.

2х+5-3=15

2х+2=12 х=5.

Бұл теңдеуді де шешсек, түбірі 5 санына тең болатын көреміз. Бұдан шығатын қортынды: теңдеудің екі жағын бірдей шамаға кеміткеннен теңдеудің мәні өзгермейді.

Егер теңдеудің екі жағын да нөлге тең емес бір санға ( шамаға ) көбейтсек, одан шыққан жаңа теңдеу берілген теңдеумен мәндес болады.

4х-7=13 теңдеуін қарастырайық.

Бұл теңдеудің бір ғана х=5 түбірі бар. Теңдеудің екі жағын да 2-ге: 5 - ке: ¼ - ге көбейтіп, төмендегі теңдеулерді шығарып аламыз:

-8х+14= - 26; 20х - 35 = 65; х -7/4= 13/4. Бұл теңдеулерді шешсек, бәрінің де түбірі х= 5 болып шығады. Демек, бұл берілген теңдеумен мәндес. Теңдеудің бұл қасиетінен шығатын қортынды: теңдеудің екі жағын да бірдей шамаға көбейткеннен, теңдеудің мәні өзгермейді[5] .

4. Егер теңдеудің екі жэағын да нөлге тең емес бір санға ( шамаға ) бөлсек, одан шыққан жаңа теңдеу берілген теңдеуменмәндес болады.

3х+2=8 теңдеуін қарастырайық.

Бұл теңдеудің бір ғана х =2 деген түбірі бар. Теңдеудің екі жағын да 4 санына бөлсек, 3/4х+1/2 =2 теңдеуі шығады. Бұл теңдеудің де бір ғана х =2 деген түбірі екеніне оңай көз жеткізуге болады.

Қортынды: теңдеудің екі жағын да бірдей санға бөлгеннен теңдеудің өзгермейді.

5. Егер теңдеудегі қосылғыштардың бірін теңдеудің екінші жағынан қарама - қарсы таңбамен көшірсек, онда берілген теңдеумен мәндес теңдеу шығады. Мысалы, 5х =2х+9 теңдеуінің оң жағындағы 2х қосылғышын теңдеудің сол жағына қарама - қарсы таңбамен көшіріп, сол теңдеумен мәндес 5х - 2х =9 теңдеуін шығарып аламыз.

Теңдеудің бұл қасиетінін шығатын қортынды: теңдеудің бір жағындағы мүмкін теңдеудің екінші жағына қарама - қарсы таңбамен көшіруге болады.

Теңдеулер мен теңдеулер жүйелерінің қатаң логикалық байланыстарын дұрыс тапып білу арқылы оқушы өзінің жолдастарының арасында, ата - ананың алдында, іні - қарындастароы мен аға - апаларының алдында сол сияқты танымайтын адамдар арасында өзін қалай ұстай білуді іштей терең сезінетін болады. Өйткені, логикалық жағынан дәл және терең, ішкі және сыртқы байланыстар тәртіпсіздіктермен, көргенсіздіктермен, өнегесіздіктермен, бұзақылықтармен мүлде сиыспайды.

Математикалық логикалық байланыстар мағынасыздықтар, бұрмалаушылықтарға, берекесіздіктерге, негізсіз пікірлерге, дәлелсіз болжамдарға төзе алмайды.

Математика өзінің ішкі логикалық тазалығы жан - жақты және толық сақталғанда ғана сан - алуан толып жатқан құбылыстародың ішкі сырын танып білетін ең құдіреті күшке айналады. Оған байланысты, практикалық маңызы үлкен тәрбие мәселеріне қолданалық таза логикалық өнегені керегімізге пайдалана аламыз.

Теңдеулер мен теңдеулер жүйелері жөнінде оқушылардың білімдері дәйекті және баяндыболу үшін, жаңа тақырыптарды түсіндіру кезінде, практикалық маңызы үлкен мәселелерді қарастыруда, оқушылар жаңа білім бұлағына толық зейін қойып, үлкен ықыласпен, ынталы іс - қимылдар тапыта білу керек. Аталған мәселелерді саналы түрде меңгеріп, олардың практикалық қолданымдарын терең сезінгенде ғана қушының математикалық білімі сапады болады.

Теңдеулер мен теңдеулер жүйелерін меңгеріп қана қоймай, оны ұзақ уақыт есте сақтап, өзінің практикалық қажеттеріне пайдалану мүмкіндігіне ие болу үшін оқушылар теориялық мәселелерді әр түрлі оқу құралдарын пайдалану ақылы бірнеше рет қайталауы, шарттары сан - алуан көптеген жаттығуларды мол шешу керек[6] .

1. 2 Сызықтық теңдеулер жүйесін матрицалар арқылы анықтау

mхn нақты сандарды немесе басқа бiр элементтердi m жатық жолға n тiк жолға орналастырған тiкбұрышты таблицаны мөлшерi болатын матрица деп атаймыз.

Матрицаның элементтерiн деп белгiлесек, i - индексi жатық жолдың нөмерiн, ал j - индексi тiк жолдың номерiн көрсетедi. Матрицаны былай белгiлеймiз:

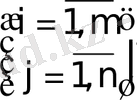
Мысал.

. Егер m=n болса, онда матрицаны n-реттi квадрат матрица деп атайды. Егер A _mxn , B _mxn екi матрицаның сәйкес элементтерi a _ij =b _ij болса, онда олар бiр-бiрiне тең болады, яғни A _mxn =B _mxn.

1xn мөлшерлi матрицаны А _1xn =(a ₁ , a ₂ , . . . , a _n ) жатық жолды матрица , ал mx1 мөлшерлi матрицаны бағана матрица деймiз. Квадрат матрицаның a ₁₁ , a ₂₂ , . . . , a _nn элементтерi оның бас диагоналын , ал a _1n , a _2n-1 , . . . , a _n1 - қосалқы диагоналын қґрайды. Егер a _ij =0 болса, онда матрицаны нөлдiк матрица деймiз, егер квадрат матрицаның бас диагоналының бойындағы элементтерiнен басқа элементтер нөл болса, онда матрицаны диагональ матрица дейдi.

Егер диагональ матрицада a _ij =1 (i=j) болса, онда оны бiрлiк матрица деймiз:

;

Егер квадрат матрицаның жатық жолдары мен тiк жолдарының орындарын ауыстырсақ, онда матрицаны транспонирланғен матрица деп атаймыз . Оны былай белгiлейдi А ^т .

Егер квадрат матрицаның бас немесе қосалқы диагоналдарының астындағы (немесе үстiндегi) барлық элементтерi нөлге тең болса, оны үшбұрышты матрица деймiз[7] . Егер квадрат матрицада а _ij =a _ji болса, онда оны симметриялы деймiз.

Мысал.

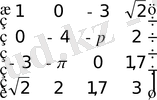Мына түрдегi матрицаны:

мұндағы a ₁₁ , a ₂₂ , . . . , a _кк 0, трапеция формалы матрица деймiз . Егер квадрат матрицаның анықтауышы болса, онда ол ерекше емес матрица делiнедi де, ал болғанда, ол ерекше матрица делiнедi. -ны кейiн қарастырамыз.

-A - керi таңбалы матрица, оның элементтерi- a _ij -ға тең болады.

Матрицаға сызықтық амалдар қолданайық.

Кез келген матрицаны бiр санға көбейтуге болады, яғни, мұнда. Сонымен матрицаны бiр санға көбейту үшiн, оның барлық элементтерiн осы санға көбейтемiз.
болса, онда, мұндағыяғни матрицалардың сәйкес элементтерiн қосамыз.

Мысалдар.

Матрицалардың сызықтық амалдарының қасиеттерi:

А+В=B+A
(A+B) +C=A+(B+C)
A+0=A
A+(-A) =0, -A-керi таңбалы матрица

Бұл қасиеттер сызықтық амалдардың анықтамасы арқылы дәлелденедi.

Екi матрицаны өзара көбейтудiң ерекше ережесi бар[8] .

А _mxn =(a _ij ) матрицасының B _nxp =(b _ij ) матрицасына көбейтiндiсi деп С _mxp =(c _ij ) матрицасын айтамыз. Мұнда

Мысал.

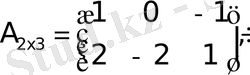
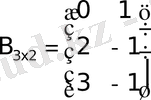
Матрицаларды көбейту үшiн мына ережелердi есте ұстау керек.

Көбейткiш матрицалар реттелген болуы керек, яғни бiр көбейткiштi бiрiншi, басқасын екiншi көбейткiш деп алуымыз керек.
Бiрiншi матрицаның тiк жолдар (бағаналар) саны екiншi матрицаның жатық жолдар саны тең болуы керек.
Көбейтудiң нәтижесiнде жатық жолдар саны бiрiншi матрицаның жатық жолдар санына тең, ал бағаналар саны - екiншi матрицаның бағаналар санына тең матрица шығады, яғни Amxnболса, екiншi көбейткiш Bnxpболса, онда көбейтiндi Сmxpмөлшерлi болады.

Мысалы. A _2x3 , B _3x4 болса, онда A _2x3 * B _3x4 =С _2х4 шығады, B _3x4 , A _2x3 -ке көбейтуге болмайды.

Матрицаны матрицаға көбейту амалының қасиеттерi:

A(BC) =(AB) C
A(B+C) =AB+AC
A(B) =(A) B=(AB)
(AB) T=BTAT

Матрицаларды көбейтудiң сандарды көбейтуден басқа ерекшелiктерi бар.

болуы мүмкiн

;

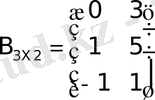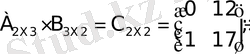
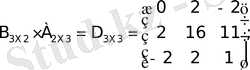
алболуы мүмкiн

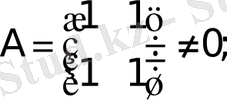
ал .

Мысалдар:

Егер,, болғанда,

D=(C-A) B табу керек.

Шешеуi:

; .

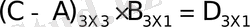Егерболса жәнеболса, табу керек.

Шешуi:

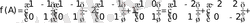
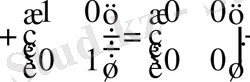
Анықтауыштар:

Әрбiр квадраттық матрицаға оның анықтауышы деп аталатын сан сәйкес келеді. Матрицаның анықтауышы осы матрицаның элементтерi арқылы берiлген бiр тәртiппен есептелiнiп табылады. Анықтауышты былай белгiлеймiз:

Екiншi реттi анықтауыш (онда екi жатық, екi тiк жол болады) былай есептелiнедi:

Үшiншi реттi анықтауыш

1 - сурет 3 - ші ретті квадрат матрицаның Саррюс ережесi

Үшiншi реттi анықтауышты есептеп шығару үшiн Саррюс ережесi қолданылады: “+” таңбамен бас диагональдағы элементтердiң көбейтiндiсi және оған екi параллель орналасқан элементтердiң қарама-қарсы бұрыштағы элементпен көбейтiндiсi алынады:

“-” таңбамен қосалқы диагональ бойындағы элементтердiң көбейтiндiсi және осы диагональға паралель орналасқан элементтердiң қарама-қарсы орналасқан элементтермен көбейтiндiсi алынады[7] :.

Мысал:

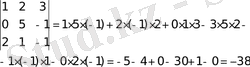
Алмастырудың түсiнiгiн қарастырайық. n натурал сандарын 1, 2, 3, . . . , n алып, оларды берiлген бiр тәртiппен бiр-бiрлеп жазып жатық жол құрсақ, оны алмастыру деймiз .

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.