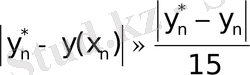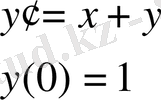Рунге-Кутта әдісі негізінде бірінші реттік дифференциалдық теңдеулерді сандық шешудің Turbo Pascal бағдарламасын әзірлеу


«Түркістан Қ. А. Ясауи» кәсіби колледжі
Курстық жұмыс
Тақырыбы: Рунге-Кутта әдісі бойынша теңдеуді шешу бағдарламасын құру.
Орындаған: Баймбетова Б.
Тобы: ТБ-1108
Қабылдаған: Баялы А. Т
Түркістан-2008 ж.
Мазмұны
Кіріспе
I бөлім. Дифференциалдық теңдеулерді сандық шешу жуықтау әдісі . . .
- Жуықтап шешу әдістері . . .
- Эйлер әдісі . . .
II бөлім. Коши есебін Рунге кутта әдісімен қарастыру . . .
2. 1 Рунге Кутта әдісі . . .
2. 2 Теңдеуді Эйлер жәнен Рунге Кутта әдістеріне мысалдар бойынша модельдеу . . .
Қосымша
Қорытынды
Пайдаланылған әдебиеттер тізімі
Кіріспе
Бағдарламалаушы жұмыс істеу үшін оған керекті бағдарламаларды бағдарламалаушы адам жасайды. Бағдарламалаушы мамандығы дүние жүзіндегі ең бір тапшы мамандықтардың бірі. Оқып шығып бірден бағдарламалаушы бола салатын ешқандай оқу құралы жоқ.
Бұл курстық жобада программалау қосымшасының жұмыс процесі кезінде қандай оқиғалар өтетіндігін анықтау, осы оқиғалар үшін процедуралар бағдарламасын жасау.
Ғылымға, экономикаға, өндіріске ақпараттық процестерді енгізу ісін жоғары қарқынмен жүргізу үшін қазіргі ақпараттық технологияларға негізделген білім жүйесінің жаңа модельін құру қажет. Адамның өз шығармашылық потенциялын толық аша алатындай, өз мүмкіндіктерін дамытып, өз білімін үздіксіз шыңдай алатындай жағдай жасалғаны абзал.
Бұл курстық жобада f(x) =0 сызықтық емес теңдеулер түбірін іздеу тапсырмалары көрсетілген. Сызықтық емес теңдеулер есептерін шешуде неше түрлі әдістер қолданылады. Теңдеулердің мұндай есептеулерін іздеу инженерлік және ғылыми есептерде көп пайдалы.
Функциялардың аналитикалық ережелеріне талдау жасауға қиын болған кезде сандық әдістерді пайдаланған тиімді.
Курстық жобада біз сызықтық емес теңдеулер түріне бағдарлама құрдық. Бұл Эйлер әдісі бойынша жақындату әдісімен жүзеге асырылады. Бағдарлама берілген интервалда барлық теңдеулер түбірін есептейді. Бағдарлама құру барысында пайдаланушының әр түрлі әдістермен есептеу жүргізуіне подпрограммалар пайдаланылған.
Курстық жобаның мақсаты: Турбо Паскаль бағдарламасында бірнеше математикалық есептерді зерттеу. Көп ағымдылық барысында туындайтын қайшылықтарды тауып, оларды шешу жолдарын анықтау.
Зерттеу міндеттері: Турбо Паскаль бағдарламасында кез-келген ағымды есептердің нәтижесін мәндерін талдау. Көп ағымды есептердің программасының серверін қолданылу жолдарын қарастыру. Есептің еркін моделін, баяндалуын, іс жүзінде көрсету.
Зерттеу пәні: Өндірістік және экономикалық процестерді модельдеу.
Зерттеу әдістері: Техникалық журналдар, ғылыми әдістемелік оқулықтар, интернеттегі бағдарламалық сайттар, схемалар.
Курстық жобаның құрылымы: Кіріспеден, екі бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады.
Курстық жобаның көрнекілігі: компьютер, проектор. схемалар.
1. Бөлім. Дифференциалдық теңдеулерді сандық шешу
жуықтау әдісі
Қарапайым дифференциалдық теңдеу болып бірінші ретті дифференционалдық теңдеу табылады
Equation. 3 (1)
Коши есебі.
Equation. 3 (2)
бастапқы шартын қанағаттандыратын (1) теңдеуінін
 Equation. 3 түбірін табу керек, басқаша айтқанда, берілген
Equation. 3 түбірін табу керек, басқаша айтқанда, берілген
 Equation. 3 нүктеден өтетін
Equation. 3 нүктеден өтетін
 Equation. 3 интегралдық қисығын табу керек
Equation. 3 интегралдық қисығын табу керек
у
у=у(х)
у
у 0 М 0
0 х 0 х
Егер
 Equation. 3 функциясы
Equation. 3 функциясы
 Equation. 3 теңсіздік-терімен анықталған
R
облысында үзіліссіз болса, онда
Equation. 3 теңсіздік-терімен анықталған
R
облысында үзіліссіз болса, онда
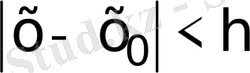 Equation. 3 (h-оң сан) маңайында кемінде бір
Equation. 3 (h-оң сан) маңайында кемінде бір
 Equation. 3 шешімі бар.
Equation. 3 шешімі бар.
Егер R облысында Липшиц шарты орындалса
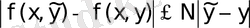 Equation. 3,
Equation. 3,
онда бұл шешімі жалғыз болады, мұндағы N -тұрақты (Липшиц константасы), жалпы жағдайда a және в дан тәуелді.
Егер
 функциясының
R
облысында шенелген
функциясының
R
облысында шенелген
 туындысы бар болса, онда
N
ретінде
туындысы бар болса, онда
N
ретінде
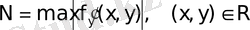
алуға болады.
1. 1. Жуықтап шешу әдісітері
Коши есебін қарастырайық. Біртіндеп жуықтау әдісі бойынша
 шешімі
шешімі
 функциясынын тізбектерінін шегі ретінде қарастырылады. Жоғарыда айтылған шарттар қанағаттандырылсын деп ұйғарсақ, келесі рекуренттік формула бойынша
функциясынын тізбектерінін шегі ретінде қарастырылады. Жоғарыда айтылған шарттар қанағаттандырылсын деп ұйғарсақ, келесі рекуренттік формула бойынша
 табылады
табылады
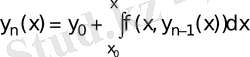 Equation. 3 (3)
Equation. 3 (3)
1. 2. ЭЙЛЕР ӘДІСІ
Коши есебін карастырайык. Эйлер әдісінің негізгі формуласы
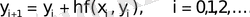
мұндағы h-қадам,
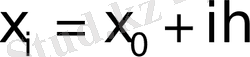 .
.
Эйлер әдісінің бағалау қателігі

мұндағы
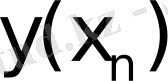 -теңдеудін шешімінің дәл мәні (болғанда),
-теңдеудін шешімінің дәл мәні (болғанда),
 -ші қадамдағы алынған жуық мән.
-ші қадамдағы алынған жуық мән.
2. Бөлім. Коши есебін Рунге кутта әдісімен қарастыру
2. 1. Рунге Кутта әдісі
Коши есебін қарастырайық.
 Equation. 3 арқылы ізделінді шешімнін
Equation. 3 арқылы ізделінді шешімнін
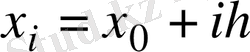 Equation. 3 нүктесіндегі жуык мәнін белгілейік. Рунге-Кутт әдісі бойынша ізделінді функцяның мәндер тізбегін есептеу формуласы
Equation. 3 нүктесіндегі жуык мәнін белгілейік. Рунге-Кутт әдісі бойынша ізделінді функцяның мәндер тізбегін есептеу формуласы

мұндағы
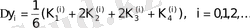

Бағалау қателігі
мұндағы
 -
-
 нүктесіндегі берілген теңдеудін шешімінін дәл мәні,
нүктесіндегі берілген теңдеудін шешімінін дәл мәні,
- мәндері h/2 және h қадаммен алынған жуық мәндер.
2. 2. Теңдеуді Эйлер жәнен Рунге Кутта әдістеріне мысалдар бойынша модельдеу
1-мысал
Коши есебінің [0; 0, 2] кесіндіде ε=10 -5 дәлдігімен жуық шешімін табу керек
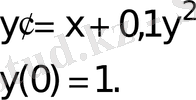
Шешуі. Бастапқы жуықтауды келесі түрде аламыз
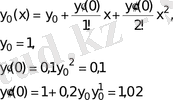 Equation. 3
Equation. 3
осыдан
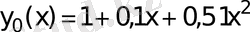 Equation. 3 . (3) -ші формуланы қолдансақ
Equation. 3 . (3) -ші формуланы қолдансақ
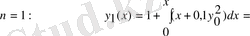
(4)
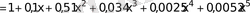 Equation. 3 .
Equation. 3 .
Келесі айырым x =0, 2 болғанда ε мәнінен үлкен болады
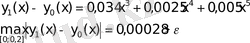
(4) өрнектегі соңғы екі қосындылардын косындысы ε шамасынан кіші, сондықтан
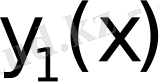 Equation. 3 келесі түрде алуға болады
Equation. 3 келесі түрде алуға болады

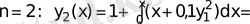
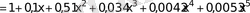
Келесі айырым [0; 0, 2] кесіндісінде ε мәнінен кіші
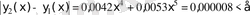
Жауабы:
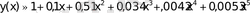
2-мысал
Коши есебімен
анықталған, қадамы
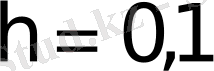 болғанда у функциясының төрт мәнін Эйлер әдісін қолдана отырып табу керек.
болғанда у функциясының төрт мәнін Эйлер әдісін қолдана отырып табу керек.
Шешуі.
Бастапқы шарттан
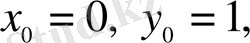 сондықтан аргумент мәндері
сондықтан аргумент мәндері
у функциясының мәндері
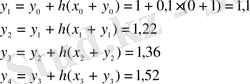
Жауабы:
3-мысал
Бірінші ретті дифференциалдық теңдеудің шешімін Рунге-Кутт әдісімен табу керек
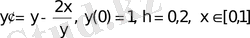
Шешуі.
Есептің шарты бойынша

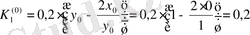
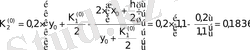
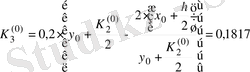

Осыдан

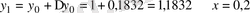 болғанда
болғанда
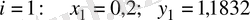 .
.
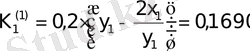
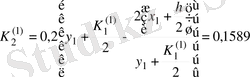
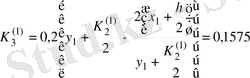
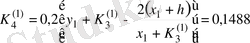

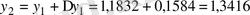
Осы сияқты
 мәндеріне сәйкес
мәндеріне сәйкес
 функция мәндерін табамыз.
функция мәндерін табамыз.
Қосымша
блок схема:
Ввод a, b, y0, m
x = a; h = (b - a) /m;
y1 = y; y2 = y; y3 = y;
c(1) = 0; c(2) = 0, 5;
c(3) = 0, 5; c(4) = 1.
Вывод x, y1, y2, y3
i = 1, m End
y1 = y1 + hf(x, y1)
j = 1, 2
k0(j) = hf(x + 2c(j) h, y2 + 2c(j) k0(j - 1) )
y2 = y2 + (k0(1) + k0(2) ) /2
j = 1, 4
k(j) = hf(x + c(j) h, y2 + c(j) k(j - 1) )
y3 = y3 + (k(1) + 2k(2) + 2k(3) + k(4) ) /6
x = x + h
Вывод x, y1, y2, y3
Қарапайым дифференциалдық теңдеулерді сандық шешудің Эйлер әдісін
Pascal тілінде құру бағдарлама
program ;
uses Crt;
const c:array[1. . 4] of real =(0, 0. 5, 0. 5, 1) ;
type
coef= array[0. . 4] of real;
var
i, j, m:integer;
a, b, h, x, y, y1, y2, y3:real;
k0, k:coef;
ch:char;
function f(x, y:real) :real;
BEGIN
f := x + у
END;
procedure Pausa;
BEGIN
WRITELN; WRITELN ('Для продолжения нажмите любую клавишу . . . ') ;
REPEAT ch := readkey UNTIL ch <> '';
END;
ВЕGIN
ClrScr;
WRITELN ('Введите значения концов отрезка [a, b] ') ;
READ (a, b) ;
WRITELN ('Введите начальное значение функции y0 при x=x0') ;
READ (y) ;
WRITELN ('Введите число значений функции на промежутке (a, b] ') ;
READ (m) ;
x := a;
h := (b - а) / m;
y1 := у;
y2 := у;
у3 := у;
WRITELN (' Метод Эйлера Метод Э. -Коши Метод Рунге-К. ') ;
WRITELN ('x=', x:5:2, ' y1=', y1:9:6, ' y2=', y2:9:6, ' y3=', y3:9:6) ;
FOR i := 1 TO m DO
BEGIN
y1 := y1 + h * f(x, y1) ;
{ < Метод Эйлера}
FOR j := 1 TO 2 DO
k0[j] := h*f(x+2*c[j] *h, y2+2*c[j] * k0[j-1] ) ;
y2 := y2 + (k0[1] + k0[2] ) / 2;
{ < Метод Эйлера-Коши}
FOR j := 1 TO 4 DO
{ < Метод Рунге-Кутта}
k[j] := h * f(x + c[j] * h, у3 + c[j] * k[j - 1] ) ;
у3 := у3 + (k[1] + 2*k[2] + 2*k[3] + k[4] ) / 6;
x := x + h;
WRITELN ('x=', x:5:2, ' y1=', y1:9:6, ' y2=', y2:9:6, ' y3=', y3:9:6) ;
END; PAUSA; END.
Қорытынды
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz