1-4 сыныптарда теңдеулер мен теңсіздіктерді енгізу, түрлендіруі және шешу әдістері


Теңдеу. Теңдеуді шешу.
Теңдеу ұғымы құрамында әріпті өрнегі (немесе әрпі) бар теңдік ретінде 1-сыныпта енгізіледі. Алдымен санды теңдіктерді теңдік құру тапсырмалары түрінде қайталау. 3 және 4 сандарының қосындасы 7-ге тең. 3+4=7;
6 және 4 сандарының айырмасы 2-ге тең 6-4=2, яғни құрамына сандар, амал таңбалары және теңдік таңбасы енетін теңдік (немесе теңдік таңбасымен осылған екі санды өрнек) ; Кейін тапсырма түрінде құрамына белгісіз сан енетін теңдіктер құрастыру. Ойлаған санды а әрпімен белгіле және жаз:
ойлаған сан мен 3-тің қосындысы 7-ге тең → а+3=7;
10 мен ойлаған санның айырмасы 1-ге тең →10-а=1;
ойлаған сан мен 2-нің айырмасы 6-ға тең → а-2=6;
Бұл өрнектерді санды өрнек деуге бола ма? (жоқ, өйткені оның құрамында әріп бар) . Бұлар теңдеулер. Нәтижесінде оқушыларда теңдеу болу үшін, әріпті өрнек пен өрнектің мәні арасында теңдік таңбасы болу керектігі туралы түсінік қалыптасады, демек, теңдеудің сол жақ және оң жақ бөлігі болады. Одан кейін оқушылар теңдіктер, теңсіздіктер және теңдеулерді әртүрлі бағандарға жазу барысында ажыратуға үйренеді.
7 + а= 9 7<9 7>2 7=7 а + 7 = 9
9 - а=7 9=9 2=2 2<9 а - 7 = 2
Теңдеумен танысқаннан кейін оқушыларда оларды шешу білігі қалыптасады:
Теңдеуді шешу-ол теңдеуді тура теңдікке айналдыратындай, а әрпінің мәндерін табу деген сөз. Төртінші сыныпта “теңдеуді шешу” ұғымын нақтылау: теңдеуді тура теңдікке айналдыратын белгісіз сан таңдеудің шешімі деп аталады. Теңдеуді шешу -оның мәнін табу деген сөз. Теңдеуді шешудің әртүрлі таныстыру.
Бірінші сыныпта -бірінші тәсіл “сынап көру”: а әрпінің орнына тура санды теңдік шыққанша, сандарды кезекпен қою; сондықтан бұл тәсілді сынап көру тәсілі дейді: 3
3 + а =7 3+0 =7 тура емес теңдік
3+1=7 тура емес теңдік
3+2=7 тура емес теңдік
3+2=7 тура емес теңдік
3+4=7 тура теңдік
демек, а=4-теңдеудің шешімі.
Екінші тәсіл теңдеулерді теңбе-тең түрлендіруге негізделген:
х + 2 =5 -теңдеудің екі бөлігінен де бірдей санды азайту: х=3 Тексеру: 3+2=55
5=5
Теңдеудің мына түрін шешумен жұмыста алдыңғыдай жүргізіледі:Х
Х • 5=10-теңдеудің екі бөлігін де бірдей санға бөлу; х=10:5-теңдеудің екі бөлігін де 5-ке бөлеміз. х=2
Тексеру:
2 х 5=10
10=10
Теңдеудің шешін тексеру былайша жүргізіледі: теңдеудегіх-тің орнына оның мәні қойылады; егер теңдеудің сол бөлігінегі санды өрнектің мәні оның оң бөлігіндегі санға тең болса, онда теңдеу дұрыс шешілген. Теңдеуді шешудің үшінші тәсілінде қосу мен азайтудың, көбейту мен бөлудің өзара кері амалдар екендігі пайлалнылады;
57- х =7, 57 санынан х-ті азайту х-ке қандай санды қосқанда, 57 шығады деген сөз. Ондай сан 7, ендеше х+7=57, осылайша таныс тәсілге яғни екі бөлігінен де бірдей санды азайтуға келтіріледі, ол сан -7. Х
Х+7=57х
х =57-7
х=50
тексеру:
50+7=57
57=57Кейбір күрделі теңдеуцлерді белгілі тәсілдерге дейін ықшамдау барысында шешіледі.
Үшінші сыныпта екінші сыныптағыға ұқсас теңдеуді шешуде белгілі тәсілді біршама қарапайым түрге келтіре отырып, күрделі теңдеулер шешуге тапсырма ұсынылады, Х
Х+2=7*9, х:2=27-20; 72:х=45:5
Төртінші сыныпта, үшінші сыныпта басталған теңдеулер ықшамдалған, содан соң әртүрлі тәсілдермен шешілетін күрделі теңдеулермен жұмыс жалғасытырылады:Х
Х*3=10*3Х
Х*3=30
І тәсіл: теңдеудің екі бөлігін д е 3-ке бөлу; х
х=30:3х
х=10
ІІ тәсіл-сынап көру тәсілі.
Мұнда теңдеуге түсіндіру сипатындағы мынадай анықтама беріледі: “Теңдеу-оның құрамына енетін өрнектің мәнін табуды қажет ететін түсінік”. Үшінші және төртінші сыныптарда 1000 көлеміндегі және көптаңбалы сандармен теңдеу енгізіледі.
Өрнектерді ықшамдау тәсілдерімен таныстыру. Қосудың ауыстырымдылық қасиеті: 380+х+620= 380+620+х=(380+620) +х= 1000+х-бастапқы өрнекті ықшамдадық, өйткені қосылғыштың орнына екеу аламыз. Көбейтудің ауыстырымдылық қасиеті: 125*х*4= көбейтудің терімділік қасиеті =125*4*х= (125*4) *х=500*х
Бастапқы өрнекті ықшамдадық, үш көбейткіштің орнына екеу алдық. Қорытынды: көптеген ажғдайларда әріпті өрнектің мәнін есептеуде, мүмкін болса, алдымен өрнекті ықшамдаймыз. Оқушылар өз беттерімен өрнектерді ықшамдайды, содан соң х =20 деп алып, өрнектің мәнін табады. Геометриялық есептерде де алгебра элементтерін қолданып, теңдеу құрып, шешу. Берілген фигуралардың периметрінөрнек түрде жазу.
Төртінші сыныпта теңдеудің түбірі, теңдеуді шешу, теңдеу түбірлерінің жиындары туралы түсінік кеңейтіледі. Х+8=12 теңдеуінің шешімі х=4, мұнда х-тің орнына басқа санды қойғанда, тура теңдік шықпайды, демек, бұл теңдеудің шешімі біреу. Теңдеудің бір немесе бірнеше шешімі болуы мүмкін. Геометриялық есептерді шығаруда теңдеулерді шығармашылық деңгейде қолданады. Теңдеулерді шешу операциясы бірнеше кезеңнен тұрады:
1) санды теңдікке көшу;
2) Теңдеуді у*а=в, х+а=в стандарт түрге келтіру, ол үшін санды теңдікке қосу не көбейтудің коммутативтік заңы немес бөлудің не азайтудың анықтамалары қолданылады. Сонда кейбір теңдеулерде х не у бірден даралануы мүмкін.
3) белгісізді даралау, . Ол үшін ақиқат санды теңдіктің екі бөлігінен де бірдей сан а алынады не екі бөлігі де бірдей сан аға бөлінеді.
4) ықшамдау және есептеулер жүргізу.
5) түбірін табу. Тексеру және жауабына жазу. Осылайша жасаудың артықшылығы оқушылардың өте жиі шатастыратын белгісіз компоненталарды табу ережесінің өзін және оны қолдануды білуінің қажеттігі болмайды, сондай-ақ бір белгісізді теңдеуді шешудегі негізгі операцияны меңгеруге себі тиеді. Біраз машықтанғаннан кейін осы операцияның кезеңдері әлдеқайда қысқартылған түрде орындалады. Мысалы түбірін тексерудің ілгеріде қажеттігі болмайдмы, белгісізді даралау операциясы ауызша түсіндііріліп сәйкес жазулар қалдырылып кетеді.
Теңдеулердің анықтамасы. Теңдеулердің түбірлері. Айнымалысы бар f (x) =g (x) теңдігі бір х айынымалы теңдеу деп аталады.
f (x) пен g (x) өрнектері мен сандық сәндер қабылдайтындай айнымасының әрбір мәні теңдеудің түбірі деп аталады. Теңдеуді шешу дегеніміз оның барлық түбірлерін табу немесе оның түбірлері жоқ екенін дәлелдеу.
1. Мысал. 3+х = 7 теңдеуінің жалғыз (бір ғана) түбірі бар: 4, өйткені айнымасының осы және тек қана осы мәнінде 3+х = 7 дұрыс теңдік болады.
2. Мысал. (х-1) (х-2) = 0 теңдеуінің екі түбірі бар: 1 мен 2.
3. Мысал. х 2 +1 = 0 теңдеуінің нақты түбірі жоқ.
Теңдеулердің жорынал түбірлері туралы да сөз етуге болатынын атап өтейік. Солай, х 2 +1 = 0 теңдеуінің екі жорамал түрібір бар.
х
1
=
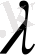 х
2
=
х
2
=
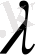 .
.
Бірдей (ортақ) түбірлері бар теңдеулер пара-пар теңдеулер деп аталады. Түбірлері жоқ болатын теңдеулер де пара-пар теңдеулер деп есептеледі.
Масалы, х+2 = 5 пн х+5 = 8 теңдеулері пара-пар, өйткені олардың әрқайсысының бір ғана (жалғыз) түбірі бар: ол 3 саны. х 2 +1 = 0 мен 2х 2 +5 = 0 теңдеулері де пара-пар - бұл теңдеулердің ешбірінің де түбірі жоқ. х-5 = 1 мен х 2 = 36 теңдеулері пара-пар емес, өйткені біріншінің тек бір х = 6 түбірі бар, ал екіншісінің екі түбірі бар: 6 мен -6.
Теңдеуді шешу процесінде оны қарапайымдау, бірақ берілгенге пара-пар теңдеулермен ауыстыруға болады. Сондықтан қандай түрлендірулер берілген теңдеулерді оған пара-пар теңдеуге көшіретінін білу маңызды.
Егер теңдеудің қандай да бір мүшесін теңдіктің бір жағынан екінші жағына таңбасын өзгертіп көшірсек, онда берілген теңдеуге пара-пар теңдеу алынады.
Мысалы, х 2 +2 = 3х теңдеуі х 2 +2- 3х = 0 теңдеуіне пара-пар.
Сызықтық теңдеулер.
Бір х айнымалысы сызықтық теңдеу деп ах = b ( а = b - нақты сандар) түбіріндегі теңдеу аталады. а-айнымасы жанындағы коэффициент, b -бос мүше деп аталады.
Сызықтық ах + b теңдеуі үшін үш жағдай болуы мүмкін
- а≠0; бұл жағдайда теңдеудің түбіріb-ға тең;
- 0; b=0 бұл жағдайда теңдеутүбірінде болады, ол кез келген х үшін дұрыс, яғни теңдеудің түбірі кез келген нақты сан;
- а=0, b≠0; бұл жағдайда теңдеутүрін қабылдайды, оның түбірлері жоқ болады.
Квадраттық теңдеулер.
а, b, с (а≠ 0 ) нақты сандар болғанда ах 2 + bх+с= 0 түріндегі теңдеу квадраттық теңдеу деп аталады. Егер а = 1 болса, онда квадраттық теңдеу келтірілген, ал егер а≠ 1 болса, онда-келтірілмеген деп аталады. а, b, с сандарының атаулары мынадай: а - бірінші коэффициент, b -екінші коэффициент, с-бос мүше.
ах 2 + bх+ с = 0 теңдеулерінің түбірлері.
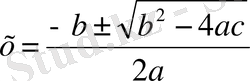
формуласы бойынша табылады.
Д
= b
2
- 4 ас
өрнегі (1) квадраттық теңдеудің, дискриминанты деп аталады. Егер
Д<0
болса, онда (1) квадраттық теңдеудің нақты түбірі жоқ; егер
Д<0
болса, онда - бір нақты түбірі бар болады.
Д<0
болған жағдайда, кейде квадраттық теңдеудің бірдей екі түбірі бар дейді.
Д
= b
2
- 4 ас
белгілеуін пайдаланып, (2) формуласын
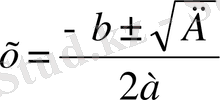 түбірінде жазуға болады. Егер
b=
2 к болса, онда (2) формуласы.
түбірінде жазуға болады. Егер
b=
2 к болса, онда (2) формуласы.
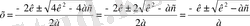 түрінде болады. Сөйтіп,
түрінде болады. Сөйтіп,
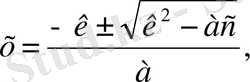
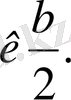
3) формуласы әсіресе
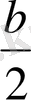 бүтін сан, яғни
b
коэффициенті жұп сан болғанда қолдауға қолайлы.
бүтін сан, яғни
b
коэффициенті жұп сан болғанда қолдауға қолайлы.
1. Мысал.
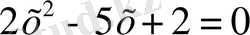 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі
а=
2,
b=
-5, с
=
2 болғандықтан
Д
= b
2
- 4 ас = (-5)
2
 Д >0
болғандықтан теңдеудің екі түбірі бар, олар (2) формуласы бойынша табамыз:
Д >0
болғандықтан теңдеудің екі түбірі бар, олар (2) формуласы бойынша табамыз:
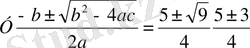 .
.
Сөйтіп,
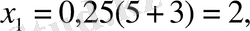
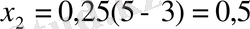 яғни
яғни
 мен
мен
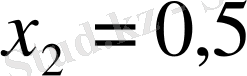 берілген теңдеудің түбірлері.
берілген теңдеудің түбірлері.
2. Мысал.
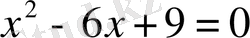 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі:
а =
1,
b =
- 6, с
=
9 болғандықтан (3) формуласы бойынша
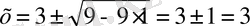 екенін табамыз. Яғни х
=
3 - теңдеудің түбірі.
екенін табамыз. Яғни х
=
3 - теңдеудің түбірі.
3. Мысал.
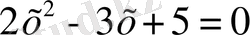 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі. а = 2, b = -3, с = 5 болғандықтан, бұл теңдеудің нақты түбірлері жоқ.
Толық емес квадраттық теңдеулер.
Егер
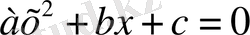 квадраттық теңдеуінде екінші коэффициент
b
және бос мүше с нольге тең болса, онда квадраттық теңдеуді толық емес деп атайды. Толық емес теңдеулерді бөліп қарастыруымыздың себебі мынада-оның түбірлерін іздегенде квадраттық теңдеудің түбірлері формуласын пайдаланбауға болады, теңдеуді оның сол жағын көбейткіштерге жіктеу әдісімен шешу ыңғайлы.
квадраттық теңдеуінде екінші коэффициент
b
және бос мүше с нольге тең болса, онда квадраттық теңдеуді толық емес деп атайды. Толық емес теңдеулерді бөліп қарастыруымыздың себебі мынада-оның түбірлерін іздегенде квадраттық теңдеудің түбірлері формуласын пайдаланбауға болады, теңдеуді оның сол жағын көбейткіштерге жіктеу әдісімен шешу ыңғайлы.
1. Мысал.
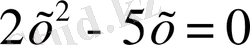 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі: х (2х - 5) бұдан не х = 0, не 2х-5 = 0, яғни х = 2, 5. Сөйтіп, теңдеудің екі түбірі бар: о мен 2, 5.
2. Мысал.
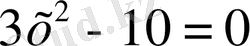 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі: Теңдеудің екі бөлігін де 3-ке бөліп,
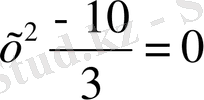 , яғни
, яғни
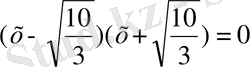 екенін аламыз. Олай болса, не
екенін аламыз. Олай болса, не
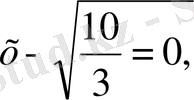 бұдан
бұдан
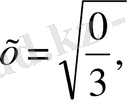 не
не
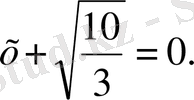 бұдан
бұдан
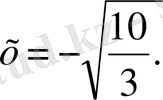 Сөйтіп теңдеудің екі түбірі бар.
Сөйтіп теңдеудің екі түбірі бар.
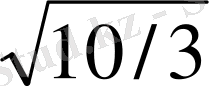 және
және
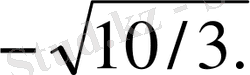
3. Мысал.
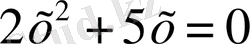 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі: Кез келген х үшін
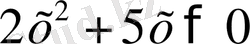 болғандықтан
болғандықтан
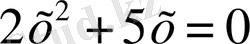 теңдеуінің түбірлері (нақты) жоқ.
теңдеуінің түбірлері (нақты) жоқ.
Теңдеулердің системалары мен жиынтықтары.
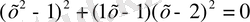 теңдеуін қарастырайық.
теңдеуін қарастырайық.
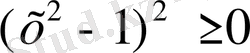 және
және
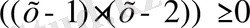 екені айқын, ол теріс емес екі санның қосындысы әр қосылғыш нольге тең болғандықтан алдымен
екені айқын, ол теріс емес екі санның қосындысы әр қосылғыш нольге тең болғандықтан алдымен
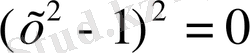 және
және
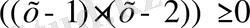 теңдеулерін шешу керек, ал содан кейін олардың ортақ түбірлерін табу керек.
теңдеулерін шешу керек, ал содан кейін олардың ортақ түбірлерін табу керек.
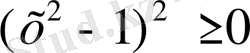 теңдеуінің түбірлері 1 мен -1 сандары, ал
теңдеуінің түбірлері 1 мен -1 сандары, ал
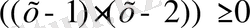 теңдеуінің түбірі 1 мен 2 сандары болады. Ортақ түбір 1 саны болады, 01-бастанқы теңдеудің түбірі.
теңдеуінің түбірі 1 мен 2 сандары болады. Ортақ түбір 1 саны болады, 01-бастанқы теңдеудің түбірі.
Берілген теңдеулердің екеуінде (бәрі де) қанағаттандыратындай айнымалының мәндерін табу керек болған жағдайда теңдеулердің системасы берілген дейді. Мысалы,
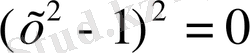 ,
,
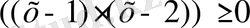 .
.
Әдетте системаның теңдеулерін бірінің астына бірін жазып, олардың алдына фигуралық жақша қояды.
Айнымалы модуль белгінің ішінде болатын теңдеулер а санының модулі былай анықталады.
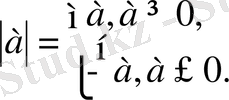
1. Мысал.
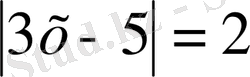 теңдеуін шешу керек.
теңдеуін шешу керек.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz