Пікірлер және оларға қолданылатын операциялар

Пікірлер және оларға қолданылатын операциялар.

Ақиқат немесе жалған екенін айтуға болатын хабарлап сөйлем пікір деп аталады.

Мысалы «Шымкент-Оңтүстік Қазақстан облысының орталығы»,

"28*18=504", "27+15>32

Айнымалылары бар және олардың нақты мәндерінде пікірге айналатын сөйлем предикат деп аталады. Мысалы "х -7=12", "х>9", "х ≤ у".

А және В пікірлерінің коньюкциясы деп, брі пікірлердің екеуі де ақиқат болғанда, тек сонда ғана ақиқат болатын пікірді айтады. Оны А ^ В таңбасы арқылы белгілеп, «А және В» деп оқиды.

А және В пікірлерінің дезъюнкциясы деп, осы пікірлердің ең болмағанда біреуі ақиқат болғанда сонда тек сонда ғана ақиқат болатын пікірді айтады, оны А в арқылы белгілеп «А немесе 3» деп оқиды.

Кейбір А пікірлерінің терістемесі деп, А пікірі ақиқат болғанда жалған, ал А жалған болғанда болатын -пікірді айтады. Оны А таңбасымен белгілейді.

А және В пікірлерінің импликациясы деп, А ақиқат және В жалған болғанда, тек сонда ғана жалған болатын пікірді айтады. Оны А => В таңбасымен белгілеп, «Егер А болса, онда В болады» деп оқиды.

А және В пікірлерінің эквиваленциясы деп, екі пікір бір мезетте, мезгілде ақиқат немесе жалған болғанда, тек сонда ғана ақиқат болатъш пікірді айтады. Оны А « В таңбасы арқылы белгілейді.

Предикаттар

Предикат ұғымы.

Екі предикаттың коньюнкциясы, оның ақиқаттық облысы

Айнымалысы бар мына төмендегі сейлемдерді қарастырайық

А) х<10

Б) х+1=7

В) х саны 5-ке қалдықсыз бөлінеді;

Г) х>у

Осы сөйлемдердегі кездесетін х және у айнымаларын тек натурал мәндерді ғана қабылдайды деп санайық, яғни Х€, N УN.

Бұл сөйлемдердін, ешқайсысы да пікір бола алмайды, себебі олардың ішінде белгісіз сандар болғандықтан, бұл сөйлемдердің ақиқаттығы туралы біз ештеңе айта алмаймыз.

Алайда, егер, мысалға, х<10 теңсіздігіндегі Х-тің орнына әр түрлі натурал сандарды қойсақ, онда біз бірде ақиқат, бірде жалған болатын натурал сандар туралы пікірлер алатынымызды байқауға болады. Шынында, егер х=12 болса 12 < 10 жалған пікір, ал егер х = 5 5<10 ақиқат предикат х<10 теңсіздігін ақиқат пікірге айналдыратын х-ің барлық натурал сан мәнінің {1, 2, 3 . . . 9} жиынында жататын көреміз. х+1=7 тендеуі х-тің кез келген натурал мәндерінде пікір бола алмайды, бірақ тек х=6 болғанда ғана ол ақиқат пікір болады.

"х саны 5-ке қалдықсыз бөлінеді" деген сөйлемде х-тің кез келген натурал мәндерінде пікір болады. Егер х-тің орнына 5, 10, 15, 20, 25, 30 т. сс сандарды қойсақ, онда бұл пікір ақиқат болады, х-тің 5-ке еселі емес мәндерінде жалған болады. " х>у" сөйлемінде екі айнымалы бар.

Ол айнымалылардың орнына натурал сандар парларын қойғазда пікірге айналады.

Мыс: х = 6 у = 4 6 > 4 ақиқат пікір

х = 3 у =5 3>5 жалған пікір.

Бір немесе бірнеше айнымалысы бар-және олардың нақтылы мәндерінде пікірге айналатын сөйлем пікірленетін форма немесе предикат деп айтылады.

Предикатқа енетін айнымалылардың сандарына қарай бір орынды, екі орынды, үш орынды т. с. с предикаттар деп ажыратылады. "х саны 5-ке қалдықсыз бөлінеді" "х<10", "х+1=7" сөйлемдері бір орынды предикаттар, ал х>у сейлемі - екі орынды предикат болады.

Осы предикаттың әрқайсысымен біз екі жиынды байланыстырдық.

Оның біріншісі N - барлық натурал сандар жиыны. Айнымалының мәндері осы жиыннан алынса берілген сөйлемдер пікірге айналады (А және Ж) .

Екіншісі - айнымалының орнына қойылғанда сөйлемдерді ақиқат пікірге айнаддыратын натурал сан жиыны.

Мыс: х<10 предикаты үшін, {1, 2 . . . 9} жиыны саналады. Бірінші жиынды предикатың анықталу (облысы) жиыны, ал екіншісін оның ақиқаттың жиыны деп атайды.

Жалпы, егер қандай да бір предикат берілген болса, онда онымен екі жиын байланысты болады.

1. Анықталу жиыны (облысы) X - айнамалының предикатты пікірге айналдыратын барлық мәндерінің жиыны.

2. Ақиқаттық облысы Т - айнымалының предикатты ақиқат пікірге айналдыратын мәндерінен тұратын жиын, әрі ТсХ.

Мысалы, "х саны 5-ке қалдықсыз бөлінеді" предикаттың анықталу облысы X болып барлық натурал сандар жиыны, Х=И, ал шындық жиын Т болып 5-ке еселі болатын барлық натурал сандар жиыны, Т = {5, 10, 15, 20, 25 . . . 5n}, n €Nболады.

Бір орынды предикатты А (х) х€Х тұрінде белгілейді. Мұндағы X -берілген предикат анықталу жиыны А (х) жазбасы "X жиынында X-тің А предикаты берілген" деп оқиды.

Егер х-тің орнына х жиынының элементтерінің бірі а-ны (а€Х) қойсақ, онда пікір аламыз және ол пікірді А (а) деп белгілейді.

Мыс: А (х), х €N"х саны 5-ке еселі" деген предикат болса, онда А (7) -"7 саны 5-ке еселі" деген пікір жалған А (60) - 60 - 5 ке еселі ақиқат пікір. Екі орынды предикатты А (х, у) тұрінде белгілейміз. Мұндағы х, у€Х.

Бастауыш сынып математикасын оқығанда біз "предикат" терминін кездестірмейміз, бірақ логика предикат деп аталатын пікірмен үнемі ісіміз болып тұрады.

а) а+ 18>23 б) а + 18 = 23 в) а+18<23

Жазбаларын қанағаттандыратын а әріпінің мәндерін

0, 1, 2, 3, 4, 5, 6, 7 сандар қатарынан алып жазыңдар

а) а+18>23 {6, 7}-шын

б) а +18=23 {5 }-шын

в) а + 18 < 23 {0, 1, 2, 3, 4} жиыны болады.

Пікір сияқты предикаттар да жай және құрама болады. Құрама предикаттар логикалық байланыс арқылы элементтер предикаттардан кұралады.

X жиынында А (х) жэне В (х) екі предикатты берілген болсын. Онда олардың конъюнкциясы болып А (х) л В (х) предикаты саналады. А (х) л В (х) предикаты X жиынының А (х) және Е (х) предикатының екеуі де ақиқат болатып х элементтері де ақиқат болады.

Мәселен, егер Х={ 1, 2, 3 . . . 11, 12} жиынында А (х) л В (х) : "X саны 7-ден кіші және жай сан" предикаты болады.

А (х) : «х саны 7-ден кіші»

А (х) : «х саны жай сан»

А(х) - предикатының ақиқаттың жиыны Ті = {1, 2, 3, 4, 5, 6} В (х) - предикатының ақиқаттың жиыныТ ₂ = {2, 3, 5, 7}. 7-ден кіші жай сан 2, 3, 5 мәндерінде ақиқат. Т, л Т ₂ {2, 3, 5}

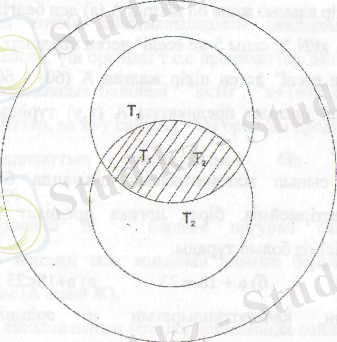
Екі предикаттың конъюнкциясының ақиқаттық кестесі

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс