Сызықтық емес регрессия және корреляция: модельдер, бағалау әдістері және қолданбалар


Тақырып 9. Сызықтық емес регрессия және корреляция.
Лекция жоспары:
- Сызықтық емес регрессиялардың түрлері.
- Тәуелділіктің параболалық түрі.
- Тәуелділіктің гиперболалық түрі.
- Тәуелділіктің экспоненциалдық түрі.
- Тәуелділіктің дәрежелік түрі.
- Сызықтық емес регрессиялардың түрлері.
Экономикалық құбылыстар арасында сызықты емес сәйкестік бар болады, олар сызықты емес функциялар көмегімен өрнектеледі.
Сызықты емес регрессияның екі түрін айыруға болады.
a) Талдауға еңгізілген ұғындыру айнымалылар арқылы сызықты емес регрессиялар, бірақ бағалау параметрлер арқылы-сызықты. Ондай регрессияға мына функциялар жатады:
- әртүрлі дәрежелі полиномдар;
- тең қабырғалы гипербола.
b) Параметрлер арқылы бағаланған сызықты емес регрессиялар.
Мұндай регрессияға келесі функциялар жатады:
- дәрежелік функция:
- көрсеткіштік функция:
- экспоненциалдық функция.
Еңгізілген айнымалы арқылы сызықты емес регрессияның параметрлерінің бағалауында еш қандай қиыншылықтар жоқ. Ол ең кіші квадраттар әдісі (ЕККӘ) арқылы анықталады, өйткені бұл функциялар параметрлер арқылы сызықты. Мысалы,
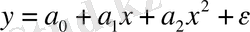 екінші ретті параболада
екінші ретті параболада
 және
және
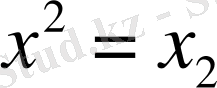 ауыстырып, екі факторлық сызықты регрессия теңдеуін аламыз:
ауыстырып, екі факторлық сызықты регрессия теңдеуін аламыз:
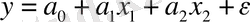 Бұл теңдеуінің параметрлерін бағалау үшін ең кіші квадраттар әдісі қолданылады. Сәйкес үшінші ретті полиномда
Бұл теңдеуінің параметрлерін бағалау үшін ең кіші квадраттар әдісі қолданылады. Сәйкес үшінші ретті полиномда
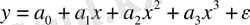 айнымалыларды ауыстырып
айнымалыларды ауыстырып

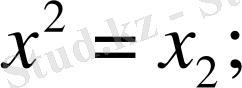
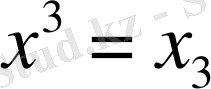 деп алсақ, онда үш факторлы сызықты регрессия теңдеуі шығады:
деп алсақ, онда үш факторлы сызықты регрессия теңдеуі шығады:
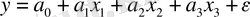 .
.
Ал, к - ретті полинам үшін
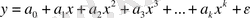
к - ұғындыру айнымалылары бар жиынды сызықтық регрессия моделі шығады:
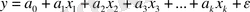
Сонымен, кез- келген ретті полиномды сызықтық регрессияға келтіруге болады.
2 . Тәуелділіктің параболалық түрі .
Зертеушілердің арасында көбінесе екінші ретті полином қолданылады.
Екінші ретті параболаның регрессия теңдеудің түрі мынадай:
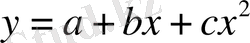
Параболалық тәуелділігінде ең кіші квадраттар әдісінің нормалдық теңдеулер жүйесі мынадай болады:
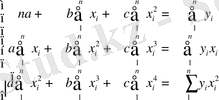
Оның шешімі Крамер әдісімен табылады:
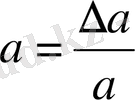 ;
;
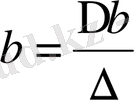 ;
;
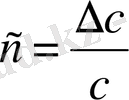 .
.
Мұнда
 -жүйенің анықтауышы;
-жүйенің анықтауышы;
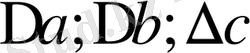 -әр параметірінің дербес анықтауыштары.
-әр параметірінің дербес анықтауыштары.
Егер b
 және с
және с
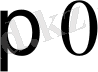 болса, ондай жағдайларда қисық жоғарғы нүкте арқылы симметриялы болады, ол байланыстың бағытын өзгертетің сынық нүктесі, атап айтқанда кемуінің өсуі. Ондай функцияны енбек экономикасында байқауға болады. Мысалы, жұмысшыларының енбек ақыларымен жас шамасыларының байланысын зерттегенде (әсіресе физикалық еңбекте) .
болса, ондай жағдайларда қисық жоғарғы нүкте арқылы симметриялы болады, ол байланыстың бағытын өзгертетің сынық нүктесі, атап айтқанда кемуінің өсуі. Ондай функцияны енбек экономикасында байқауға болады. Мысалы, жұмысшыларының енбек ақыларымен жас шамасыларының байланысын зерттегенде (әсіресе физикалық еңбекте) .
Сонда мына нәтижеге келіпті: жастың өсуімен еңбек ақысы да өседі, олармен бірге жұмыскерлердің квалификациясы да өседі. Бірақ, жастың бір кезінен бастап ағзаның қартаюіне сәйкес өнімділік еңбегі төмендейді. Сонымен, жас шамасының өсуі жұмысшының еңбек ақысының төмендеуіне келтіреді. Егер қатынастың параболалық түрі ең алдымен өсүін көрсетіп, одаң кейін нәтиже белгісінің төмендеу деңгейін көрсетсе, онда фактордың максимум мағынасы табылады.
Егер b
 және c
және c
 екінші ретті парабола өзінің төменгі нүкте арқылы симметриялы болады. Сонымен, функцияның қатынасының бағыты өзгеретін нүктедегі минимумын табуға болады, басқаша айтқанда өсуінің төмендеуін.
екінші ретті парабола өзінің төменгі нүкте арқылы симметриялы болады. Сонымен, функцияның қатынасының бағыты өзгеретін нүктедегі минимумын табуға болады, басқаша айтқанда өсуінің төмендеуін.
3. Тәуелділіктің гиперболалық түрі.
Гиперболаның регрессия теңдеуі мынадай болады:
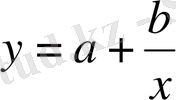
Гиперболалық регрессия теңдеуінің а және в коэффиценттердің мәндері ең кіші квадраттар әдісінің нормалдық теңдеулер жүйесінең анықталады:
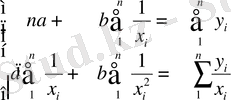
Гиперболалық тәуелділік микро -және макро деңгейлерде пайдалануы мүмкін. Мысалы, шикізаттың үлесті шығының, материалдарды, отынды өнімін өндіру көлеммен байланысып сипаттау үшін, тауар айналуы уақытын тауар айналымы шамасынан. Оның классикалық мысалы Филлипс қисығы болады, ол жұмыссыздықтың мөлшерімен еңбек ақы өсімнің пайызы арасындағы сәйкестік сипаттайды. Бағалау параметірлер арқылы сызықты емес регрессияларды қарастырайық: экспоненциалдық және дәрежелік түрлерін.
4 . Тәуелділіктің экспоненциалдық түрі .
Экспоненциалдық регрессия теңдеуінің жалпы түрі:
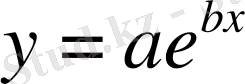 немесе
немесе
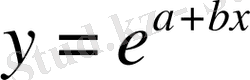 .
.
Таңдамалы жиынтықтың өңдеу алгоритімін ықшамдау үшін, экспоненциалдық регрессия теңдеуінің, берілген теңдеулердің екіншісіне, логарифімдеу жолымен сызықтандыру өткізіледі
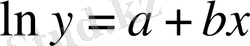 .
.
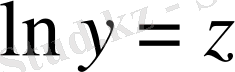 алмастыруны өткізіп, мынадай сызықты теңдеуі шығады:
алмастыруны өткізіп, мынадай сызықты теңдеуі шығады:
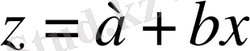 .
.
Сызықты тәуелділікке нормалдық теңдеулер жүйені қолданып
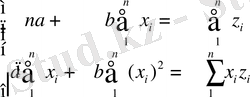
регрессия теңдеуінің
 және
және
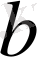 параметрлерін анықтаймыз. Кері алмастыруын жасап нәтижелік белгінің эмпирикалық мәнін табамыз.
параметрлерін анықтаймыз. Кері алмастыруын жасап нәтижелік белгінің эмпирикалық мәнін табамыз.
5. Тәуелділіктің дәрежелік түрі .
Регрессияның дәрежелік теңдеуінің жалпы түрі мынадай:
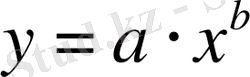
Берілген теңдеуді логарифмдеу амалы оны сызықты түрге келтіреді:
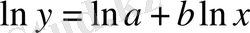 .
.
 және
және
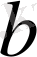 параметірлерінің бағалауын ең кіші квадраттар әдісімен табуға болады. Нормалдық теңдеулер жүйенің түрі мынадай болады:
параметірлерінің бағалауын ең кіші квадраттар әдісімен табуға болады. Нормалдық теңдеулер жүйенің түрі мынадай болады:
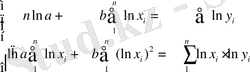
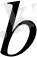 параметірі жүйеден анықталады, ал
параметірі жүйеден анықталады, ал
 парметірі
парметірі
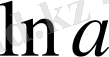 өрнекті потенциалдаумен табылады.
өрнекті потенциалдаумен табылады.
Сызықты емес корреляцияның тығыздық көрсеткіші корреляция индексі болады, оны мына формуламен анықтауға болады:
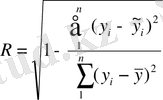
Мұнда
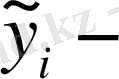 y-тің байланыс теңдеуі бойынша жекеше мәндері.
y-тің байланыс теңдеуі бойынша жекеше мәндері.
Корреляция индексі
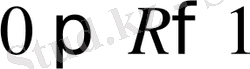 аралықта өзгереді, неғұрлым индекс бірге жақын болса, соғұрлым қарастырылған белгілердің байланысы тығыз болады, сәйкесінше табылған регрессия теңдеуінің сенімділігі жоғары болады.
аралықта өзгереді, неғұрлым индекс бірге жақын болса, соғұрлым қарастырылған белгілердің байланысы тығыз болады, сәйкесінше табылған регрессия теңдеуінің сенімділігі жоғары болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz