Ең кіші квадраттар әдісі

Пән: Экономика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Жоспар

Сызықтық регрессия моделі.
Ең кіші квадраттар әдісі.
Регрессия теңдеуінің параметрлерінің сатистикалық маңыздылығы және модельдің адекваттылығы.
Пайдаланылған әдебиеттер.

СЫЗЫҚТЫҚ РЕГРЕССИЯ МОДЕЛІ

Эконометрикалық модель - кейбір экономикалық көрсеткіштердің байланыстарын анықтайтын теңдеулер жиыны. Арақатынастар стохастикалық (кездейсоқ) және детерминалық (белгілі бір нәрсеге тәуелді) болады.

Эндогенді айнымалылар - модельдің ішінде мәндері анықталатын айнымалылар және оларды у арқылы белгілейді.

Тиімді бағалаулар - егер олар мейлінше аз дисперсия бойынша бағаланатын болса.

β - регрессия сызығының коэффициенті зерттелетін белгіні жақсартатын ең үлкен қорын сипаттайды.

Гармониялық талдау - уақыттың косинус және синус функцияларын пайдалана отырып, деңгейдің ақырғы қосындысын табу.

Регрессияның дербес теңдеулері - сызықты емес регрессия іштей сызықты, яғни көптік регрессияда сәйкес х факторынан басқаларына басқа факторларды орта деңгейде бекіткен жағдайдағы х факторы мен қорытынды белгілі байланыстарының регрессия теңдеуі.

Дербес корреляция индексі - регрессия теңдеуінің құрамына кіретін басқа факторлардың әсерін болдырмауда қорытынды мен сәйкес фактор арасындағы байланыс тығыздығын сипаттайды.

Көптік корреляция индексі - қарастырылып отырған белгі арасындағы байланыс тығыздығын сипаттайды, фактілерінің қорытындыға әсерінің тығыздығын бағалайды.

Ең кіші квадраттар әдіске сәйкес қорытынды көрсеткіштің нақты мәндерінің теориялық теңдеу бойынша алынған мәндерден ауытқуларының квадраттары қосындысының екіден артық факторларының өзара сызықты байланыста болуын көрсетеді.

Факторлар арасындағы себеп салдар байланыстары

Функционалдық тәуелділік - бір өзгермелінің мағынасына басқа өзгермелінің анықталған мағынасының сай келуі. Статистикалық (не стохастикалық, ықтималдық) тәуелділік. Коррелияциондық тәуелділік. Регрестік тәуелділік. Тәуелді және тәелсіз өзгермелілер.

Зерттеу көрсеткішінің даму динамикасы. Инерция қасиеті. Болжаудың негізгі құралы бастапқы бақылаулар бойынша алынған алғашқы параметрлер бағасы бар модель [1] . Базалық адаптивті модель болып Браун және Хольт, авторегрессия модельдері есептеледі. Браун моделі. Хольт моделі. Хольт-Уинтерс моделі. Екі және үш параметрлі модельдердің эвалюциялық әдісі. Адаптивтілік(бейімділік) сүзгілеу әдісі(БСӘ) . Гармониялық таразы әдісі.

Жұп және көптік регрессияның классикалық модельдері

Тәуелсіз айнымалылар кездейсоқ шамалар емес, ал тәуелді айнымалы шама - кездейсоқ шама себебі оның құрамына кездейсоқ шамалар кіреді. Көптік сызықтық регрессия коэффициенттерін есептеудің матрицалық формалары. Коэффициенттер дисперсиясы және стандартты қателіктер. Регрессорларды өлшеудегі қателер. ε кездейсоқ мүшесіне регрессорлар мағынасын қалыптастыратын факторлар әсер етеді. Ең кіші еселік әдісімен алынған бағалаудың стохастикалық регресорлары бар моделі. Коварияцияның ішінара бағалаулары .

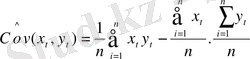Ең кіші квадраттар әдісі

Ең кіші квадраттар әдісі. 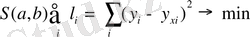формуласының дәлелдеуі. Ауытқымаған бағалар. Тиянақты бағалар. Тиімді бағалар. Стьюденттің t үлестірілімі. Ең кіші квадраттар әдісі бойынша табылған a және b бағалаулары керекті қасиеттерге ие болу үшін негізгі шарттардың орындалуы.

КӨПТІК СЫЗЫҚТЫҚ РЕГРЕССИЯ МОДЕЛІ

Интерполяция - берілгендерді өңдеу кезеңінде қолданылады және аралық ішінде жатады деп ұйғарады.

Коллинеарлы деп өзара сызықты байланыста болатын екі айнымалыны айтады.

Детерминация коэффициенті - егер фактор 1%-ға өзгерсе, қорытынды орташа пайызға өзгереді.

Сызықты емес регрессия іштей сызықты, яғни ол сәйкес түрлендірулер арқылы сыщықты түрге келтіріледі.

Сызықты емес регрессия іштей сызықты есем, яғни ол сызықты регрессияға келтірілмейді.

Экзогенді айнымалылар - модельге қарағандағы сыртқы айнымалылар, олардың мәндері модельден сыртқары анықталады. Сондықтан оларды бекітілген деп ұйғарып, әдетте, х арқылы белгілейді.

Тенденция дисперсиясы - тәжірибелік деңгеймен детерминантты қатар компоненттері арасындағы ауытқу өзгерістерінің тенденциясы.

Тренд - экономикалық көрсеткіштердің негізгі тенденциясының кездейсоқ шамаларының өзгеруінің ұзақ мерзімді тенденциясы.

Детерминация коэффициенті - егер фактор 1%-ға өзгерсе, қорытынды орташа пайызға өзгереді.

Регрессия теңдеуінің параметрлерінің сатистикалық маңыздылығы және модельдің адекваттылығы.

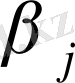коэффициентінің аралық бағасын құру. Көптік сызықтық регрессияның тәжірибелік теңдеулерінің сапасына талдау. Регрессияның бағаланған теңдеүлерінің статистикалық сапаларын төмендегі бағыттар бойынша тексереді. Регрессия теңдеулері коэффицентерінің статистикалық маңыздылығын тексеру; Регресия теңдеулерінің жалпы сапасын тексеру; Теңдеулерді бағалауда орындалды деп есептелген (ЕКӘ алғашқы шарттарының орындалуын тексеру) берілгендер қасиеттерін тексеру. Регрессия теңдеулері коэффиценттерінің статистикалық маңыздылығын тексеру. Бақылау мәні t статистиканың Стьюдент t үлестірімнің сандық нүктесі t - мен салыстыралады. Регрессия теңдеуінің жалпы тексерілуі. Көптік сызықтық регрессияның тәжірибелік теңдеулерінің сапасын талдау.

Айнымалылар ерекшелігі

Парк критерийі. Гетероскедастикалылық анықтау. 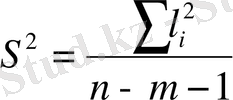айнымалылар ерекшелігі. ЕКӘ бойынша ауытқу квадратының қосындысы. Бір мезгілді теңдеулер жүйесі. Айнымалылар ерекшелігіндегі экономикалық талдау өте маңызды. Экономикалық түсініктер айнымалылар мәнділігі тыңғылықты болса, модельдің математикалық қасиеттері нашарласа да оны модельге қосуға болады деген шешімді қабылдауға мүмкіндік береді. Қарапайым түрде түсіндіруге болатын айнымалылар ерекшелігі - қарастырылатын уақыт периодында екі шама да Х және Y арасындағы корреляцияның жоғары мәнін алуға болатын уақыттық трендке ие [7-10] .

РЕГРЕССИЯНЫҢ СЫЗЫҚТЫ ЕМЕС МОДЕЛЬДЕРІ

Интерполяция - берілгендерді өңдеу кезеңінде қолданылады және аралық ішінде жатады деп ұйғарады.

Коллинеарлы деп өзара сызықты байланыста болатын екі айнымалыны айтады.

Сызықты емес регрессия іштей сызықты, яғни ол сәйкес түрлендірулер арқылы сыщықты түрге келтіріледі.

Сызықты емес регрессия іштей сызықты есем, яғни ол сызықты регрессияға келтірілмейді.

Стохастикалық модельдер зерттелетін көрстекішке кездейсоқ шамалардың әсерінің болуын білдіреді. Байланыстың мұндай түрін корреляциялық деп атайды.

Циклдік (немесе кезеңдік) тербеліс зерттеп отырған белгінің мәні белгілі уақыт аралығында өседі, максимум мәніне жетеді, қайтадан бұрыңғы мәніне дейін өседі және т. б.

Өндіріс функциясы өндірістік факторлар мен өнім шамасы арасындағы байланысты сипаттайды.

Динамика қатары (уақыт, хроникалық қатарлар) - уақыт бойынша алынған реттелген статистикалық мәліметтер.

Мерзімдік тербеліс - әрбір жылдық, айлық, күннің немесе сағаттың аралығында кезеңдік қайталанатын тербеліс.

Автокорреляция тенденциясы динамика қатарының реттелген деңгейлерінің арасындағы байланыстың өзгеруін сипаттайды.

Экономикадағы корреляция-регрессиялық талдау кезеңдері

Корреляциондық талдау мынаны қамтамасыз етеді: а) екі және оданда көп құбыластардың байланыс дәрежесін өлшеу; б) құбылыстар арасындағы байланыстылықтың дәрежесін өлшеуге негізделген, нәтижелік белгіге елеулі әсер етіп факторларды теру (таңдау) ; в) бұрын белгісіз болған байланыстарды анықтау (корреляция құбылыстардың арасынан себептік байланысты тікелей анықтамайды, бірақ бұл байланыстардың сандық мәнін және олардың бар болатындығы жайлы пікірлердің дұрыстығын орнатады. [1] Дербес коэффициент жалпылай барлық айнымалылар белгілесек деген шартпен келесі түрде есептелінеді: 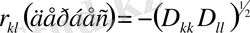. Регрессиондық талдауда келесі мәселелер шешіледі: а) тәуелділіктің формаларын орнату (оң, теріс, сызықты, сызықты емес) ; в) регрессия функциясын анықтау. Тәуелді айнымалының өзгеру тенденциясын көрсету ғана маңызды емес, сонымен қатар, егер басқа (екінші жәрежелі, кері, ) факторлар өзгермей (сол орташа деңгейде орналасса) және кездейсоқ элементтер шығарылса, онда негізгі факторлардың тәуелді айнымалыларына әсері қалай болатындығын да анықтау маңызды; в) тәуелді айнымалылардың белгісіз мәндерін бағалау. Қадамдық регрессия Y-түсіндіру үшін регрессиялардың жиынының жақсысын анықтайтын әдістердің бірі. Қадамдық регрессия теңдеуіне айнымалыларды кезектеп қосу арқылы жүзеге асады. Құлаштық регрессия мультиколлинарлық шартында, яғни тәуелсіз айнымалылардың күшті корреляциясында, жиындық сызықтық регрессияны бағалауға бағытталған, құлаштық бағалауға негізделеді.