Шектер теориясы: тізбектер мен функциялардың шектері, негізгі теоремалар мен критерийлер


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті
«Математика» кафедрасы
Курстық жұмыс
Тақырыбы: Шектер теориясы
Орындаған: Шәмшиева Г.
Ғылыми жетекші: Назарова К.
Түркістан 2012
Мазмұны
Кіріспе . . . 3
I тарау: Тізбектің шегі
1. 1 Тізбек шегін анықтау . . . . . . 4
1. 2 Шегі бар тізбектердің қасиеттері . . . 5
1. 3 Ақырсыз кішкене және ақырсыз үлкен тізбектер . . . 6
1. 4 Тізбектің шегі туралы теоремалар . . . 7
1. 5 Теңсіздіктерде шекке көшу . . . 9
1. 6 Бірсарынды тізбектер жинақталуының қажетті және жеткілікті
шарты . . . 10
1. 7 Тізбектің жинақталуының Коши критерийі . . . 11
1. 8 Тізбекшелер. Больцано-Вейерштрасс теоремасы . . . 12
1. 9 Анықталмаған өрнектер . . . 13
II тарау : Функция шегі
- Функция шегінің анықтамасы . . . ……. 14
- Бір жақты шектер . . . 15
- Функцияның шексіздіктегі шегі . . . 16
- Шегі бар функцияның шенелгендігі . . . . . . 17
- Функция шектері туралы теоремалар . . . . . . 18
- Ақырсыз кіші және ақырсыз үлкен функциялар…… . . . . 19
- Функция шегінің бар болуының қажетті және жеткілікті белгісі
(Коши критерийі) . . . . 20
- Бірсарынды функция бар болуының қажетті және
жеткілікті шарты. . 21
2. 9 Көп айнымалы функция шегі . . . 22
Қорытынды . . . 24
Пайдаланылған әдебиеттер. . 25
Кіріспе
Мен өзімнің курстық жұмысымда Шектер теориясы туралы қарастырамыз. Шектердің қазіргі теориясы 19 ғ-дың басында қалыптаса бастады. Шек ұғымы алғаш рет О. Коши еңбектерінде қолданылды. Тізбек пен функция шектерінің теориясы Б. Больцано мен К. Вейерштрасстың еңбектері негізінде қалыптасты.
Егер кез - келген оң
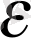 санына сәйкес натурал
санына сәйкес натурал
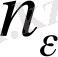 саны табылып, барлық
саны табылып, барлық
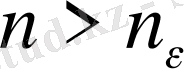 нөмірлері үшін
нөмірлері үшін
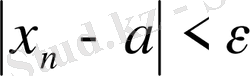 теңсіздігі орындалса, онда
a
саны
теңсіздігі орындалса, онда
a
саны
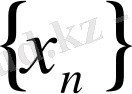 тізбегінің шегі деп аталады және былай жазылады:
тізбегінің шегі деп аталады және былай жазылады:
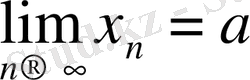
Тізбекті жазып берудің жиі қолданылатын тәсілдері мыналар:
1) Аналитикалық тәсіл. Бұл тәсілді қолданғанда n нөмері бойынша тізбектің сәйкес мүшесін табу үшін формула жазылып көрсетіледі.
2) Рекуренттік тәсіл. Бүл тәсілді қолданғанда тізбектің біріншісі беріледі және осы тізбектің белгілі бір немесе бірнеше алғашқы мүшелері бойынша кез - келген мүшесін табу үшін формула беріледі.
Мысал. а) кез - келген
n
≥ 2 үшін
a = an-1+d;
б) кез - келген
n
≥ 2 үшін
bn
=
bn-1
∙
q
; а) және б) формулалары сәйкес
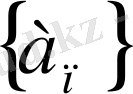 және
және
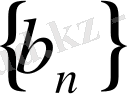 тізбектерінің берілген алдыңғы мүшесі бойынша оның кез - келген мүшесін табуға мүмкіндік береді. Тізбектің рекуренттік тәсілмен берілуі шапшаң есептейтін элетрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді.
тізбектерінің берілген алдыңғы мүшесі бойынша оның кез - келген мүшесін табуға мүмкіндік береді. Тізбектің рекуренттік тәсілмен берілуі шапшаң есептейтін элетрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді.
3) Баяндап беру тәсілі. Бұл тәсілді қолданғанда тізбек элементтері баяндап айтылатын болады. Бұл жағдайда тізбектің жалпы мүшесі үшін формула да, немесе оның мүшелері үшін рекуренттік қатыс та белгісіз болу
мүмкін. Осы айтылғанды мысалмен түсіндіру үшін мына тізбектерді қарастырайық.
а) 2, 3, 5, 7, 11, . . . ; б) 2; 2, 2; 2, 23; 2, 236; 2, 2361; . . . Бұл тізбектерді былайша баяндайды: бірінші тізбек жай сандар тізбегі, ал екіншісі -
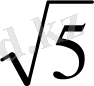 саны үшін кемімен алынған ондық жуықтаулар тізбегі.
саны үшін кемімен алынған ондық жуықтаулар тізбегі.
I тарау Тізбектің шегі
1. 1 Тізбек шегін анықтау .
Сандық тізбек деп N натурал сандар жиынында анықталған сандық функцияны атайды. Бұл функцияны f әріпімен белгілейік. Сонда анықтама бойынша 1 санына f (1) мәні, 2 санына f (2) мәні т. с. с. сәйкес келеді. Жалпы алғанда ондай сәйкестікті былай белгілейді:
n
 f (n) .
f (n) .
Бұл шамаларды сәйкес түрде
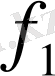 = f
(1),
= f
(1),
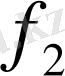 = f
(2), …,
= f
(2), …,
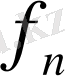 = f
(n), … арқылы белгілеп, оларды тізбектің бірінші, екінші, және т. с. с.
n
-ші мүшелері деп атайды.
n
-ші мүшені тізбектің жалпы мүшесі дейді. Тізбекті жазып берудің жиі қолданылатын тәсілдері мыналар:
= f
(n), … арқылы белгілеп, оларды тізбектің бірінші, екінші, және т. с. с.
n
-ші мүшелері деп атайды.
n
-ші мүшені тізбектің жалпы мүшесі дейді. Тізбекті жазып берудің жиі қолданылатын тәсілдері мыналар:
1) Аналитикалық тәсіл. Бұл тәсілді қолданғанда n нөмері бойынша тізбектің сәйкес мүшесін табу үшін формула жазылып көрсетіледі.
2) Рекуренттік тәсіл. Бүл тәсілді қолданғанда тізбектің біріншісі беріледі және осы тізбектің белгілі бір немесе бірнеше алғашқы мүшелері бойынша кез - келген мүшесін табу үшін формула беріледі.
Мысал. а) кез - келген
n
≥ 2 үшін
a = an-1+d;
б) кез - келген
n
≥ 2 үшін
bn
=
bn-1
∙
q
; а) және б) формулалары сәйкес
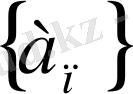 және
және
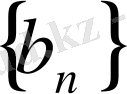 тізбектерінің берілген алдыңғы мүшесі бойынша оның кез - келген мүшесін табуға мүмкіндік береді. Тізбектің рекуренттік тәсілмен берілуі шапшаң есептейтін элетрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді.
тізбектерінің берілген алдыңғы мүшесі бойынша оның кез - келген мүшесін табуға мүмкіндік береді. Тізбектің рекуренттік тәсілмен берілуі шапшаң есептейтін элетрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді.
3) Баяндап беру тәсілі. Бұл тәсілді қолданғанда тізбек элементтері баяндап айтылатын болады. Бұл жағдайда тізбектің жалпы мүшесі үшін формула да, немесе оның мүшелері үшін рекуренттік қатыс та белгісіз болуы
мүмкін. Осы айтылғанды мысалмен түсіндіру үшін мына тізбектерді қарастырайық.
а) 2, 3, 5, 7, 11, . . . ; б) 2; 2, 2; 2, 23; 2, 236; 2, 2361; . . . Бұл тізбектерді былайша баяндайды: бірінші тізбек жай сандар тізбегі, ал екіншісі -
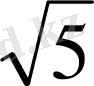 саны үшін кемімен алынған ондық жуықтаулар тізбегі.
саны үшін кемімен алынған ондық жуықтаулар тізбегі.
Тізбектердің қарапайым сипаттамалары.
а) Шенелген және шенелмеген тізбектер. Егер с > 0 саны табылып,
барлық
 үшін
үшін
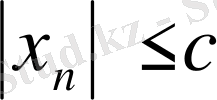 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
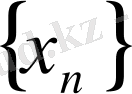 тізбегі шенелген
тізбегі шенелген
тізбек деп аталады. (символдар арқылы :
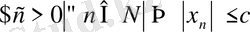 ) .
) .
Тізбектің жоғарыдан шенелгендігін символдармен жазылуын келтірейік. Егер
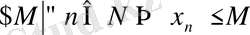 орындалса, онда
орындалса, онда
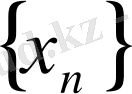 тізбегі жоғарыдан шенелген деп аталады. Сонда М саны тізбектің жоғарғы шені деп аталады. Енді тізбектің шенелгендігін терістеу арқылы оның шенелмегендігінің анықтамасын (символдар көмегімен) берейік. Егер
тізбегі жоғарыдан шенелген деп аталады. Сонда М саны тізбектің жоғарғы шені деп аталады. Енді тізбектің шенелгендігін терістеу арқылы оның шенелмегендігінің анықтамасын (символдар көмегімен) берейік. Егер
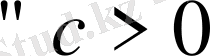 үшін
үшін
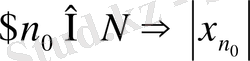 >c орындалса, онда
>c орындалса, онда
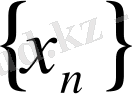 тізбегі шенелмеген деп аталады.
тізбегі шенелмеген деп аталады.
б) Тізбек үшін жұп болу, не тақ болу деген түсініктердің мағынасы болмайды, өйткені N жиыны симмметриялы емес ( N жиынына n саны енгенімен - n саны енбей отыр) .
в) Тізбек үшін периодты, не периодсыз болу деген түсініктердің де мағынасы жоқ, өйткені N жиыны периодты емес.
г)
Бірсарынды тізбектер. Барлық
n
 N
үшін
N
үшін
 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
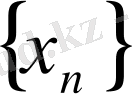 тізбегі өспелі тізбек деп аталады. Егер барлық
n
тізбегі өспелі тізбек деп аталады. Егер барлық
n
 N
үшін
N
үшін
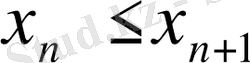 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
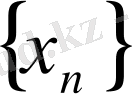 тізбегі кемімейтін тізбек деп
тізбегі кемімейтін тізбек деп
аталады. Өспелі, кемімейтін, кемімелі және өспейтін тізбектерді жалпы бірсарынды тізбектер деп атайды.
Тізбек шегін анықтау
1- анықтама.
Егер кез - келген оң
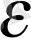 санына сәйкес натурал
санына сәйкес натурал
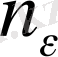 саны табылып, барлық
саны табылып, барлық
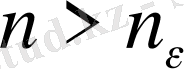 нөмірлері үшін
нөмірлері үшін
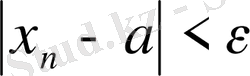 теңсіздігі орындалса, онда
a
саны
теңсіздігі орындалса, онда
a
саны
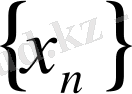 тізбегінің шегі деп аталады және былай жазылады:
тізбегінің шегі деп аталады және былай жазылады:
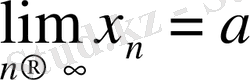 немесе
немесе
 жағдайда
жағдайда
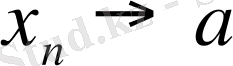 (символдар арқылы
(символдар арқылы
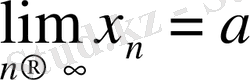
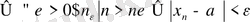 ) . Шегі бар тізбек жинақталатын тізбек деп, ал шегі болмайтын жинақталмайтын тізбек деп аталады.
) . Шегі бар тізбек жинақталатын тізбек деп, ал шегі болмайтын жинақталмайтын тізбек деп аталады.
2- анықтама
. Егер
a
нүктесінің кез - келген
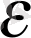 маңайы
маңайы
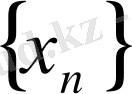 тізбегінің саны арқылы
тізбегінің саны арқылы
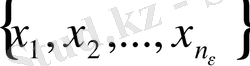 мүшелерінен өзге барлық мүшелерін қамтитын болса, онда осы
a
санын
мүшелерінен өзге барлық мүшелерін қамтитын болса, онда осы
a
санын
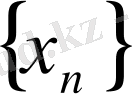 тізбегінің шегі деп атайды.
тізбегінің шегі деп атайды.
1. 2 Шегі бар тізбектердің қасиеттері
1- теорема.
Егер
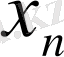 тізбегінің шегі бар болса, онда ол шек жалғыз.
тізбегінің шегі бар болса, онда ол шек жалғыз.
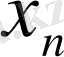 тізбегінің шегі
a
және
b
бар деп жориық. Олардың
тізбегінің шегі
a
және
b
бар деп жориық. Олардың
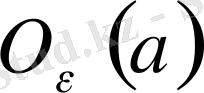 ,
,
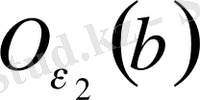 маңайларын
маңайларын
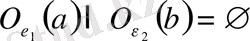 ( яғни қиылыспайтындай) етіп алайық.
( яғни қиылыспайтындай) етіп алайық.
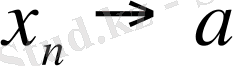 ұмтылғанда
ұмтылғанда
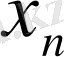 тізбегінің
тізбегінің
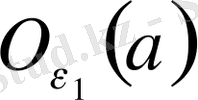 маңайының сыртында жатқан мүшелері арқылы жиын, олай болса
маңайының сыртында жатқан мүшелері арқылы жиын, олай болса
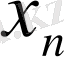 тізбегінің
тізбегінің
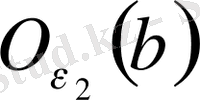 маңайында жатқан мүшелері
ақырсыз жиын бола алмайды
, сондықтан, анықтама бойынша « b» саны
маңайында жатқан мүшелері
ақырсыз жиын бола алмайды
, сондықтан, анықтама бойынша « b» саны
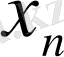 тізбегінің шегі бола алмайды.
2- теорема.
Егер
тізбегінің шегі бола алмайды.
2- теорема.
Егер
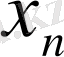 тізбегі жинақты болса, онда ол тізбек -
шенелген.
тізбегі жинақты болса, онда ол тізбек -
шенелген.
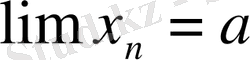 деп алайық.
деп алайық.
 саны берілсін.
саны берілсін.
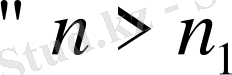 нөмерлері бар
нөмерлері бар
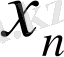 мүшелері үшін
мүшелері үшін
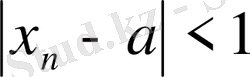 орындалатындай етіп
орындалатындай етіп
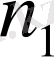 оң бүтін санын табамыз. Онда (
оң бүтін санын табамыз. Онда (
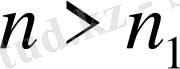 )
)
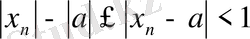 , бұдан
, бұдан
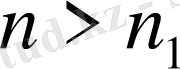 ,
,
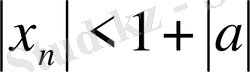 аламыз. Енді
аламыз. Енді
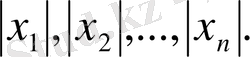 ,
,
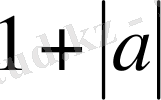 сандарының ең үлкенін
М
деп алсақ, онда
сандарының ең үлкенін
М
деп алсақ, онда

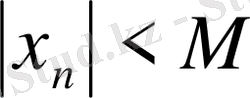 аламыз.
аламыз.
3 - теорема.
Егер
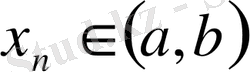 болса, онда
болса, онда
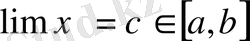
4 - теорема.
Егер
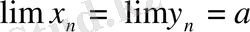 және
және
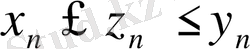 ,
n=
1, 2 . . . болса онда
,
n=
1, 2 . . . болса онда
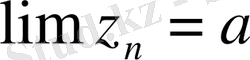
 саны берілсін. Онда
саны берілсін. Онда
 нөмірлері үшін
нөмірлері үшін
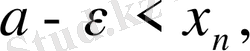
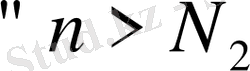 нөмірлері үшін
нөмірлері үшін

Орындалатындай
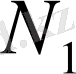 және
және
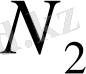 сандары табылады.
сандары табылады.
Ал
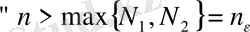 нөмірлері үшін
нөмірлері үшін
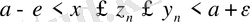
Яғни
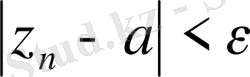 (
(
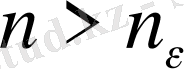 ) орындалады.
) орындалады.
5- теорема.
Егер
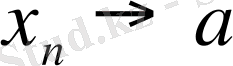 , онда
, онда
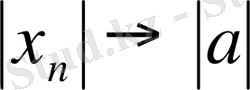 .
.
Кeлесі екі тұжырым, пара-пар: (
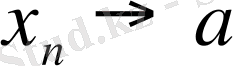 )
)
 (
(
 Оң сан берілсе
Оң сан берілсе
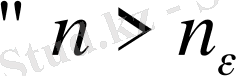 нөмірлері үшін
нөмірлері үшін
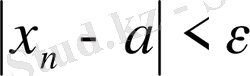 теңсіздігі орындалатындай
теңсіздігі орындалатындай
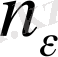 саны табылады) .
саны табылады) .
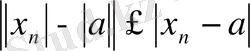 теңсіздігі орындалатыны белгілі. Олай болса
теңсіздігі орындалатыны белгілі. Олай болса
 саны берілсе
саны берілсе
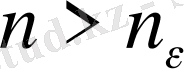 ,
,
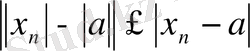
 орындалатыны
орындалатыны
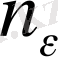 саны бар, яғни
саны бар, яғни
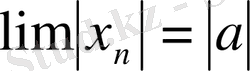
1. 3 Ақырсыз кіші және ақырсыз үлкен тізбектер.
1- анықтама
. Егер
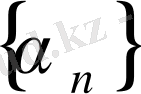 тізбегінің шегі 0 -ге тең болса, онда ол ақырсыз кіші тізбек деп аталады (
тізбегінің шегі 0 -ге тең болса, онда ол ақырсыз кіші тізбек деп аталады (
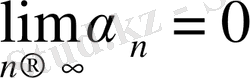 ) . Басқаша айтқанда, егер кез- келген
) . Басқаша айтқанда, егер кез- келген
 үшін,
үшін,
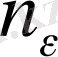 нөмірі табылып, барлық
нөмірі табылып, барлық
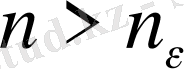 нөмірлері үшін
нөмірлері үшін
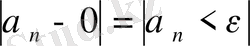 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
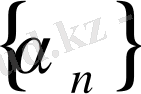 тізбегі ақырсыз кіші тізбек деп аталады (символдар арқылы
тізбегі ақырсыз кіші тізбек деп аталады (символдар арқылы
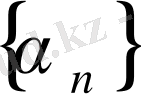 ақырсыз кіші
ақырсыз кіші
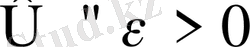
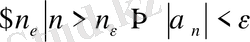 ) . Ақырсыз кіші тізбек кез - келген жинақталатын тізбек сияқты, шенелген тізбек болады.
) . Ақырсыз кіші тізбек кез - келген жинақталатын тізбек сияқты, шенелген тізбек болады.
1-теорема
.
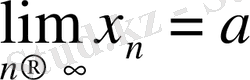 теңдігі орындалуы үшін
теңдігі орындалуы үшін
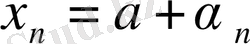 мұндағы
мұндағы
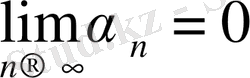 теңдігінің орындалуы қажетті және жеткілікті.
теңдігінің орындалуы қажетті және жеткілікті.
Бұл теореманы символдарды пайдаланып, дәлелдейік. Тізбектің жинақталатын болу анықтамасынан:
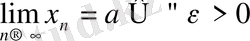
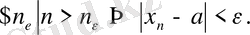
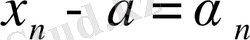
деп белгілісік,
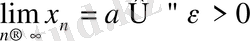
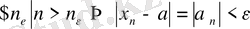 , яғни
, яғни
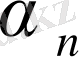 ақырсыз кіші тізбек. Демек,
ақырсыз кіші тізбек. Демек,
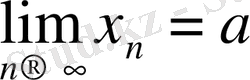

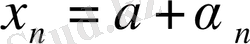 формуласын аламыз.
формуласын аламыз.
2- анықтама
. Егер кез -келген
Е>
0 санына сәйкес
 нөмірі табылып, барлық
нөмірі табылып, барлық
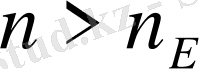 нөмірлері үшін
нөмірлері үшін
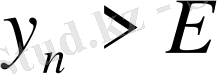 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
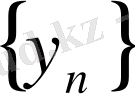 тізбегі ақырсыз үлкен тізбек деп аталады. Оны былай жазады:
тізбегі ақырсыз үлкен тізбек деп аталады. Оны былай жазады:
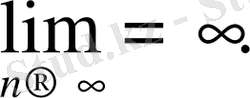 Егер ақырсыз үлкен
Егер ақырсыз үлкен
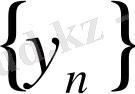 тізбегінің
тізбегінің
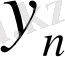 жалпы мүшесі өзінің оң (теріс) таңбасын тұрақты сақтайтын болса, (ең болмағанда жеткілікті үлкен
n
нөмірлерінен бастап), онда
жалпы мүшесі өзінің оң (теріс) таңбасын тұрақты сақтайтын болса, (ең болмағанда жеткілікті үлкен
n
нөмірлерінен бастап), онда
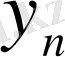 сәйкес таңбалы оң (теріс) шексіздікке ұмтылады дейді:
сәйкес таңбалы оң (теріс) шексіздікке ұмтылады дейді:
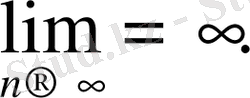
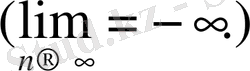 3- анықтама
. Егер кез - келген c>0 санына сәйкес
3- анықтама
. Егер кез - келген c>0 санына сәйкес
 нөмірі табылып, барлық
нөмірі табылып, барлық
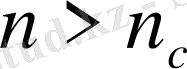 нөмірлері үшін
нөмірлері үшін
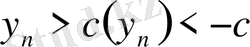 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
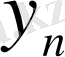 оң (теріс ) шексіздікке ұмтылады дейді және былай жазады:
оң (теріс ) шексіздікке ұмтылады дейді және былай жазады:
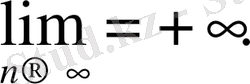
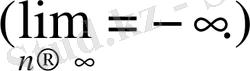
2- теорема
. Егер
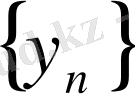 ақырсыз үлкен тізбек болса, онда
ақырсыз үлкен тізбек болса, онда
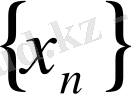
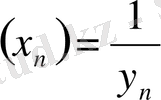 ақырсыз кіші тізбек болады. Осы тұжырымның дұрыстығын тексерейік.
ақырсыз кіші тізбек болады. Осы тұжырымның дұрыстығын тексерейік.
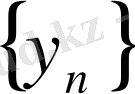 ақырсыз үлкен тізбек болсын. Анықтама бойынша кез -келген
Е>
0 саны үшін
ақырсыз үлкен тізбек болсын. Анықтама бойынша кез -келген
Е>
0 саны үшін
 нөмірі табылып, барлық
нөмірі табылып, барлық
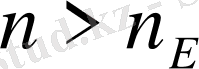 нөмірлері үшін
нөмірлері үшін
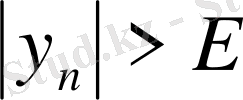 теңсіздігі орындалады. Бұдан
теңсіздігі орындалады. Бұдан
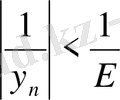 немесе
немесе
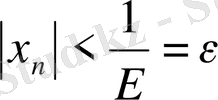 . Бұл теңсіздік барлық
. Бұл теңсіздік барлық
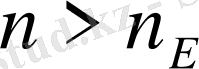 =
=
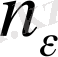 нөмірлері үшін орындалады. Соңғы теңсіздік теореманың тұжырымдамасын береді. Осыған ұқсас түрде мына тұжырымды да дәлелдеуге болады:
нөмірлері үшін орындалады. Соңғы теңсіздік теореманың тұжырымдамасын береді. Осыған ұқсас түрде мына тұжырымды да дәлелдеуге болады:
Егер
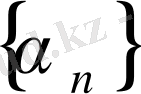
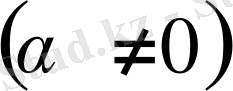 ақырсыз кіші тізбек болса, онда
ақырсыз кіші тізбек болса, онда
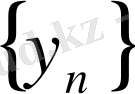 ,
,
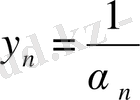 ақырсыз үлкен тізбек болады.
ақырсыз үлкен тізбек болады.
- Тізбектің шегі турлы теоремaлар.
Бұл пунктте тізбектерге арифметикалық амалдар қалай қолданылатыны жайлы әңгімеленеді.
1- теорема
. Егер
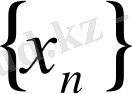 және
және
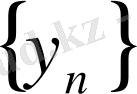 тізбектері жинақталатын болса, онда
тізбектері жинақталатын болса, онда
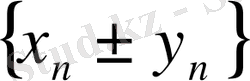 тізбектері де жинақталатын болады және
тізбектері де жинақталатын болады және
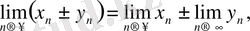 , яғни жинақталатын екі тізбек қосындысының шегі сол тізбектер шектерінің қосындысына тең болады.
, яғни жинақталатын екі тізбек қосындысының шегі сол тізбектер шектерінің қосындысына тең болады.
Дәлелдеуі
:
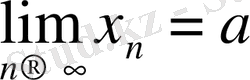 және
және
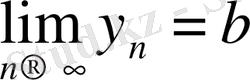 дейік. Сонда 1 - теорема негізінде
дейік. Сонда 1 - теорема негізінде
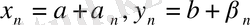 (мұндағы
(мұндағы
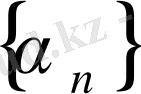 мен
мен
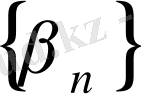 ақырсыз кіші тізбектер) теңдіктерін аламыз. Бұдан
ақырсыз кіші тізбектер) теңдіктерін аламыз. Бұдан
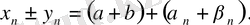
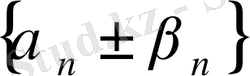 тізбегі ақырсыз кіші тізбек, яғни
тізбегі ақырсыз кіші тізбек, яғни
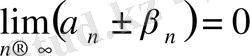 сонда 1. 3 - тің 1- теоремасы бойынша
сонда 1. 3 - тің 1- теоремасы бойынша
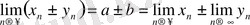 . Бұл теореманы индукция әдісін қолдана отырып, саны шектеулі тізбектердің алгебралық қосындысы үшін де дәлелдеуге болады.
. Бұл теореманы индукция әдісін қолдана отырып, саны шектеулі тізбектердің алгебралық қосындысы үшін де дәлелдеуге болады.
2- теорема
. Егер
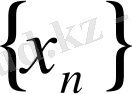 және
және
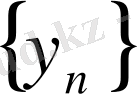 жинақталатын тізбек болса, онда
жинақталатын тізбек болса, онда
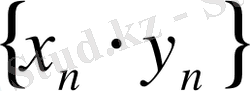 тізбегі де жинақталатын болады және
тізбегі де жинақталатын болады және
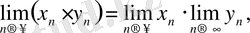 , яғни жинақталатын тізбектер көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең болады.
, яғни жинақталатын тізбектер көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең болады.
Дәлелдеуі
.
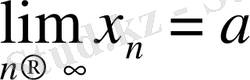 және
және
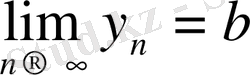 болсын, сонда
болсын, сонда
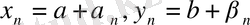 (мұндағы
(мұндағы
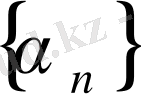 және
және
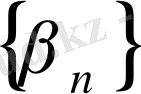 ақырсыз кіші тізбектер. ) Мына көбейтіндіні қарастырайық:
ақырсыз кіші тізбектер. ) Мына көбейтіндіні қарастырайық:
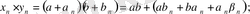
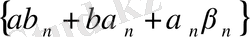
Тізбегі 1-2 леммелер негізінде ақырсыз кіші тізбек болып табылады. Сонымен, барлық
 үшін
үшін
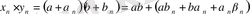
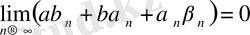 . Ал бұдан мына теңдік шығады. ( 1-теореманы қараңыз) :
. Ал бұдан мына теңдік шығады. ( 1-теореманы қараңыз) :
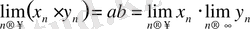
Салдар
. Егер
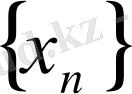 тізбегі жинақталатын болса, онда кез - келген
С
саны үшін
тізбегі жинақталатын болса, онда кез - келген
С
саны үшін
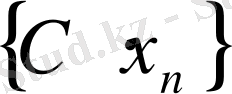 тізбегі де жинақталатын тізбек болады және
тізбегі де жинақталатын тізбек болады және
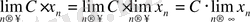 , яғни тұрақты көбейткішті шек таңбасының алдына шығаруға болады.
, яғни тұрақты көбейткішті шек таңбасының алдына шығаруға болады.
3- теорема
. Егер
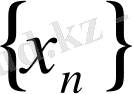 және
және
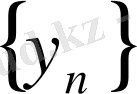 ,
,
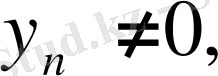 тізбектері жинақталатын болып, сонымен бірге
тізбектері жинақталатын болып, сонымен бірге
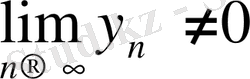 болса, онда
болса, онда
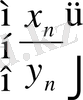 тізбегі жинақталатын болады да,
тізбегі жинақталатын болады да,
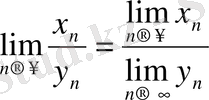 теңдігі орындалады. Алдын - ала мына лемманы дәлелдейік.
теңдігі орындалады. Алдын - ала мына лемманы дәлелдейік.
Лемма
. Егер
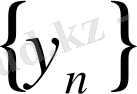 тізбегі
тізбегі
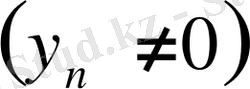 жинақталатын болып, сонымен бірге
жинақталатын болып, сонымен бірге
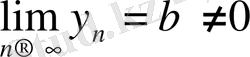 болса, онда
болса, онда
 нөмірі табылып барлық
нөмірі табылып барлық
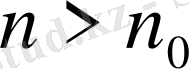 нөмірлері үшін
нөмірлері үшін
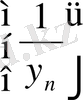 тізбегі шенделген тізбек болады.
тізбегі шенделген тізбек болады.
Дәлелдеуі. Анықтама бойынша
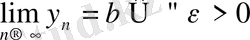
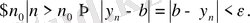
Енді
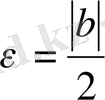 деп алып, айырма модулінің қасиетін пайдаланып, алдыңғы теңсіздікті мына түрде жазайық:
деп алып, айырма модулінің қасиетін пайдаланып, алдыңғы теңсіздікті мына түрде жазайық:
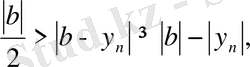 (
(
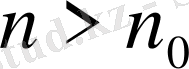 ) . Бұдан
) . Бұдан
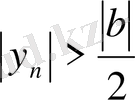 теңсіздігі шығады, ал шарт бойынша
теңсіздігі шығады, ал шарт бойынша
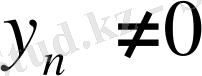 болғандықтан, барлық
болғандықтан, барлық
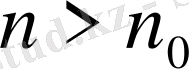 нөмірлері үшін
нөмірлері үшін
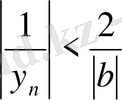 теңсіздігі орындалады.
теңсіздігі орындалады.
3- теореманы дәлелдеуге көшейік.
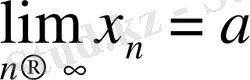 ,
,
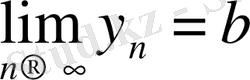 деп алайық. Теореманы дәлелдеу үшін (1. 3 1- теоремасы бойынша)
деп алайық. Теореманы дәлелдеу үшін (1. 3 1- теоремасы бойынша)
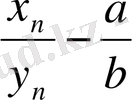 айырымы ақырсыз кіші екенін дәлелдеу жеткілікті. Бізге мына теіңдіктер белгілі :
айырымы ақырсыз кіші екенін дәлелдеу жеткілікті. Бізге мына теіңдіктер белгілі :
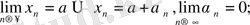
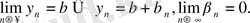
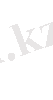
Осылдарды пайдаланып табатынымыз :
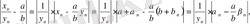 ,
,
Мұндағы
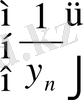 тізбегі лемма бойынша шенелген, ал ақырсыз кіші тізбек. Сондықтан
тізбегі лемма бойынша шенелген, ал ақырсыз кіші тізбек. Сондықтан
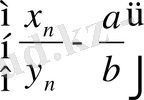 айырымы ақырсыз кіші тізбек болады. Бұдан мына теңдік шығады. (6п. 1- теорема) :
айырымы ақырсыз кіші тізбек болады. Бұдан мына теңдік шығады. (6п. 1- теорема) :
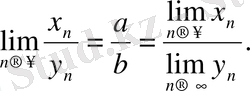
1. 5 Теңсіздіктерде шекке көшу
Теорема.
Егер
 жағдайда
жағдайда
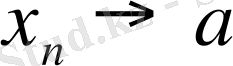 ,
,
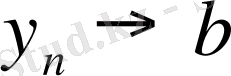 және де барлық
және де барлық
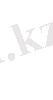
 нөмірлері үшін
нөмірлері үшін
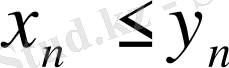 болса, онда
болса, онда
 . Қысқаша айтқанда, алынған теңсіздікте шекке көшуге болады.
. Қысқаша айтқанда, алынған теңсіздікте шекке көшуге болады.
Дәлелдеуі.
Қарсы жорып,
a>b
дейік.
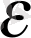 санын мына аралықтан 0<
санын мына аралықтан 0<
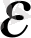 <
<
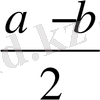 таңдап алайық. Тізбек шегінің анықтамасы бойынша осы
таңдап алайық. Тізбек шегінің анықтамасы бойынша осы
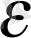 санына сәйкес натурал
санына сәйкес натурал
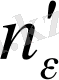 саны табылып, барлық
саны табылып, барлық
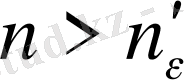 нөмірлері үшін
нөмірлері үшін
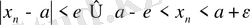 теңсіздігі орындалады. Осыған ұқсас түрде алынған
теңсіздігі орындалады. Осыған ұқсас түрде алынған
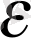 санына сәйкес натурал
санына сәйкес натурал
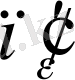 саны табылып, барлық
саны табылып, барлық
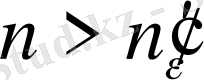 нөміллері үшін
нөміллері үшін
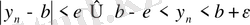 теңсіздігі орындалады. Егер
теңсіздігі орындалады. Егер
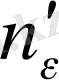 және
және
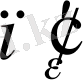 сандарының ең үлкенін
сандарының ең үлкенін
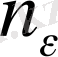 арқылы белгілесек, онда
арқылы белгілесек, онда
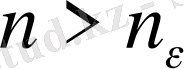 нөмірлері үшін осы теңсіздіктердің екеуі де сөзсіз орындалады. Сонда
нөмірлері үшін осы теңсіздіктердің екеуі де сөзсіз орындалады. Сонда
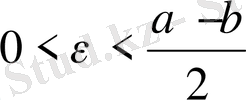 теңсіздігін түрлендіре келе, табатынымыз:
теңсіздігін түрлендіре келе, табатынымыз:
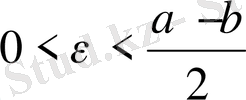
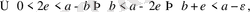
яғни

Барлық
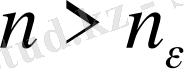 нөмірлері үшін соңғы теңсіздіктерден
нөмірлері үшін соңғы теңсіздіктерден
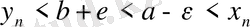 , нeмесе
, нeмесе
 теңсіздігі шығады. Алайда, бұл теңсіздік теореманың шарты
теңсіздігі шығады. Алайда, бұл теңсіздік теореманың шарты
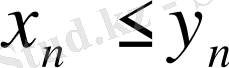 теңсіздігіне қайшы. Демек,
a>b
деп жору қате. Сондықтан
теңсіздігіне қайшы. Демек,
a>b
деп жору қате. Сондықтан
 болады ( яғни теңсіздікте шекке көшуге болады.
болады ( яғни теңсіздікте шекке көшуге болады.
- Бірсарынды тізбектер жинақталуының қажетті және жеткілікті шарттары
1 - теорема
. Егер
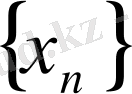 тізбегі кемімейтін болып және жоғарыдан қандай да бір
В
санымен шенелген болса, онда ол тізбек жинақталады және оның шегі
М
саны
В
санынан артық болмайды, яғни
тізбегі кемімейтін болып және жоғарыдан қандай да бір
В
санымен шенелген болса, онда ол тізбек жинақталады және оның шегі
М
саны
В
санынан артық болмайды, яғни
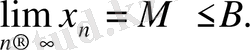
Дәлелдеуі.
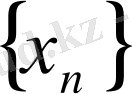 жоғарыдан шенделген тізбек, сондықтан оны жоғарыдан шенделген бос емес жиын деп қарастырайық., оның дәл жоғарғы шені
М
бар болады. Енді осы
М
саны
жоғарыдан шенделген тізбек, сондықтан оны жоғарыдан шенделген бос емес жиын деп қарастырайық., оның дәл жоғарғы шені
М
бар болады. Енді осы
М
саны
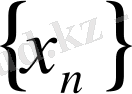 тізбегінің шегі болатынын дәлелдейік:
тізбегінің шегі болатынын дәлелдейік:
 болғандықтан, кез - келген
болғандықтан, кез - келген
 үшін
үшін
 табылып,
табылып,
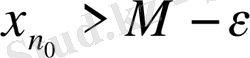 теңсіздігі орындалады.
теңсіздігі орындалады.
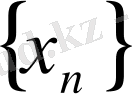 кемімейтін тізбек болғандықтан, барлық
кемімейтін тізбек болғандықтан, барлық
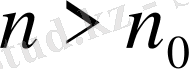 үшін бұл теңсіздік негізінде
үшін бұл теңсіздік негізінде
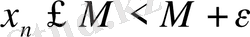 . Ал
. Ал
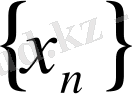 тізбегінің кез - келген мүшесі өзінің дәл жоғарғы шекарасынан артпайтын болғандықтан, барлық
тізбегінің кез - келген мүшесі өзінің дәл жоғарғы шекарасынан артпайтын болғандықтан, барлық
 үшін
үшін
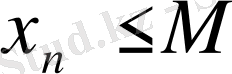 және кез -келген
және кез -келген
 үшін
үшін
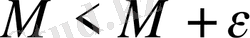 . сондықтан,
. сондықтан,
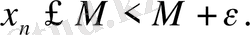 . Алайда соңғы теңсіздіктерді біріктіргенде шығатын
. Алайда соңғы теңсіздіктерді біріктіргенде шығатын
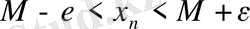 теңсіздігі барлық
теңсіздігі барлық
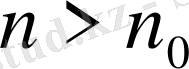 үшін орындалады, яғни
үшін орындалады, яғни
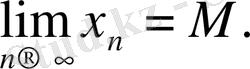 . Әрине,
. Әрине,
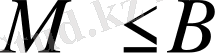 ( дәл жоғарғы шек барлық басқа жоғарғы шектердің ең кішісі ) болатыны түсінікті
( дәл жоғарғы шек барлық басқа жоғарғы шектердің ең кішісі ) болатыны түсінікті
2- теорема
. Егер
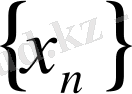 тізбегі өспейтін тізбек болып және төменнен қандай болса да бір
А
санымен шенелген болса, онда ол тізбек жинақталады және оның шегі
т
саны
А
санынан кем болмайды, яғни
тізбегі өспейтін тізбек болып және төменнен қандай болса да бір
А
санымен шенелген болса, онда ол тізбек жинақталады және оның шегі
т
саны
А
санынан кем болмайды, яғни
 .
.
Ескерту . Кемімейтін тізбек төменнен шенелген (мысалы, өзінің бірінші мүшесімен) тізбек болады. Сондықтан, егер кемімейтін тізбек жоғарыдан шенелген болса, онда екі жағынан да шенеледі, яғни шенелген.
3 - теорема. Бірсарынды тізбек жинақталуы үшін, оның шенелген
болуы қажетті және жеткілікті.
Дәлелдеуі. Қажеттілік
. Бірсарынды
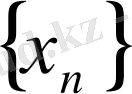 тізбегі жинақталады. Ал жинақталатын тізбектің шенелген болатыны белгілі.
тізбегі жинақталады. Ал жинақталатын тізбектің шенелген болатыны белгілі.
Жеткіліктілік:
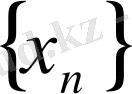 тізбегі бірсарынды, әрі шенделген болсын. Сонда тізбектің шегінің бар болуы, не 1 - теоремадан ( егер
тізбегі бірсарынды, әрі шенделген болсын. Сонда тізбектің шегінің бар болуы, не 1 - теоремадан ( егер
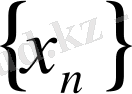 кемімейтін тізбек болса) , не 2 - теоремадан ( егер
кемімейтін тізбек болса) , не 2 - теоремадан ( егер
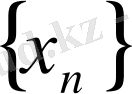 өспейтін тізбек болса) шығады.
өспейтін тізбек болса) шығады.
1. 7 Тізбектің жинақталуының Коши критерийі.
Егер кез - келген оң
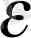 саны үшін натурал
саны үшін натурал
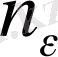 саны табылып,
саны табылып,
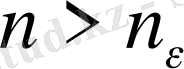 және
және
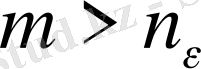 шарттарын қанағаттандыратын барлық
шарттарын қанағаттандыратын барлық
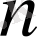 және
және
 натурал сандары үшін
натурал сандары үшін
 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
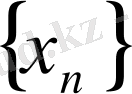 тізбегін негізгі (фундаментальдық) тізбек деп атайды.
тізбегін негізгі (фундаментальдық) тізбек деп атайды.
Коши критерийі
.
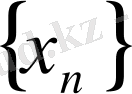 тізбегі жинақталуы үшін, оның негізгі тізбек болуы қажетті және жеткілікті.
тізбегі жинақталуы үшін, оның негізгі тізбек болуы қажетті және жеткілікті.
Дәлелдеуі. Қажеттілік.
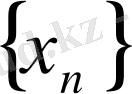 жинақталатын тізбек және
жинақталатын тізбек және
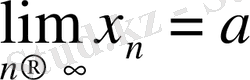 болсын.
болсын.
 Жинақталатын тізбектің анықтамасы бойынша кез - келген
Жинақталатын тізбектің анықтамасы бойынша кез - келген
 санын
санын
сәйкес натурал
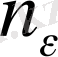 саны табылып, барлық
саны табылып, барлық
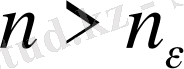 үшін
үшін
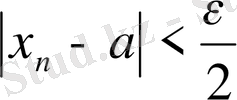 теңсіздігі және осыған ұқсас түрде
теңсіздігі және осыған ұқсас түрде
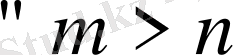 үшін
үшін
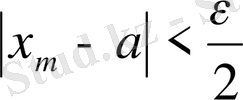 теңсіздігі орындалады. Осы
теңсіздігі орындалады. Осы
теңсіздіктерге сүйеніп және қосынды модулінің қасиетін пайдаланып барлық
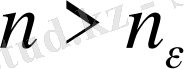 және
және
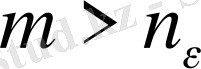 үшін былай жазамыз:
үшін былай жазамыз:
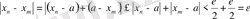
Яғни
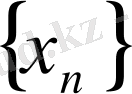 негізгі тізбек болады.
негізгі тізбек болады.
Жеткіліктілік.
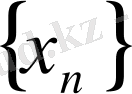 тізбегі негізгі тізбек болсын.
тізбегі негізгі тізбек болсын.
 деп алып, оған сәйкес
деп алып, оған сәйкес
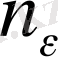 табайық. Сонда барлық
табайық. Сонда барлық
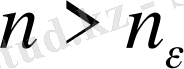 ,
,
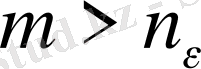 үшін
үшін
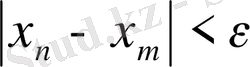 теңсіздігі орындалады.
теңсіздігі орындалады.
 дейік. Сонда
дейік. Сонда
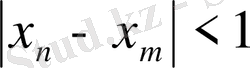 .
.
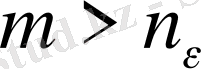 нөмірін бекітіп алып, айырым модулінің қасиетін пайдаланып, алдыңғы теңсіздікті былай жазамыз:
нөмірін бекітіп алып, айырым модулінің қасиетін пайдаланып, алдыңғы теңсіздікті былай жазамыз:
 . Сонда барлық
. Сонда барлық
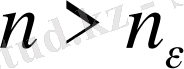 үшін
үшін
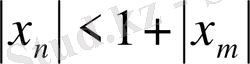 теңсіздігі орындалады, яғни
теңсіздігі орындалады, яғни
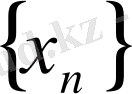 шенделген тізбек балады. ( яғни
шенделген тізбек балады. ( яғни
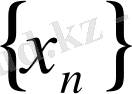 тізбегінің барлық мүшесін қамтитын сан түзуінің кесіндісін табуға болады) .
тізбегінің барлық мүшесін қамтитын сан түзуінің кесіндісін табуға болады) .
 нөмірлі барлық
нөмірлі барлық
 мүшелерін қамтитын ең кіші кесіндіні
мүшелерін қамтитын ең кіші кесіндіні
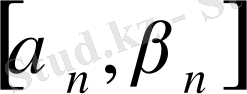 арқылы белгілейік.
арқылы белгілейік.
Ол үшін
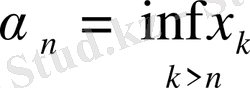 ,
,
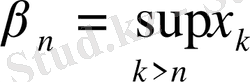
Деп алу жеткілікті, яғни
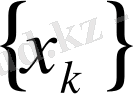
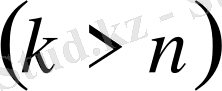 жиынының дәл жоғарғы және дәл төменгі шенін
жиынының дәл жоғарғы және дәл төменгі шенін
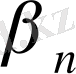 мен
мен
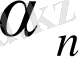 деп алу керек. Енді
деп алу керек. Енді
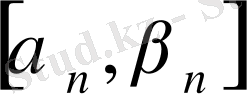 ,
,

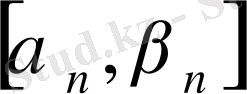 кесіндісінің ұзындығы
кесіндісінің ұзындығы
 жағдайда 0-ге ұмтылатынын тексерейік. Негізгі тізбек анықтамасы бойынша кез - келген
жағдайда 0-ге ұмтылатынын тексерейік. Негізгі тізбек анықтамасы бойынша кез - келген
 санына
санына
сәйкес
 саны табылып, барлық
саны табылып, барлық
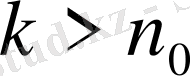 нөмірлері үшін
нөмірлері үшін
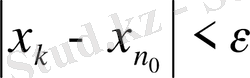 немесе
немесе
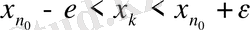 теңсіздігі орындалады. Осыған ұқсас түрде
теңсіздігі орындалады. Осыған ұқсас түрде
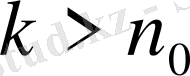 нөмірлі
нөмірлі
барлық
 мүшелерін қамтитын ұзындығын ең кіші
мүшелерін қамтитын ұзындығын ең кіші
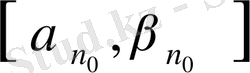 кесіндісінің ұштары үшін де
кесіндісінің ұштары үшін де
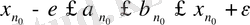 . Бұдан
. Бұдан
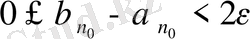 .
.
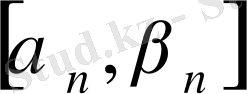 кесінділері бірінің ішінде бірі орналасқандықтан, барлық
кесінділері бірінің ішінде бірі орналасқандықтан, барлық
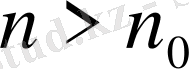 үшін
үшін
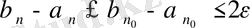 , яғни
, яғни
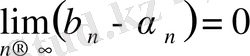 . Сонымен, бірінің ішіне бірі орналасқан кесіндіер принципі орындалатын болды. ( 3-теореманың салдары) . Олай болса барлық
. Сонымен, бірінің ішіне бірі орналасқан кесіндіер принципі орындалатын болды. ( 3-теореманың салдары) . Олай болса барлық
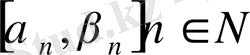 кесінділеріне ортақ бір ғана ɑ нүктесі табылады. Енді
кесінділеріне ортақ бір ғана ɑ нүктесі табылады. Енді
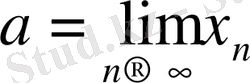 екендігін дәлелдейік. ɑ нүктесін қамтитын (c, d) интервалын қарастырайық. Сонда бұл маңайдың
екендігін дәлелдейік. ɑ нүктесін қамтитын (c, d) интервалын қарастырайық. Сонда бұл маңайдың
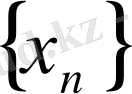 тізбегінің ақырсыз көп нүктелерін қамтитындығын тексеру жеткілікті . Бұны орындау қиын емес. Шынында да (
тізбегінің ақырсыз көп нүктелерін қамтитындығын тексеру жеткілікті . Бұны орындау қиын емес. Шынында да (
 Жағдайда
Жағдайда
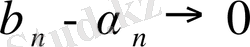 болатындықтан ), натурал
болатындықтан ), натурал
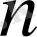 саны табылып,
саны табылып,
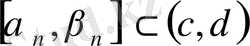 екенін қашанда көрсетуге болады. Олай болса, барлық
екенін қашанда көрсетуге болады. Олай болса, барлық
 нөмірлері үшін
нөмірлері үшін
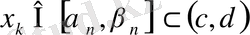 орындалады, ендеше
орындалады, ендеше
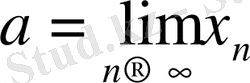
1. 8 Тізбекшелер. Больцано - Вейерштрасс теоремасы.
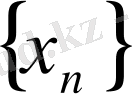 тізбегі берілсін:
тізбегі берілсін:
 . ол тізбекке енетін
. ол тізбекке енетін
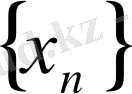
 тізбекшесін қарастырайық:
тізбекшесін қарастырайық:
 , мұндағы
, мұндағы
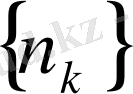 натурал сандардың қандай болса да бір өспелі жиыны, яғни
натурал сандардың қандай болса да бір өспелі жиыны, яғни
 Егер
Егер
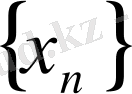 тізбегі жинақталатын болса, оның тізбекшесі
тізбегі жинақталатын болса, оның тізбекшесі
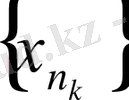 да жинақталады және оның шегі
да жинақталады және оның шегі
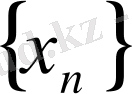 тізбегінің шегіне тең болады. Осылайша, егер
тізбегінің шегіне тең болады. Осылайша, егер
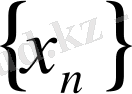 ақырсыз үлкен тізбек болса, онда
ақырсыз үлкен тізбек болса, онда
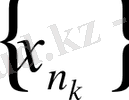 тізбегі де ақырсыз үлкен тізбек болады. Алайда,
тізбегі де ақырсыз үлкен тізбек болады. Алайда,
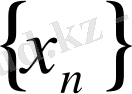 тізбегінің шегі болмағанда оның
тізбегінің шегі болмағанда оның
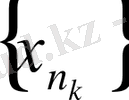 тізбекшесінің шегі де болмайды деген қорытынды шықпайды.
тізбекшесінің шегі де болмайды деген қорытынды шықпайды.
Больцано - Вейерштрасс теоремасы . Кез - келген шенелген тізбектен жинақталатын тізбекше бөліп шығаруға болады.
Дәлелдеуі:
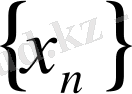 шенелген тізбек, яғни
шенелген тізбек, яғни
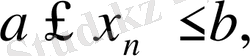
 болсын.
болсын.
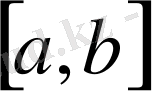 кесіндісін қақ бөлейік. Сонда осы кесінділердің ең болмағанда бірі
кесіндісін қақ бөлейік. Сонда осы кесінділердің ең болмағанда бірі
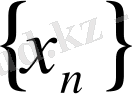 тізбегінің ақырсыз көп мүшелерін қамтиды ( олай болмағанда
тізбегінің ақырсыз көп мүшелерін қамтиды ( олай болмағанда
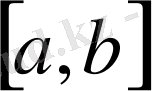 кесіндісі қамтитын
кесіндісі қамтитын
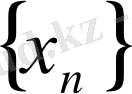 мүшелерінің саны шектеулі болар еді) ;
мүшелерінің саны шектеулі болар еді) ;
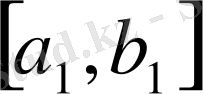 кесінді
кесінді
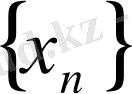 тізбегінің ақырсыз көп мүшелерін қамтитын кесінді болсын. ( егер екі кесіндінің әр қайсысы да, ақырсыз көп мүше қамтитын болса, онда олардың кез - келгенін алуға болады) . Енді
тізбегінің ақырсыз көп мүшелерін қамтитын кесінді болсын. ( егер екі кесіндінің әр қайсысы да, ақырсыз көп мүше қамтитын болса, онда олардың кез - келгенін алуға болады) . Енді
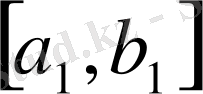 кесіндісін де осылайша қақ бөліп,
кесіндісін де осылайша қақ бөліп,
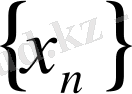 тізбегінің ақырсыз көп мүшелерін қамтитын бөлігін
тізбегінің ақырсыз көп мүшелерін қамтитын бөлігін
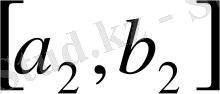 арқылы белгілейік. Осы процесті жалғастыра келе
арқылы белгілейік. Осы процесті жалғастыра келе
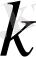 қадам жасап, ол тізбектің ақырсыз көп мүшелерін қамтитын
қадам жасап, ол тізбектің ақырсыз көп мүшелерін қамтитын
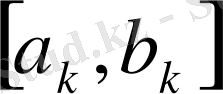 кесіндісін бөліп аламыз. Сонда ұзындығы 0- ге ұмтылатын (
кесіндісін бөліп аламыз. Сонда ұзындығы 0- ге ұмтылатын (
 жағдайда
жағдайда
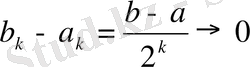 )
)
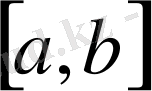

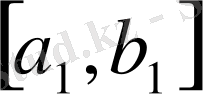

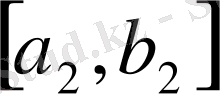
 . . .
. . .

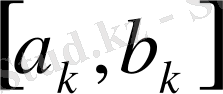
 . . .
. . .
кесінділер жүйесін аламыз. Демек, бірі бірінің ішіне орналасқан кесінділер принципі негізінде
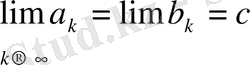 (*)
(*)
Енді берілген
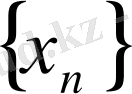 тізбегінен
тізбегінен
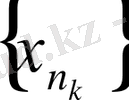 тізбекшесін былайша бөліп шығарамыз:
тізбекшесін былайша бөліп шығарамыз:
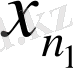 үшін
үшін
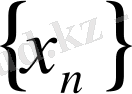 тізбегінің
тізбегінің
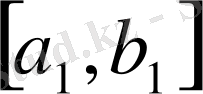 кесіндісі қамтитын кез - келген мүшесін аламыз. Процесті осылайша әрі қарай жалғастыра отырып, k қадам жасап,
кесіндісі қамтитын кез - келген мүшесін аламыз. Процесті осылайша әрі қарай жалғастыра отырып, k қадам жасап,
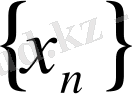 тізбегінің
тізбегінің
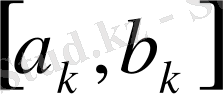 кесіндісі қамтитын
кесіндісі қамтитын
 мүшесін аламыз., т. с. с. демек,
мүшесін аламыз., т. с. с. демек,
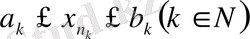 . Бұдан алдыңғы теңдікпен (*) тізбек
. Бұдан алдыңғы теңдікпен (*) тізбек
жинақталуының жеткілікті шарты бойынша
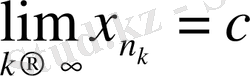 теңдігін аламыз. Яғни
теңдігін аламыз. Яғни
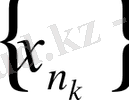 тізбекшесі жинақталады.
тізбекшесі жинақталады.
1. 9 Анықталмаған өрнектер.
1) Егер
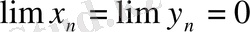
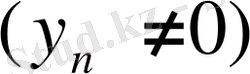 болса, онда
болса, онда
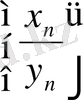 тізбегінің шегі туралы алдын - ала анық ешнәрсе айта алмаймыз. Мысалы, егер
тізбегінің шегі туралы алдын - ала анық ешнәрсе айта алмаймыз. Мысалы, егер
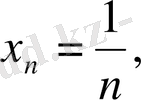
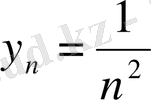 болса, онда
болса, онда
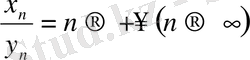 ; егер
; егер
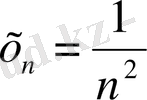 ,
,
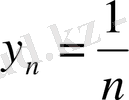 болса, онда
болса, онда
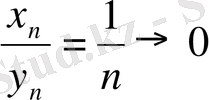
 егер
егер
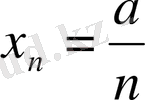 ,
,
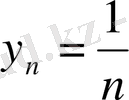 болса, онда
болса, онда
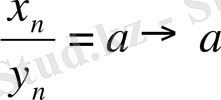 (
(
 ) ; егер
) ; егер
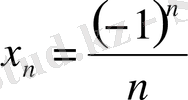 ,
,
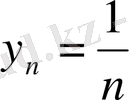 Equation. 3 болса, онда
Equation. 3 болса, онда
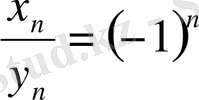 шегі жоқ.
шегі жоқ.
Сонымен,
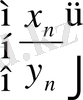 шегін табу үшін
шегін табу үшін
 ,
,
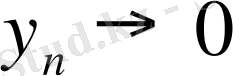 болатынын білу жеткіліксіз. Бұл жағдайда
болатынын білу жеткіліксіз. Бұл жағдайда
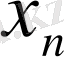 мен
мен
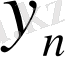 айнымалыларының өзгерістерін сипаттайтын қосымша мәліметтер қажет немесе
айнымалыларының өзгерістерін сипаттайтын қосымша мәліметтер қажет немесе
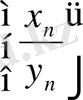 шегін табуға арнайы тәсілдер қоллдану қажет. Егер
шегін табуға арнайы тәсілдер қоллдану қажет. Егер
 ,
,
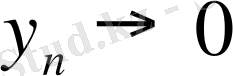 нөлге ұмтылатын болса, онда
нөлге ұмтылатын болса, онда
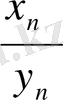 өрнегі
өрнегі
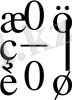 түріндегі
анықталмаған өрнек
деп аталады.
түріндегі
анықталмаған өрнек
деп аталады.
Анықталмаған өрнектердің кейбіреулерін атап өтейік . Егер:
2)
 ,
,
 болса, онда
болса, онда
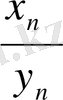 өрнек,
өрнек,
 түріндегі;
түріндегі;
3)
 ,
,
 болса, онда
болса, онда
 өрнек
өрнек
 түріндегі;
түріндегі;
4)
 ,
,
 болса, онда
болса, онда
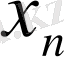 +
+
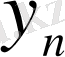 өрнек
өрнек

5)

 болса, онда
болса, онда
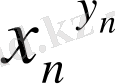 өрнегі
өрнегі
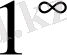 түіндегі анықталмаған өрнектер деп аталады.
түіндегі анықталмаған өрнектер деп аталады.
II тарау Функция шегі
2. 1 Функция шегінің анықтамасы
а нүктесінің қандай болмасын (с, d ) маңайында ( мүмкін а нүктесінде де ) анықталған ƒ функциясын қарастырайық.
1
-
анықтама.
Егер a санына жинақталатын кез келген
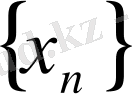 тізбегі (мұның ешбір элементі
тізбегі (мұның ешбір элементі
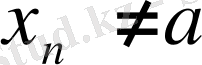 ) үшін ƒ функциясы мәндерінің сәйкес
) үшін ƒ функциясы мәндерінің сәйкес
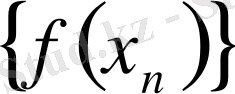 тізбегі
тізбегі
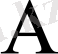 санына жинақталатын болса, онда A санын ƒ функциясының
санына жинақталатын болса, онда A санын ƒ функциясының
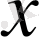 -
тің
а
-
ға ұмытылғандағы шегі деп атайды және былай белгілейді:
-
тің
а
-
ға ұмытылғандағы шегі деп атайды және былай белгілейді:
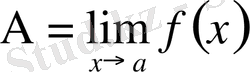
немесе
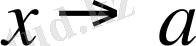 жағдайда
жағдайда
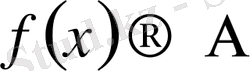 (символдар арқылы:
(символдар арқылы:
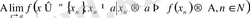 ) .
) .
Егер нүкте маңайының (жеке жағдайда ортасынан тесілген) белгілеуін пайдалансақ, былай жаазуға болады:
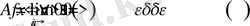
 , яғни кез- келген
, яғни кез- келген
 үшін
үшін
 саны табылып, аргумент мәндері
а
нүктесінің ортасынан (тесілген)
саны табылып, аргумент мәндері
а
нүктесінің ортасынан (тесілген)
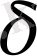 маңайына тиісті болғанда
f
функциясының сәйкес мәндері А нүктесінің
маңайына тиісті болғанда
f
функциясының сәйкес мәндері А нүктесінің
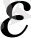 маңайына ( у өсі бойында) тиісті болады (1- сурет)
маңайына ( у өсі бойында) тиісті болады (1- сурет)

2. 2 Бір жақты шектер.
ƒ функциясы (с,
d
] жарты интервалда (мүмкін
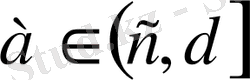 нүктесінде де) анықталған дейік.
нүктесінде де) анықталған дейік.
1
-
анықтама.
Егер
а
санына жинақталатын кез келген
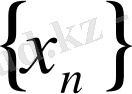 , мұндағы
, мұндағы
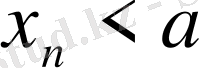 ,
,
 , тізбегіне ƒ функция мәндерінің сәйкес
, тізбегіне ƒ функция мәндерінің сәйкес
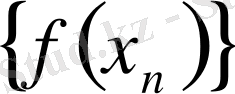 тізбегі
тізбегі
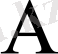 санына жинақталатын болса, онда
санына жинақталатын болса, онда
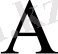 саны
саны
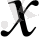 -тің
а
-ға ұмтылғандағы ƒ функциясының сол жақты шегі деп аталады және былай жазылады:
-тің
а
-ға ұмтылғандағы ƒ функциясының сол жақты шегі деп аталады және былай жазылады:
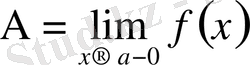
(символдар арқылы:
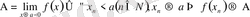 ) .
) .
2
-
анықтама.
Егер кез келген
 үшін оған тәуелді
үшін оған тәуелді
 саны табылып,
саны табылып,
 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық
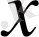 үшін
үшін
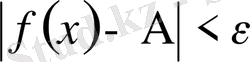 теңсіздігі орындалса, онда A саны x-тің
а
-ға ұмтылғандағы ƒ функциясының сол жақ шегі деп аталады және былай жазылады:
теңсіздігі орындалса, онда A саны x-тің
а
-ға ұмтылғандағы ƒ функциясының сол жақ шегі деп аталады және былай жазылады:
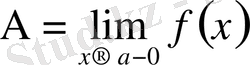 (символдар арқылы:
(символдар арқылы:
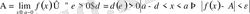 ) .
) .
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz