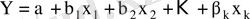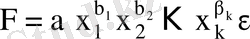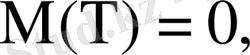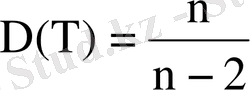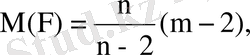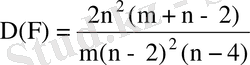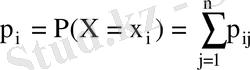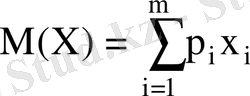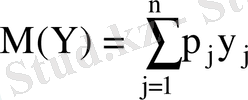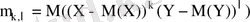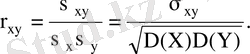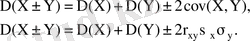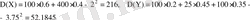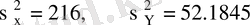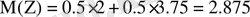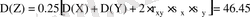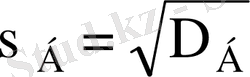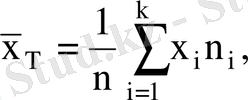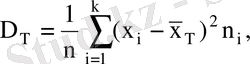Эконометрика: экономика мамандықтары үшін оқу-әдістемелік құрал


Қазақстан Республикасының білім және ғылым министрлігі
С. Торайғыров атындағы Павлодар мемлекеттік университеті
Н. М. Исмағұлова, Т. М. Бергузинова
ЭКОНОМЕТРИКА
Экономика мамандықтарына арналған
оқу - әдістемелік құрал
Павлодар
УДК 519. 862. 6 (075. 8)
ББК 6586я73
Б 44
С. Торайғыров атындағы ПМУ ғылыми кеңесі ұсынған
Пікір білдірушілер:
М. М. Аяшинов − Иновациялық Еуразия университетінің математика кафедрасының меңгерушісі, физика-математика ғылымдарының кандидаты, профессор.
Р. А. Хисматуллин − экономика ғылымдарының кандидаты, профессор.
Т. С. Сабыров − физика-математика ғылымдарының кандидаты, профессор.
Б44 Н. М. Исмағұлова, Т. М. Бергузинова
Эконометрика: оқу - әдістемелік құрал. − Павлодар, 2007. - 95 б.
ISBN 9965-583-15-3
Эконометрика пәні бойынша оқу- әдістемелік құралында ықтималдықтар теориясы, математикалық статистика элементтері, регрессиялық талдау және экономикалық мамандықтарға арналған есептер беріледі. Оқу - әдістемелік құрал экономикалық мамандықтарда оқитын студенттерге арналған.
ISBN 9965-583-15-3 УДК 519. 862. (075. 8)
ББК 6586я73
© Н. М. Исмағұлова, Т. М. . Бергузинова, 2007
© С. Торайғыров атындағы Павлодар
мемлекеттік университеті, 2007
Алғы сөз
Эконометрика қазіргі заманғы экономикалық білім берудегі негізгі пәндердің бірі. Нақты экономикалық құбылыстарды сандық талдау экономикалық зерттеулердің алдыңғы қатарлы әдістерінің негізін құрайды. Экономикалық құбылыстарды сандық талдау экономистер зерттеулерінде қолданылатын алдыңғы қатарлы әдістер негіздерін, экономикалық қатынастар құрылымын, нарық экономикасының талабына сай ұлттық есептер жүйесінің болуын, сол сияқты экономикалық моделдеуді статистикалық қамтамасыз ету қажеттіліктерін қамтитындықтан, «Эконометрика» пәнін жоғары оқу орындарының оқу бағдарламасына енгізу және ғылыми зерттеулерде эконометрикалық әдістерді қолдану маңызды болып табылады. Ұсынылып отырған оқу-әдістемелік құрал С. Торайғыров атындағы Павлодар мемлекеттік университетінің аға оқытушылары Н. М. Исмағұлова мен Т. М. Бергузинованың бірнеше жыл қатарынан аталған университеттің экономикалық мамандықтарының студенттеріне оқылған дәрістер курсы негізінде жазылған.
Аталған оқу - әдістемелік құралы эконометрика пәні бойынша оқулықтар тапшылығына байланысты экономикалық мамандықтарда оқитын студенттерге эконометрикалық әдістер мен моделдер курсын қайталауға мүмкіншілік жасайды.
1 Эконометрикалық моделдер
1. 1 Эконометрика пәні және оның міндеттері
Эконометрика жеке ғылыми пән ретінде пайда болу тарихы 100 жыл шамасында есептеледі. Норвег ғалымы Р. Фриш осы пәнді экономикалық теория, статистика және математика пәндерінің бірігуі деп анықтады. Экономикадағы білімдер экономикалық көрсеткіштер арасындағы байланысты орнатады және экономикалық теория, моделдер түрінде беріледі. Макро және микроэкономикалық теориялардың сапалы (сапа жөніндегі) сұрақтарына жауап береді.
Экономикада ақша ұсынысының артуы пайыздың нақты ставкасына және іскерлік белсенділігіне әсер ете ме? Тұтыну құрылымын салық ставкасының кемуі қалай өзгертеді? Мемлекеттік бюджеттің дефициті инфляция және төлемділік балансының жағдайына қалай әсер етеді?
Аталған сұрақтардың әрқайсысына экономистер теорияға сүйеніп өз пікірлерін айтады. Сонымен қатар, негізделген шешім қабылдау үшін айтылған теориялық заңдылықтарды нақты сандық өрнектеу қажет.
Экономикада алуан ішкі және сыртқы байланыстарды бөліп және жекелеп сипаттау мүмкін емес. Экономикада пайда болатын осындай экономикалық айнымалылар арасындағы тәуелділіктерді тек қана нақты статистикалық мәліметтерді өңдеу аркылы алуға болады.
Сонымен, эконометрика дегеніміз экономикалық теория, статистика және математика ғылымдарына сүйеніп экономикалық құбылыстар мен процестерді сандық өрнектеу.
Эконометриканың негізгі міндеттері:
− құрылған экономикалық моделді эмпирикалық талдау жүргізу
үшін математикалық түрге келтіру, яғни моделді спецификациялау;
− құрылған модель нақты мәліметтерге адекват болу үшін оның параметрлерін бағалау, яғни моделді параметрлеу;
− құрылған моделдің параметрлерінің сапасын және моделдің сапасын тексеру, яғни моделді верификациялау;
− құрылған моделді зерттелініп отырған экономикалық көрсеткіштердің өзгерісін анықтауға, экономикалық құбылыстарды болжауға, экономикалық саясатты дұрыс жүргізу үшін пайдалану.
1. 2 Моделдер
Экономикадағы заңдылықтар экономикалық көрсеткіштердің арасындағы байланыстар түрінде айқындалады. Тауардың тұтынуын зерттеу оның y көлемі, p тауардың бағасына,
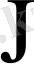 кірістің деңгейіне,
кірістің деңгейіне,
 алмастырушы тауардың бағасына және
алмастырушы тауардың бағасына және
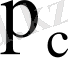 қосымша тауардың бағасына байланысты
қосымша тауардың бағасына байланысты
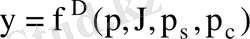
Өндірістік функция экономикадағы Q - өнімінің L еңбек шығынына және K капиталға тәуелділігін анықтайды.
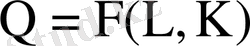
Осындай қатынастар айнымалылардың өзара байланыстары қандай болатынын көрсететін модель болып табылады. Жалпы бір айнымалы
 және n түсіндіруші айнымалылардан құрылған экономикалық модель
және n түсіндіруші айнымалылардан құрылған экономикалық модель
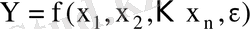
түрінде жазылады, мұнда
 тәуелді айнымалының нақты мәнінің теориялық моделмен анықталған мәнінен ауытқуын түсіндіруге арналған кездейсоқ шама.
тәуелді айнымалының нақты мәнінің теориялық моделмен анықталған мәнінен ауытқуын түсіндіруге арналған кездейсоқ шама.
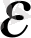 шамасы моделге кірмейтін басқа факторлардың шамасын анықтайды. Моделдер әртүрлі функционалдық түрде болуы мүмкін. Сызықтық экономикалық модель жиі кездеседі.
шамасы моделге кірмейтін басқа факторлардың шамасын анықтайды. Моделдер әртүрлі функционалдық түрде болуы мүмкін. Сызықтық экономикалық модель жиі кездеседі.
Сондай - ақ
дәрежелік экономикалық модель. Мұнда
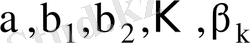 статистикалық мәліметтердің негізінде бағаланатын моделдің параметрлері. Сызықтық және дәрежелік тәуелділіктерден басқа квадраттық, кубтық, логарифмдік, логистік және басқа функциялар қолданылады.
статистикалық мәліметтердің негізінде бағаланатын моделдің параметрлері. Сызықтық және дәрежелік тәуелділіктерден басқа квадраттық, кубтық, логарифмдік, логистік және басқа функциялар қолданылады.
Жалпы эконометрикалық модель:
;
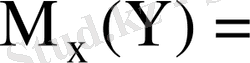
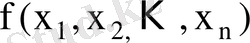
регрессия теңдеуі.
Функционалдық тәуелділіктің түрін таңдау моделдің спецификасы, ал түсіндіруші айнымалылардың құрамын анықтау айнымалылардың спецификасы деп аталады. Егер моделдің тек қана бір түсіндіруші айнымалысы болса, яғни к = 1, онда ол қос регрессия деп аталады. Егер к > 1 болса, онда регрессия жиындық болады. Эконометрикалық моделдің негізін статистикалық мәліметтер құрайды.
2 Ықтималдықтар теориясы
2. 1 Оқиғалар. Оқиғаның ықтималдығы
 оқиғасының ықтималдығы
оқиғасының ықтималдығы
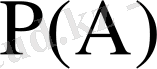 деп осы оқиғаның пайда болу мүмкіндігінің сандық өлшемін атайды.
деп осы оқиғаның пайда болу мүмкіндігінің сандық өлшемін атайды.
Анықтама
 оқиғасының ықтималдығы
оқиғасының ықтималдығы
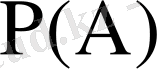 деп осы оқиғаның пайда болуына қолайлы оқиғалар (тәжірибелер)
деп осы оқиғаның пайда болуына қолайлы оқиғалар (тәжірибелер)
 санының барлық элементар оқиғалар (тәжірибелер)
санының барлық элементар оқиғалар (тәжірибелер)
 санына қатынасын атайды
санына қатынасын атайды
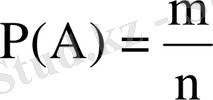 (1)
(1)
Ақиқат оқиға деп тәжірибе нәтижесінде міндетті түрде пайда болатын оқиғаны атайды.
Мүмкін емес оқиға деп тәжірибе нәтижесінде пайда болмайтын оқиғаны атайды.
Кездейсоқ оқиға деп тәжірибе нәтижесінде пайда болуы да, болмауы да мүмкін оқиғаны атайды.
Бір уақытта пайда болуы мүмкін емес оқиғалар үйлесімсіз оқиғалар деп аталады.
Ықтималдықтың қасиеттері:
1)
;
2) ақиқат оқиға
ның ықтималдығы бірге тең:
;
3) мүмкін емес оқиға
ның ықтималдығы нөлге тең:
;
4) егер
 және
және
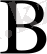 үйлесімсіз оқиғалар болса, онда
үйлесімсіз оқиғалар болса, онда
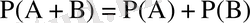 ;
;
5) егер
 және
және
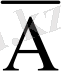 қарама қарсы оқиғалар болса, онда
қарама қарсы оқиғалар болса, онда
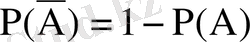 .
.
2. 2 Кездейсоқ шама
Кездейсоқ шама деп, өзінің мүмкін мәндер жиыиынан бақылау нәтижесінде алдын-ала белгісіз және кездейсоқ жағдайларға тәуелді бір ғана мән қабылдайтын шаманы атайды. Кездейсоқ шамалар дискретті және үздіксіз болып екіге бөлінеді. Дискретті кездейсоқ шама
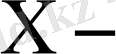 тің үлестіру заңы кестемен берілсе, онда бірінші жол
тің үлестіру заңы кестемен берілсе, онда бірінші жол
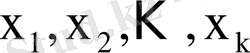 оның мүмкін мәндері, ал екінші жол сәйкес ықтималдықтары
оның мүмкін мәндері, ал екінші жол сәйкес ықтималдықтары
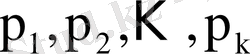 болады.
болады.

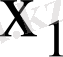

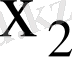

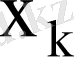

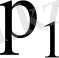


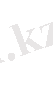
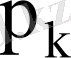
Әдетте
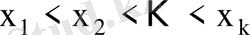 . Міндетті түрде
. Міндетті түрде
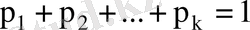
Мысал 1


Айталық
 - кездейсоқ шама, ал
- кездейсоқ шама, ал
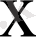 -кез келген нақты сан. Кез келген
-кез келген нақты сан. Кез келген
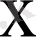 -тен кіші мән қабылдайтын
-тен кіші мән қабылдайтын
 - кездейсоқ шаманың ықтималдығын ықтималдықтың
- кездейсоқ шаманың ықтималдығын ықтималдықтың
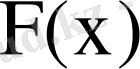 үлестіру функциясы деп атайды.
үлестіру функциясы деп атайды.
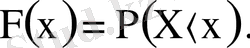 (2)
(2)
Үлестіру функциясының қасиеттері:
1)
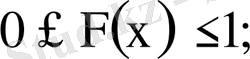
2)
 кемімейтін функция, яғни
кемімейтін функция, яғни
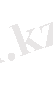
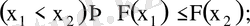
3)
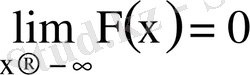 ,
,

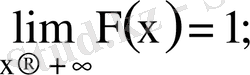
4)
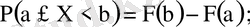
5)
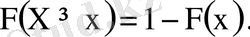
6)
 кездейсоқ шаманың мүмкін мәндері
кездейсоқ шаманың мүмкін мәндері
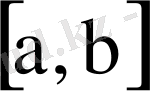 аралығында жататын болса, онда
аралығында жататын болса, онда
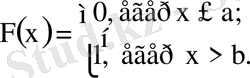
1 мысал үшін үлестіру функциясы және оның графигі
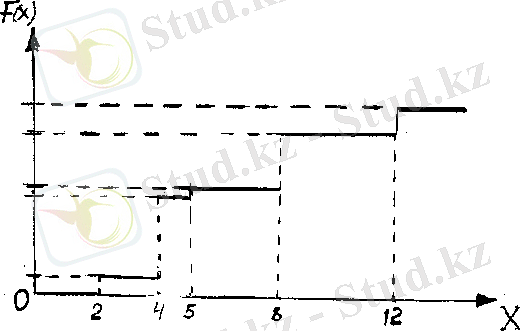
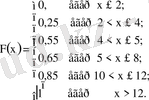
Сурет 1
Үздіксіз кездейсоқ шама X- тің ықтималдық тығыздығы деп сол шаманың үлестіру функциясының бірінші ретті туындысын атайды, яғни
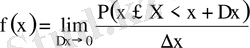 (3)
(3)
функциясын атайды.
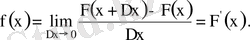 (4)
(4)
Ықтималдық тығыздығының қасиеттері:
1)
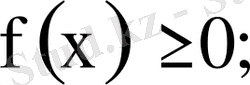
2)
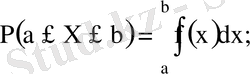
3) Егер
 үздіксіз кездейсоқ шаманың үлестіру тығыздығы болса, онда үлестіру функциясы
үздіксіз кездейсоқ шаманың үлестіру тығыздығы болса, онда үлестіру функциясы
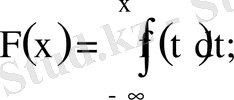
4)
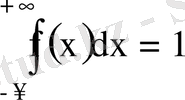 (нормалау шарты) .
(нормалау шарты) .
Үздіксіз кездейсоқ шама үшін келесі теңдіктер орындалады.
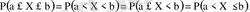
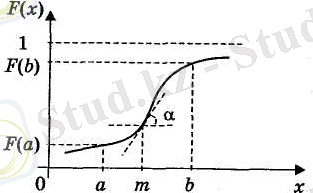
2 және 3 суреттерде үздіксіз кездейсоқ шаманың үлестіру функциясы және ықтималдық тығыздығы бейнеленген.
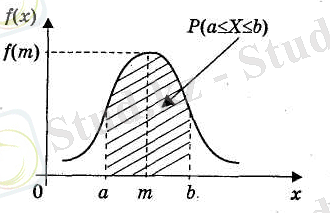
Сурет 2 Сурет 3
2. 3 Кездейсоқ шаманың сандық сипаттамалары
Дискретті кездейсоқ шаманың математикалық үміті деп оның барлық мүмкін мәндерінің сәйкес ықтималдықтарына көбейтіндісінің қосындысын атайды.
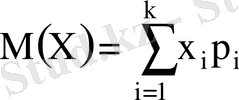 , (5)
, (5)
мұнда
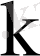 - кездейсоқ шама
- кездейсоқ шама
 -тің мәндерінің саны.
-тің мәндерінің саны.
Үздіксіз кездейсоқ шама үшін
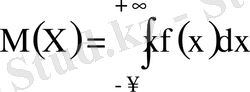 . (6)
. (6)
1 мысалдағы кездейсоқ шама үшін
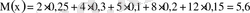 .
.
Математикалық үміттің қасиеттері:
1)
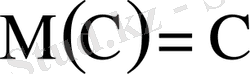 , мұнда С- тұрақты шама;
, мұнда С- тұрақты шама;
2)
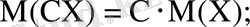
3)
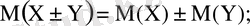
4)
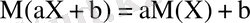 , мұнда
, мұнда
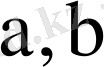 - тұрақты шамалар;
- тұрақты шамалар;
5) Тәуелсіз кездейсоқ шамалар үшін
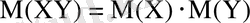 .
.
 кездейсоқ шаманың
кездейсоқ шаманың
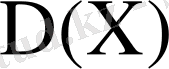 дисперсиясы деп кездейсоқ шаманың математикалық үміттен ауытқуының квадратының математикалық үмітін атайды.
дисперсиясы деп кездейсоқ шаманың математикалық үміттен ауытқуының квадратының математикалық үмітін атайды.
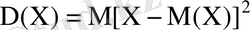
Ықшамдалған формула
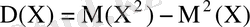 .
(7)
.
(7)
Дискретті кездейсоқ шама үшін
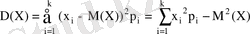 . (8)
. (8)
Үздіксіз кездейсоқ шама үшін
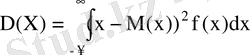 (9)
(9)
1 мысалдағы кездейсоқ шама үшін
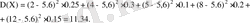
Дисперсияның қасиеттері:
1)
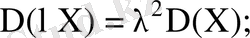
2)
тәуелсіз кездейсоқ шамалар болса,
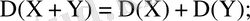
3)
Equation. 3
4)
Equation. 3 кез келген кездейсоқ шамалар болса,
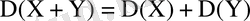
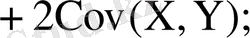
Орташа квадраттық (сандартты) ауытқу деп, дисперсияның квадрат түбірінің арифметикалық мәнін атайды және былай белгілейді
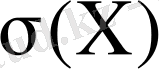
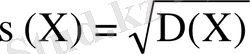 (10)
(10)
2. 4 Кездейсоқ шамалардың үлестіру заңдары
Көптеген кездейсоқ шамалардың үлестіру заңдарын білу арқылы олардың анықталған интервалда мән қабылдау ықтималдығын болжауға болады. Үлестіру заңдары өте көп. Біз тек қана экономикалық талдауда жиі кездесетін үлестіру заңдарын қарастырамыз. Оларға жататын: қалыпты үлестіру заңы,
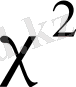 (хи - квадрат), Стьюдент, Фишер үлестірулері.
(хи - квадрат), Стьюдент, Фишер үлестірулері.
Қалыпты үлестіру. Үлестіру тығыздығы
(11)
түрінде берілген кездейсоқ шама
 қалыпты үлестірілген кездейсоқ шама деп аталады. Қалыпты үлестірудің үлестіру функциясы
қалыпты үлестірілген кездейсоқ шама деп аталады. Қалыпты үлестірудің үлестіру функциясы
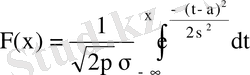 (12)
(12)
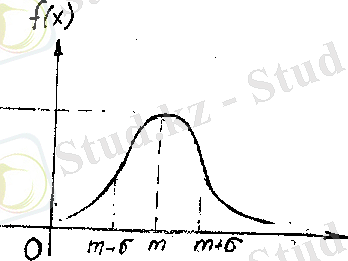 Қалыпты үлестірілген кездейсоқ шаманың тығыздығы және үлестіру функциясының графиктері 4 және 5 суреттерде көрсетілген.
Қалыпты үлестірілген кездейсоқ шаманың тығыздығы және үлестіру функциясының графиктері 4 және 5 суреттерде көрсетілген.
Сурет 4
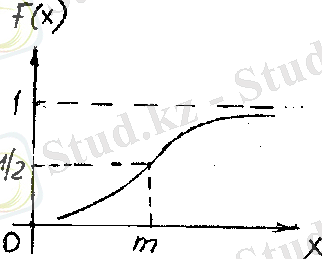
Сурет 5
(11) және (12) формулаларынан қалыпты үлестіру
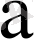 және σ параметрлерімен анықталады және олардан тәуелді
және σ параметрлерімен анықталады және олардан тәуелді
Егер
 қалыпты үлестірілген кездейсоқ шама
қалыпты үлестірілген кездейсоқ шама
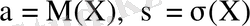 болса, онда келесі символмен
болса, онда келесі символмен
 ~
~
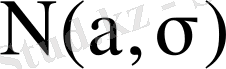 ,
,
 ~
~
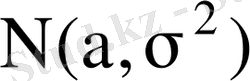 деп жазуға болады. Қалыпты үлестірудің маңызды дербес жағдайы
деп жазуға болады. Қалыпты үлестірудің маңызды дербес жағдайы
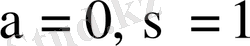 , стандартты қалыпты үлестіру деп аталады. Стандартты қалыпты үлестірілген кездейсоқ шама
, стандартты қалыпты үлестіру деп аталады. Стандартты қалыпты үлестірілген кездейсоқ шама
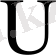 ~
~
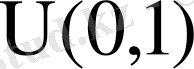 деп белгіленеді.
деп белгіленеді.
(13)
Көп жағдайда практикалық есептеулерде мәндері кестемен берілген Лаплас функциясы қолданылады.
(14)
Бұл кестені кез келген қалыпты үлестірілген кездейсоқ шамалар
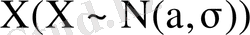 үшін келесі ықтималдықтарды есептеуге пайдалануға болады
үшін келесі ықтималдықтарды есептеуге пайдалануға болады
(15)
Егер
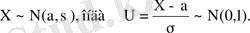
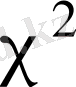 (хи - квадрат) үлестіруі.
(хи - квадрат) үлестіруі.
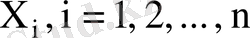 - тәуелсіз қалыпты үлестірілген кездейсоқ шамалар.
- тәуелсіз қалыпты үлестірілген кездейсоқ шамалар.
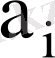 және
және
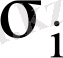 сәйкесінше математикалық үміттер, орташа квадраттық ауытқулар, яғни
сәйкесінше математикалық үміттер, орташа квадраттық ауытқулар, яғни
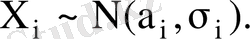 Онда
Онда
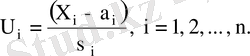 , тәуелсіз қалыпты үлестірілген стандартты кездейсоқ шамалар болады,
, тәуелсіз қалыпты үлестірілген стандартты кездейсоқ шамалар болады,
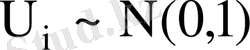 . Кездейсоқ шама
. Кездейсоқ шама
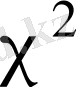 ,
n еркіндік дәрежелі хи - квадрат үлестіруі
,
n еркіндік дәрежелі хи - квадрат үлестіруі
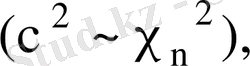 болады, егер
болады, егер
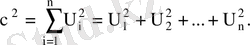 (16)
(16)
Еркіндік дәрежесін
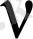 деп белгілейміз,
деп белгілейміз,
 қосындылар құрамына кіретін кездейсоқ шамалар саны, ал
қосындылар құрамына кіретін кездейсоқ шамалар саны, ал
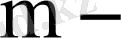 кездейсоқ шамаларды байланыстыратын сызықтық теңдеулер саны.
кездейсоқ шамаларды байланыстыратын сызықтық теңдеулер саны.
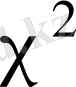 (
хи - квадрат) кездейсоқ шаманың еркіндік дәрежесі
(
хи - квадрат) кездейсоқ шаманың еркіндік дәрежесі
 санымен анықталады. Олай болса,
санымен анықталады. Олай болса,
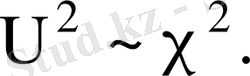 Хи - квадрат үлестіруінің математикалық үміті және дисперсиясы:
Хи - квадрат үлестіруінің математикалық үміті және дисперсиясы:
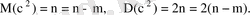
Егер
 және
және
 тәуелсіз
тәуелсіз
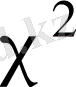 үлестірілген еркіндік дәрежелері
үлестірілген еркіндік дәрежелері
 және
және
 кездейсоқ шамалар болса
кездейсоқ шамалар болса
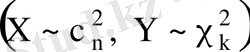 , онда олардың қосындысы да
, онда олардың қосындысы да
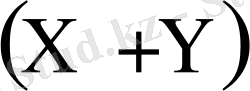 еркіндік дәрежесі
еркіндік дәрежесі
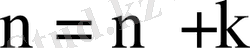 -ға тең
-ға тең
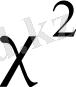 үлестірілген кездейсоқ шама болады.
үлестірілген кездейсоқ шама болады.
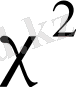 үлестіруі статистикалық болжамдарды тексеруде интервалдық бағаларды табу үшін қолданылады.
үлестіруі статистикалық болжамдарды тексеруде интервалдық бағаларды табу үшін қолданылады.
Стьюдент үлестіруі.
Айталық
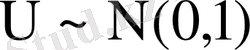 кездейсоқ шама, ал V- еркіндік дәрежесі
кездейсоқ шама, ал V- еркіндік дәрежесі
 ,
,
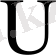 - дан тәуелсіз
- дан тәуелсіз
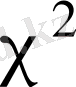 үлестірілген кездейсоқ шама болсын. Онда
үлестірілген кездейсоқ шама болсын. Онда
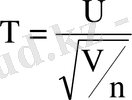 (17)
(17)
 Equation. 3 еркіндік дәрежелі Стьюдент үлестіруі (
Equation. 3 еркіндік дәрежелі Стьюдент үлестіруі (
 -үлестіруі ) деп аталады, яғни (
-үлестіруі ) деп аталады, яғни (
 ~
~
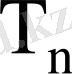 ) . (17) формуладан Стьюдент үлестіруі тек қана бір параметр, яғни
) . (17) формуладан Стьюдент үлестіруі тек қана бір параметр, яғни
 еркіндік дәрежесімен анықталатынын көруге болады. Стьюдент үлестіруінің математикалық үміті және дисперсиясы:
еркіндік дәрежесімен анықталатынын көруге болады. Стьюдент үлестіруінің математикалық үміті және дисперсиясы:
Фишер үлестіруі.
 Equation. 3 еркіндік дәрежелері
Equation. 3 еркіндік дәрежелері
 және
және
 Equation. 3 тәуелсіз
Equation. 3 тәуелсіз
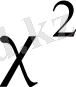 үлестірілген кездейсоқ шамалар болса, онда шама
үлестірілген кездейсоқ шамалар болса, онда шама
(18)
еркіндік дәрежелері
 және
және
 Фишер үлестіруі деп аталады. Олай болса,
Фишер үлестіруі деп аталады. Олай болса,
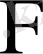 Фишер үлестіруі екі параметрмен анықталады, яғни
Фишер үлестіруі екі параметрмен анықталады, яғни
 және
және
 еркіндік дәрежелерімен. Стьюдент үлестіруінің математикалық үміті және дисперсиясы:
еркіндік дәрежелерімен. Стьюдент үлестіруінің математикалық үміті және дисперсиясы:
 және
және
 нің үлкен мәндерінде Фишер үлестіруі қалыпты үлестіруге ұқсайды. Фишер үлестіруі дисперсиялық және регрессиялық талдауда статистикалық болжамдарды тексеруге пайдаланылады.
нің үлкен мәндерінде Фишер үлестіруі қалыпты үлестіруге ұқсайды. Фишер үлестіруі дисперсиялық және регрессиялық талдауда статистикалық болжамдарды тексеруге пайдаланылады.
2. 5 Кездейсоқ шамалардың өзара байланысы
Көптеген экономикалық көрсеткіштер бірнеше сандармен анықталады, яғни көпөлшемді кездейсоқ шамалар болып табылады. Экономикалық көрсеткіштердің бірқатар мәндері басқа көрсеткіштердің мәндерін анықтайды.
Сондықтан экономикалық талдаудың басты міндеттерінің бірі- экономикалық көрсеткіштерді анықтау және олардың арасындағы байланысты көрсету. (нақты кездейсоқ шамалар арасында) .
Мысалы: кіріс пен тұтыну арасындағы; тауар сұранымы және тауар бағасы арасындағы; инфляция деңгейі және жұмыссыздық деңгейі арасындағы; жалпы ұлттық өнім және тіршілік деңгейі арасындағы байланыстар.
Дербес жағдайда екі кездейсоқ шама арасындағы тәуелділікті орнату үшін екіөлшемді ықтималдықтар қарастырылады.
 және
және
 кездейсоқ шамалары дискретті үлестіру кестесімен берілсе
кездейсоқ шамалары дискретті үлестіру кестесімен берілсе


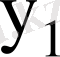
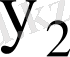

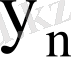
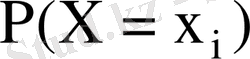
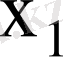
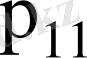
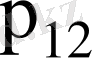

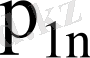
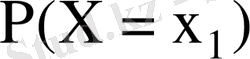
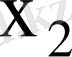
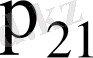


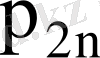
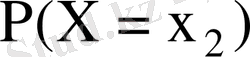






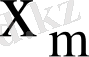
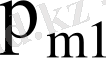
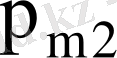

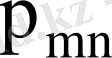
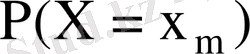
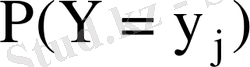
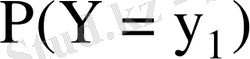
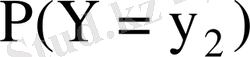

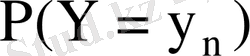
Мұнда
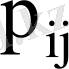 - бір уақытта
- бір уақытта
 кездейсоқ шама
кездейсоқ шама
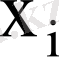 , ал
, ал
 кездейсоқ шама
кездейсоқ шама
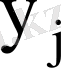 мәндерін қабылдау ықтималдығы, яғни
мәндерін қабылдау ықтималдығы, яғни
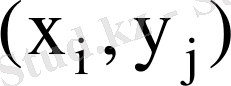 қос мәнінің пайда болу ықтималдығы
қос мәнінің пайда болу ықтималдығы
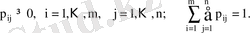
 тің кез келген мәнінде
тің кез келген мәнінде
 мән қабылдау ықтималдығы
мән қабылдау ықтималдығы
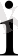 жатық жолының ықтималдықтарының қосындысына тең
жатық жолының ықтималдықтарының қосындысына тең
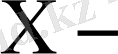 тің кез-келген мәнінде
тің кез-келген мәнінде
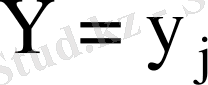 мән қабылдау ықтималдығы
мән қабылдау ықтималдығы
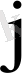 тік жолының ықтималдықтарының қосындысына тең
тік жолының ықтималдықтарының қосындысына тең
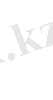
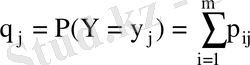
 және
және
 кездейсоқ шамаларының сәйкесінше математикалық үміттері:
кездейсоқ шамаларының сәйкесінше математикалық үміттері:
Сол сияқты
 және
және
 кездейсоқ шамаларының дисперсиялары:
кездейсоқ шамаларының дисперсиялары:
Үздіксіз екіөлшемді кездейсоқ шаманың үлестіру функциясы және ықтималдықтар тығыздығы:
Біріккен үлестіру функциясы
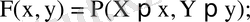
Біріккен ықтималдық тығыздығы
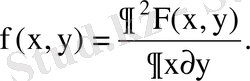
Тәуелсіз кездейсоқ шамалар
Егер
және
кездейсоқ шамалары үшін
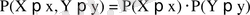
теңдігі орындалса, онда мұндай кездейсоқ шамаларды тәуелсіз деп атайды. Тәуелсіз
 және
және
 кездейсоқ шамалары үшін келесі қатынастардың кез келгені орындалады.
кездейсоқ шамалары үшін келесі қатынастардың кез келгені орындалады.
Ковариация және корреляция коэффициенті.
Кездейсоқ шамалардың өзара байланысын талдауда ковариация және корреляция коэффициенті қолданылады.
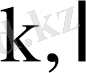 ретті орталық момент деп
ретті орталық момент деп
шамасын атайды.
 және
және
 кездейсоқ шамаларының байланысын анықтау үшін
кездейсоқ шамаларының байланысын анықтау үшін
 және
және
 кездейсоқ шамаларының ковариациясы деп аталатын
кездейсоқ шамаларының ковариациясы деп аталатын
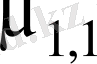 орталық моментін қолданамыз.
орталық моментін қолданамыз.
Ковариация
 және
және
 кездейсоқ шамаларының байланысының абсолюттік өлшемі болады. Дискретті кездейсоқ щама үшін
кездейсоқ шамаларының байланысының абсолюттік өлшемі болады. Дискретті кездейсоқ щама үшін
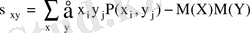
Үздіксіз кездейсоқ шама үшін
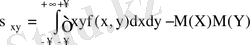
Ковариацияның қасиеттері:
1)

2)
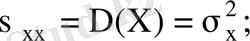
3) егер
және
тәуелсіз кездейсоқ шамалар болса, онда
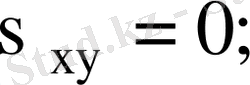
4)
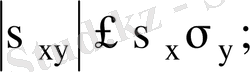
5)
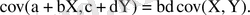
 және
және
 кездейсоқ шамаларының корреляция коэффициенті деп келесі формуламен анықталатын шаманы атайды
кездейсоқ шамаларының корреляция коэффициенті деп келесі формуламен анықталатын шаманы атайды
Егер
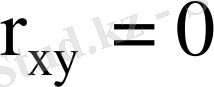 болса, онда
болса, онда
 және
және
 кездейсоқ шамаларының арасында корреляциялық байланыс жоқ, ал егер
кездейсоқ шамаларының арасында корреляциялық байланыс жоқ, ал егер
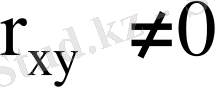 болса, корреляциялық байланыс бар.
болса, корреляциялық байланыс бар.
Корреляция коэффициентінің қасиеттері:
1)

2)

3)
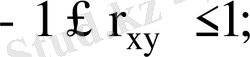
4) егер
 және
және
 кездейсоқ шамалары тәуелсіз болса, онда
кездейсоқ шамалары тәуелсіз болса, онда
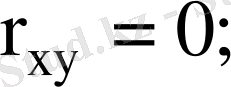
5) егер
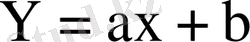 болса,
болса,
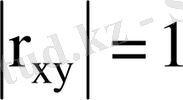 (яғни
(яғни
 және
және
 кездейсоқ шамаларының арасында сызықтық тәуелділік бар) . Егер
кездейсоқ шамаларының арасында сызықтық тәуелділік бар) . Егер
 және
және
 кездейсоқ шамалары тәуелді болса, онда
кездейсоқ шамалары тәуелді болса, онда
Мысал 2
Көп жылдар бойы екі компанияға салынған инвестиция нәтижелерін бақылау бойынша
 және
және
 - жылдық дивидендтер өлшемдерінің үлестіру заңы құрылған. Әр кездейсоқ шаманың маргиналды үлестіру заңын жазып, олардың арасындағы байланысты анықтаңыздар. Ковариация және корреляция коэффициенттерін есептеңіз, екі компанияның біреуіне немесе екеуіне де бірдей мөлшерде инвестиция салу тәуекелін есептеп, тиімді жағдайды анықтаңыз.
- жылдық дивидендтер өлшемдерінің үлестіру заңы құрылған. Әр кездейсоқ шаманың маргиналды үлестіру заңын жазып, олардың арасындағы байланысты анықтаңыздар. Ковариация және корреляция коэффициенттерін есептеңіз, екі компанияның біреуіне немесе екеуіне де бірдей мөлшерде инвестиция салу тәуекелін есептеп, тиімді жағдайды анықтаңыз.
Y
X
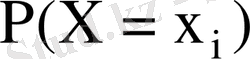
20
20
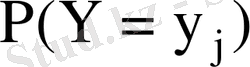
 және
және
 кездейсоқ шамаларының үлестіру заңдары
кездейсоқ шамаларының үлестіру заңдары
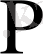
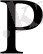

,
ендеше
 және
және
 кездейсоқ шамалары тәуелді.
кездейсоқ шамалары тәуелді.
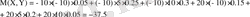
 және
және
 кездейсоқ шамалары арасындағы байланыс ковариациямен анықталады.
кездейсоқ шамалары арасындағы байланыс ковариациямен анықталады.
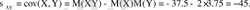
.
 және
және
 кездейсоқ шамаларының арасында теріс тығыз емес сызықтық байланыс бар деп айтуға болады. Инвестиция тәуекелін дивидендтер мәнінің шашылуына байланысты кездейсоқ шамалардың дисперсиялары бойынша есептеуге болады.
кездейсоқ шамаларының арасында теріс тығыз емес сызықтық байланыс бар деп айтуға болады. Инвестиция тәуекелін дивидендтер мәнінің шашылуына байланысты кездейсоқ шамалардың дисперсиялары бойынша есептеуге болады.
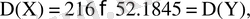
олай болса бірінші компанияға инвестиция салу екінші компанияға қарағанда тиімді емес.
 деп, екі компанияға бірден бірдей мөлшерде инвестиция салуда дивидендтер өлшемін белгілейік. Ендеше
деп, екі компанияға бірден бірдей мөлшерде инвестиция салуда дивидендтер өлшемін белгілейік. Ендеше
 .
.
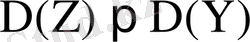 осыдан қарастырылған үш жағдайдан екі компанияға бірден бірдей мөлшерде инвестиция салған тиімді екенін көреміз.
осыдан қарастырылған үш жағдайдан екі компанияға бірден бірдей мөлшерде инвестиция салған тиімді екенін көреміз.
3 Математикалық статистика элементтері
Нақты экономикалық құбылыстарды әртүрлі көрсеткіштер бойынша зерттеуде өте көп статистикалық мәліметтерді өңдеуге тура келеді. Статистикалық мәліметтер құрылымы бойынша кездейсоқ шамалар болып табылады. Көп жағдайда параметрлердің сандық мәндерін бағалау үшін бірнеше рет болжам қоюға және оларды тексеруге тура келеді. Әртүрлі факторлар арасындағы тәуелділікті орнату және тәуелділіктің шамасын анықтау қажет.
Статистикалық мәліметтер дегеніміз жүргізілген байқаулардың, тәжірибелердің қорытындысы. Математикалық статистиканың негізгі міндеттерінің бірі статистикалық мәліметтердің заңдылықтарын айқындап, оларға сәйкес экономикалық модель құру және шешімдер қабылдау. Математикалық статистиканың бірінші міндеті байқаулар, тәжірибелер арқылы алынған мәліметтерді жинастырып, топтастыру әдістерін көрсету. Ал екінші міндеті статистикалық мәліметтерді алға қойған мақсатқа байланысты талдау жасау әдістерін табу.
Бас жиынтық және таңдама. Бас жиынтық деп белгілі қасиеттерімен бірігетін барлық қарастырылып отырған объектілер жиынын атайды. Жеке объект осы жиынның элементі болады. Егер бір кәсіпорынды алатын болсақ, онда жеке жұмысшы объект болады да, ал кәсіпорынның барлық жұмысшылары бас жиынтық болады. Бас жиынтықтағы объектілер саны ақырлы немесе ақырсыз көп сан болуына байланысты бас жиынтық шектелген және шектелмеген болып екіге бөлінеді.
Таңдама дегеніміз бас жиынтықтан кездейсоқ таңдап алынған объектілер жиынтығы. Бас және таңдама жиынтықтағы объектілер саны олардың көлемі деп аталады. Бас жиынтықтың көлемі үлкен болса, түгелдей тексеру мүмкін емес. Егер зерттелініп отырған объектілер жиыны жойылуға жататын (өзіндік құнын жоғалтуына байланысты), немесе практикада өте көп материалдық шығындарды қажет ететін болса, онда толық талдаудың мәні болмайды. Бас жиынтық жөніндегі тұжырым дұрыс болуы үшін бөлініп алынған таңдама бас жиынтық туралы жан-жақты сипаттама беруге тиіс. Экономикалық процестерді болжауда, олардың тиімді шешімін табуда таңдаманы құрудың үлкен мағынасы бар. Таңдаманы құру әдістері:
1) бас жиынтықты ұсақ бөліктерге бөлуді талап етпейтін таңдау: қайталамалы және қайталанбайтын таңдамалар. Бөліп алынған таңдама зерттелініп болғаннан кейін бас жиынтыққа қайта қосылатын болса таңдама қайталамалы, ал қосылмайтын болса таңдама қайталанбайтын деп аталады;
2) бас жиынтықты ұсақ бөліктерге бөлуді талап ететін таңдау: типтік, механикалық, сериялық таңдаулар.
Типтік таңдауда бас жиынтық типтес бөліктерге бөлінеді де, әр бөліктен тәуекелге бір-бірден объект таңдап алынады.
Механикалық таңдауда, бас жиынтық механикалық түрде қанша объекті таңдамаға кіретін болса, сонша бөлікке бөлінеді де, әрбір бөліктен бір-бірден объект таңдап алынып таңдама құрылады.
Бас жиынтық алдын-ала өзара қиылыспайтын бірнеше серияға бөлінеді де, ол сериялардың біреуі кездейсоқ таңдап алынса, онда осы серияның барлық элементтері таңдама жиынтық құрады.
Таңдаманың статистикалық үлестіруі.
Бас жиынтықтан көлемі
 болатын таңдама бөлініп алынды делік. Оларды
болатын таңдама бөлініп алынды делік. Оларды
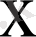 -тің мәндерінің өсу ретіне байланысты
-тің мәндерінің өсу ретіне байланысты
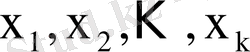 деп жазамыз. Бақылау бойынша
деп жазамыз. Бақылау бойынша
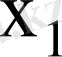 элементі
элементі
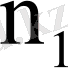 рет,
рет,
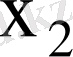 элементі
элементі
 рет, тағы сол сияқты
рет, тағы сол сияқты
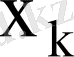 элементі
элементі
 рет пайда болсын, мұндағы
рет пайда болсын, мұндағы
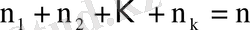 , онда тәжірибелер нәтижесінде алынған
, онда тәжірибелер нәтижесінде алынған
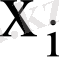 - варианталар, ал
- варианталар, ал
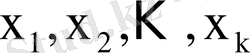 тізбегі вариациялық қатар деп аталады.
тізбегі вариациялық қатар деп аталады.
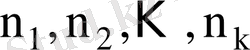 - сәйкес варианталардың жиіліктері,
- сәйкес варианталардың жиіліктері,
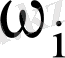 - варианталардың салыстырмалы жиіліктері, мұндағы
- варианталардың салыстырмалы жиіліктері, мұндағы
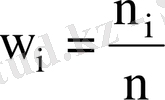 ,
,
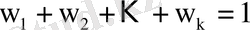 .
.
Таңдаманың статистикалық үлестіруі деп варианталар мен, олардың жиіліктерінің немесе салыстырмалы жиіліктерінің арасындағы өзара бір мәнді сәйкестікті атайды. Таңдаманың құлашы деп, оның ең үлкен және ең кіші варианталарының айырымын айтады. Вариациялық қатар дискретті және үздіксіз болып екіге бөлінеді. Вариациялық қатар дискретті деп аталады, егер шаманың мәндері бір бірінен кемінде кейбір тұрақты санға өзеше болса. Егер шама интервалдар тізбегімен және оларға сәйкес жиіліктерімен берілетін болса (интервал жиілігі осы интервалға кіретін варианталардың жиіліктерінің қосындысы), онда вариациялық қатар үздіксіз деп аталады.

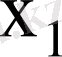
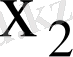

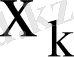
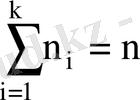
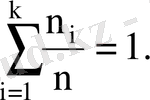
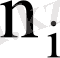
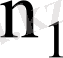



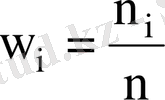
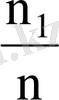
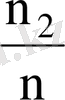

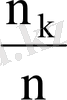
Статистиклық қатар бойынша эмпирикалық үлестіру функциясын құруға болады.
Эмпирикалық үлестіру функциясы.
Эмпирикалық үлестіру функциясы деп әрбір
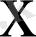 -тің мәні үшін
-тің мәні үшін
 оқиғасының салыстырмалы жиілігін атайды.
оқиғасының салыстырмалы жиілігін атайды.
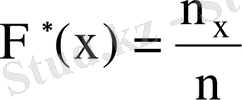 ,
,
мұндағы
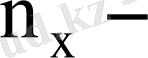 кездейсоқ шама
кездейсоқ шама
 жиілігі,
жиілігі,
 таңдама көлемі. Анықтама бойынша
таңдама көлемі. Анықтама бойынша
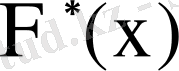 функциясының қасиеттері:
функциясының қасиеттері:
1)
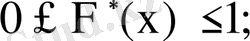
2) кез келген
үшін
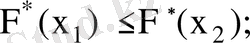
3)
егер
болса,
егер
болса.
Таңдаманың сандық сипаттамалары.
 көлемі N саны болатын бас жиынтық болсын.
көлемі N саны болатын бас жиынтық болсын.
Анықтама 1
Бас орта деп бас жиынтық обьектілерінің арифметикалық ортасын атайды және
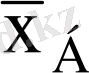 деп белгілейді
деп белгілейді
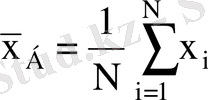
Анықтама 2
Бас дисперсия деп бас жиынтық қабылдайтын барлық мүмкін мәндерінің бас ортасынан ауытқуының квадратының арифметикалық ортасын атайды және
 деп белгілейді
деп белгілейді
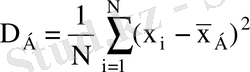
Анықтама 3
Бас дисперсияның квадрат түбірі бас орташа квадраттық ауытқу деп аталады.
 - көлемі n саны болатын таңдама жиынтық болсын. Таңдаманың ортасы, таңдаманың дисперсиясы, таңдаманың орташа квадраттық ауытқуы келесі формулалармен анықталады.
- көлемі n саны болатын таңдама жиынтық болсын. Таңдаманың ортасы, таңдаманың дисперсиясы, таңдаманың орташа квадраттық ауытқуы келесі формулалармен анықталады.
мұнда
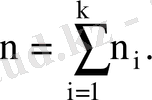
Дисперсияны есептеудің ықшамдалған формуласы
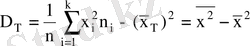
Полигон және гистограмма.
Статистикалық үлестіруді толық түсіну үшін, оларды полигон және гистограммамен көрсетуге болады. Бұл екі ұғымның экономикалық процесстерді зерттеуде үлкен маңызы бар. Полигон жиіліктің және салыстырмалы жиіліктің полигоны болып екіге бөлінеді. Жазықтықта
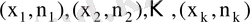 нүктелерін сынық сызықпен қосқанда пайда болған көпбұрыш жиілік полигоны деп аталады. Салыстырмалы жиілік полигоны деп жазықтықта
нүктелерін сынық сызықпен қосқанда пайда болған көпбұрыш жиілік полигоны деп аталады. Салыстырмалы жиілік полигоны деп жазықтықта
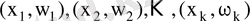 нүктелерін сынық сызықпен қосқанда пайда болатын көпбұрышты атайды. Жиілік гистограммасы деп табандары h, биіктігі
нүктелерін сынық сызықпен қосқанда пайда болатын көпбұрышты атайды. Жиілік гистограммасы деп табандары h, биіктігі
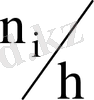 (жиілік тығыздығы) болатын тік төртбұрыштардан тұратын сатылы фигураны атайды. Салыстырмалы жиілік гистограммасы деп табандары h, биіктігі
(жиілік тығыздығы) болатын тік төртбұрыштардан тұратын сатылы фигураны атайды. Салыстырмалы жиілік гистограммасы деп табандары h, биіктігі
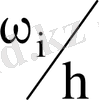 (салыстырмалы жиілік тығыздығы) болатын тік төртбұрыштардан тұратын сатылы фигураны атайды.
(салыстырмалы жиілік тығыздығы) болатын тік төртбұрыштардан тұратын сатылы фигураны атайды.
Мысал 2 Кейбір тауардың 50 күн ішінде күнделікті сатылған көлемі талданып, келесі мәліметтер алынған.
5, 6, 3, 2, 7, 7, 6, 6, 6, 4, 5, 6, 3, 9, 7, 4, 6, 7, 8, 8, 5, 5, 4, 3, 6, 6, 7, 7, 8, 8, 6, 4, 5, 6, 7, 7. 8, 9, 5, 6, 4, 2, 7, 8, 7, 9, 5, 6, 9, 5.
a) статистикалық қатар құрыңыз;
ә) таңдаманың құлашын есептеңіз;
б) эмпирикалық функция құрып, графигін салыңыз;
в) таңдаманың ортасын, дисперсиясын, орташа квадраттық ауытқуын анықтаңыздар.
a) статистикалық қатар
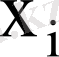
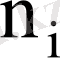
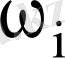
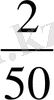
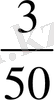
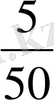
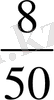
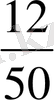
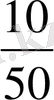
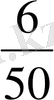
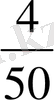
ә) таңдаманың құлашы 9 - 2 = 7
б) эмпирикалық функция

... жалғасыв)
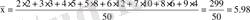

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz