Анықталған интегралдарды жуықтап есептеу: тік бұрыштар әдісін Паскаль тілінде бағдарламалау және қателерді талдау


Астана қаласының көлік және коммуникация колледжі
1 курс студенті:Сыздық Арғын
Ғылыми жетекшісі:Мырзагалиева Гульмира Галиаскаровна
АНЫҚТАЛҒАН ИНТЕГРАЛДЫ ЖУЫҚТАП ШЕШУ. ТІК БҰРЫШТАР ӘДІСІН БАҒДАРЛАМАЛАУ
Дербес ЭЕМ-нің кең таралуы және жер-жерлерде компьютерлік сауаттылықтың дамуы ЭЕМ-де есептеулердің түрліше әдістерінің мақсаты мен механизмін жеңілірек қабылдауға да көмектеседі. Білім беру тәжірибесі көрсеткендей көптеген математикалық емес мамандықтардағы студенттер өздерінің қазіргі және болашақтағы іскерлік жұмыстарында ЭЕМ - ді және де программалау тілдерін, түрлерін, әдістерін қолданып келеді.
Жалпы ЭЕМ - ді қолдана отырып көптеген математикалық есептер шешуге болады. Соның бірі математиканың бір бөлімі анықталған интеграл тақырыбын жуықтап есептеудегі шешімдерді бағдарламалау тілі арқылы табуды қарастырып отырмыз. Бағдарламалау тілі ретінде Паскаль құрылымдық тілін алып отырмыз.
Жазық фигуралардың ауданын жуықтап есептеуде үшбұрыш, төртбұрыш, трапеция, дөңгелек және т. б. жазық фигуралардың ауданын табуға арналған формулалар бар. Және біз бұл білімімізді күнделікті тұрмысымызда пайдаланып та жүрміз. Алайда өмірде аталған фигуралар түрінде емес, кез-келген қисықпен шектелген, еркін формадағы фигуралардың да ауданын табу қажеттігі жиі туады. Ал мұндай есептерді шешуде анықталған интеграл ұғымына, оның геометриялық мағынасына, сондай-ақ оның мәнін қалай есептеуге болатынына тоқталамыз.
Жұмыстың мақсаты: Анықталған интегралды жуықтап шешудің бірнеше әдістерін салыстыра отырып бағдарламалау, қателіктерді анықтау.
Сандық интегралдау - анықталған интегралдарды жуықтап есептеуге және дифференциалдық теңдеулерді жуық шешуге арналған математиканың бөлімі. Интегралдарды жуықтап есептеу формулалары квадратуралық формулалар деп аталады. Дифференциалдық теңдеулерді жуық шешудің көптеген аналитикалық әдістері бар. Олардың ішінде біртіндеп жуықтау әдістері, Чаплыгин әдісі, Риц әдісі, Галеркин әдісі т. б.
Сандық интегралдау инженерлік және ғылыми деректерді анализдеу немесе сараптау үшін қажетті. Интегралды классикалық әдістермен аналитикалық түрде алу мүмкін болмаған жағдайларда сандық интегралдау есебі қойылады. Кейде интеграл астындағы функция өте күрделі, кейде функцияның таблицалық мәндері ғана берілуі мүмкін.
Сандық интегралдауды сандық квадратура деп те атайды. Ал қолданылатын формулалар квадратуралық формулалар деп аталады.
Сандық интегралдау да дәл және жуықтау болып екіге бөлінеді.
Егер абсцисса өсі бойынан алынатын нүктелер бірқалыпты орналасатын болса, онда Ньютон - Котестің дәл квадратуралық формулалары қолданылады, басқа жағдайда жуықтау - Гаусс формулалары қолданылады.
Сандық интегралдаудың негізгі идеясы - интеграл астындағы функцияны [a, b] аралығында интерполяциялық полиномға жіктеу және полиномның әр мүшесін интегралдау арқылы есептеу процесін жеңілдету.
Интегралдың қателігін төмендету үшін интеграл астындағы функция анықталған [a, b] аралығы h қадаммен бірнеше аралыққа бөлу керек: x i+1 - x i =h, i=1, 2, …, n-1. Қадам тұрақты болған жағдайды қарастырайық.
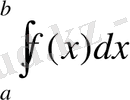 (1)
(1)
түрдегі интеграл берілсін.
 Анықталған интегралды есептеудің тік бұрыштар әдісі.
Анықталған интеграл
берілген
Анықталған интегралды есептеудің тік бұрыштар әдісі.
Анықталған интеграл
берілген
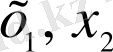 аралығындағы
аралығындағы
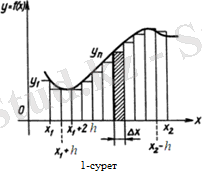
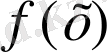 қисығы астындағы ауданға тең (1-сурет) .
қисығы астындағы ауданға тең (1-сурет) .
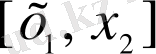 кесіндісін
кесіндісін
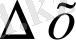 бөліктерге бөлеміз және ауданды тіктөртбұрышты жолақтар аудандарының қосындысы ретінде есептейміз:
бөліктерге бөлеміз және ауданды тіктөртбұрышты жолақтар аудандарының қосындысы ретінде есептейміз:
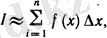 , мұндағы
, мұндағы
 жолақтар саны. Мұндай әдіс
«анықталған интегралды тік бұрыштар әдісімен алу»
деп аталады.
жолақтар саны. Мұндай әдіс
«анықталған интегралды тік бұрыштар әдісімен алу»
деп аталады.
[a, b] аралығынан х
0
бір түйін алатын болсақ, яғни
f
(
x
) =const болады, онда қарастырып отырған аралықта
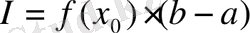 деуге болады.
х
0
нүктесін аралықтың тура ортаңғы нүктесі деп алсақ
деуге болады.
х
0
нүктесін аралықтың тура ортаңғы нүктесі деп алсақ
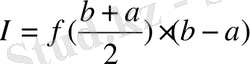 формуласы шығады, оны тіктөртбұрыштар формуласы дейді, әдістің қателігін азайту мақсатында аралықты бірнеше бөлікке бөліп, әр аралықты тіктөртбұрышпен толтырып, ауданын тауып, барлық аудандарды бір біріне қосады:
формуласы шығады, оны тіктөртбұрыштар формуласы дейді, әдістің қателігін азайту мақсатында аралықты бірнеше бөлікке бөліп, әр аралықты тіктөртбұрышпен толтырып, ауданын тауып, барлық аудандарды бір біріне қосады:
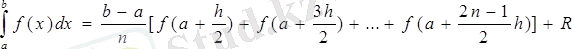 (2)
(2)

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz