Сжетті есептер

Жоспар
Кіріспе

1. Сюжетті есептердің мазмұны мен берілу компонеттері.
2 Математикалық модель құру
3 Математиканы оқыту әдістемесіндегі 5.6 сыныптардағы сюжетпен берілген есептерді шешу ерекшеліктері
4 Пәнаралық байланыс
5 Математикадағы сюжеттік ойындардың ерекшеліктері

Қазіргі дидактиканың барлық талабын қанағаттандыра отырып, эвристикалық әңгіме оқушыларға сабақ барсында танып білуміздің ең маңызды және тиімді әдістерінің қатарына жатады. Ол қазіргі жағдайда 5-9рии цифр ) сыныптарда математикадан жаңа материал өтуде және жаппай есеп шығартуда негізгі әдіс болуы керек. ол, әрине, мұнда басқа оқыту әдістерімен ұштастыра пайдалануы тиіс. Бұл тұрғыда алдыңғы қатарлы тиімді әдістер болып табылатын проблемалық-бағдарламалық жаңа әдістер алдыңғы кезекке шығады. Эвристикалық әңгіме синтетикалық әдістерден гөрі аналитикалық әдістермен жақсы үйлеседі.
Эвристикалық әңгіме-сұрақтар жүйесі бірсыпыра шарттарды қанағаттандыруы қажает: сұрақтар логикалық жағынан жүйелі, қысқа, дәл болуы; екі-ұшты,дүдәдәл болмауы, жауабы оп-оңай болмауы және оқушылардың көпшілігінің жан-жақты ойлауына жауабы дәл және толық, барлық сынып оқушыларына түсінікті болуы қажет.
Эвристикаға «дәндеп» алған шәкіртке «дап-дайын» жоспармен жұмыс істеу қызық болмай қалады,жалықтырады. Сабақ кезінде немесе үй тапсырмасын орындау кезінде болсын, мәсеоені шешу кілтін, есептерді шешудің жаңа жолдастарын оқушылардың өздері «ашуға» құмарлық пайда болады. Оларға эвристикалықәдіс-айлалар қолданатын жұмыстарға ынталы болады. Ал сайып келгенде, шәкірттердің математикалық талғамын жақсартып, математиканың незіздерін саналы түрде игеруіне игі әсер етеді.
Эвристикалық әдісті қолданудағы бір кемшілік- ол проблеманы үйретуде мұғалімнің өзі айту айту (ақпарттық) әдісіне қарағанда уақытты көп алады.

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 42 бет
Таңдаулыға:

0.1 Сюжетті есептердің мазмұны мен берілу компонеттері.
Сжетті есептердің түрлері.

Қазіргі таңда техникалық прогрестің дамуына сәйкес адамдар көптеген сұрақтарға жауап іздей бастады. Мысалы, қай банкке ақша салсам, белгіленген уақыт аралығанда қанша көлемді пайда түсіре аламын немесе Алматыдан шыққан пойыздың артынан 1,5 сағаттан соң шыққан жеңіл көлік, қанша уақыттан кейін қуып жетеді және де күнделікті өмірде біз жеңілдіктер кезінде дүкендер бағаның түсірілуін ұсынады, әрбір зат 50%-ға түсірлген деген айтуларды естиміз.Студенттер емтихан бағаларын жиі пайыз түрінде алады, мысалы, емтиханның өту үшін студент кем дегенде 40% жинау тиіс. Құрлыс қоғамдары қарыздарға өсірілімдер тағайындайды және өсірілімдер пайыздар ретінде беріледі, мысалы 4,75% . Осындай жағдайаттардан құралған есептерді де біз математика саласында қарастырып есептей аламыз.
Мысал1.1: Әр минут сайын арақашықтық неше метрге қысқарып отыр? Қанша уақыттан кейін оқушы әжейді қуып жетеді?

1.1-сурет

Үй
Мектеп
S=200 м
әже
Оқушы

Оқушы
110 м 1 минуттан кейін
? м

Ә.60 м

?
Ә.
3 минуттан кейін

? м
Ә.
4 минуттан кейін

? м

Ә.

Шешуі: 110-60=50ммин - оқушы мен әжейдің бір-біріне қуып жету жылдамдығы.
vжақын=v1-v21.1

Оқушы әжейді қуып жету үшін екеуінің арасындағы бастапқы 200 м арақашықтық жүріп өтуі керек.
20050=4мин

Есептерді шешу арқылы оқушылар жаңа математикалық білім жинақтап, оны күнделікті өмірде қолдануға даярланады. Есептер оқушылардың логикалық ойлау қабілетінің дамуына ықпал етеді. Есептерді шешу олардың тұлғалық қасиеттерін қалыптастыруға да көп әсерін тигізеді. Сондықтан мұғалімнің өзінің де есептер , олардың құрлымы туралы түсінігі болуы және есептерді түрлі тәсілдермен шеше білуі керек.
Есеп-табиғи тілде сипатталған, кейбір жағдаяттарға (жағдаятқа) немесе қандай да бір компонентіне сандық мінездеме беріп, компоненттерінің арасындағы кейбір қатынастардың барлығын немесе жоқтығын көрсету, әрі осы қатынастың түрін анықтау.
Кез-келген сюжеттік мәтінді есептер екі бөлімнен тұрады: шарты және талабы (сұрағы).
Есептің шартында объектілер және объектіні сипаттайтын шамалар, ол шамалардың белгілі және белгісіз мәндерді, олардың өзара қатынастары туралы мәлметтер беріледі. Есептің талабы (сұрағы)-ол нені табу керектігіне нұсқау. Ол бұйрықты сөйлем түрінде (тік төртбұрыштың ауданын тап), я сұраулы сөйлем түрінде (тік төртбұрыштың ауданы неге тең?)
Математикадан есептерді шешуде арифметикалық және алгебралық тәсілдерден басқа да тәсілдер қолданылады.
Мысал1.2. Екі елді мекеннен бір-бірімен қарама-қарсы екі жаяу шықты. Біреуі барлық жолдың 58 , ал екіншісі 310 бөлігін жүрді. Екі жаяудың кездесуі мүмкін бе? Екі елді мекеннің арасын кез-келген кесінді арқылы кескіндейміз (1.2-сурет).

310

58

1.2-сурет

Сосын фалес теоремасы бойынша кесіндіні 8 және 10 тең бөліктерге бөлеміз. Сызбаға сүйеніп есептің сұрағына тез жауап беруге болады:
"Кездеспейді". Есепті бұлайша шешу-графиктік тәсіл деп аталады. Ал, кейде есепті графиктік тәсілмен шешу кесінді салумен ғана байланысты болмайды, олардың ұзындығын өлшеумен де байланысты болады.
Мысал 1.3. Оқушылар мектеп жанына бірінші күні 3 терек және 5 қайың отырғызды. Ал, екінші күні сонша терек, ал қайың 2-ін кем отырғызды. Оқушылар екі күнде неше ағаш отырғызда? Әрбір ағашты ұзындығы 1см болатын кесіндімен кескіндеуге келісейік. Сонда екі күнде отырғызылған ағаштар 3-суреттегі ΑΒ кесінді түрінде болады. Барлық ағаштарды бейнелейтін кесіндіні өлшеу арқылы есептің сұрағына жауап аламыз: "Оқушылар екі күнде 14 ағаш отырғызды".
Кейбір есептерді заттарға амалдар қолдану арқылы шешуге болады.

3 т. 5 к. 3 т. В

2-і кем
1.3-сурет

Мысал 1.4. Шаруа қожалығының 40 ауылшаруашылық техникасы бар. Әрбір жүк машинасына 4 трактор сәйкес келеді. Қожалықта неше жүк машинасы, неше трактор бар? Әрбір техниканы таяқшалармен белгілейік (40 техника-40 таяқша) және әрбір жүк машинасына 4трактор сәйіес келеді. Бір таяқша-бұл жүк машина. Ал оның төменгі жағына 4 таяқша қоямыз-4 трактор. Ал оның төменгі жағына 4 таяқша қоямыз -4 трактор. Осылайша 40таяқшаны бөліп қоямыз. Есептің сұрағына жауап беру үшін жоғарғы бөлікте неше таяқша және төменде неше таяқша екенін санау жеткілікті болады.(1.4-сурет).

1.4-сурет
Есепті былайша шешуді практикалық тәсіл дейді. Бұл сюжетті есептерді шешудегі тағы бір тәсілі.
Сюжеттік есептің нақты анықтамасы жоқ, бірақ сюжетті есеп дегенімізөмірдегі шынайы болмыс пен объектілерді қолдана отырып мәтін мен берілген есептерде шешуде қолдану.

Көп жағдайлардағы сюжеттік есептердің бірілу түрлері:
Қоспалар, қорытпалар қатысты есептер;
Экономикалық мазмұндағы есептер;
Қозғалысқа қатысты есептер;
Геометриялық мазмұндағы есептер,
Концентрация мен пайыздық құрамға есептер т.с.с

Мысал:
1. Мыс пен қалайы балқымаларының екі кесегі бар. Біріншісінде 40% , екіншісінде-32% мыс бар. Мысы 35% болатындай жаңа 8 кг балқыма алу үшін осы кесектердің салмағы қандай болу керек?

1-кезең. Математикалық модельге негізделініп құрылған болжамдарды ерешелеп (бөліп ) алу;

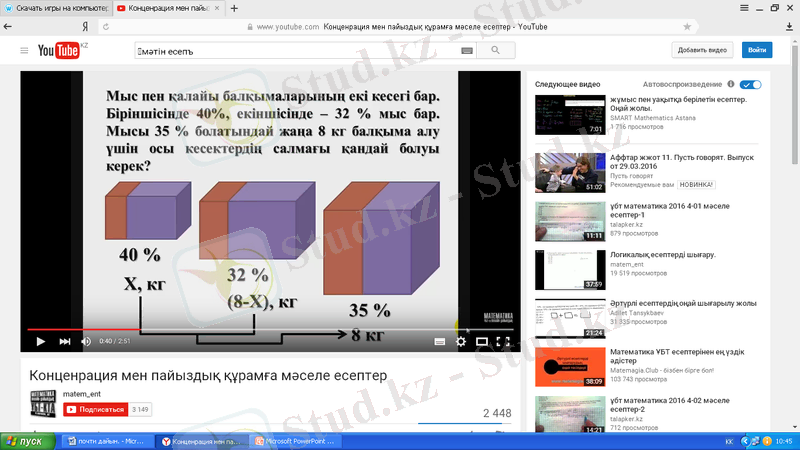
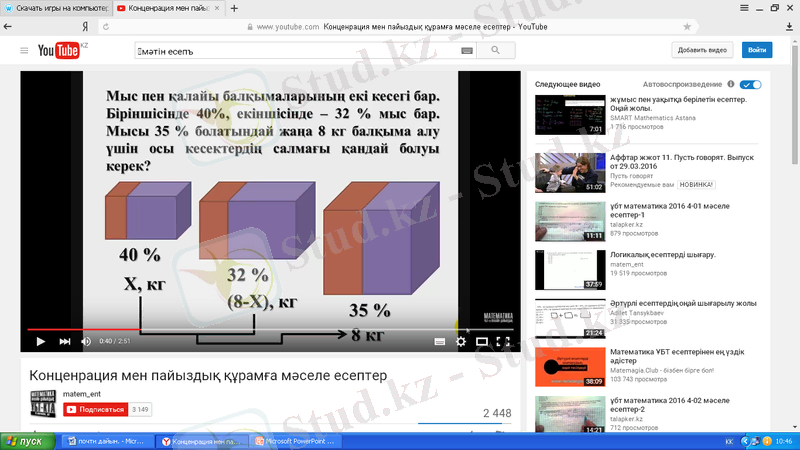
40%32 %35 %

x , кг8-x, кг8 кг

2-кезең. Бастапқы берілгендер және нәтижелер нелер болатындығын нақты анықтау;

Бұл кесте таза салмағы, концентратциясы және массасына байланысты құрылған;
Концентратцияа байланысты мынадай формула бар
mA=M*CA
mA- таза салмағы
M- барлық салмақ
CA- концентратция

3-кезең. Нәтижелерді бастапқы берілгендермен байланыстаратын математикалық қатнастарын жазу;
1.Осы есептің математикалық модельін құру үшін кестені пайдаланамыз:

mA=M*CA
mA
M
CA

2.Енді кестені толтырамыз:

mA=M*CA
mA
M
CA

0,4x

x

0,4

0,328-x

8-x

0,32

0,4x+0,328-x

8

0,35

3.Осы кестедегі ақпарттарды пайдаланып теңдеу құрамыз:

0,4x+0,328-x=8*0,3

Көптеген сюжетті есептерді шығару кезінде квадрат теңдеулер қолданылады. Сызықты теңдеу арқылы шығарылатын сюжетті есептердің едәуір бөлігі арифметикалық, кейбір жағдайларда жасанды түрде шығарылуы мүмкін. Ал квадрат теңдеулерге келтіретін сюжетті есептер арифметикалық жолмен шығарылмайды.
Мәтінді есептің берілгені бойынша квадрат теңдеуді құрудың негізгі кезеңдері сызықтық теңдеу шығарылатын есептермен бірдей.
Мысал2. Пәтерде ендері бірдей екі бөлме жасау жобалануда (12-сурет). Бірінші бөлменің тұзындығын енінен 1,5 есе артық, ал екінші бөлменің ұзындығын 7,2 м. Егер пәтердің ауданы 56,7 м2 болса, оның онда бөлмелердің енін табыңдар.
1-кезең. Математикалық модельге негізделініп құрылған болжамдарды ерешелеп (бөліп ) алу;
1,5 х

х

х

7,2
2-кезең. Бастапқы берілгендер және нәтижелер нелер болатындығын нақты анықтау;

Бөлменің енін -x м арқылы белгілейік. Сонда бірінші бөлменің ұзындығы 1,5 x, ал ауданы 1,5x∙x м2 болады. Екінші бөлменің ауданы 7,2∙x м2 береді.
Енін -x белгілейміз;
3-кезең. Нәтижелерді бастапқы берілгендермен байланыстаратын математикалық қатнастарын жазу;
Есептің шарты бойынша
1,5x2+7,2x=56,7
немесе
3x2+14,4x-113,4=0
Соңғы квадрат теңдеуді шешіпx1=4,2 және x2=-9 түбірлерін аламыз. Бұл сандар есептің шарты бойынша құрылған квадрат теңдеуді қанағаттандырады. Бірақ есептің шешімі тек 4,2 сан болады, себебі бөлменің ені оң сан болу керек. Тексеру жүргізу арқылы 4,2 м есепті қанағаттандыратынды аламыз.

Сюжетті есептердің мазмұнын талдау жолдары.

Есепті арифметикалық тәсілмен шешу кезеңдері.
Есепті арифметикалық тәсілмен шешу-өте күрделі жұмыс, ол нақты мазмұнына және шығарушының білігіне де байланысты. Есепті шешудің мынадай бірнеше кезеңін бөліп көрсетуге болады:
1. Есептің мазмұнын түсіну,қабылдау және талдау.
2. Есепті шешу жоспарын іздестіру және құру.
3. Есепті шешу жоспарын орындау, жүзеге асыру. Есептің талабының орындалуы туралы қорытындыны тұжырымдау (есептің сұрағына жауап).
4. Есептің шешуін тексеру және жіберілген қателерді түзету.
Есептің талабының орындалуы туралы толық қорытынды тұжырымдама жасау немесе есептің сұрағына жауап беру, яғни есепті шығару барсындағы кезеңдер бір-бірінен нақты ажыратылып көрсетілмейді және қашанда бірдей толық орындалмайды. Кейде есепті оқып танысу барсында есепті шешушіге мұндай түрдегі есептер оған бұрынан таныс болып, есепті шығару жолын білуі мүмкін. Мұндай жағдай есептің шешімін іздезтіру жолы жеке кезеңдерге жіктелмейді және алғашқы үш кезеңдерге жіктелмейді және алғашқы үш кезеңнің әрбір адымын талдап түсіндіріп, есепті орындап болғанда оны тексеру қажет болмайды. Бірақта есепті орындап оны қажет болмайды. Бірақта есепті шешудің толық логикалық желісін орындау осы аталған кезеңдердің бәрін қамтиды. Ал есепті шешудің әр кезеңінің мүмкін тәсілдерін білу кез келген есепті шешу үрдістердің түсінікті болуын және бағытталғандығын, яғни оның дұрыс шешілуін қамтамасыз етеді. Есепті шешудің бірінші кезеңнің негізгі мақсаты есепте берілген тұтас жағдайды орындаушының түсінуі, есептің шартын, оның талабын, яғни сұрағын, есептің мәтінінде кездесетін барлық терминдер мен таңбалардың мағынасын жете түсіне білу. Есептің мазмұнын түсінуге көмектесетін бірнеше тәсілдер белгілі.
Мысал1.5. Жолмен бір бағытта екі бала келе жатыр.Алғашқыда екеуінің арасы 2 км болды. Бірақ алда келе жатқан баланың жылдамдығы 4 кмсағ, ал одан кейін келе жатқан баланың жылдамдығы 5 кмсағ,сондықтан екінші бала біріншіні қуып жетеді. Қозғалыс басталғаннан екінші бала біріншіні қуып жеткенге дейін екеуінің арасында 8кмсағ, орташа жылдамдықпен ит жүгіріп жүр. Ол артта келе жатқан баладан алдағыға дейін жүгіріп барып, қайтадан кейін қайтады. Осылайша балалар қатарласқанша ерсілі-қарсылы жүгірі береді. Ит уақыт арасында қандай қашықты жүгіріп өтеді?
Есептің мазмүнын түсініп үшін, оның шарты мен талабын жіктеп, мәтін бойынша арнайы сұрақтар қойып,оларға жауап беру керек.
Есеп не туралы? (Есеп екі бала мен иттің қозғалысы туралы. Қозғалыс оған қатысушылардың әрқайсысының жылдамдығы, уақыты және жүрілген жолы арқылы сипатталады).
Есепте нені табу керек? (Есепте иттің осы уақыт аралығында жүрген жолын табу керек).
"Осы уақыт аралығанда" деген сөз тіркесі нені білдіреді? (Есепте ит екі баланың арасында "қозғалыс басталғаннан екінші бала біріншіні қуып жеткенге" дейін жүгіреді делінген. Сондықтан "осы уақыт аралығында" деген "қозғалыс басталғаннан екінші бала біріншіні қуып жеткенге дейінгі уақыт аралығы" дегенді білдіреді).
Есепте қозғалысқа қатысушылардың әрқайсысы туралы не белгілі? Есепте мыналар белгілі:
+ Балалар бір бағытта келе жатыр;
+ Қозғалыс басталғанға дейін екеуінің арасы 2 км;
+ Алда келе жатқан екінші баланың жылдамдығы 4 кмсағ;
+ Одан кейін келе жатқан екінші баланың жылдамдығы 5 кмсағ;
+ Иттің жүгіру жылдамдығы 8 кмсағ;
+ Қозғалысқа қатысушылардың, яғни екі баланың арасы 2 км болғандағы қозғалыс бастал,аннан екеуінің кездесуіне денйінгі қозғалыс уақыты бірдей.
Есепте не белгісіз ? (Есепте екінші бала бірінші баланы қанша уақыт аралығында қуып жететіні белгісіз, яғни қозғалысқа қатысушыларға ортақ уақыт белгісіз. Балалардың жақындасу жылдамдығы да белгісіз-мұны есепте анықтау талап етіледі).
Не ізделінді: сан ба, шаманың мәні ме, кейбір қатынастың түрі ме? (Шаманың мәні ізделінді тұр. Қозғалысқа қатысушыларға, бәріне ортақ қозғалыс уақыты аралығында иттің жүгіріп өткен қашықтағы ізделінді).
Есептің мазмұнын түсінуге және есепті шешу жолдарын іздеуге негіз жасау үшін-есептің мәтінін сипатталған жағдаят барлық қатынастарды, байланысты және сандық деректерді сақтай отырып, басқаша тұжырымдалады. Әсіресе, бұл тәсілді есептің мәтін мағынасы бойынша бөліктерге бөлумен байланыстыра жүргізу нәтижелі болады. Қайта тұжырымдау бағыты мынадай болуы мүмкін: артық, негізгі емес мәлметтерді алып тастау; сәйкес терминдермен кейбір ұғымдардың сипатталуын ауыстыру және керісінше, кейбір терминдерді сәйкес терминдерді сәйкес ұғымдардың мағынасын сипаттау арқылы беру; есептің мәтінін шешу жолын іздестіруге қолайлы түрге түрлендіру, қайта тұжырымдаудың нәтижесі негізгі жағдайларды ажырату, сонымен жоғарыда келтірген қозғалысқа берілген есепті былайша қайта тұжырымдауға болады.
"Бірінші баланың жылдамдығы 4 кмсағ. Ал екінші оны қуып жетуші баланың жылдамдығы 5 кмсағ (есептің бірінші бөлімі).Балалардың арақашықтығы 2 км (екінші бөлім). Балалардың жолдағы уақыты-бұл екінші баланың бірінші баланы қуып жетуге кететін, яғни екінші баланың біріншіден 2 км артық жүретін жолға жұмсайтын уақыты (үшінші бөлім). Иттің жүгіру жылдамдығы 8 кмсағ. Иттің жүгіру уақыты балалардың кездесуге дейінгі уақытына тең. Иттің жүгірген қашықтығын анықтау талап етіледі". Әдетте қайта тұжырымдалған мәтінді схемалы түрде жазу тиімді болады. Есептің мазмұнын қайта тұжырымдаған соң мынадай кесте түрінде жазуға болады:

Жылдамдық
Уақыт
Қашықтық
Ит 8 кмсағ

1 бала 4 кмсағ

2 бала 5 кмсағ
?

? бірдей

?
?

? 2 км артық

?

1.6-сурет

Мысал1.6.Кейде қайта тұжырымдалған мәтіннің схемалы жазылуы басқа түрде беріледі. Есеп: "Турист жылдамдығы 56 кмсағ пойызбен 6 сағат жол жүрді. Бұдан соң оған әлі де жүрілген жолдан 4 есе артық жол жүру керек. Ол барлығы неше километр жол жүруі керек?" Есепті қайта тұжырымдасақ мына түрде болады: "Турист 56 кмсағ жылдамдықпен 6 сағ жол жүрді. Одан 4 есе артық жол жүруі керек. Барлық жолды табу керек". Бұл есепті схемалық түрде былайша жазуға болады:

Жүрді _______________ 56 кмсағ-тан ____________ 6 cағат
?
Қалда _______________ ?, 4 есе артық

1.7- сурет

Келтірілген жазуларда есепте сипатталған барлық жағдайлар, берілгені, ізделінді шамалар және олардың арасындағы қатынастар көрсетілген.
Есепті талдаудың маңызды құралы-сызба. Мысалы, соңғы есепке байланысты мынадай сызба орындауға болады (1.8-сурет)

4 есе артық
56 кмсағ

?

?
1.8-сурет

Шамалардың арасындағы тәуелділік пен барлық байланыстарды сызбада көрнекі түрде көрсету есептің шешуін іздестіруді жеңілдетеді.
Есепті арифметикалық тәсілмен шешу жоспарын әздестіру жолдарының кең тараған түрлерінің бірі-мәтіні бойынша есепті (берілгені немесе қайта тұжырымдау) талдау. Мәтін бойынша есепті талдау есептің берілгендерінен, я сұрағынан бастап тізбектей ой жүгірту арқылы жүргізіледі. Есепті берілгеннен сұрағанына қарай талдағанда мәтіннен екі берілгені бөліп алынып, олардың арасындағы байланыстардың көмегімен не белгісіз және оны қандай арифметикалық амал арқылы табу керектігі анықталады. Сосын бұл белгісізді берілген деп есептеп, қайтадан тағы екі өзара байланысқан берілгендері (шамаларды) бөліп алып, осылар арқылы табуға болатын белгісізді анықтайды және орындалатын арифметикалық амалды көрсетеді. Осылайша ізделенді шаманы табуға көмектесетін амал анықталғанша талдау жалғаса береді.
Есептің шешімін іздестіру сызба және схемалық жазу арқылы да жүргізіледі. Сызба арқылы шешімді іздестіру:
Мысал1.7.Бидонда сүт бар. Әуелі оның жартысын және 5 л, ал сосын қалған сүтті құйып алды. Сонда бидонда 10 л сүт қалды. Алғашқыда бидонда неше литр сүт болды?" АВ-кесіндісі ізделінді шаманы бейнелесін (6-сурет).
Сызбада кесінді тең екі бөлікке бөлінген: AO-OB.AO кесіндісі бірнеше кесіндісі бірнеше кесіндідентұрады. 10 л бейнелейтін кесіндіні үштен екі тең бөліктерден құралады. Срнда бұлардың бір бөлігі 102 л, яғни 5 л болды. Онда есептің сұрағына жауап беру үшін 5-ті 4-ке және 2-ге көбейту жеткілікті. Белгіленген жоспарды орындасақ

102=5л, 5*4*2=40л.

А О В

10 л 5 л

1.9-сурет

Мына есепті шешу жоспары есептің мәтінін кестенің көмегімен жазғанда жеңіл табылады.
Мысал1.10. 12 кг металдан 8 сайман даярланса, 36 кг металдан қанша сайман даярлауға болады?

Бір сайманның массасы
Саймандар саны
Барлық саймандардың массасы
Бірдей
8
12 кг

?
36 кг

Кесте бағандарына үш шаманың мәндері жазылған. Бірінші жолға жазылған белгілі екі шаманың мәндері арқылы үшінші шаманың мәнін, яғни 1 сайманның массасын табуға болады. Сонда екінші жолда екі шаманың мәндері белгілі болады, олар арқылы ізделінді саймандардың санын табуға болады.

Математикалық модель құру

Оқушылар сюжетті есептерді көбірек шығару олардың ойлау қабілетінің дамуына көптеп көмегін тигізеді. Математикалық модельін құрмас бұрын, модель дегеніміз не?, және математикалық модельдің тізбектеріне тоқталайық.
Модель - жасанды құрылған объект. Өйткені оқушылар оригинал объектіні схема, сызба, математикалық таңбалар, өрнектер және қатынастар, физикалық формулалар және т.б. түрінде бейнеленеді (көрсетеді). Қазіргі кезде кеңінен ең көп таралған қарапайым модельдерге: графикалық модель (объектіні сурет, кескін, схема, т.б. түрінде бейнеленген); математикалық модель (объектінің заңдылықтарын, әсерін, қасиетін математикалық өрнектер, қатынастар, заңдылықтар бойынша бейнелеу) т.б. жатады.
Есептің модель құру дегеніміз қойылған есепті ыңғайлы болатындай түрге келтіру.
Математикалық модель-бұл қарастырып отырған объектінің, процесстің, құбылыстың басты маңызды қасиеттерін көрсететін математикалық өрнектер.
Математикалық модельін құру мына тізбектерден тұрады:
1. Математикалық модель негізделініп құрылған болжамдарды ерешелеп (бөліп ) алу;
2. Бастапқы берілгендер және нәтижелер нелер болатындығын нақты анықтау;
3. Нәтижелерді бастапқы берілгендермен байланыстаратын математикалық қатнастарын жазу;

Мысал1. Автомобиль A елді мекеннен шығып, 50 кмсағ жылдамдықпен жүрсе, Bелді мекеніне межелеген уақытта жетеді. Егер автомобиль жылдамдығын 10 кмсағ арттырса, B елді мекеніне межелеген уақыттан 1 сағат бұрын жетеді. Aжәне B елді мекендерінің арақашықтығы неше километр?

1-кезең. Математикалық модельге негізделініп құрылған болжамдарды ерешелеп (бөліп ) алу;
Бізде 2 жағдай қарастырылған;
1) 1-жағдай бойынша жылдамдығымыз 50 кмсағ;
2-жағдай бойынша жылдамдығымыз 10 кмсағ арттырғандықтан
60 кмсағ болады;
2) 1-жағдай бойынша уақыт берілмеген, сондықтан оны t белгілейміз;
2-жағдай бойынша 1 сағат бұрын жетеді деген, яғни 1-жағдайдағы
уақыттан 1 сағат аз кетеді t-1;.
Бізге екі жағдайда бір аралықта жүргені белгілі S;

2-кезең. Бастапқы берілгендер және нәтижелер нелер болатындығын нақты анықтау;
v1(жылдамдық)=50 кмсағ ;
v2жылдамдық=60 кмсағ ;
t1(уақыт)=t белгілейміз;
t2уақыт=t-1 белгілейміз;
S жол=S1белгілейміз;
S жол=S2белгілейміз;

3-кезең. Нәтижелерді бастапқы берілгендермен байланыстаратын математикалық қатнастарын жазу;
1.Осы есептің математикалық модельін құру үшін кестені пайдаланамыз:

S
v
t
1

2

2.Енді кестені толтырамыз:

S
v
t
1

2

3.Осы кестедегі ақпарттарды пайдаланып теңдеу құрамыз:
-Берілген есеп жылдамдыққа қатысты болғандықтан, осы S=vt формуланы пайдаланамыз;
-Енді теңдеуді жазайық:
S=50*t
S=60*t-1
Осы берілгендер арқылы жүйе алдық. Оң жақтары S тең болғандықтан, оның сол жақ теңдіктері де тең
50*t=60*t-1
50*t=60t-60
60=60t-50t
60=10t
t=6
Енді t-ны бастапқы теңдеуге қоямыз.
S=50*6=300
Жауабы: S=300 км.

1.1 Пропедевтика алгебраического метода решения текстовых задач

Кез-келген өркениетті елдің экономикалық - индустриялдық дамуына әсер ететін ол-білім. Білімнің жаңа құрлымын қалыптастыру бүгінгі күннің көкейкесті мәселесі болып отыр. Осы тұрғыдан алғанда мектеп оқушысының есепті шығара білуі міндетті түрде меңгеруге тиіс білім болып саналады. Білім берудің басты факторы бұл-пән мазмұнның оқыту үйлесімділігі. Осындай оқыту үрдісінде алгебралық әдісті сюжеттік есептерде шығаруда білім берудің белгісі ретінде ұстануы, оны білім мазмұнында қолдану математиканы оқыту әдістемесінің жаңа талаптарымен толық сай келеді.
[2.2]Көптеген ғалымдар есептің анықтамалары мен белгілеріне көптеп түсініктер берді. Мысалға, К.Лейбництің айтқан сөзіне тоқталсақ, Есептерді әртүрлі амалдар мен әдіс-тәсілдер арқылы шығару есептің нақты, дәл, дұрыс және дәлелдеулерін тереңдету барысында әрбір есептің шешімдерін тауып, мақсатымызға жетуге болады-делінген. Сондықтан есептерді шешуде алгебралық әдісті қолдану заман талабы.
[2.3] Мәтінді, сюжетті, кестелік есептерді шығарғанда оқушылардың назарын есепті шығарудың тиімді арифметикалық және алгебралық әдістеріне назарын аудара отырып, алгебралық тәсілдің артықшылығын жүйелі түрде ашып беріп отыру қажет.
[2.1] Оқушылардың есептеу қабілетінің жоғарғы деңгейіне көтеруіне, сюжеттік есептерді шығарудағы терең логикалық ойлау мен функционалдық идиялардың тууына әсер етеді. Оқушы мәтіндік және сюжеттік есептерді шығару барсында ойлау қабілетін жүйелей отырып және өмірдегі шынайы болмыс пен объектілерді қолданады.
[2.1] 4-8 сыныптар арасында математикалық курсында мәтінді есептерді шығару жолын 2 түрлі тәсілмен көрсетілген:
1. Арифметикалық
2. Алгебралық
-Арифметикалық тәсіл- барлық логикалық операциялар нақты сандар арасында арифметикалық амалдар қолдана алу білімін пайдаланып негізгі тұжырымға негізделеді.
-Алгебралық тәсіл- есептерді теңдеу құру арқылы шығарылады.
[2.1] Кейбір мәтінді есептерді теңдеу шешу барсында пропедевтикалық жұмысына тоқталайық.
[2.1]Пропедевтикалық жұмыс көбіне 4-5 сыныптар да, ал қарапайым мәтіндік сюжеттік есепрді шешу 1-3 сыныптарда кездеседі. Осы негізде екі негізгі этап бойынша қарастырумызға болады.І этап бойынша, мұғалім оқушыларға мәтіннің жалпы математикалық түсініктерін береді. Ал ІІ этапта, мәтіндік сюжеттік есептерді математикалық тілге аудару және оның ненпорпормрлмрмлриоидтждэ
Мысалы 2.1. [2.4] Үй мен дүкеннің арасы 320 м. Айдос минут сайын 60 м жүреді. Ол 3 мин жүрді. Дүкенге жету үшін ол тағы неше метр жүруі керек?
І этап бойынша, мұғалім мәтін бойынша әңгіме жүргізеді және мұғалімнің көмегімен есептің моделін құрады.
ІІ этап бойынша, есептің жұмыс істеудің келесі кезеңі, есептің алгоритмін құру, ол үшін есептің моделі бойынша талдайды. Мұғалім оқушыларға мақсатты талдау бойынша сұрақтар қояды (сұрақтан берілгенге қарай)?. Мұғалім оқушыларға сұрақ қоя отырып, есепті талдайды.

+ Есепте нені білу керек? (Оқушылар Айдостың дүкенге дейін қанша жол қалғанын).
+ Қанша қалғанын білу үшін не істейміз?(Арақашықтық қанша және Айдос қанша жол жүріп өтті?)
+ Қалған жолды қандай амал арқылы табамыз? (Азайту)
+ Үйден дүкенге дейінгі ара қашықтықты білеміз бе? (Ия, 320 м)
+ Айжан қанша жол жүріп өткенін білеміз бе? (Жоқ. Бірақ ол әр минут сайын 60 м жүргенін білеміз.)
+ Айдос жолда қанша уақыт болды? (3 минут)
+ Жүріп өткен жолын қандай амалмен табамыз? (Көбейту)
Осындай жұмыстың нәтижесінде теңдеу құру арқылы шығарамыз. Белгісіз шаманы анықтап, оны x деп белгілейміз, белгілі мен белгісіз айнымалылар тең қатынасымен өрнекті анықтап, теңдеу құрамыз. Келесі кезең,теңдеуді шешеміз, бұл жерде белгісіз x-ті табамыз. Сонымен, мәтінді есеппен жұмыс істеу нәтижесіндегі жазылу моделі:
Болғаны-320 м
Жүргені-? м минут сайын 60м, 3мин.
Қалғаны-? x м
Есепті теңдеу құру арқылы шығарайық:
x+60x3=320
x+180=320
x=300-180
x=140
140+180=320
320=320
Бұл екі этап бойынша қарастырылған қарапайым мысал болатын, енді осы екі этапқа толық тоқталып өтейік.
Проветикалық І этап. Осы І зерттеу этабында оқушылар мәтіндік есептерді шешу үшін ең маңызды жүйелерді қалыптастыру қажет, оларға мыналар жатады: мәтінді түсініп оқу дағдысы; берілген мәтіндік есептің шарты мен сұрағына талдау жүргізу дағдысы; қысқартылған мәтін ензігу дағдысы; мәтіндік есепті сызбалар (сюжет) арқылы орындау дағдысы.
Приемы, формирующие умение читать текст задачи:
+ Дұрыс оқу мәселелеріндегі үлгілерін көрсету;
+ Мәтіндік есептердің негізгі мәселесі оның мазмұнын игеру. Бұл жерде әртүрлі формадағы есептер ұсынылған: мәтін, қысқартылған мәтін, сюжетпен. Сондай-ақ, есептің мазмұнын меңгеру бойынша әдістер енгізілген: есептің сандық деректерін өзгерту; сюжеттік есепті өзгерту; сандық деректер мен сюжетті өзгерту.
Приемы, формирующие умения вы

Математиканы оқыту әдістемесіндегі 5-6 сыныптардағы сюжетпен берілген есептерді шешу ерекшеліктері

Математиканы оқыту әдістемесіндегі 8-9 сыныптардағы сюжетпен берілген есептерді шешу ерекшеліктері.
Математиканы оқыту әдістемесіндегі 8 бен 9 сыныптардағы сюжетпен берілген есептерді шешу ерекшеліктеріне тоқталып өтейік. Негізі мектеп оқулықтарында арнайы сюжет пен берілген есептерге әдістемелік нұсқаулық жоқ десек те болады, сюжетпен берілген есептерді көбіне мәтіндік есептерден бөліп алып қарастырып келміз.
Енді Шыныбековтың Жалпы білім беретін мектептің 8- сыныбына арналған оқулықтағы,Алгебрасындағы ІІ тарау Квадрат теңдеулер, тарауындағы Квадрат теңдеулергеге келтіретін есептерді қарастырайық.
Есептерді теңдеу құрып шешу негізінен үш кезеңнен тұратыны бұрын айтылған, оны тағы да қайталайық.
1. Есептің шартындағы белгілі және белгісіз шамалар арасындағы қатынасты, тәуелділікті теңдік түрінде жазамыз, яғни теңдеу (есептің математикалық моделін құрамыз)
2. Теңдеуді белгілі алгоритмді қолданып шешеміз, оның түбірлерін табамыз.
3. Теңдеу түбірлерінің есеп шартын қанағаттандыратыныанықтап алынады.
Егер бұрынғы өтілген тақырыптар да бір шешімі болатын немесе бірде-бір шешімі жоқ жоқ болатынекі жағдай кездесетін болса, онда берілген пунктің есептерін шешкенде мынадай үш жағдайдың болуы мүмкін. Есептің екі шешімі, бір шешімі болуы және бірде-бір шешімі болмауы мүмкін. Есептің екі шешімі болатын жаңа жағдай оқушылар үшін белгілі бір қиындықтыр туғызды және оны түсіндіруді қажет етеді. Мұндай есеп көбіне бірқалыпты үдемелі (кемімелі) қозғалыстарға берілген есептерде ұшырасады. Табылған түбірлер есептің барлық шарттарына сәйкес екендігін айқындау-есептерді шешудің қажетті құрамдас бөлігі. Табылған шешімдерді осылайша зерттеуді есептің шешуін тексерумен шатастырмау керек.
Шешуін тексеру дидактикалық тапсырма болып табылады және оның зерттей білу дағдысын қалыптастыру үшін пайдасы бар. Жаттығу мақсатында түрлі шамаларды белгісіз деп қабылдап, есепті бірнеше тәсілмен шешуге болады.
Есеп шешуін тексерудің қажеттілігі жөнінде біржақты ұсыныс жасауға болмайтыны анық. Бұл мәселені нақтылы жағдайға байланысты және бірнеше кезекте уақыт қорының жеткілікті болуына қарай мұғалімнің өзі шешеді.
Есептерді шешуге бөлінетін артық уақыттың болмауын ескере отырып, кейбір жағдайларда әрдайым есептің шешуін жауабына дейін жеткізбей, теңдеулер құрумен шектелген жөн. Өйткені, сабақта 3-4 есеп құрастыру мүмкін болады (мұның ішінде бір ғана есепті шешу үшін бірнеше тәсілмен теңдеу құру да бар.)
Теңдеулер құрып, есептер шешудің маңызы-математиканың пайдасын, оны қолданудың универсалдығын, математикалық абстракты түсініктерді түрліше талқылауға болатындығын көрсетуге мүмкіндік береді. Негізгі мектептің төменгі сыныптарында, математикалық түсініктердің жалпылығын көрсету үшін математикалық моделі (теңдеу, формула) бірдей болатыны мазмұны әр түрліесептерді түзуге біраз мысалдар қарастырылады. Жоғарғы сыныптарда математиканың өмірмен байланысын, басқа пән материалдарын пайдалану арқылы көбірек көрсетуге болады.
Енді осы теңдеу құру арқылы есептер шешуге тоқталайық. Теңдеу құру арқылы есептер шешудің ең қиыны есептің математикалық моделін (теңдеу немесе теңдеулер жүйесін) құру, әсіресе, қиындық тудыратын есептің шешуін жазбаша жазу болып табылады. Сондықтан оқушылардың назарын есептің шешуін жазу тәсілдеріне аударған жөн.
Оқулықтың негізгі мәтінінде келтірілген есептерді типі бойынша шартты түрде теңдеудің сөзбен тұжырымдамасы болатын есептерге, геометриядан алған білімдерді пайдалануды қажет ететін, және ең соңында, шамалары тура және кері пропорционал тәуелділікте болатын есептерге (бұрын бірқалыпты қозғалысқа және бірлесіп істелген жұмысқа арналған есептер жатады) бөлуге болады.
Бір ғана y=kx функциясы (тура пропорционал тәуелділік) табиғаты алуан түрлі болған шамалар арасындағы тәуелділікті өрнектеуге мүмкіндік береді.
Мысалы: m=pV-заттың тығыздығы тұрақты болғанда, оның масасы m мен көлемі Vарасындағы;
S=vt -бірқалыпты түзу\сызықты қозғалыс кезіндегі жол S мен уақыт tарасындағы;
C=PIdPI=3.14 ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.