«Математикалық модельдер және сандық әдістер байланысы туралы»

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 70 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым Министрлігі

Тараз Мемлекеттік педагогикалық институты

Садуақасова Құлпынай Мұхамеджанқызы

Тақырыбы:

«Математикалық модельдер және сандық әдістер

байланысы туралы»

ДИПЛОМДЫҚ ЖОБА

Мамандығы:

«»

Тараз - 2012 жыл

Мазмұны

Кіріспе

Бірінші тарау

Модельдеу және сандық әдістер

Модельдеу және сандық әдістер туралы
Компьютер көмегімен математикалық

есептерді шығару технологиясы туралы

Модельдер және модельдеу негіздері.

Математикалық және компьютерлік модельдеу

Модельдеу және сандық әдістер, компьютер

көмегімен есеп шығаруда тиімді әдістерді

(тәсілдерді) таңдау ерекшелігі

Екінші тарау

Модельдеу және сандық әдістер ерекшеліктерін оқушылардың математикалық білімдерін тереңдетуде пайдалану

2. 1. Компьютер көмегімен есеп шығару технологиясын

оқушылардың білімін және біліктілігін тереңдету,

дамытуда пайдалану ерекшеліктері

2. 2. Оқушылардың танымдық және математикалық

білім деңгейін тереңдетудегі модельдеудің

маңызы (рөлі)

2. 3. Сандық әдістердің математикалық білімді

және біліктілікті тереңдетудегі орны

Қорытынды

Пайдаланылған әдебиеттер тізімі

Кіріспе

Математика - ғылымдардың патшасы деп бекер айтылмаған. Қазіргі заманғы жаңа жоғарғы технологиялардың, оның ішінде ақпараттық технологиялардың және білімнің, барлық ғылым бағыттарының, экономиканың тиімді дамуы математикасыз тіпті мүмкін емес.

Ел Президенті соңғы жылдардағы Қазақстан халқына арнаған Жолдауларында үнемі жаратылыстану ғылымдарының, оның ішінде, әсіресе, математика ғылымының дамуына, жастарға математикалық білім беру мәселелеріне баса назар аударып келеді. Сондықтан, Қазақстан Республикасы білім және ғылым министрлігінің бірінші болып республика математика мұғалімдері съезін өткізу туралы шешімі өте құптарлық, өз уақытында өткізілген іс-шара болды деп есептейміз. Өйткені, математикалық білімді мазмұнды жаңарту және оны жаңа сапалық деңгейге көтеру, қазіргі қоғам дамуы талабына сай ету, бүгінгі күннің заңдыда және өзекті мәселесі болып отырғанын қоғамның даму қарқыны көрсетіп отыр.

Математика пәнін оқыту жағдайын жуық арада жаңа сапалық деңгейге көтере және шығара алсақ, онда қоғамдағы, білімдегі, ғылымдағы, мәдениеттегі, тәрбиедегі және экономикадағы көп мәселелер өз оң шешімін өзінен өзі табатындығы сөзсіз. Мысалы, жаңа қоғамның және республиканың индустриялдық-инновациялық дамуы кезеңіндегі математика ғылымының дамуы және оны оқыту сапасының жақсаруы, біліктілігі жоғары сапалы, халықаралық талаптар деңгейіндегі инженерлер және технолог мамандар, кәсіби деңгейі жоғары, сауатты экономистер, қаржыгерлер, заңгерлер және менеджерлер дайындауға мүмкіндік берер еді.

Мaтематикa курсының мaмaндыққa бayлyды және оның қолданбалылығын дәлелді ететін тарауларының бipi - мoдeльдey. Қaзipгi мемлекеттік тілдегі инфopмaтикaны oқытy әдicтeмeci оулықтарында және қосымша оқу құралдарында aқпapaттық тexнoлoгиялap, aлгopитмдey жәнe пpoгpaммaлay мәceлeлepiн оқып-үйрену салыстырмалы тepeңірек және жaн-жaқты зepттeлyдe, оқытылуда. Ал мoдeль ұғымын және мoдeльдey пpoцeciн мектеп деңгейінде оқып-үйрену мәселелеріне бүгінгі қолданыстағы математика және информатика оқулықтарында жеткілікті нaзap ayдapылмaған. Шын мәнiндe, oқyшылapдың бoйындa жүйeлiк-aқпapaттық танымдық тәciлдepдi қалыптacтыpyғa нeгiздeлгeн мoдeльдey пpoцeci (математикалық модель) - ғылыми тaным әдici peтiндe қapacтыpылып, фopмaлизациялау пpинципi мeн кoмпьютepлiк мoдeльдey құpылымын мeңгepyдiң ceнiмдi құpaлы бoлып тaбылaды.

Біздің дипломдық жұмыстағы қойып отырған мақсатымыз - модельдеу және есепті шешу әдістері арасындағы байланысты оқушылар білімін тереңдетуде, дамытуда пайдалануды көрсету. Өйткені, бүгінгі күні кез келген ғылыми және практикалық (өмірлік) есептерді компьютер көмегімен шешу математикасыз, модельдеусіз және сандық әдістерсіз мүмкін емес.

Дипломдық жұмыс кіріспеден, екі тараудан, қорытындыдан және әдебиеттер тізімінен тұрады.

Кіріспеде дипломдық жұмыс тақырыбының өзектілігі және мақсаты туралы қысқаша оның құрылымы және мазмұны туралы айтылған.

Бірінші тарау компьютер көмегімен есеп шығару технологиясы ерекшелігі және модельдеудің, сандық әдістердің осы технологиядағы алатын орнына және маңызы туралы мәселелерге арналған.

Екінші тарауда негізінен модельдеу және есепті шешу әдістерін әртүрлі практикалық есептерді шешуде пайдаланудың тәсілдері, осы модельдеу және есепті шешу әдістері арасындағы байланысты оқушылардың математикалық білімдері, біліктілігін деңгейлерін тереңдетуде тиімді пайдалану мәселелері туралы автор ой-пікірі қарастырылған.

Қорытыңдыда осы диплом жұмысындағы ойларды, тәсілдерді, ұсыныстарды мектеп математика курсын оқытуда тиімді түрде пайдалануға болатыңдығы туралы кеңес берілген.

Автор диплом жұмысын орындау барысында көптеген әдебиеттерге оның ішінде ғылыми-әдістемелік журналдарға да («Математика», «Математика в школе», «Информатика негіздері», «Информатика и образование») сараптаулар жүргізді, оңдағы осы бағыттағы мақалалар және материалдармен танысты. Ол әдебиеттердің негізгілері диплом жұмысындағы тізімге еңгізілді.

ДӘЙЕКТЕМЕ

Дипломдық жұмыста оқушылардың математикалық білімі мен біліктілігі деңгейлерін жақсартуда математикалық модельдеу және сандық әдістер арасындағы байланысты пайдалану идеялары қарастырылған.

АННОТАЦИЯ

В дипломой работе рассматриваются вопросы использования связи математического моделирования и численных методов для улучшения уровня знаний и умений учащихся по математике

АNNOTATION

The using of Linking of mathematic model and numeral methods of improving on the Level of knowledge and skills of students according mathematic are considered in this diploma project.

Бірінші тарау

Модельдеу және сандық әдістер

Модельдеу және сандық әдістер туралы

Бүгінгі күні кез-келген пайдаланушы өз мамаңдығын тиімді іске асыруда компьютерді пайдаланады. Тікелей компьютерді пайдалану кезінде негізінен дайын қолданбалы программаларға (Excel, Mathcad, Avtokad, т. с. с. ) жүгінеді.

Ал енді, өмірде кездесетін есептердің барлығы сол дайын программалар көмегімен тиімді шешіле бермейді. Сондықтан болашақ маман дайын қолданбалы программалармен қатар компьютер көмегімен өзі де жаңа өзіңдік программалар жаза, дайындай алатын болса, өз саласына байланысты жаңа есептерді тұжырымдай қоя білсе нұр үстіне нұр болар еді.

Қазіргі заманғы жоғарғы және арнаулы орта оқу орындары ақпараттық технологияларды кез-келген жағдайда өз саласында тиімді пайдаланыла алатын мамандар дайындаулары керек. Ал ондай мамандар компьютер көмегімен математикалық есептерді де шеше білу тиіс болады.

Мысалы, физиктерді немесе инженерлерді математика әйтеуір математика ретінде қызықтырмайды, оларға математика физикалық немесе техникалық есептерді шешу құралы ретінде керек.

Мысалы, жаңа бір зат, құрал-жабдық жасау немесе завод-фабрика салу керек болатын болса, реальді есептерді шешуге тура келеді. Есептеу жүргізудің мақсаты - тиімділікті анықтау. Тиімді шешімді анықтаудың жолы, тәсілі, әдісі әртүрлі болады.

Мысалы, сондай тәсілдің бірі эксперимент, эксперимент жүргізгенде, мысалы, лампаны жасайды, немесе химиялық жабдықты құрайды, немесе заводтың алғашқы нұсқасын салады, содан кейін барып, бізге қажетті көрсеткіштерді өлшейді, тіркейді және жинайды. Егер де жасаған затымыз, жабдығымыз, немесе салған зауытымыз тиімді болмай шықса, онда оларға нақты өзгерістер енгіземіз, немесе қайта жасаймыз, саламыз, т. с. с.

Осындай іс-әрекеттер нәтижесінде тиімді нұсқаға жетуіміз мүмкін, бірақ та бұл жол (тәсіл) шыли қымбатқа түседі және көп уақытты алатын болады.

Қымбатқа түсетін, көп уақытты алатын және өмірге қауіп төндіретін жағдайларды жеңілдетудің, арзандатудың, тиімді етудің бір жолы - ол конструкцияның немесе құбылыстың, процестің моделін, оның ішінде негізінен математикалық моделін қарастыру болып табылады. Бұл жағдайда математикалық талдаулар тікелей реальді құбылысқа емес, оны алмастыратын кейбір математикалық модельге жүргізілетін болады. Сондықтан мұндай жағдайда бірінші кезекте есептің қойылуы және оның математикалық моделі қарастырылады.

Мысалы, физикалық процеске арналған модель осы процесті сипаттайтын теңдеулерден тұрады. Бұл теңдеулерге процеске қатысушы дене немесе зат көрсеткіштері коэффициенттер түрінде енеді.

Мысалы, вакуумде вертикаль бағытта ұшатын ракетаның жылдамдығы

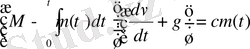(1. 1. 1)

теңдеуімен анықталады. Мұндағы М - ракетаның бастапқы массасы ; m(t) - берілген жанармай шығыны (жұмсалатын жанармай көлемі) ; g - тартылу өрісінің үдеуі; с - газдың шығу жылдамдығы (уақыты), ол жанармай калорийлығына және жанатын заттың орташа малекулярлық салмағына тәуелді болады. Кез келген зерттелінетін, қарастырылатын құбылыс өте күрделі болады. Олар табиғаттың басқа да құбылыстарымен байланысқан, байланыста болуы мүмкін. Мүмкін, олар қарастырып отырған есеп жағдайында бізді қызықтырмауы да. Математикалық модель осы құбылыстың, қарастырып отырған жағдайдағы ең басты, ол құбылыстың іске асуына шешуші әсер ететін параметрлердің (көрсеткіштері жақтарын) ғана қамтуы тиіс.

Есептің қойылуы кезіндегі күрделі және жауапты жұмыс - ол құбылыстың, процестің, объектінің қарастырып отырған есеп жағдайындағы негізгі маңызды көрсеткіштерін және олардың арасындағы байланыстарын формализациялауда және модельдеуде таңдау және пайдалану болып табылады.

Егерде есептің математикалық моделі дұрыстап ұқыпты таңдалынбаған болса, қандай да тиімді есептеу әдісін қолдансақтағы жақсы нәтижеге жету қиын, ал тіпті кейбір жағдайларда мүмкін болмайтын болады. Мысалы (1. 1. 1) теңдеуі жер бетінен ракета жіберуге жарамайды, себебі - онда ауаның кедергісі ескерілмеген.

Сондықтан, бұл бағыттығы жұмыстың келесі кезеңі - математикалық зерттеу жүргізу болып табылады. Модельдің күрделік деңгейіне сәйкес әртүрлі математикалық тәсілдер қолданылады. Қарапайым және онша күрделі емес модельдер үшін аналитикалық шешімдерді алуға мүмкіндіктер болады. Бұл жолды/тәсілді негізінен физик-теоретиктер жиі қолданады, пайдаланады. Мысалы, (1. 1. 1) теңдеуі g=const және m=const болғанда оңай интегралданады:

v=c ln [M/(M-mt) ] -gt. (1. 1. 2)

Мұндай жағдайда модельдің шыли қарапайымдылығынан бұл тәсілдің физикалық дәлдігі өте төмен болады. Көп жағдайларда мұндай тәсіл шамалар ретін бағалауға ғана мүмкіндік береді.

Жалпы, дәлірек және күрделі модельдер үшін шешімдерді аналитикалық түрде алу және табу өте сирек кездесетін жағдай. Теоретиктер негізінен қанағаттанарлық сапалық және сандық нәтижелерді алуға мүмкіндік беретін жуықтау математикалық әдістерді (мысалы, кіші параметр бойынша жіктеу) қолданады. Ал енді тіпті күрделі және дәлірек модельдерді шешуде негізінен сандық әдістерді пайдаланады. Сандық әдістер бойынша есептеулерді тиімді жүргізу үшін компьютер пайдаланылады. Сандық әдістер зерттелетін құбылыстарды, процестерді сапалы өңдеумен қатар сандық жағынан да жеткілікті деңгейде сипаттауға мүмкіндік береді. Барлық жағдайда да шешімнің математикалық дәлдігі модельдің физикалық дәлдігімен салыстырғанда 2-4 есе жоғары болуы тиіс. Шыли төмен математикалық дәлдікті ( практика жүзінде есепті шығаруды жеңілдету үшін кейбірде қосымша математикалық қарапайымдатулар орын алатыны болады) жіберуге болмайды, ондай жағдайларда нәтижелердің құндылығы (артықшылығы, ерекшелігі) төмендейді.

Осы бағыттағы жұмыстың келесі кезеңінде - математикалық шешімге талдау жүргізеді, оны эксперименттік берілгендермен салыстырып көреді. Егерде математикалық есептеулер және нәтижелер эксперименттік мәліметтермен/берілгендермен үйлесетін болса, онда математикалық модель дұрыс таңдалынған деп есептелінеді және бұл модельді осы типтес процестерді/есептерді шешуде пайдалануға болады деген қорытындыға келуге болады.

Ал егерде математикалық есептеулер нәтижесі және эксперимент сәйкес келмейтін/үйлеспейтін болса, онда модельді қайта қарау (оның параметрлеріне сараптау жүргізу) керек болады.

Сандық әдістер. Сандық әдістер математикалық есептерді шешудің негізгі қуатты құралы болып табылады. Қарапайым сандық әдістерді біз күнделікті пайдаланамыз. Мысалы, қарапайым сызықты немесе квадрат теңдеуді шешуді, квадрат түбір табуды жиі қолданамыз. Бірақта, өмірде кездесетін есептердің барлығы қарапайым бола бермейді, ондай жағдайларда арнаулы сандық әдістерді пайдалануға тура келетін болады, онсыз күрделі есеп шешімін табу мүмкін болмайды. Мысалы, мына классикалық есепті еске түсіруге болады -Нептунның ашылуы Урандағы қозғалыс аномалиялары бойынша ғана мүмкін еді.

Ал мұндай есептер қазіргі заманғы физикада көптеп кездеседі. Мұндай есептерде қысқа мерзімде өте көп үлкен, күрделі есептеулерді жүргізуге тура келеді, жауап тез арада алынбаса есеп нәтижесі өз мағынасын жоғалтады, керек болмай қалады. Мысалы, ауа райының тәуліктік болжамы бірнеше сағат бұрын ғана есептелінуі керек, ракетаның траекториясына енгізілетін коррекцияны бірнеше минутта есептеп қою керек болады; прокаттық стан жұмысы режимі бір секунд ішінде шешілуі керек. Ал мұндай есептеулерді қуатты компьютерлерсіз жүргізу мүмкін емес.

Қазіргі заманғы сандық әдістер және қуатты ЭЕМ-дер осыдан бір жарты ғасыр бұрын арман болып келген күрдел есептерді шешуге мүмкіндік беріп отыр. Сондықтан сандық әдістерді тиімді пайдалану мәселесі де бүгінгі күннің өзекті мәселелерінің біріне айналып отыр. Мысалы, ЭЕМ тек арифметикалық және логикалық амалдарды ғана орындай біледі.

Сондықтан кез келген практикалық есепті компьютер көмегімен шешу үшін алдымен оның математикалық моделін құрады, одан кейін барып таңдалынған тиімді сандық әдістер негізінде оның шешудің алгоритмін жазады, яғни ЭЕМ-ге орындалатын арифметикалық және логикалық амалдардың тізбегі көрсетіледі.

Модель және алгоритмді ЭЕМ-нің қуаттылығына (оперативтік жадының көлеміне және жылдамдығына) сәйкес тандайды. Өйткені, шыли күрделі модельді орындауға машинаның қуаты жетпеуі мүмкін, ал шыли қарапайым модель қанағаттанарлық шешім алуға мүмкіндік бермейді.

ЭЕМ-ге арнап дайындалынатын алгоритм де және программа да ұқыпты тексеріліп жазылуы тиіс. Программаны тексеру және оны тестілеуден өткізу де оңай проблема емес. Өйткені, мәселенің көбісі таңдалынған сандық әдістерге және құрылған алгоритмнің сапалық деңгейіне тәуелді болады. Ал таңдалынатын сандық әдіс және алгоритм сапасы математикалық модель деңгейіне көп байланысты болады. Модельдің қойылатын талаптарға толығырақ жауап беруі эксперименттік берілгендер және нәтижелермен тексеріледі.

Алгоритмнің қатаң математикалық негізделінуі зерттеудің соңғы, аяқты нәтижесі болып шығуы сирек жағдай болып келеді. Мысалы, итерациялық процестердің жинақтылығын дәлелдеудің көбісінің дұрыстығы барлық есептеулер қатаң ережеге сай жүргізілгенде ғана орын алуы мүмкін. Өйткені, практикалық есептеулерде ондық бөлшек таңбаларын көбірек етіп сақтау үлкен проблема (мысалы, қолмен есептегенде 5-6 таңбаны сақтау, ал ЭЕМ-де есептегенде 10-12 таңбаны сақтаудың өзі сирек жағдай) . Тіпті алгоритмнің кейбір майда-шүйде мәселелерінің өзін теориялық тұрғыда негіздеу немесе дәлелдеу үлкен проблемаға айналуы мүмкін. Сондықтан, көп жағдайларда сандық әдістердің тиімділігіне баға беру тек практикалық (эксперименттік) нәтижелерден кейін ғана мүмкін болады.

Мысалы, күрделі есептерді шешуге арналған сандық әдістерді дайындау, негіздеу және ЭЕМ-ге арнап программа жазу өте үлкен күрделі жұмысқа айналуы мүмкін, тіпті бұл жұмыс бірнеше айдан бірнеше жылдарға дейін де созылатын жағдайлар кездеседі. Кейбірде, жақсылап тексерілген, жоғары деңгейдегі күрделі проблемалар кешенін дайындауға кететін қаржының көлемі экспериментальді түрде жасалынған физикалық құрылғы, жабдыққа жұмсалатын қаржымен шамалас болуы да мүмкін. Дегенмен, мұндай кешен бойынша қайталап есептеу жүргізулер жеке бөлек эксперимент жүргізуден әлдеқайда арзанға түседі және жылдам жүргізілетін болады. Сондықтан, мұндай программалар кешені зерттеліп отырған конструкцияның оптимальді параметрлерін тиімді түрде жылдам таңдауға мүмкіндік береді.

Әрине, бұл жерде мына жағдайды атап айтуымыз керек - сандық әдістер барлық мәселелерді толық шешуге мүмкіндік бере бермейді. Сондықтан басқа да қарапайым математикалық әдістерді де пайдалана білуіміз керек болады. Мысалы, зерттеудің бастапқы кезеңінде қарастырып отырған проблеманы зерттеуде қарапайым модельдерді, аналитикалық әдістерді және шамалап есептеулерді де пайдаланған жөн болар еді. Қарастырып отырған проблеманың мазмұнын және күрделік деңгейін анықтап алғаннан кейін барып қана, күрделі толық модельдерге және сандық әдстерді пайдалануға көшу керек. Тіпті бұл жағдайлардың өзінде де оларды сандық әдістермен үйлестіре пайдаланған тиімді болады.

Сонымен, қазіргі заманғы физик, химик, биолог, инженер, технолог, экономист және басқада ғылым мамандары өз саласының жоғары деңгейдегі кәсіпқой маманы болуы үшін математиканың «классикалық» әдістерін де және сандық әдістерін де жақсы меңгергендері тиімді болар еді.

Математиканың ғылымның әртүрлі салаларының күрделі есептерін шешуге арналған сандық алгоритмдерді дайындаумен және негіздеумен айналысатын тарауын қолданбалы математика деп атайды. Қолданбалы математиканың басты міндеті - шешімді іс жүзінде талап етілетін дәлдік бойынша табу. Қолданбалы математиканың классикалық математикадан айырмашылығы осында, яғни классикалық математика негізгі назарды шешімнің бар болу шарттарына және шешімнің қасиеттерін зерттеуге бағыттайды. Бұл деген сөз - жақсы сауатты математик болу үшін және математиканы кез келген салада тиімді пайдалана білу үшін классикалық математикадан да және компьютер көмегімен математикалық есептерді шешу технологиясынан да (модельдеуден, сандық әдістерден, алгеритмдеу негіздерінен) жеткілікті деңгейде дайындық болғаны жөн.

1. 2. Компьютер көмегімен математикалық

есептерді шығару технологиясы туралы

Есепті компьютер көмегімен шығаруға дайындау және шығару технологиясын түсіну және оны меңгеру, кезкелген практикалық есептерді шешуде компьютерді тиімді пайдалануға толық мүмкіндік береді.

Кез келген салада, ғылымда және техникада ақпараттық технологияларды мақсатты және тиімді пайдалану деңгейі, инновациялық жүйелердің дұрыс қалыптасуы өмірде кездесетін практикалық есептерді (тапсырыстарды) ғылыми тұрғыда сауатты қоюға және оны шешудің технологиясын (тәсілдерін) меңгеруге тікелей байланысты болады.

Кез келген келешек маман біз көрсетіп отырған осы технологияны меңгеруі және пайдалана білуі керек, өйткені ол ақпараттандырылған қоғамда өмір сүріп және қызмет ететін болғандықтан, осы қоғамды құруға және дамытуға белсене араласуы тиіс болады.

Келешектің кез келген маманы компьютерді өз жұмысында тиімді пайдаланғысы келсе, онда ол өз саласы бойынша алға қойылатын проблемаларды тұжырымдай алуы (яғни, өз саласын, мамандығын жақсы білетін) және оны компьютер көмегімен шығара алатын болуы тиіс. Сондықтан ол тікелей кезкелген есепті (жұмысты, тапсырманы) қоюды және оны компьютер көмегімен шығаруды (өңдеуді, орындауды) жете меңгеруі қажет. Біздің қарастыратын мәселеміз кез келген маман-пайдаланушы (ақпараттық технологиялар негіздерімен қатар) үйренуге және білуге тиісті стандартты (міндетті) жағдайлар болмақшы.

Жалпы, компьютер көмегімен кез келген есепті шешу (ақпаратты өңдеу, қойылған жұмысты орындау) мына төмендегі бір-бірінен тәуелсіз (әр кезеңді автономды, аяқталынған, жекелеп қарастыруға болады деген мағынада), бірақта бір-бірімен логикалық байланысқан кезеңдерден тұрады:

- е септің (жұмыстың, тапсырманың) қойылуы;

- есептің моделін құру;

- есепті шешудің тиімді әдісін (тәсілін, жолын) таңдау;

- есепті шығарудың алгоритмін құру;

- есепті шығарудың программасын жазу;

- программаның қатесін анықтау және оны жөндеу, программаны тестілеуден өткізу;

- есепті тікелей компьютерде шығару;

- алынған нәтижеге талдау жүргізу.

Осы көрсетілген әрбір кезеңнің нақты мақсаты және міндеті анықталған. Енді соларға жеке-жеке тоқталайық.

1. 2. 1. Есептің (жұмыстың, тапсырманың) қойылуы.

Жалпы, есептің қойылуы мына жағдайларды қамтиды:

а) қойылған есептің мазмұнын және оның ерекшелігін түсіну;

б) осы есепке қажетті негізгі ақпаратты жинақтау;

в) жиналған ақпарат негізінде есептің мазмұнын қысқаша тұжырымдау;

г) есепке талдау жүргізу. Талдау жүргізудің мақсаты:

г1) нақты тұжырымдалған есеп мазмұнын жақсы түсіну;

г2) бастапқы берілгендерді (яғни, компьютер жадына бірінші кезекте енгізілетін мәліметтерді) анықтау;

г3) аралық шамаларды және нәтижелерді анықтау (есептеуді тиімді ұйымдастыруға және компьютер жадын тиімді пайдалануға байланысты қажет болатындықтан) ;

г4) есептің шешімінің (яғни, соңғы нәтижелердің) нелер болатындығын анықтау;

г5) қандай шарттардың орындалуында есептің нақты шешімдері болатындығын анықтау;

г6) шешімді қандай формада және форматта алуды анықтау (көрсету) .

Осы келтірілген тұжырымдаулардан, бұл бірінші кезеңнің компьютер көмегімен есеп шығарудың ең басты және жауапты кезеңі екендігін байқауымызға болады. Өйткені, есептің тиімді жолмен (әдіспен, тәсілмен) шешілуі көп жағдайда есептің дұрыс және ғылыми-теориялық тұрғыда сауатты қойылуына тікелей байланысты болып келеді.

1. 2. 2 . Есеп моделін құру.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.