Сәуленің кванттық табиғаты

Пән: Физика
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 56 бет
Таңдаулыға:

Мазмұны

I тарау. Сәуленің кванттық табиғаты . . . 5

§1. Жылулық сәулелену және оның сипаттамасы . . . 5

§1. 2 Кирхгоф заңы . . . 6

§1. 3 Стефан - Больцман және Виннің ығысу заңы . . . 7

§1. 4 Релей - Джинс және Планк формулалары . . . 8

§1. 5 Оптикалық пирометрия . . . 11

§1. 6 Жарықтың жылулық көздері . . . 12

§1. 7 Фотоэффект . . . 12

§1. 7. 1 Фотоэлектрлік эффект түрлері. Сыртқы фотоэффект заңдары . . . 12

§1. 7. 2 Сыртқы фотоэффект үшін Эйнштейн теңдеуі. Жарықтың кванттық қасиетінің эксперименталдық дәлелдемесі . . . 15

§1. 7. 3 Фотоэффекттің қолданылуы . . . 17

§1. 8 Фотон массасы және импульсі. Жарық қысымы . . . 18

§1. 9 Комптон эффекті және оның элементар теориясы . . . 19

II тарау. Бор теориясы бойынша сутегі атомы . . . 20

§2. 1 Атомның Томсон және Резерфорд моделі . . . 20

§2. 2 Сутек атомының сызықты спектрлері . . . 21

§2. 3. Бор постулаттары . . . 22

§2. 4 Франк және Герц тәжірибесі . . . 23

§2. 5 Сутегі атомы спектрлерін Бор теориясы бойынша түсіндіру . . . 24

III тарау. Кванттық механиканың негіздері . . . 25

§3. 1 Заттардың корпускулалық - толқындық теориясы. ., . . . 25

§3. 2 Анықталмаушылық қатынастар . . . 26

§3. 3 Толқындық функция және оның статистикалық мағынасы . . . 27

§3. 4 Шредингер теңдеуі. Стационар күйдегі Шредингер теңдеуі . . . 28

§3. 5 Кванттық механикадағы себеп - салдар принципі . . . 30

§3. 6 Еркін бөлшектің қоғалысы . . . 30

§3. 7 Тік бұрышты потенциалдық «шұңқырдағы» бөлшек қоғалысы . . . 31

§3. 8 Бөлшектің потенциалдық бөгеттен өтуі. Туннельдік эффект . . . 33

§3. 9 Кванттық механикадағы сызықты гормоникалық осцилятор . . . 35

IV тарау. Қазіргі атомдық физика негіздері . . . 37

§4. 1 Кванттық механикадағы сутегі атомы . . . 37

§4. 2 Сутегі атомындағы электронның 1 s- күйі . . . 40

§4. 3 Электрон спині. Спиндік кванттық сан . . . 42

§4. 4 Тепе - тең бөлшектерді ажырата алмаушылық принципі . . . 42

§4. 5 Паули принципі. Атомда электрондардың күй

бойынша орналасуы . . . 44

§4. 6 Менделеевтің элементтер периодтық жүйесі . . . 45

§4. 7 Рентген спектрлері . . . 47

V тарау. Қазіргі молекулалар физикасының элементтері . . . 49

§5. 1 Молекулалар: химиялық байланыстары, энергетикалық деңгейлері

жөнінде түсінік . . . 49

§5. 2Молекулалықспектрлер. . . . 51

VI тарау. Лазерлік физика негіздері . . . 53

§6. 1 Жұтылу. Спонтанды және мәжбүрлі сәулелену . . . 53

§6. 2 Оптикалық кванттық генераторлар (Лазерлер) . . . 54

Пайдаланылған әдебиеттер . . . 58

I тарау. Сәулеленудің кванттық табиғаты

Жылулық сәулелену және оның сипаттамасы

Жеткілікті жоғары температурада қыздырылған дене жарқырайды. Қыздыру арқылы дененің жарқырауы жылулық сәулелену деп аталады. Жылулық сәулелену табиғатта ең кең таралған. Ол - заттың молекулалары және атомдарының жылулық қозғалыс энергия (яғни, ішкі энергия) есебінен және сәйкесінше барлық денелер үшін 0 К - нен жоғары температураларда орындалады. Жылулық сәулелену максимумы температураға тәуелді болатын тұтас спектрмен сипатталады. Жоғарғы температурада қысқа (көрінетін және ультракүлгін) электромагниттік толқын, ал төменгі температурада ұзын (инфрақызыл) электромагниттік толқын шығады.

Жылулық сәулелену - тепе-теңдікті болатын жалғыз сәулеленудің түрі. Қыздырылған дене сырты шағылдырғыш қабықпен қапталған қуыста орналасты дейік. Біршама уақыттан соң дене мен сәуле арасында үздіксіз энергия алмасуынан кейін тепе-теңдік орнайды, яғни дене бірлік уақытта қанша энергия шығарса, сонша энергия жұтылады. Дене мен сәуле арасындағы тепе-теңдік белгілі себептермен бұзылды және дене жұтылуға қарағанда көп энергия шығарады делік. Егер дене бірлік уақытта жұтылуға қарағанда көп энергия шығарса (немесе керісінше), онда температурасы төмендейді (немесе жоғарылайды) . Басқа сәулелену түрлері тепе-теңдікті емес.

Жылулық сәулеленудің сандық сипаттамасы үшін жиіліктің бірлік ұзындықты интервалында дене бетінің бірлік ауданындағы сәулелену қуаты - дененің энергиялық жарқырауының спектрлік тығыздығы алынады

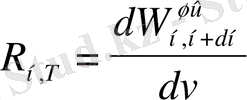
мұнда 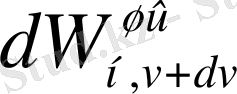- жиіліктің ν және dν интервалында дене бетінің бірлік ауданынан бірлік уақытта шығарылатын электромагниттік сәулелену энергиясы.

Энергетикалық жарқыраудың спектрлік тығыздығы өлшем бірлігі [ R _{v, T} ] =[ Дж/м ² ] .

Формуланы толқын ұзындығы түрінде де көрсетуге болады: , 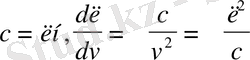болады, минус ν немесе λ шамаларының біреуі өскен кезде екіншісі төмендейтінін көрсетеді. Сондықтан минус таңбасын қалдырып жазуға болады.

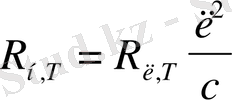(1. 1)

Энергетикалық жарқыраудың спектрлік тығыздығын біле отырып, интегралдық энергетикалық жарқырауды есептеуге болады:

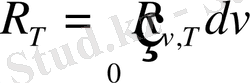(1. 2)

Дененің түскен сәулені жұту қабылеті спектрлік жұту қабылетімен сипатталады: 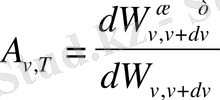. Формула дене бетінің бірлік ауданына бірлік уақытта түсірілген жиілігі ν және dν аралығындағы электромагниттік толқын әкелетін қанша энергия мөлшерін дененің жұтатынын көрсетеді. Спектрлік жұту қабылеті - өлшемсіз шама. R _{v, T} және A _{v, T} шамалары дене табиғатына, оның термодинамикалық температурасына тәуелді және әр түрлі жиілікті сәулелер үшін ажыратылады. Сондықтан бұл шамалар белгілі Т және ν шамаларына қатысты болады.

Кез келген температурада кез келген жиілікті сәулелерді толығымен жұтуға қабылетті денелерді абсолют қара дене деп атайды. Барлық жиіліктер және температуралар үшін қара дененің спектрлік жұту қабылеті бірге тең ( 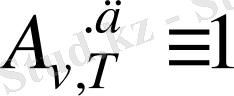) . Абсолют қара дене табиғатта кездеспейді, бірақ қара күйе, қарайтылған платина, қара барқыт және басқалары сияқты денелер белгілі жиілік интервалында қасиеттерімен абсолют қара денеге ұқсас келеді.

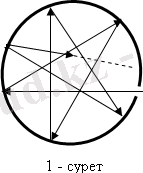
Қара дене моделі үшін О кішкене тесігі бар, ішкі беті қарайтылған тұйық қуысты аламыз (1-сурет) . Қуыстың ішіне енген жарық сәулесі қабырғадан көп шағылады. Нәтижесінде шыққан сәуленің интенсивтілігі нөлге тең болады. Егер тесік өлшемі қуыстың диаметрінің 0, 1 бөлігінен де кішкентай болғанда кез келген жиілікті түскен сәуле толығымен жұтылатынын тәжірибе көрсетті.

Қара дене түсінігімен қатар сұр дене түсінігі қолданылады. Бұл дененің жұту қабылеті 1-ден кіші және кез келген жиілік үшін бірдей болады және тек температураға, материалға, дене бетінің күйіне байланысты. Сұр дене үшін .

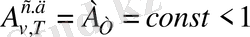Жылулық сәулеленуді зерттеу жарықтың кванттық теориясының пайда болуында маңызды роль атқарды, сондықтан ол бағынбайтын заңдарды міндетті түрде қарастыру керек.

Кирхгоф заңы

Неміс физигі Г. Кирхгоф термодинамиканың 2-ші заңына сүйеніп және изоляцияланған жүйедегі дененің тепе-теңдік сәулелену шарттарын ескере отырып, энергетикалық жарқыраудың спектрлік тығыздығы және спектрлік жұту қабылеті шамаларының арасында сандық байланыс орнатты. Кирхгоф заңы: энергетикалық жарқыраудың спектрлік тығыздығының спектрлік жұту қабылетіне қатынасы дененің табиғатына байланысты емес; ол барлық денелер үшін жиілік пен температураның универсалды функциясы болып табылады: 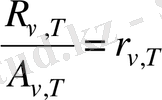(1. 3)

Қара дене үшін 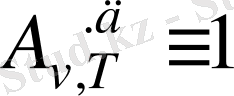, сондықтан Кирхгоф заңынан (1. 3) қара дене үшін R _{v, T} =r _{v, T} шығады. Кирхгофтың универсал функциясы r _{v, T} - қара дененің энергетикалық жарқырауының спектрлік тығыздығы болып табылады. Кирхгоф заңына сәйкес барлық денелер үшін спкетрлік тығыздықтың спектрлік жұту қабылетіне қатынасы қара дененің сол температурады және жиіліктегі энергетикалық жарқырауының спектрлік тығыздығына тең.

Кирхгоф заңынан барлық кез келген дененің кез келген спектрлік облысындағы энергетикалық жарқырауының спектрлік тығыздығы әрқашан қара дененің энергетикалық жарқырауының спектрлік тығыздығынан кіші болады, А _{v, T} <1 болғандықтан R _{v, T<} r _{v, T} екені келіп шығады. Сонымен қатар, (1. 3) теңдігіне сәйкес, егер дене берілген температура Т , жиілік интервалы ν және dν аралығындағы электромагниттік толқындарды жұтпаса, онда ол осы жиілік интервалында Т температурада А _{v, T} =0, R _{v, T} =0 болғандықтан сәуле шығармайтыны келіп шығады.

Кирхгоф заңын қолдана отырып, дененің энергетикалық жарқырауы (1. 2) теңдігін былай жазуға болады.

Ал сұр дене үшін 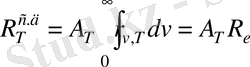(1. 4)

мұнда R _e - қара дененің энергетикалық жарқырауы (тек температураға тәуелді)

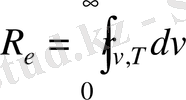(1. 5)

Кирхгоф заңы тек жылулық сәулеленуді сипаттайды, бұл заңға бағынбайтын сәулеленулер жылулық деп аталмайды.

Стефан - Больцман және Виннің ығысу заңы

Кирхгоф заңынан (1. 3) қара дененің энергетикалық жарқырауының спектрлік тығыздығы универсал функция екені белгілі. Сондықтан оның жиілікке және температураға тәуелділігі жылулық сәулелену теориясының маңызды есебі болып табылады.

Австриялық физик Я. Стефан эксперимент нәтижелерін сараптай отырып (1879 ж) және австриялық физик Л. Болцман термодинамикалық әдісті қолданып (1884 ж), энергетикалық жарқыраудың R _e температураға тәуелділігін енгізе отырып бұл есепті жартылай шешті. Стефан - Больцман заңына сәйкес 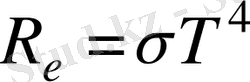, (1. 6)

яғни энергетикалық жарқырау қара дененің термодинамикалық температурасының төртінші дәрежесіне пропорционал. Мұнда σ - Стефан - Больцман тұрақтысы, оның эксперименттік мәні 5, 67 *10 ^-8 Вт /( м ² К ⁴ ) .

Стефан - Больцман заңы R _e -нің температураға тәуелділігін анықтай отырып, қара дененің сәулеленуінің спектрлік құрамына қатысты жауап бермейді. Эксперименталдық қисықтардан әр түрлі температураларда r _{v, T} -дің толқын ұзындығына 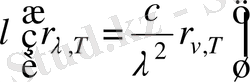тәуелділік графигінен қара дене спектрінде энергияның таралуы бірдей өлшемді емес екені байқалады (2-сурет) .

Барлық қисықтар температура өсуімен қысқарақ толқындарға қарай ығысатын анық максимумдардан тұрады. r _{v, T} -дің λ -ға тәуелділігіндегі қисықпен және абсцисса осімен шектелген аудан қара дененің энергетикалық жарқырауына R _e және Стефан - Больцман заңы бойынша температураның төртінші дәрежесіне пропорционал.

Неміс физигі В. Вин термо және электродинамика заңдарына сүйеніп, r _{v, T} функциясының максимумына сәйкес келетін толқын ұзындығының λ _тах температураға Т тәуелділігін енгізді. Виннің ығысу заңына сәйкес 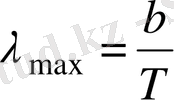, (1. 7)

яғни қара дененің энергетикалық жарқырауының спектрлік тығыздығының r _{v, T} максимал мәніне сәйкес келетін толқын ұзындығы λ _тах оның термодинамикалық температурасына кері пропорционал. Мұнда b - Вин тұрақтысы, оның эксперименттік мәні 2, 9*10 ^-8 мК . Осыдан (1. 7) көрінісі Виннің ығысу заңы деп аталады, ол r _{v, T} функциясының максимум күйінің температура көтерілуімен қысқа ұзындықты толқындар аймағына ығысатынын көрсетеді. Вин заңы неліктен қыздырылған денелердің температурасын төмендеткенде олардың спектрінде толқын ұзындығы үлкен сәулелер көбейетіндігін түсіндіреді.

Релей - Джинс және Планк формулалары

Стефан - Больцман және Вин заңдарын қарастыру негізінде Кирхгофтың универсал функция r _{v, T} жөніндегі есебін термодинамикалық жолмен шешу күткен нәтижелерді бермеді. Келесі r _{v, T} - ға қатысты теориялық тұжырым, энергияның еркіндік дәрежесі бойынша бірдей таралуы классикалық заңына сәйкес статикалық физика әдістерін жылулық сәулеленуге қолданған ағылшын ғалымдары Д. Рэлей және Д. Джинске тиісті.

Энергетикалық жарқырауының спектрлік тығыздығы үшін Рэлей - Джинс формуласы 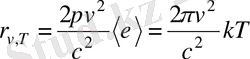(1. 8)

Мұнда 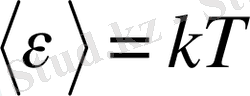- меншікті жиілікті осцилятордың орташа энергиясы, к =1, 38*10 ^-23 Дж/К - Больцман тұрақтысы. Тербелмелі осцилятор үшін кинетикалық және потенциалдық энергияларының орташа мәні бірдей, сондықтан әрбір тербелмелі еркіндік дәреженің орташа энергиясы .

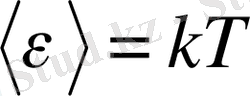Тәжірибе көрсеткендей (1. 8) көрінісі эксперимент нәтижелеріне тек жеткілікті кіші жиілікте және жоғары температурада сәйкес келеді. Жиіліктің жоғары аймақтарында Рэлей - Джинс формуласы эксперименттен және Виннің ығысу заңынан алшақтап кетеді (3-сурет) . Сонымен қатар, Рэлей - Джинс формуласынан Стефан - Больцман заңын алу мағынасыздыққа алып келеді. Шынында да, (1. 8) -ді қолданып есептелген қара дененің энергетикалық жарқырауы (1. 5)

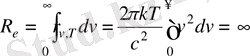онда Стефан - Больцман (1. 6) заңына сәйкес бұл температураның төртінші дәрежесіне пропорционал. Бұл нәтиже «ультракүлгіндік апат» деген атқа ие болды. Осылай классикалық физика арқылы қара дене спектрінде энергияның таралу заңын түсіндіру мүмкін болмады.

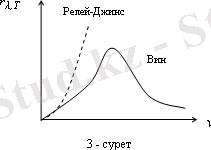
Жоғары жиілікті аймақта Вин формуласы тәжірибемен үйлесім табады.

мұнда r _{v, T} - қара дененің энергетикалық жарқырауының спектрлік тығыздығы, А және С - тұрақты шамалар. Планк тұрақтысын қолдана отырып Виннің сәулелену заңын былай жазуға болады.

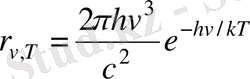
Қара дененің энергетикалық жарқырауының спектрлік тығыздығы үшін тәжірибе нәтижелеріне толық сәйкес келетін теңдеуді 1900 ж Планк анықтады. Бұл үшін оған классикалық физикада бекітілген жағдайдан бас тартуға тура келді. Ол жағдай бойынша кез келген жүйенің энергиясы үздіксіз өзгере алады, яғни кез келген көптеген жақын мәндерді қабылдай алады. Планктың бұл кванттық гипотезасына сәйкес атомдық осциляторлар энергияны үздіксіз шығармайды, белгілі порциямен - кванттар шығарады. Энергия кванты тербеліс жиілігіне пропорционал

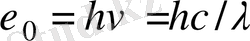(1. 9)

мұнда h= 6. 65*10 ^-34 Дж*с - Планк тұрақтысы . Сәуле порция түрінде шығарылатындықтан осцилятор энергиясы тек белгілі дискретті мәндерді қабылдайды: ε=nhv, n - бүтін сан.

Бұл жағдай үшін осцилятордың орташа энергиясын 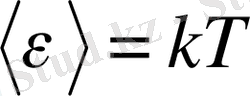деп алуға болмайды. Осцилятордың мүмкін болған дискретті күйлері бойынша таралуы Больцманның таралуына бағынады. Осцилятордың орташа энергиясы мынаған тең: ,

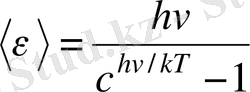ал қара дене энергетикалық жарқырауының спектрлік тығыздығы

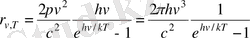Осылай Планк Кирхгофтың универсал функциясы үшін

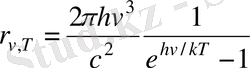(1. 10)

эксперимент нәтижелеріне анық сай келетін формуланы шығарды. Бұл формуланың теориялық тұжырымын М. Планк 1900 ж 14 желтоқсанда неміс физиктер қоғамы мәжілісінде баяндады. Бұл күн кванттық физиканың туған күні есептелді.

Төмен жиілікті аймақта, яғни hv<<kT (энергия кванты жылулық қозғалыс энергиясына қарағанда әлдеқайда кіші) кезінде Планк формуласы Рэлей - Джинс формуласымен (1. 8) сәйкес келеді. Қарастырылып отырған жағдайда алғашқы екі мүше үшін мынаны аламыз .

Бұны Планк формуласына (1. 10) қойсақ, Рэлей - Джинс формуласы шығады.

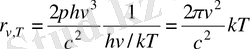
Планк формуласынан Стефан - Больцман заңын алуға болады. (1. 5) және (1. 10) сәйкес

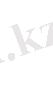
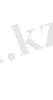
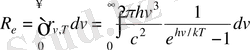
Айнымалыларды енгіземіз x=hv/kT; dx=hdv/kT; dv=kTdx/h. R _e үшін формула мына түрге келеді. 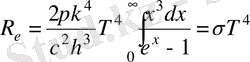(1. 11)

мұнда 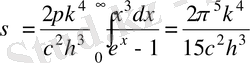, ал .

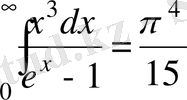Сонымен қатар, к, с және сандық мәндерін бере отырып, Стефан - Больцманның экспериментпен сәйкес келетін тұрақтысының мәнін алуға болады. Виннің ығысу заңын (1. 1) және (1. 10) формулаларға сүйене отырып аламыз.

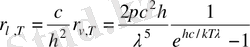бұдан .

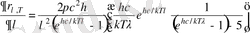Бұл туындыны нөлге теңестірп функция максимум мәніне жететін λ _мах мәнін табамыз. Онда x=hc/kTλ _мах көрінісін енгізе отырып 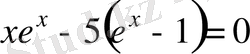теңдеуін аламыз.

Арнайы әдістермен бұл трансценденттік шешу x =4. 965 екеніне алып келеді.

hc/kTλ _мах =4, 965, бұдан Tλ _мах = hc/(4, 965К) =b,

яғни Виннің ығысу заңын аламыз.

Бір жағынан Планк формуласындағы h, k, n тұрақтыларын пайдаланып Стефан - Больцман σ және Вин b тұрақтысын анықтай аламыз. Басқа жағынан σ және b тұрақтыларының эксперименттік мәні арқылы h және k мәнін анықтауға болады.

Планк формуласы экспериментпен сәйкес келіп қана қоймай, жылулық сәулелену заңдарындағы тұрақтыларды анықтауға мүмкіндік береді. Сонымен қатар, Планк формуласы Кирхгоф қойған жылулық сәулеленудегі негізгі есептің шешімі болып табылады. Оның шешілуі тек Планктың кванттық гипотезасы көмегімен мүмкін болды.

1. 5 Оптикалық пирометрия

Жылулық сәулелену заңдары қызған және өзінен-өзі жарқырайтын денелер температурасын өлшеу үшін қолданылады. Энергетикалық жарқыраудың спектрлік тығыздығының немесе интегралдық энергетикалық жарқыраудың температураға тәуелділігін қолданып жоғары температураларды өлшеу әдістерін оптикалық пирометрия деп атайды. Қыздырылған денелердің оптикалық спектр диапазонында жылулық сәулелену интенсивтілігі бойынша температурасын өлшеуге арналған приборлар пирометрлер деп аталады. Дене температурасын өлшеу кезінде қолданылатын жылулық сәулелену заңдылықтарына байланысты дене температурасы радиациялық, түсті және ашық болып бөлінеді.

Дененің радиациялық температурасы Т _р деп қара дененің энергетикалық жарқырауының R _e (1. 5) зерттеліп отырған дененің энергетикалық жарқырауына R _T (1. 2) тең болғандағы температураны айтады. Бұл жағдайда зерттеліп отырған дененің энергетикалық жарқырауы тіркеледі және Стефан - Больцман (1. 6) заңы бойынша оның радиациялық температурасы есептеледі .

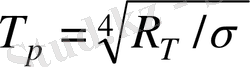Дененің радиациялық температурасы Т _р әрқашан өзінің Т температурасынан төмен болады. Бұны дәлелдеу үшін зерттеліп отырған сұр дене деп есептейік. Онда (1. 6) және (1. 4) пайдаланып мынаны жазамыз .

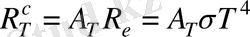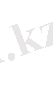
Басқа жағынан былай болады 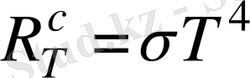. Бұларды теңестірсек .

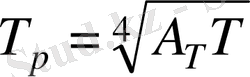Бұл жерде А _T <1 болғандықтан, T _p <T , яғни дененің өз температурасы әрқашан оның радиациялық температурасынан жоғары болады.

Дененің түсті температурасы Т _Т деп қара дененің және қарастырылып отырған дененің жарқырауының спектрлік тығыздығының салыстырмалы таралулары спектрдің көрінетін облысында өте жақын болған кездегі температурасын айтады.

Сұр денелер үшін энергетикалық жарқыраудың спектрлік тығыздығы , мұндағы А _T =const<1. Бірдей температуралы қара дене мен сұр дененің сәулелену спектрінде энергияның таралуы ұқсас болады. Сондықтан сұр денеге Виннің ығысу заңын (1. 7) қолданамыз. Зерттеліп отырған дененің энергетикалық жарқырауының максималды спектрлік тығыздығына R _{λ, T} сәйкес келетін толқын ұзындығын λ _max біле отырып оның температурасын анықтауымызға болады 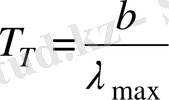. Сұр денелер үшін түсті температура дененің өз температурасымен сәйкес келеді. Сұр денеге мүлдем ұқсамайтын денелер үшін түсті температура ұғымы мағынасын жоғалтады. Осындай әдіспен жұлдыздар және Күн бетінің ( Т _Т ≈6500 К ) температуралары анықталады.

Дененің ашық температурасы Т _А деп қара дененің белгілі бір толқын ұзындығында оның энергетикалық жарқырауының спектрлік тығыздығы зерттеліп отырған дененің энергетикалық жарқырауының спектрлік тығыздығына тең болғандағы температурасын айтады, яғни (1. 12)

мұнда Т - дененің өз температурасы. Зерттеліп отырған дене үшін толқын ұзындығы λ болғанда Кирхгоф заңын (1. 3) 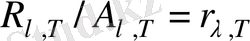және (1. 12) -ні ескеріп мынаны аламыз

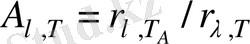(1. 13)

қара емес денелер үшін A<1 болғандықтан, , бұдан T _A <T, яғни дененің өз температурасы ашық температурадан әрқашан үлкен болады.

Ашық пирометр ретінде әдетте жойылып кететін жібі бар пирометрлер қолданылады. Пирометрдегі жіптің қыздырылуы (1. 12) шартын қанағаттандыратындай етіп алынады. Берілген жағдайда пирометр жібінің көрінісі қыздырылған дене бетінде, яғни жіп «жоғалып» кеткендей болады. Қара денеге градуирленген миллиамперметрді қолданып ашық температураны анықтауға болады.

Жарықтың жылулық көздері

Қызған денелердің жарқырауы жарық көздерін жасау үшін қолданылады. Алғашқы қыздырғыш шамдар мен доғалы шамдарды орыс ғалымдары А. Н. Лодигын және П. Н. Яблочков жаратқан.

Бір жағынан, бірдей температурада алынған кез келген толқын ұзындығы үшін қара дененің энергетикалық жарқырауының спектрлік тығыздығы қара емес денелердің энергетикалық жарқырауының спектрлік тығыздығынан үлкен болғандықтан қара денелер нағыз жарықтың жылулық көздері болуға тиіс. Алайда жылулық сәулелену селективтілігіне ие кейбір денелер (мысалы, вольфрам) үшін спектрдің көрінетін облысында сәулеленуде пайда болатын энергия бөлігі сондай температураға дейін қыздырылған қара денедегіге қарағанда әлдеқайда көп болады екен. Сондықтан вольфрам жоғары балқу температурасына ие бола отырып, шамдар жібін жасау үшін негізгі материал болады.

Вакуумдық шамдардағы вольфрамдық жіптің температурасы 2450 К -нан аспауы тиіс. Бұдан жоғары температурада жіптің тозаңданып (ыдырап) кетуі байқалады. максималды сәулелену осындай температурада ≈1, 1 мкм толқын ұзындығына сәйкес келеді, яғни адам көзінің сезімталдық максимумынан ( ≈0, 5 мкм ) өте алыс жатады. Шамды инертті газбен (мысалы, криптон және ксенонның азот қосылған қоспасы) толтырып, ≈50 кПа қысым жіп температурасын 3000 К -ге дейін көтереді. Бұл сәуленің спектрлік құрамының жақсаруына алып келеді. Бірақ жылуөткізгіштік және конвекция нәтижесінде жіп пен газ арасындағы жылу алмасудан энергия жоғалтуы әсерінен жарық шұғыласы күшеймейді. Энергия шығынын азайту үшін және жарық шұғыласы күшеюі үшін газбен толтырылған шамның жібін бір-бірін қыздырып тұратын жеке орамдар - спираль түрінде жасалады. Жоғары температура кезінде осы спираль айналасында газ қабығы пайда болады және конвекция әсерінен жылу алмасу аяқталады. Қазіргі кезде қыздырғыш шамдардың энергетикалық п. ә. к. -і 5 % -дан аспаған.

1. 7 Фотоэффект

1. 7. 1 Фотоэлектрлік эффект түрлері. Сыртқы фотоэффект заңдары

Қара дененің жылулық сәулелену есебін шешкен Планк гипотезасы кванттық теорияның қалыптасуында маңызды роль атқарған фотоэффект құбылысын түсіндіруді ары қарай дамытты. Фотоэффект сыртқы , ішкі және вентильді болып бөлінеді.

Сыртқы фотоэлектрлік эффект деп вакуумда немесе басқа ортада электромагниттік сәуле әсерінен заттың электрондар шығаруын айтамыз. Сыртқы фотоэффект қатты денелерде (металдарда, жартылай өткізгіштерде, диэлектриктерде), сұйықтарда және жеке атомды және молекулалы (фотоионизация) газдарда байқалады. Фотоэффект құбылысын 1887 ж неміс физигі Г. Герц бақылаған.

Фотоэффект құбылысына алғашқы фундаменталды зерттеу жүргізген орыс ғалымы А. Г. Столетов болды. Вакуумдық трубкада екі электрод батареяға потенциометр арқылы берілетін кернеудің мәнін ғана емес таңбасын да өзгерте алатындай етіп жалғанады. Столетов катод ретінде зерттеліп отырған металды, ал анод ретінде металдық торды пайдаланды (4 - сурет) .

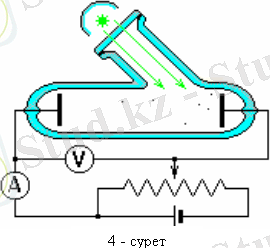
Монохроматты жарықпен катодты жарықтандырғанда пайда болатын токты тізбекке жалғанған амперметр өлшейді. Катодты толқын ұзындығы әр түрлі жарықпен жарықтандыра отырып, Столетов мынадай заңдылықтарды бекітті:

Анық эффективті әсер ультракүлгін сәуле арқылы байқалады; Жарық әсерінен зат тек теріс зарядтарын жоғалтады; Жарық әсерінен пайда болған ток күші интенсивтілікке тура пропорционал. Ағылшын физигі Дж. Дж. Томсон 1898 ж жарық әсерінен ұшып шыққан бөлшектердің жеке (меншікті) заряд шамасын өлшеді. Бұл өлшеулер жарық әсерінен электрондар шығатынын көрсетті.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.