Айналу денелері: цилиндр, конус және шардың қасиеттері, бет аудандары мен көлемдері


1
МАЗМҰНЫ
КІРІСПЕ 3
1 АЙНАЛУ ДЕНЕЛЕРІ ТУРАЛЫ ЖАЛПЫ МӘЛІМЕТТЕР 5
1. 1 Цилиндр 5
1. 2 Конус 7
1. 3 Шар және сфера 9
2 АЙНАЛУ ДЕНЕЛЕРІНІҢ БЕТІ ЖӘНЕ КӨЛЕМІ 14
2. 1 Цилиндрдің көлемі және бүйір бетінің ауданы 14
2. 2 Конустың көлемі және бүйір бетінің ауданы 15
2. 3 Шардың көлемі 17
2. 4 Шар сегменті мен секторының көлемі және сфераның ауданы 17
ҚОРЫТЫНДЫ 19
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР 22
2
КІРІСПЕ
Тақырыптың өзектілігі: Айналу денесі қозғалмайтын оське қатысты жазық фигураны айналдырғаннан пайда болған дене. Айналу денелеріне: тік
шар
Айналу денелері күнделікті тұрмыста өте көп кездесетіндігіне оқушылардың көзін жеткізеді. Цилиндрдің, конустың және шардың айналамызда қандай бейнеде екендігін, күнделікті тұрмыста цилиндрдің( су құбырлары, стакан, бөшкелер), конустың, қиық конустың(шелек, балмұздақ) және шардың ауданын, көлемін табуды үйретеді.
Айналу денелері тақырыбына есептер шығару оқушының логикалық елестету қабілетін арттырып, және сол елестету барысында пайда болған денені
түсіруді де үйретеді.
үйретуді дәлелдеуді құруға, оны аша білуге,
бағытталған ақыл -ой үрдісіне оқыту деп түсіне алу керісінше, оқушыларды дәлелдеуге үйрету мұғалім және оқулықтар ұсынған дайын дәлелдеулерге үйрету деп біледі. Дайын дәлелдеуге оқулықтарда дәлелденген немесе мұғалім көрсеткен теоремалар жатады. Кез келген дайын дәлелдеме оқушы үшін жаңалық. Сондықтан оқушылардың кітаптағы дәлелдеуді немесе мұғалімнің дәлелдеп бергенін игеруінің, оны қайта айтып бере алуының, дәлелдеу үрдісінің мәнін түсінуіне мүмкіндік беретін дидактикалық мағызы бар теоремалардың дәлелдемелерін игеру үрдісіне оқушылар енжар қатынаспай, дәлелдеуді ашушылардың бірі ретінде белсенді қатыстырылып отырылады. Теоремалардың дайын дәлелдемелерін үйрету кезінде мұғалім оқушыларды дәлелдеу әдісін іздестіре білуге, өз ойын негіздеп айта алуға, пайымдаулар жасауға дағдыландырады. Оқыту үрдісінде дәлелдеуге үйретуді дұрыс ұйымдастыру, салыстыру, анализ және синтез, жалпылау және абстракциялау тағы басқа ойлау амалдарынсыз мүмкін емес. Оқушылар теореманы берілгендері мен дәлелдеу керегін салыстыра отырып, теоремаға талдау жасайды, нәтижеде дәлелдеудің әдістері мен оны жүзеге асырудың жолдары анықталады, синездеу арқылы синтетикалық жолмен дәлелдеу үрдісі орындалады. [14] Демек, дайын дәлелдеудің оқушыларға үйрету үрдісі оқушыларды ақыл - ой қызметіне үйретуді де жүзеге асырады екен. Нәтижеде дәлелденген теоремаға ұқсас теоремаларды өз бетінше дәлелдей алу біліктіліктері мен дағдылары қалыптасады. Оқушы дәлелдеудің мән мағынасын түсініп, дәлелдеу тәсілдері мен оларға жүргізілетін ойлау амалдарын қаншалықты меңгергенімен, олардың белгілі бір тероиялық білімдер жүйесінің (ұғымдар және олардың анықтамасы, қасиеттері мен белгілері, аксиомалар мен
3
теоремалар) жеткілікті қоры жинақталмайынша дәлелдеуге үйретудің сәтсіз болары сөзсіз.
Стереометрия тарауында ең қызықты әрі терең ойлауды керек ететін "Айналу денелері" тақырыбын толық меңгеру үшін жазықтықтағы денелердің(тік төртбұрыш, тік бұрышты үшбұрыш, шеңбер, дөңгелек) қасиеттерін жақсы меңгеруі тиіс.
Жұмыстың мақсаты мен міндеттері: кеңістіктегі фигураларды, оның ішінде "Айналу денелері" тақырыбын толық талап дәрежесінде үйрету. Айналу денелерін жан-жақты зерттеп, цилиндрдің, конустың, қиық конустың, шардың және сфераның ауданын, көлемін, беттерінің аудандарын табу сияқты мәселелерді шешуге үйрету.
Оқушылардың ойлау, пікірлеу қабілеттерін арттыру, геометриялық(математикалық) білімдерін дамыту және стереометрия тарауына оның ішінде айналу денелері тақырыбына деген қызығушылығын арттыру.
Зерттеу пәні: Математиканы оқыту әдістемесі:
Зерттеу әдістері: Курстық жұмысты жазу барысында жинақтау, салыстыру, сараптау, талдау, т. б. ғылыми зерттеу әдістері пайдаланылады.
Жұмыстың құрылымы: Курстық жұмыс үш тараудан тұрады. Бірінші тарау үш пункттен, екінші тарау төрт пункттен және соңғы тарау қорытынды мен пайдаланылған әдебиеттер тізімінен тұрады. Кіріспеде жұмыстың сипаттамасы, мақсаты, міндеттері, өзектілігі қарастырылған. Курстық жұмыс-беттен тұрады.
4
1 АЙНАЛУ ДЕНЕЛЕРІ ТУРАЛЫ ЖАЛПЫ МӘЛІМЕТТЕР
1. 1 Цилиндр
Цилиндр (дәлірек айтқанда, дөңгелек цилиндр) деп бір жазықтықта жатпайтын, параллель көшіргенде дәл беттесетін екі дөңгелектен және осы дөңгелектердің сәйкес нүктелерін қосатын барлық кесінділерден қүралатын денені атайды (сурет 1) . Дөңгелектерді цилиндрдің табандары деп, ал дөңгелектер шеңберлерінің сәйкес нүктелерін қосатын кесінділерді цилиндрдің жасаушылары деп атайды. [5]
Параллель көшіру дегеніміз қозғалыс болғандықтан, цилиндрдін табандары тең болады.
Параллель көшіргенде жазықтық параллель жазықтыққа (немесе өзіне-
өзі) ауысады, ендеше, цилиндрдің табандары\ параллель жазықтықтарда жатады.
Параллель көшіргенде нүктелер параллель(немесе дәл беттесетін) түзулердің бойымен бірдей ара қашықтыққа жылжитындықтан, цилиндрдің жасаушылары параллель және тең болады.

cурет 1 cурет 2
(цилиндрлер)
Цилиндрдің беті табандарынан және бүйір бетінен құралады. Ал бүйір беті жасаушылардан түрады.
Егер цилиндрдің жасаушылары табан жазықтықтарына перпендикуляр болса, онда оны тік цилиндр деп атайды. Біз алдағы уақытта тік цилиндрді ғана қарастыратын боламыз, оны қысқаша жай ғана цилиндр дейміз. Тік цилиндрді көрнекі түрде тік төртбүрышты бір қабырғасынан осы қабырғаны ось ретінде алып, айналдырғанда жасалатын дене деп қарастыруға болады(сурет 2) . [1]
Цилиндрдің радиусы деп оның табанының радиусын атайды. Цилиндрдің
5
биіктігі деп табан жазықтықтарының ара қашықтығын атайды. Цилиндрдің осі деп табандарыньң центрлерінен өтетін түзуді атайды. Ол түзу жасаушыларға параллель болады.
Цилиндрді жазықтықтармен қию
Цилиндрді осіне параллель жазықтықпен қиғанда қимасы тік төртбұрыш болып шығады (сурет 3) . Оның екі қабырғасы - цилиндрдің жасаушылары, ал қалған екеуі табандарының параллель хордалары болады. Дербес жағдайда, осьтік цима тік төртбұрыш болып табылады. Бұл - цилиндрдің осі арқылы өтетін жазықтықпен қиғандағы қима (сурет 4)
Е с е п(1) . Цилиндрдің осьтік қимасы - квадрат, оның ауданы Q-ге тең. Цилиндрдің табанының ауданын табыңдар.
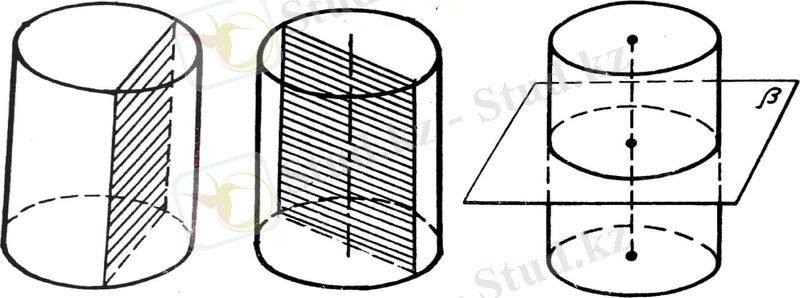
сурет 3
cурет 4
(цилиндрдің қималары)
Ш е ш у і.
Квадраттың қабырғасы
ауданы мынаған тең болады:
Т е о р е м а1. 1. Цилиндрдің табанына параллель жазықтық оның бүйір бетін табан шеңберіне тең болатын шеңбер бойымен қиып өтеді.
Д ә л е л д е у . - цилиндрдің табанына параллель жазық-тық болсын (сурет 5) . жазықтығын цилиндрдің табан жазықтығымен дәл беттестіретін цилиндр осінің бағытындағы параллель көшіру, бүйір бетін жазықтығымен қиғандағы қимасын табан шеңберімен дәл беттестіреді. Теорема дәлелденді.
Іштей және сырттай сызылған призмалар.
Цилиндрге іштей сызылған призма деп табан жазықтықтары - цилиндрдің де табан жазықтықтары, ал бүйір қырлары цилиндрдің жасаушылары болып табылатын призманы атайды (сурет 6) [11] .
6
Е с е п(2) . Цилиндрге алтыбұрышты дұрыс призма іштей сызылған. Цилиндрдің биіктігі табан радиусына тең деп алып, призманың бүйір жағының диагоналы мен цилиндр осінің арасындағы бұрышты табыңдар.
Ш е ш у і. Призманың бүйір жақтары - квадраттар, өйткені шеңберге іштей сызылған дұрыс алтыбұрыштың қабырғасы радиусқа тең (сурет 7) .

сурет 6 cурет 7
(цилиндрге іштей сызылған призмалар)
Призманың қырлары цилиндр осіне параллель, сондықтан жақтың диагоналы мен цилиндр осінің арасындағы бұрыш диагональ мен бүйір қырдың арасындағы бұрышқа тең. Бұл бұрыш 45°-қа тең, өйткені жақтары - квадраттар.
Цилиндрге жанама жазықтық деп цилиндр жасаушысы арқылы өтетін, осы жасаушыны қамтитын осьтік қимага перпендикуляр жазықтықты атайды
Цилиндрге сырттай сызылған призма табан жазықтықтары цилиндрдің табан жазықтықтары, ал бүйір жақтары цилиндрге жанасатын ризманы атайды.
1. 2 Конус
Конус (дәлірек айтсақ, дөңгелек конус) деп дөңгелектен -- конустың табанынан, бұл дөңгелектің жазықтығында жатпайтын нүктеден конустың төбесінен және конустың төбесін табанындағы шеңбердің нүктелерімен қосатын барлық кесінділерден құралған денені айтады (сурет 8) . Конустың төбесін табанындағы шеңбердің нүктелерімен қосатын кесінділер конустың жасаушылары деп аталады. Конустың беті табаны мен бүйір бетінен құралады. [8] Егер конустың төбесін табанының центрімен қосатын түзу табан жазықтығына перпендикуляр болса, ол тік конус деп аталады. Бұдан былай біз тек тік конусты ғана қарастырамыз, оны қысқаша жай ғана конус деп атаймыз. Тік дөңгелек конусты көрнекі түрде тік бұрышты үшбұрышты, оның бір катетін ось етіп алып, одан айналдырғанда пайда болатын дене деп қарастыруға болады (сурет 9) .
7

cурет 8 cурет 9
(конустар)
Конустың биіктігі деп оның төбесінен табан жазықтығына түсірілген перпендикулярды атайды. Тік конус биіктігінің табаны табанының центрімен дәл келіп беттеседі. Тік дөңгелек конустың осі деп оның биіктігін қамтитын түзуді атайды.
Конусты жазықтықпен қиғандағы қималары
Конустың төбесі арқылы өтетін жазықтықпен қиғанда қимада бүйір қабырғалары конустың жасаушылары болып табылатын, тең бүйірлі үшбұрыш шығады. Дербес жағдайда, конустың осьтік қимасы тең бүйірлі үшбұрыш болады. Осьтік қима конустың осі арқылы өтеді (сурет 10) .
Т е о р е м а. 1. 2. Конустың табан жазықтығына параллелъ жазықтық конусты дөңгелек бойымен, ал бүйір бетін центрі конустыц осінде жататын
Д ә
л
е л д е у .
конус төбесіне
қатысты
конустың
жазықтығымен
Е с е п. Конус төбесінен d қашықтықта табанына
түрлендіруі
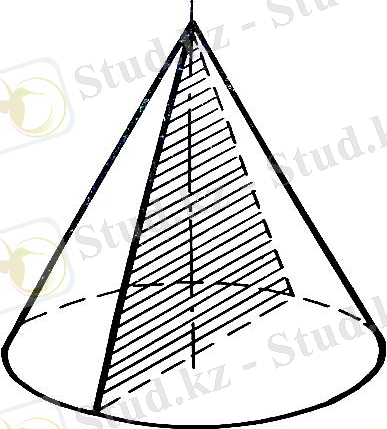
қиманың ауданы
Конустың табанына параллель және оны қиып өтетінжазықтық одан кіші конус қиып түсіреді. Қалған бөлігі қиық конус деп аталады.
8
Конусқа іштей және сырттай сызылған пирамидалар Конусқа іштей сызылған пирамида деп табаны конус табанындағы
шеңберге іштей сызылған көпбұрыш, ал төбесі конустың төбесі болып табылатын пирамиданы атайды. Конусқа іштей сызылған пирамиданың бүйір қырлары конустың жасаушылары болып табылады
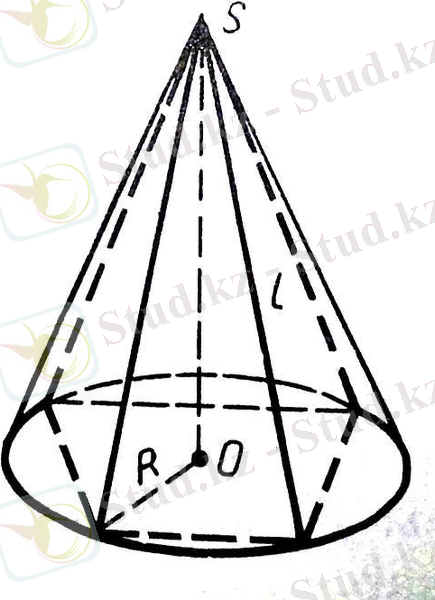
Е с е п (3) . Пирамиданың барлық бүйір қырлары тең. Оның қандай да бір конусқа іштей сызылғандығын дәлелдеңдер.
Ш е ш у і. Пирамиданың төбесінен табан жазықтығына SO перпендикулярын түсіреміз және пирамиданың бүйір қырларының үзындығын l арқылы белгілейміз (сурет 11) . Табанының төбелері О нүктесінен бірдей
қашықтықта жатады.
Бұдан шығатыны, біздің пирамидамыз төбесі
пирамиданың төбесі, ал табаны центрі О және
радиусы R дөңгелек болып табылатын сурет 11
конусқа іштей сызылған. (іштей сызылған пирамида)
Конусқа жанама жазықтық деп конус-
тың жасаушысы арқылы өтетін және осы жасаушыны қамтитын осьтік қима жазықтығына перпендикуляр жазықтықты атайды.
Конусқа сырттай сызылған пирамида деп табаны - конустың табанына сырттай сызылған көпбұрыш, ал төбесі конустың төбесімен дәл келетін пирамиданы атайды. Сырттай сызылған пирамиданың бүйір жақтарының
сурет 12
Шар бетінің екі нүктесін қосатын және шардың
(шар)
сурет 13
(шардың диаметрлік жазықтығы)
келген диаметрдің ұштары шардың диаметрлік қарама-қарсы нүктелері деп аталады. Шар да цилиндр мен конус сияқты, айналу денесі болып табылады. Ол жарты дөңгелекті диа-метрінен айналдырғанда шығады(сурет 12) .
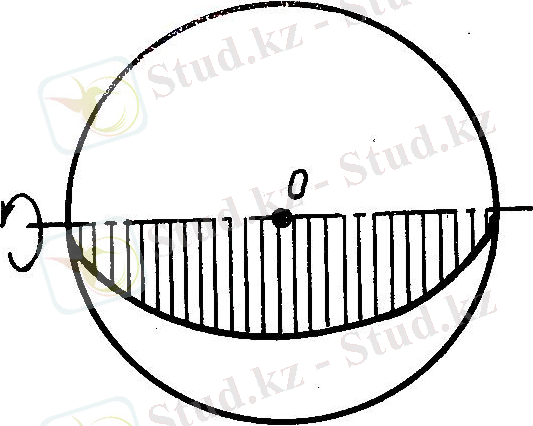
Шарды жазықтықпен қию Т е о р е м а 1 . 3 . Шарды жазықтықпен қиғандағы кез келген қимасы
дөңгелек болады. Бұл дөңгелектің центрі шардың центрінен қиюшы жазықтыққа түсірілген перпендикулярдың табаны болып табылады.
жазықтығына
О'
нүктесінен
олай
болса, ол
центрі
О' және радиусы
дөңгелекке тиісті.
Керісінше: бұл дөңгелектің кез келген нүктесі шарға тиісті болады. Ал бүл - шардың жазықтығымен қимасы центрі О' нүктесінде болатын дөңгелек деген сөз. Теорема дәлелденді.
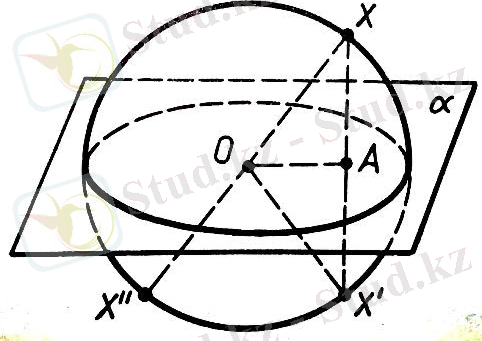
Шардың центрінен өтетін жазықтық диаметрлік жазықтық деп аталады. Шардың диаметрлік жазықтықпен қиғандағы қимасы - үлкен дөңгелек (-сурет) деп, ал сфераның қимасы үлкен шеңбер деп аталады.
Е с е п(3) . Шар радиусының ортасынан оған перпендикуляр жазықтық жүргізілген. Шыққан қим ауданының дөңгелек ауданына қатынасы қандай болады?
Ш е ш у і. Егер шар радиусы R болса, онда қимадағы дөңгелек радиусы
.
Бұл дөңгелектің ауданының үлкен дөңгелектің ауданының қатынасына қатынасы
Шардың симметриясы Т е о р е м а1. 4. Шардың кез келген
диаметрлік жазытығы оның симметрия жазықтығы болып табылады. Шардың центрі
оның симметрия центрі болып табылады
10
Д ә л е л д е у. α - шардың диаметрлік жазықтығы және Х- еркімізше алынған нүктесі болсын (сурет 13) . α жазықтығына қарағанда X нүктесіне симметриялы X' нүктесін саламыз.
α жазықтығы XX' кесіндісіне перпендикуляр және ол кесіндіні ортасында (А нүктесінде) қияды. Тік бұрышты ОАХ және ОАХ' үшбұрыштарының теңдігінен ОХ' = ОХ болып шығады .
болғандықтан, , яғни X нүктесіне симметриялы нүкте шарға тиісті болады. Теореманың бірінші түжырымы дәлелденді.
Енді X" - шардың центріне қарағанда X нүктесіне симметриялы нүкте болсын. Сонда ОХ" = , яғни X" нүктесі шарға тиісті. Теорема толық дәлелденді.
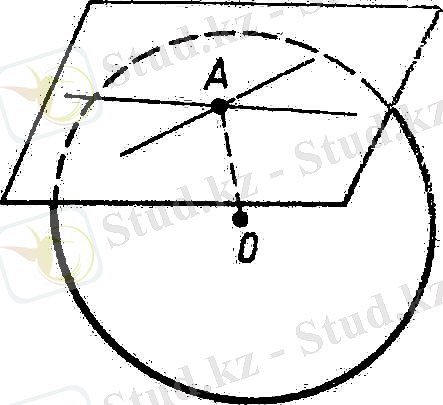
Шарға жанама жазықтық
Шар бетінің А нүктесінен өтетін және А нүктесіне жүргізілген радиусқа перпендикуляр жазықтық жанама жазықтық деп аталады. А нуктесі жанасу нүктесі деп аталады(сурет 14)
сурет 14
(шарға жанама жазықтық)
- е о р е м а1. 5. Жанама жазықтықтың шармен бір ғана ортақ нүктесі
- жанасу нүктесі болады.
Д ә л е л д е у. α - шарға жанама жазықтық және А - жанасу нүктесі болсын α жазықтыгынан А -дан өзге X нүктесін еркімізше аламыз. ОА - перпендикуляр, ал ОХ - көлбеу болгандықтан,
Олай болса, X нүктесі шарға тиісті емес. Теорема дәлелденді.
Шарға жанама жазықтықта жататын және жанасу нүктесі арқылы өтетін түзу осы нүктеде
ғанаортақ
(шарға жанама үшбұрыш)
11
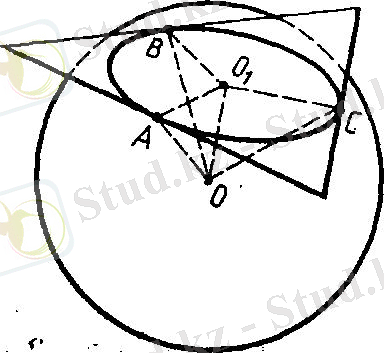
Е с е п (4) . Радиусы R шар қабырғасы а болатын дұрыс үшбұрыштың барлық қабырғаларын жанайды. Шар центрінен үшбұрыш жазықтығына дейінгі қашықтықты табыңдар.
Ш е ш у і. А, В, С- шардың үшбұрыш қабыр-ғаларымен жанасу нүктелері болсын (сурет 15) .
Шардың О центрінен үшбұрыш жазықтығына ОО 1 перпендикулярын түсіреміз.
ОА, ОВ және ОС кесінділері қабырғаларға түсірілген перпендикулярлар. Үш перпендикуляр туралы теорема бойынша О 1 А, О 1 В және О 1 С кесінділері де үш-бүрыштың сәйкес қабырғаларына перпендикуляр болады
... жалғасыТік бұрышты ОО 1 А, ОО 1 В, ОО 1 С үшбұрыштарының теңдігінен (ОО 1
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz