Туынды ұғымы және оның есептеу теоремалары мен қолданбалары


мазмұны
кІРІСПЕ . . . 3
1 ТУЫНДЫ ҰҒЫМЫН ТУҒЫЗАТЫН МЫСАЛДАР . . . 5
1. 1 Жанама туралы есеп . . . ………. . 5
1. 2 Материялық нүктенің лездік жылдамдығы. . …… . . . 7
2 БІР АЙНЫМАЛДЫ ФУНКЦИЯНЫҢ ТУЫНДЫСЫ ТУРАЛЫ ҰҒЫМ. . 8
2. 1 Туындының анықтамасы, біржақты туындылар, шексіз туындылар…… . . . 8
2. 2 Туындының геометриялық және физикалық мағыналары . . . 12
2. 3 Күрделі функцияның туындысы, кері функцияның туындысы . . . 13
3 ТУЫНДЫНЫ ЕСЕПТЕУДІҢ НЕГІЗГІ ТЕОРЕМАЛАРЫ ЖӘНЕ ҚОЛДАНУЛАРЫ . . . 16
3. 1 Орта мән жайындағы теоремалар . . . …16
ҚОРЫТЫНДЫ . . . … . . . ………. ……. 22
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . . …… . . . …… . . . 24
КІРІСПЕ
Тақырыптың өзектілігі.
Туындылар және олардың функцияларды зерттеуде қолданылуы қарастырылатын математиканың бөлімі дифференциалдық есептеу деп аталады. «Туынды» термині derivee деген француз сөзінің қазақша сөзбе - сөз аудармасы, оны 1797ж. Ж. Лагранж (1736 - 1813) енгізілген, қазіргі кездегі
 белгілеулерін енгізген еді.
белгілеулерін енгізген еді.
Математиканың негізгі міндеттерінің бірі функцияларды зерттеу. Функцияның өсетін және кемитін аралықтарын, эктремум мәндерін, нөлдерін, ең үлкен және ең кіші мәндерін табу және басқа да қасиеттерін туынды көмегімен табуға болады. Туындыны қолданғанда функцияны зерттеу, сонымен бірге оның графигін салу біршама оңай болады.
Туынды - функция өзгеруінің лездік жылдамдығы, сондықтан да туынды физикада кең түрде қолданылады. Мысалы: егер материалдық нүкте түзу сызықты қозғалып, оның координаты
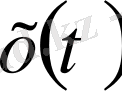 заңы бойынша өзгеретін болса, онда
заңы бойынша өзгеретін болса, онда
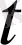 уақыт мезетіндегі оның
уақыт мезетіндегі оның
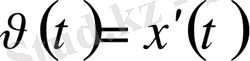 жылдамдығы туындығы тең болады.
жылдамдығы туындығы тең болады.
Сонымен бірге кейбір химиялық есептерді шығарғанда туынды кең түрде қолданылады. Мысалы: егер
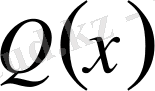 - химиялық реакцияға қатысқан зат мөлшерінің өзгеру заңы болса, онда химиялық рекцияның
- химиялық реакцияға қатысқан зат мөлшерінің өзгеру заңы болса, онда химиялық рекцияның
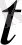 уақыт мезетіндегі
уақыт мезетіндегі
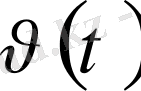 жылдадығы туындығы тең болады:
жылдадығы туындығы тең болады:
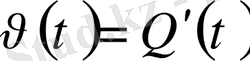 .
.
Математикалық физика даму процесінде жазбалық ғылымнан нақты ғылымға біртіндеп айнала бастады. Табиғатта және техникада өтетін әртүрлі құбылыстар және процестерді зерттегенде физиктер математикалық әдістерді кеңірек қолданады[1] .
Курстық жұмыстың мақсаты мен міндеттері. Туындының көмегімен функцияны зерттеп графигін салу, теңсіздіктерді дәлелдеу, функцияның графигіне х 0 жүргізілген жанаманың теңдеуін құру, функцияның ең үлкен және ең кіші мәндерін, табудың тиімді әдістерін қарастыру және оларды қолданып есептер шығаруды үйрену.
Зерттеу пәні. Математика оқыту әдістемесі
Зерттеу әдістері. Курстық жұмысты жазу барысында жинақтау, салыстыру, жүйелеу, сараптау, талдау т. б. ғылыми зерттеу әдістері пайдаланылады.
Курстық жұмыстың құрылымы.
Курстық жұмыс 3 тарау, 6 тараушалардан тұрады. 1-ші тарауда туынды ұғымын туғызатын мысалдар және кейбір қажетті түсініктер мен ұғымдар берілген.
2-ші тарау 3 тараушадан тұрады. 1-ші, 2-ші тараушаларда туындының анықтамасы, бір жақты туындылар, туындының геометриялық және физикалық мағынасы туралы қысқаша мәлімет беріледі.
3-ші тараушада күрделі функцияның туындысы, кері функцияның туындысы келтіріліп шығарылады. Бұған бірнеше мысалдар келтіріледі.
Сонымен бірге жұмыста функцияны толық зерттеп, графигін салудың бірнеше дербес жағдайлары да қарастырылған.
Курстық жұмыстың құрылымы 24 беттен тұрады
1 ТУЫНДЫ ҰҒЫМЫН ТУҒЫЗАТЫН МЫСАЛДАР
1. 1 Жанама туралы есеп
Біздер шеңбердің жанамасы ұғымымен таныспыз. Шеңберге жүргізілген жанаманың сол шеңбермен жалғыз ортақ нүктесі бар, сондай-ақ шеңбер түзудің бір жағында орналасқан болатын. Енді жазықтықта кез келген қисық берілген болса, оған жүргізілген жанаманы қандай анықтау мүмкін деген мәселеге қаралық.
Жанаманы қисықпен жалғыз ортақ нүктесі бар болған түзу деп анықтауға болмайды, себебі, мысалы, y=ax 2 парабола және оның симметрия осі тек бір ортақ нүктесі бар, бірақ параболаның симметрия осі жанама болмайды. Қисық жанама түзудің бір жағында орналасуы да маңызды емес, себебі y=ax 3 қисыққа абссцисса осі (0; 0) нүктеде жанасады, бірақ қисық бұл осьті сол нүктеде қиып өтеді. Жанаманың қисықпен жалғыз ортақ нүктесі бар болуы да оның маңызды қасиеті бола алмайды. Мысалы: x=1 түзу y=sinx синусоидамен шексіз көп ортақ нүктелері бар, бірақ ол синусоида жанамасы болады (сурет 1) .

Сурет 1 Синус функцияның графигіне жүргізілген жанамасы
Жанамаға анықтама беру үшін шек ұғымынан пайдалануға тура келеді. Айталық, Г қандай да бір қисық доғасы, M 0 сол қисықтың нүктесі болсын. Қисыққа тиісті N нүктені таңдап, M 0 N түзуді өткіземіз. Бұл түзу осы қисыққа жүргізілген қиюшы деп аталады (сурет 2) . Егер N нүкте қисық бойымен M 0 нүктеге ұмтылса, M 0 N түзу M 0 нүкте маңында бұрылады. N нүкте M 0 нүктеге жақындаған сайын M 0 N қиюшы қандай да бір M 0 T шектік түзуге ұмтылуы мүмкін. Бұл жағдайда M 0 T түзу Г қисықтың M 0 нүктесіндегі жанамасы делінеді. Қисықтың жанамасы 3-ші және 4-ші суреттердегідей жағдайда болуы да мүмкін (сурет 2) .
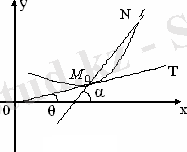
Сурет 2 Қисыққа жүргізілген жанама графигі
Егер қиюшының шектік түзуі бар болмаса, онда M 0 нүктеде жанама жүргізу мүмкін емес делінеді. Мұндай жағдай M 0 нүкте қисықтың сыну нүктесі болғанда орынды болады (сурет 3 а, в, с) .
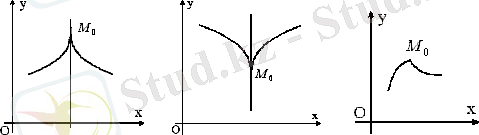
а) ә) б)
Сурет 3
Қисыққа жүргізілген жанама графигінің 3-түрлі жағдайы.
Қисық жанамасының бұрыштық коэффициентін табу жөніндегі есеп. Енді Г қисық қандай да бір аралықта анықталған үзіліссіз y=f(x) функцияның графигі болған жағдайда жанаманың бұрыштық коэффициентін табайық. f(x) функцияның графигі болған Г сызыққа тиісті M 0 нүктенің абсциссасы x 0 , координатасы f(x 0 ) және сол нүктеде жанама бар деп қарастырайық.
Г сызықта M 0 нүктеден өзгеше N(x 0 +∆x, f(x 0 +∆x) ) нүктені алып, М 0 N қиюшы өткіземіз. Оның Ox осінің оң бағытымен жасаған бұрышын α әрпімен белгілейміз (сурет 4) .
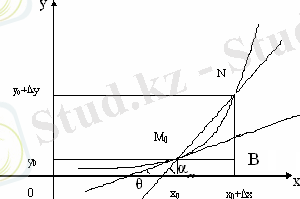
Сурет 4 Қисықтың Ox осінің оң бағытымен α бұрыш жасауының графигі
Шынында, α бұрыш ∆x -ке тәуелді болады: α=α(∆x) және tgα=
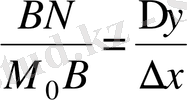 орынды[2] .
орынды[2] .
Жанаманың абсцисса осінің оң бағытымен жасаған бұрышын θ әрпімен белгілейміз. Егер θ≠π/2 болса, онда tgα функцияның үзіліссіздігі бойынша k
жанама
=tgθ =
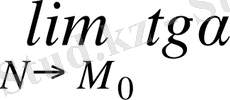 , және N нүктенің M
0
нүктеге ұмтылуы ∆x-тің 0-ге ұмтылуына тең екендігін еске алсақ, k
жанама
=
, және N нүктенің M
0
нүктеге ұмтылуы ∆x-тің 0-ге ұмтылуына тең екендігін еске алсақ, k
жанама
=
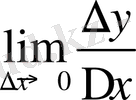 теңдікті аламыз.
теңдікті аламыз.
Сонымен, y=f(x) функцияның абсциссасы x
0
болған нүктесінде вертикаль болмаған жанама өткізу мүмкін болуы үшін сол нүктеде
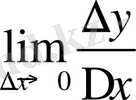 шектің бар болуы қажетті және жеткілікті, сондай-ақ, шек жанаманың бұрыштық коэффициентіне тең болады екен.
шектің бар болуы қажетті және жеткілікті, сондай-ақ, шек жанаманың бұрыштық коэффициентіне тең болады екен.
1. 2 Материялық нүктенің лездік жылдамдығы
Айталық материалдық нүкте s=s(t) заңмен түзу сызықты қозғалыста болсын. Физикада нүктенің t
0
және t
0
+∆t уақыт аралығында басып өткен ∆s=s(t
0
+∆t) -s(t
0
) жолдың сол уақыт аралығына қатынасы нүктенің орташа жылдамдығы деп аталады: v
орташа
=
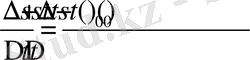 . Шынында, ∆t қаншалық кіші болса,
. Шынында, ∆t қаншалық кіші болса,
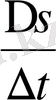 орташа жылдамдық нүктенің t
0
уақыттағы жылдамдығына соншалықты жақын болады. Сол себепті нүктенің t
0
уақыттағы лездік жылдамдығы деп [t
0
; t
0
+∆t] уақыт аралығындағы орташа жылдамдықтың ∆t нөлге ұмтылғандағы шегіне айтылады.
орташа жылдамдық нүктенің t
0
уақыттағы жылдамдығына соншалықты жақын болады. Сол себепті нүктенің t
0
уақыттағы лездік жылдамдығы деп [t
0
; t
0
+∆t] уақыт аралығындағы орташа жылдамдықтың ∆t нөлге ұмтылғандағы шегіне айтылады.
Сонымен,
v
лездік
=
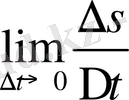 .
.
Жоғарыдағы екі түрлі есепті шешу бір нәтижеге - функция өсімшесінің аргумент өсімшесіне болған қатынасының аргумент өсімшесі нөлге ұмтылғандағы шегін есептеуга келтірілді.
Мәліметтерге қарағанда, табиғат, қоғам және техникалардағы көптеген мәселелер жоғарыдағыға ұқсас шектерді есептеуді талап етеді екен. Сол себепті оны жеке зерттеу пайдалы болады.
2 БІР АЙНЫМАЛДЫ ФУНКЦИЯНЫҢ ТУЫНДЫСЫ ТУРАЛЫ ҰҒЫМ
2. 1 Туындының анықтамасы, біржақты туындылар, шексіз туындылар
Айталық f(x) функция (a, b) интервалында анықталған болсын. Бұл интервалға тиісті x 0 нүкте алып, оған x 0 +∆x∈(a, b) болатындай ∆x өсімше берейік. Нәтижеде f(x) функция да x 0 нүктеде ∆y=f(x 0 +∆x) -f(x 0 ) өсімше алады.
Анықтама. Егер ∆x нөлге ұмтылғанда
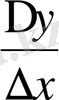 қатынастың шегі
қатынастың шегі
 бар және шекті болса, бұл шек f(x) функцияның x
0
нүктедегі туындысы делінеді және f’(x
0
), немесе y’(x
0
), немесе
бар және шекті болса, бұл шек f(x) функцияның x
0
нүктедегі туындысы делінеді және f’(x
0
), немесе y’(x
0
), немесе
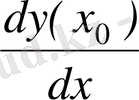 , кейде
, кейде
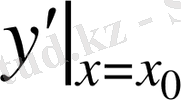 немесе
немесе
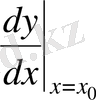 арқылы белгіленеді.
арқылы белгіленеді.
Демек,
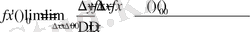 .
.
Мұнда x 0 +∆x=x деп алайық. Онда ∆x=x-x 0 және ∆x нөлге ұмтылғанда x айнымалы x 0 -ге ұмтылады, нәтижеде

болады. Демек, f(x) функцияның x
0
нүктедегі туындысы x айнымалының x
0
-ге ұмтылғандағы
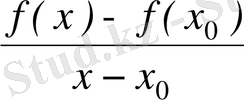 қатынастың шегі деп те анықталуы мүмкін:
қатынастың шегі деп те анықталуы мүмкін:
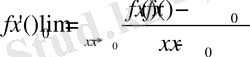 .
.
x 0 нүктеде туындысы бар болған функция сол нүктеде дифференциалданатын функция делінеді. Егер f(x) функция (a, b) интервалдың әрбір нүктесінде дифференциалданатын болса, ол (a, b) интервалында дифференциалданатын функция делінеді[3] .
Туынды табу амалы дифференциалдау амалы деп аталады.
Жоғарыдағы шек бар болған әрбір x 0 нүктеге анық бір сан сәйкес келеді, демек f’(x) - бұл жаңа функция болып, ол жоғарыдағы шек бар болған барлық x нүктелерде анықталған. Бұл функция f(x) функцияның туынды функциясы, әдетте, туындысы деп аталады.
Енді туынды анықтамасынан пайдаланып, y=f(x) функция туындысын табудың төмендегі алгоритмін беруге болады:
1) бекітілген x аргументтің мәніне сәйкес функцияның f(x) мәнін табу;
2) x аргументке f(x) функцияның анықталу облысынан шығып кетпейтіндей ∆x өсімше беріп, f(x+∆x) -ті табу;
3) функцияның ∆f(x) =f(x+∆x) -f(x) өсімшесін есептеу;
4)
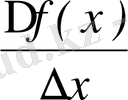 қатынасты құрастыру;
қатынасты құрастыру;
5)
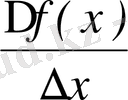 қатынастың ∆x нөлге ұмтылғанда шегін есептеу.
қатынастың ∆x нөлге ұмтылғанда шегін есептеу.
1-мысал. f(x) =kx+b функцияның туындысын тап.
Шешу. Туынды табу алгоритмінен пайдаланамыз.
1) х аргументті бекітіп, функцияның мәнін есептейміз:
f(x) =kx+b;
2) аргументке ∆х өсімше береміз, онда
f(x+∆x) =k(x+∆x) +b=kx+k∆x+b.
3) функцияның өсімшесі ∆f(x) =f(x+∆x) -f(x) =(kx+k∆x+b) -
( kx+b) =k∆x.
4)
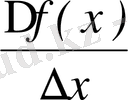 =
=
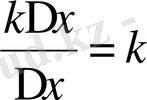 ;
;
5)
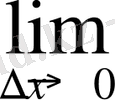
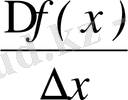 =
=
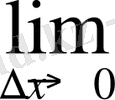 k=k.
k=k.
Демек, (kx+b) ’=k екен.
Дербес жағдайда, f(x) =b тұрақты функция (бұл жағдайда k=0) үшін (b) ’=0; f(x) =x (k=1) функция үшін x’=1 болады.
2-мысал. f(x) =x 2 функцияның туындысын тап.
Шешу. Жоғарыдағы алгоритмнен пайдаланамыз.
1) х аргументті бекітіп, функция мәнін есептейміз: f(x) = x 2 ;
2) аргументке ∆х өсімше береміз, онда
f(x+∆x) =(x+∆x) 2 =x 2 +2x∆x+(∆x) 2 ;
3) функцияның өсімшесі ∆f(x) =f(x+∆x) -f(x) =(x 2 +2x∆x+(∆x) 2 ) -x 2 = =∆x(2x+∆x) ;
4)
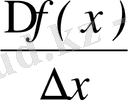 =
=
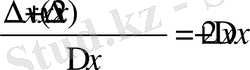 ;
;
5)
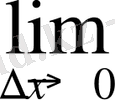
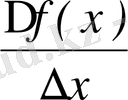 =
=
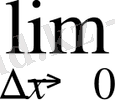 (2x+∆x) =2x.
(2x+∆x) =2x.
Демек, (x 2 ) ’=2x екен.
3-мысал. f(x) =
 функцияның туындысын тап.
функцияның туындысын тап.
Шешу. 1) f(x) =
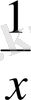 ;
;
2) f(x+∆x) =
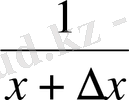 . Бұл жерде жалпы алғанда x>0 және ∆x<x деп есептейміз;
. Бұл жерде жалпы алғанда x>0 және ∆x<x деп есептейміз;
3) ∆f(x) =f(x+∆x) -f(x) =
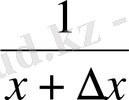 -
-
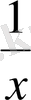 =
=
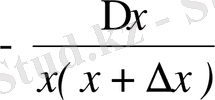 ;
;
4)
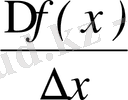
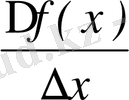 =
=
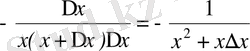 ;
;
5)
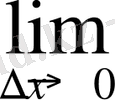
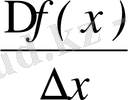 =
=
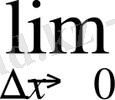 (
(
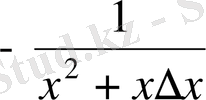 ) =
) =
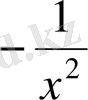 .
.
Демек,
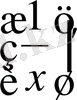 =
=
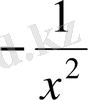 .
.
Туындысы бар болған функцияның үзіліссіздігі. f(x) функцияның x 0 нүктеде туындысы бар болуы мен оның сол нүктеде үзіліссіз болуы арасында төмендегідей байланыс бар:
Теорема. Егер f(x) функцияның x 0 нүктеде туындысы бар болса, онда функция сол нүктеде үзіліссіз болады.
Дәлелдеу. 1-тәсіл. Айталық, f(x) функцияның x
0
нүктеде туындысы бар болсын:
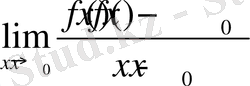 =
=
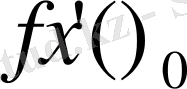 . Барлық x≠x
0
нүктелерде мына теңдік орынды:
. Барлық x≠x
0
нүктелерде мына теңдік орынды:
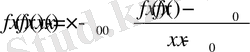 . Онда көбейтіндінің шегі жайындағы теорема бойынша
. Онда көбейтіндінің шегі жайындағы теорема бойынша
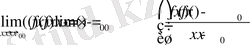

болады. Бұл f(x) функцияның x 0 нүктеде үзіліссіздігін білдіреді.
2-тәсіл. Функцияның x
0
нүктедегі туындысын анықтама бойынша былай жазуға болады:
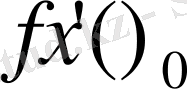
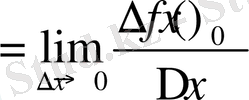 . Бұл теңдіктің оң жағындағы шекті
. Бұл теңдіктің оң жағындағы шекті
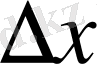 айнымалының
айнымалының
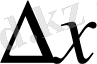 нөлге ұмтылғандағы шегі деп қарастырсақ, онда
нөлге ұмтылғандағы шегі деп қарастырсақ, онда
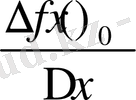
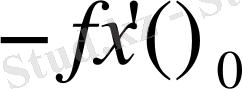 айырым
айырым
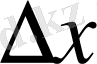 нөлге ұмтылғанда шексіз аз шама болады, оны
нөлге ұмтылғанда шексіз аз шама болады, оны
 арқылы белгілейміз. Сонымен
арқылы белгілейміз. Сонымен
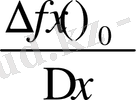
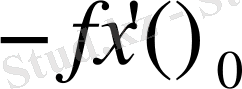
 болып, төмендегі теңдік орынды болады:
болып, төмендегі теңдік орынды болады:
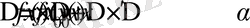 , бұл жерде
, бұл жерде
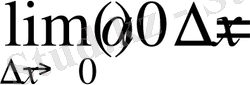 .
.
Бұл формула функция өсімшесінің формуласы деп аталады. Бұл формуладан
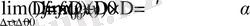 екендігі келіп шығады. Демек f(x) функцияның x
0
нүктеде үзіліссіз. Теорема дәлелденді.
екендігі келіп шығады. Демек f(x) функцияның x
0
нүктеде үзіліссіз. Теорема дәлелденді.
Бұл теореманың керісі орынды емес, яғни функцияның нүктеде үзіліссіздігінен оның сол нүктеде туындысы бар болуы келіп шыға бермейді. Мысалы, y=x функция x-тің барлық мәндерінде, сондай-ақ, x=0 нүктеде үзіліссіз. Бұл функцияның х=0 нүктедегі өсімшесі ∆y=∆x болып, бұдан
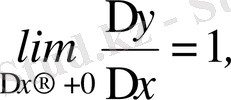
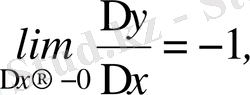
және
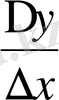 қатынастың ∆x→0-де шегі жоқ екендігі келіп шығады, демек f(x) =x функцияның x=0 нүктеде туындысы жоқ.
қатынастың ∆x→0-де шегі жоқ екендігі келіп шығады, демек f(x) =x функцияның x=0 нүктеде туындысы жоқ.
Бір жақты туындылар Анықтама. Егер ∆x нөлге оңнан (солдан) ұмтылғанда
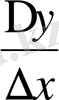 қатынастың шегі
қатынастың шегі
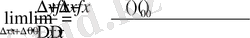
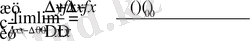 бар және шекті болса, бұл шек f(x) функцияның x
0
нүктедегі оң (сол) туындысы деп аталады және
бар және шекті болса, бұл шек f(x) функцияның x
0
нүктедегі оң (сол) туындысы деп аталады және
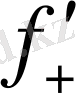 (x
0
) (
(x
0
) (
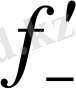 (x
0
) ) арқылы белгіленеді.
(x
0
) ) арқылы белгіленеді.
Әдетте функцияның оң және сол туындылары бір жақты туындылар деп аталады.
Жоғарыдағы мысалдан, f(x) =x функцияның x=0 нүктедегі оң туындысы «1»-ге, сол туындысы «- 1»-ге теңдігі келіп шығады[4] .
Функция туындысының анықтамасы мен бір жақты туынды анықтамаларынан және функция шегі бар болуының қажетті және жеткілікті шартынан төмендегі теореманың орынды екендігі келіп шығады:
Теорема. Айталық f(x) функция x
0
нүктенің қандай да бір маңында үзіліссіз болсын. Онда f(x) функция x
0
нүктеде f’(x
0
) туындысы бар болуы үшін
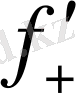 (x
0
),
(x
0
),
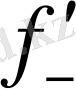 (x
0
) бір жақты туындылар бар, сонымен қатар
(x
0
) бір жақты туындылар бар, сонымен қатар
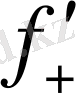 (x
0
) =
(x
0
) =
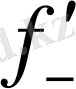 (x
0
) теңдіктің орынды болуы қажетті және жеткілікті болады.
(x
0
) теңдіктің орынды болуы қажетті және жеткілікті болады.
Бұл теореманы дәлелдеуді оқырманға жаттығу есебінде қалдырамыз.
Шексіз туындылар. Кейбір нүктелерде
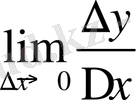 шек +∞ (-∞) -ге тең болуы мүмкін. Бұндай жағдайларда сол нүктелерде функция шексіз туындысы бар немесе функцияның туындысы шексізге тең делінеді.
шек +∞ (-∞) -ге тең болуы мүмкін. Бұндай жағдайларда сол нүктелерде функция шексіз туындысы бар немесе функцияның туындысы шексізге тең делінеді.
Мына
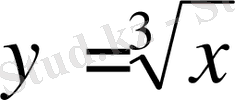 функция үшін ∆y/∆x қатынастың ∆x нөлге ұмтылғандағы шегін қарайық. Функцияның 0 нүктеде өсімшесін есептейміз: ∆y=∆f(0) =f(0+∆x) -f(0) =f(0+∆x) =f(∆x) =
функция үшін ∆y/∆x қатынастың ∆x нөлге ұмтылғандағы шегін қарайық. Функцияның 0 нүктеде өсімшесін есептейміз: ∆y=∆f(0) =f(0+∆x) -f(0) =f(0+∆x) =f(∆x) =
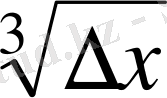 .
.
Функция өсімшесінің аргумент өсімшесіне қатынасы
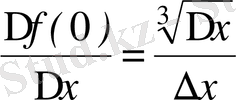 =
=
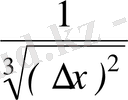 және бұл қатынастың ∆x нөлге ұмтылғандағы шегі +∞ -ге тең.
және бұл қатынастың ∆x нөлге ұмтылғандағы шегі +∞ -ге тең.
Демек,
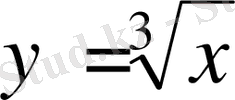 функцияның x=0 нүктеде шексіз туындысы бар екен.
функцияның x=0 нүктеде шексіз туындысы бар екен.
Шексіз туынды үшін де бір жақты шексіз туынды ұғымын қарауға болады.
Егер y=f(x) функция x=x 0 нүктеде +∞ (-∞) туындысы бар болса, онда
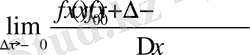 =
=
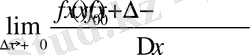 =+∞ (-∞)
=+∞ (-∞)
қатынастың орынды екендігін дәлелдеу мүмкін. Бұл тұжырымның керісі де орынды екендігі айқын.
Берілген x
0
нүктеде
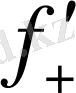 (x
0
) =+∞,
(x
0
) =+∞,
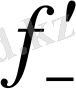 (x
0
) =-∞,
(x
0
) =-∞,
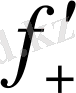 (x
0
) =-∞,
(x
0
) =-∞,
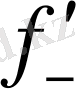 (x
0
) =+∞) болуы да мүмкін. Мұндай жағдайда f(x) функция x=x
0
нүктеде туындысы (шексіз туындысы да) жоқ деп есептеледі.
(x
0
) =+∞) болуы да мүмкін. Мұндай жағдайда f(x) функция x=x
0
нүктеде туындысы (шексіз туындысы да) жоқ деп есептеледі.
Мысал ретінде y=
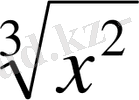 функцияның x=0 нүктедегі бір жақты туындыларды анықтайық. Бұл функцияның x=0 нүктедегі өсімшесі ∆y(0) =
функцияның x=0 нүктедегі бір жақты туындыларды анықтайық. Бұл функцияның x=0 нүктедегі өсімшесі ∆y(0) =
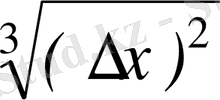 және
және
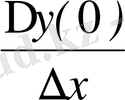 =
=
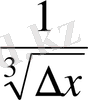 екендігін көру қиын емес. Сол себепті
екендігін көру қиын емес. Сол себепті
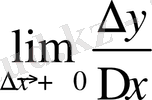 =+∞ және
=+∞ және
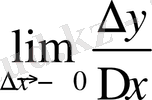 =-∞ болады. Демек, y’
-
(0) =-∞, y’
+
(0) =+∞ болып, функция x=0 нүктеде шексіз туындысы жоқ[5] .
=-∞ болады. Демек, y’
-
(0) =-∞, y’
+
(0) =+∞ болып, функция x=0 нүктеде шексіз туындысы жоқ[5] .
2. 2 Туындының геометриялық және физикалық мағыналары
Туындының геометриялық мағынасы. Жоғарыда біз, егер y=f(x) функция графигінің M
0
(x
0
; f(x
0
) ) нүктесінде жанамасы бар болса, онда жанаманың бұрыштық коэффициенті k
жанама
=
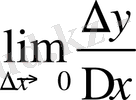 екендігін көрсеткен едік. Бұдан туындының геометриялық мағынасы келіп шығады:
екендігін көрсеткен едік. Бұдан туындының геометриялық мағынасы келіп шығады:
y=f(x) функция графигіне абсциссасы x=x 0 болған нүктесіндегі жанаманың бұрыштық коэффициенті туындының сол нүктедегі мәніне тең: k жанама =f’(x 0 ) .
Айталық y=f(x) функция x=x 0 нүктеде үзіліссіз және f’(x 0 ) =+∞ болсын. Онда функция графигінің абсциссасы x=x 0 нүктесінде вертикал жанамасы бар болады, оған қатысты функцияның графигі көрсетілгендей орналасады.
Дәл сол сияқты f’(x 0 ) =-∞ болғанда да x=x 0 нүктеде функция графигінің вертикал жанамасы бар болады, функцияның графигі жанамаға қатысты көрсетілгендей орналасады (сурет 8) .
Егер
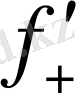 (x
0
) =+∞ және
(x
0
) =+∞ және
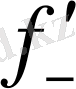 (x
0
) =-∞ болса, онда функция графигінің x=x
0
нүкте маңында болады. Дәл сол сияқты,
(x
0
) =-∞ болса, онда функция графигінің x=x
0
нүкте маңында болады. Дәл сол сияқты,
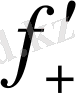 (x
0
) =-∞ және
(x
0
) =-∞ және
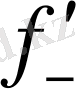 (x
0
) =+∞ болғанда, функцияның графигі x=x
0
нүкте маңында 3-суреттегідей түрде болады. Мұндай жағдайларда (x
0
, f(x
0
) ) нүктеде жанама бар, бірақ туынды жоқ. Егер x=x
0
нүктеде шекті бір жақты туындылар бар, бірақ
(x
0
) =+∞ болғанда, функцияның графигі x=x
0
нүкте маңында 3-суреттегідей түрде болады. Мұндай жағдайларда (x
0
, f(x
0
) ) нүктеде жанама бар, бірақ туынды жоқ. Егер x=x
0
нүктеде шекті бір жақты туындылар бар, бірақ
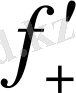 (x
0
) ≠
(x
0
) ≠
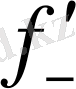 (x
0
) болса, онда функцияның графигі сурет 5 ұқсас түрде болады. (x
0
, f(x
0
) ) нүкте графиктің сыну нүктесі болады[6] .
(x
0
) болса, онда функцияның графигі сурет 5 ұқсас түрде болады. (x
0
, f(x
0
) ) нүкте графиктің сыну нүктесі болады[6] .
Туындының физикалық мағынасы. Туынды ұғымына алып келетін екінші мәселеде қозғалыс заңы s=s(t) функциямен анықталған түзу бойынша қозғалыстағы материалық нүктенің t уақыттағы лездік жылдамдығы v
лездік
=
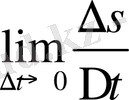 екендігін көрген едік. Бұдан туындының физикалық (механикалық) мағынасы келіп шығады(сурет 5, а, ә) .
екендігін көрген едік. Бұдан туындының физикалық (механикалық) мағынасы келіп шығады(сурет 5, а, ә) .
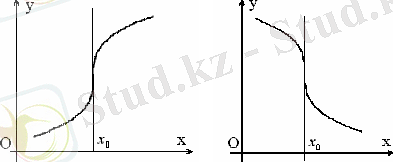
а) ә)
Сурет 5
Қисыққа жүргізілген вертикал жанамалардың графиктері
s=s(t) функциямен анықталған түзу бойынша қозғалыстың t уақыт моментіндегі қозғалыс жылдамдығының сан мәні туындыға тең: v лездік =s’(t) .
Туындының механикалық мағынасын қысқаша төмендегідей айту мүмкін: жолдан уақыт бойынша алынған туынды жылдамдыққа тең.
Туынды ұғымы тек түзу бойынша қозғалыстың лездік жылдамдығын, тағы басқа да процестердің лездік жылдамдығын анықтауға көмек береді. Мысалы, айталық y=Q(T) денені T температураға дейін қыздыру үшін берілетін жылулық мөлшерінің өзгеруін бейнелейтін функция болсын. Онда дененің жылу сыйымдылығы жылулық мөлшерінен температура бойынша алынған туындысына тең болады:
C=
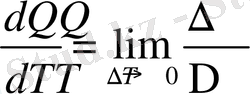 .
.
Жалпы алғанда, туындыны f(x) функциямен өрнектелетін процестің лездік жылдамдығы математикалық моделі деп айтуға болады[7] .
2. 3 Күрделі функцияның туындысы, кері функцияның туындысы
Айталық, u=ϕ(x) функция (a, b) интервалында анықталған, мәндер жиыны (с; d) интервал, y=f(u) функция (с; d) интервалында анықталған болып, бұл функциялар көмегімен y=f(ϕ(x) ) күрделі функция құрастырылған болсын.
Теорема. Егер u=ϕ(x) функцияның x∈(a, b) нүктеде туындысы, y=f(u) функцияның u=ϕ(x) нүктеде туындысы бар болса, онда y=f(ϕ(x) ) күрделі функцияның x нүктеде туындысы бар және
(f(ϕ(x) ) ) ’=f’(u) ⋅ϕ’(x) (1)
формула орынды болады.
Дәлелдеу. u=ϕ(x) функция x нүктеде туындысы бар болғандығы үшін оның x нүктедегі өсімшесін
∆u=ϕ’(x) ∆x+α(∆x) ∆x (2)
түрінде жазуға болады, бұл жерде ∆x→0 да α(∆x) →0.
Дәл солай, y=f(u) функцияның u нүктедегі өсімшесін
∆y=f’(u) ∆u+β(∆u) ∆u (3)
түрінде жазуға болады, мұнда ∆u→0 де β(∆u) →0.
Соңғы (3) теңдіктегі ∆u орнына оның (2) теңдікпен анықталған өрнегін қоямыз. Нәтижеде
∆y=f’(u) (ϕ’(x) ∆x+α(∆x) ∆x) +β((ϕ’(x) ∆x+α(∆x) ∆x) ) (ϕ’(x) ∆x+α(∆x) ∆x) =f’(u) ϕ’(x) ∆x +(f’(u) α(∆x) +ϕ’(x) β+α (∆x) β (ϕ’(x) ∆x+α(∆x) ∆x) ) ∆x
Теңдік келіп шығады.
Егер ∆x→0 болса, (2) теңдіктен α→0 және ∆u→0 болуы, егер ∆u→0 болса, онда (3) теңдіктен β→0 екендігі келіп шығады. Бұлардан ∆x→0 де f’(u) α+ϕ’(x) β+αβ шексіз аз функция екендігі келіп шығады, оны γ-мен белгілейміз.
Сонымен, ∆y=f’(u) ϕ’(x) ∆x+γ∆x теңдік орынды. Бұдан
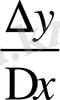 = f’(u) ϕ’(x) +γ және
= f’(u) ϕ’(x) +γ және
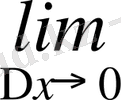
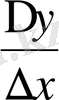 =f’(u) ϕ’(x) орынды екендігі келіп шығады. Бұл y’= f’(u) ϕ’(x) екендігін дәлелдейді.
=f’(u) ϕ’(x) орынды екендігі келіп шығады. Бұл y’= f’(u) ϕ’(x) екендігін дәлелдейді.
Мысал. y=
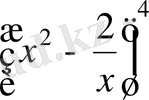 функцияның туындысын тап.
функцияның туындысын тап.
Шешу. Бұл жерде y=u
4
, u=
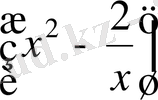 . Демек, y’=(u
4
) ’⋅
. Демек, y’=(u
4
) ’⋅
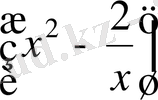 ’= =4u
3
’= =4u
3
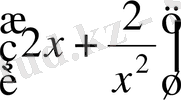 =8
=8
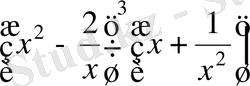 .
.
Әдетте (1) теңдікті
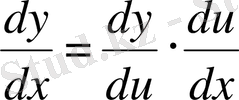 немесе y
x
’=y
u
’u
x
’
немесе y
x
’=y
u
’u
x
’
көріністе жазып, төмендегі ереже түрінде айтылады:
Күрделі функцияның тәуелсіз айнымалы бойынша, туындысы аралық айнымалы бойынша алынған туынды және аралық айнымалыдан тәуелсіз айнымалы бойынша алынған туындылар көбейтіндісіне тең.
Бұл ережені төмендегідей талқылауға болады: егер берілген нүктеде y айнымалы u-ге қатысты y u ’ есе жылдам, ал u болса x-ке қатысты u x ’ есе жылдам өзгерсе, онда y айнымалы x-ке қатысты y u ’u x ’ есе жылдам өзгереді, яғни y x ’=y u ’u x ’.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz