Шешім қабылдау есебі

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 55 бет
Таңдаулыға:

РЕФЕРАТ

Қазіргі қоғамның дамуы техникалық деңгейдің көтерілуімен, өндіріс құрылымын ұйымдастырудың күрделілігіне, жоспарлауды басқарудың әдістеріне қойылатын жоғарғы талаптармен сипатталады. Осындай жағджайда қоғамның экономикалық өркендеуін қамтамасыз ету үшін түрлі шешімдер қабылданады. Соңғы кезде тиімді шешім қабылдау теориясының пайда болуына осындай қажеттіліектер әсер етіп отыр. Бұл дипломдық жұмыс шешім қабылдау мәселелеріне арналған. Математикалық программалау, ойындар теориясы, жаппай қызмет көрсету немесе кезектер теорлиясы бсияқты күнделікті кездесетін нәрселерді қарастырғанда біз қандайда бір шешім қабылдаймыз. Демек қабылдаған шешімдердің тиімді болуын қарастыру өзекті мәселе. Негізінен мұндай есептерді үш кезеңге бөлуге болады:

экономикалық-математикалық модельді құру.
математикалық әдістердің бірін қолдана отырып тиімді шешімді табу.
алынған шешімді өндіріске енгізу.

Сондықтан бұл жұмыста әуелі шешім қабылдаудың кезеңдері баяндалады. Атап айтқанда мәселенің қойылуы, модельдер құру, шешім табу, модельді тексеру және шешімді бағалау, нәтижелерді енгізу сияқты ұғымдар келтірілген. Одан соң пайдалылықты өлшеудің жиы кездесетін әдістері: Фон-Нейман - моргенштерн, Черчмен - Акоф, сараптамалық бағалар, нысанка ағашы(В. М. Глушков) талданады. Шешім қабюылдаудың критерийлері көп болғандықтан, бас критерий, критерийлер үйірткісі, нормативті көрсеткіштер, «Идеалдар», біртіндеп өткізу, ымыраға келу секілді әдістердің қолданылуы кеңінен баяндалады. Осындай танымдардың негізінде қисындалған шешім қабылдау теориясы және оның практикада қолданылуын көрсетуге талпыныс жасалған.

Түйін сөздер: иерархия, тәуекел жағдайында шешім қабылдау, күтілетін мән, лаплас критерийі, Сэвидж критерийі, Гурвиц коритерийі, минимакс есептері.

Мазмұны

Кіріспе . . . 4

1. Шешім қабылдау есебінің кезеңдері . . . 6

1. 1. Мәселенің қойылуы . . . 6

1. 2. Моделдер құру . . . 6

1. 3. Шешім алу . . . 11

1. 4. Моделді тексеру және шешімді бағалау . . . 12

1. 5. Нәтижелерді енгізу . . . 13

2. Пайдалылықты өлшеу әдістері . . . 14

2. 1. Фон-Нейман Моргенштерн әдісі . . . 14

2. 2. Черчмен - Акоф әдісі . . . 15

2. 3. Сараптамалық бағалар әдісі . . . 16

2. 4. Нысана ағашы (В. М. Глушков) әдісі . . . 20

3. Көп критерийлі есептер . . . 22

3. 1. Бас критерий әдісі . . . 23

3. 2. Критерийлер үйірткісі . . . 23

3. 3. Нормативті көрсеткіштер . . . 24

3. 4. «Идеалдар» әдісі . . . 24

3. 5. Біртіндеп өткізу әдісі . . . 24

3. 6. Ымыра әдісі (Â. Парето) . . . 25

4. Шешім қабылдау теориясы және оны практикада қолдану . . . 26

4. 1. Анықталғандық шартында шешім қабылдау - иерархияға анализ жасау әдісі . . . 27

4. 2. Тәуекел жағдайында шешім қабылдау . . . 38

4. 2. 1. Күтілетін мән критерийі . . . 38

4. 2. 2. Күтілетін мәннің басқа критерийлері . . . 41

4. 3. Анықталмағандық жағдайында шешім қабылдаудың оңтайлы

ұстаным критерийлері . . . 48

Қорытынды . . . 54

Пайдаланылған әдебиеттер тізімі . . . 55

КІРІСПЕ

Қазіргі таңда адамзат қызметінің барлық аясында белгілі бір мақсатқа жету үшін түрлі шешім қабылдау кезінде операцияларды зерттеу теориясы негізгі құрал болып табылады. Бұл теорияның қайнар көзі - математикалық моделдеу.

Мәселен қайбір шаруамен сіз өзіңіз тұратын қаладан басқа қалаға бес апта бойы барып тұруыңыз керек болсын делік. Ол қалада Сіз алғаш рет бірінші аптаның дүйсенбісінде болып, өз қалаңызға бесінші аптаның сәрсенбісінде ақырғы рет оралуыңыз қажет. Билет құны 400 доллар. Дегенмен, аптаның аяғында ұшатын болсаңыз, сізге 20 пайыз жеңілдік жасалады. Мұның сыртында бір бағыттағы билеттің құны тапсырыс берілген билет құнының 75 пайызына тең. Әрине, сіз жол шығынын азайтқыңыз келеді. Бұл жағдайды тиімді таңдау жасау үшін негізгі үш компонентті анықтауды қажет ететін шешім қабылдау есебі ретінде қарастыруға болады:

1. Бұл жағдайдлағы альтернатив шешім деп нені қабылдаймыз?

2. Мүмкін болатын шешім қандай шектеулерді қанағаттандыруы қажет?

3. Алтернатив шешім қандай критерий бойынша қабылданады?

Егер Сіз тұратын қаланы А деп, ал баратын қалаңызды В деп белгілесек, бұл есепте келесі альтернативтер орын алар еді:

1. А-В-А бағытында тапсырыспен бес билет сактып алу (яғни А-дан В-ға және кері бағытта) ;

2. А-В бағытында бір билет, аптаның аяғына сай келетін А-В-А бағытында төрт билет және «бір бағыттағы» В-А билетін сатып алу;

3. Бірінші апта үшін ішінде дүйсенбісі бар күндерді қамтитын А-В-А билетін сатып алу; соңғы апта үшін сәрсенбіні қамтитын А-В-А билетін алу.

Мұндағы бірінші және соңғы билеттер аптаның соңғы күндеріне сай болуы керек. Сол сияқты А-В-А төрт билетінде де аптаның соңғы күні қамтылуы қажет.

Берілген есептегі шектеулер бірінші аптада дүйсенбі күні В қаласында болуды, А қаласында соңғы аптаның сәрсенбісінде болуды білдіреді.

Бұл жағдайдағы мүмкін альтернативтерді бағалаудың критерийі - билет бағасы. Берілген жағдайда келісі варианттар алынады:

1-альтернатив: билет бағасы =5х400=2000 доллар;

2-альтернатив: билет бағасы =0, 785х400+4х0, 8х400 +0, 75х400=1800 доллар;

3-альтернатив: билет бағасы =5х(0, 8х400) =1600 доллар.

Осыдан ең жақсы альтернатив үшінші екенін көреміз. Жалпы жағдайда математикалық моделдер құрудың алғашқы қадамы альтернативтерді немесе шешімдер айнымалысын анықтау болып табылады.

Шешім қабылдау теориясында бірнеше ықтимал альтернативтер арасынан ең жақсысын таңдаудың «көкейге қонымды» процедурасы қолданылады. Таңдаудың қаншалықты дұрыс болатындығы шешім қабылданған жағдайды бейнелегенде қолданылатын мәліметтердің сапасына тәуелді. Осы тұрғыдан алғанда шешім қабылдау процесі келесі үш шарттың біріне тиісті болады:

1. Мәліметтер дәл белгілі болғандағы, яғни анықталғандық жағдайындағы шешім қабылдау.

2. Мәліметтерді ықтималдықты үлестірімдер арқылы өрнектеуге болады, яғни тәуекел жағдайында шешім қабылдау.

3. Шешім қабылдау процесінде маңыздылығының дәрежесін мәліметтерге салыстырмалы салмақтарды(салмақ коэффиценттерін) жазуға болмайтын, яғни анықталмағандық жағдайында шешім қабылдау.

Нақтысында, анықталғандық шартында мәліметтер сенімді анықталған, ал анықталмағандық кезінде олар толық анықталмаған, тәуекел жағдайында шешім қабылдау “аралық” кезеңді білдіреді.

1. Шешім қабылдау есебінің кезеңдері

1. 1. Мәселенің қойылуы

Қолында түрлі стратегиялар (яғни басқарылатын айнымалылардың мәндері) бар шешім қабылдаушы кісі әрбір стратегияны қабылдағанда қайбір дәрежедегі өз мақсатына сай келетін түрлі нәтижелерді алады. Таңдалатын стратегияның әсерлілігіне қоршаған орта шарттары - басқарылмайтын айнымалылар - ықпал етеді.

Операцияларды зерттеу мәселелерін қойғанда шешім қабылдаушы кісілердің тобын анықтап, маңызды айнымалаларды атап көрсетіп, оларды басқарылатын айнымалылар (стратегиялар) мен басқарылмайтын айнымалыларға (қоршаған орта шарттарына) жіктеп, жүйенің қызмет ету мақсатын қисындаймыз. Сонымен, біз шешім қабылдау 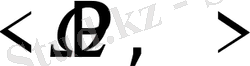есебіне тірелеміз. Мұндағы - альтернативтердің (нұсқалардың) әуелгі жиыны, - қайбір ішкі жиынын бөліп алуға көмектесетін тиімділік принципі (дербес жағдайда, жалғыз элементтен тұруы да мүмкін) . Бұдан әрі ішкі жиынынан шешім қабылдаушының көзқарасы бойынша қабылдауға тұрарлық ең жақсы саналатын қандайда бір шешім таңдалады. Шешім қабылдаудың жалпы есебінде нұсқалар жиыны мен тиімділік принципі алдын ала берілмеуі де мүмкін. Есепте берілсе, онда есеп таңдау есебі делінеді де, ал мен 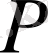берілсе - тиімділеу есебін аламыз. Практикалық есептерде нұсқалары түрлі x қасиеттердің жиынтығын сипаттайды. x нұсқасын бағалау үшін 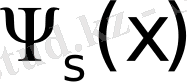векторы енгізіледі, мұндағы 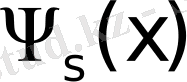дегеніміз x нұсқасының 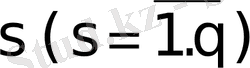қасиеті бойынша сандық бағалануы. Бұдан соң осы бағалаулар негізінде тиімділік принципі қалыптасады.

1. 2. Моделдер құру

Операцияларды зерттеуде нақтылықты өрнектейтін моделдер айрықша рөл атқарады. Олар өздері бейнелейтін жүйелердің айқын да ықшам кескінін алуға мүмкіндік береді. Көбіне моделдерді талдап, эксперимент жасап, қарастырылатын жүйедегі өзгерістің жүйе қызметінің сапасына ықпалын анықтайды. Осындай әдістердің арқасында жүйенің өзіне тікелей эксперимент жасау қажеттілігінен құтыламыз. Кейде, жүйеде натура-эксперимент өткізу мүмкін емес, немесе оған мол қаржы мен уақыт қажет болады. Әдетте, обьектіні жасағаннан гөрі оның әлдеқайда қарапайым моделін жасаудың сәті түседі. Қандай да бір құбылысты тап басып, дәл айту үшін қыруар айнымалы қажет болса да, оның негізгі қасиеттерін анықтауға айнымалылардың салыстармалы түрде кішігірім сандары жеткілікті. Тек, анағұрлым маңызды айнымалыларды таңдау, олардың арасындағы байланысты дәл бейнелеу және жүйе қызметінің мақсатын дұрыс қиыстыру оңайға түспейтіндігі де белгілі.

Операцияларды зерттеуде қолданылатын моделдердің типіне тоқталсақ:

1) кескіндеуші,

2) аналогты,

3) символды,

4) имитациялық.

Кескіндеуші моделдер нақты обьектіге сырттай ұқсас болғанымен, одан өлшемдері өзгеше, яғни обьектінің бейнесі мен көшірмесін білдіреді. Анағұрлым көбірек таралған осындай типтегі моделдер: суреттер, сызбалар, эскиздер, фотографиялар, ұлғайтылған немесе кішірейтілген моделдер және т. б. Автомобилдерді, станоктарды, мебелдерді конструкциялау процесінде бұйымның жалпы көрнісі мен деталдерінің өлшемдері көрсетілген сызбалар жиі қолданылады. Киім пішкенде матаны пішу схемалары мен эскиздері пайдаланылады. Жаңа ұшақ конструкциясының аэродинамикалық қасиеттері алдын ала аэродинамикалық құбырдағы кішірейтілген натура-моделде зерттеледі. Кемелердің гидродинамикалық сипаттары оның натура-моделдерін бассейнде сынау арқылы анықталады.

Аналогты моделдерде бір қасиеттер топтамасы екінші мүлде басқа бір қасиеттер тобын бейнелеу үшін қолданылады. Мысалы, гидравликалық жүйені электрлік, транспорттық немесе экономикалық жүйелер аналогы ретінде қолданады. Тұтқыр ортадағы математикалық маятниктің өшпелі тербелісі конденсатордан, индуктивтіліктен және резистордан тұратын электрлік схема арқылы моделденеді, бұл жағдайда маятниктің механикалық қозғалысының аналогы - конденсатор қабаттарындағы кернеулердің өзгеруі, тұтқыр орта аналогы - резистор кедергісі.

Символды моделдерде объектінің бейнеленуі шартты символдар арқылы жүзеге асады. Мысалы, хатты әліппи қаріптері арқылы жазсақ, музыкалық шығармаға нота қолданамыз. Егер, моделдеу процесінде математикалық символдар (арифметикалық және логикалық амалдар; теңдік, теңсіздік, функционалдық тәуелділіктер, туындылар мен интегралдар, алгебралық және дифференциалдық һәм интегро-дифференциалдық теңдеулер т. б. ) пайдаланылса, онда математикалық моделді аламыз. Операцияны зерттеу есептерін шығаруда математикалық моделдер маңдай алды орында екендігін атап өткен жөн. Дегенмен, ұйымдық басқару есебін шығару әрдайым математикалық моделдер құруға және тиісті есептеулер жасауға соқтыра бермейді. Бұл, дербес жағдайда, шешім қабылдау барысында қойылған есепті басқарушының дұрыс шешуінде маңызды рөл атқаратын, бірақ қатаң қисындауға көне бермейтін (демек математикалық моделге тікелей ене алмайтын) факторлармен жиі үшырасатындығымыздан көрінеді. Осындай қиысуы қиын факторлардың бірі - адамзат қызметінің «бихевиоралді» делінетін (behaviour - мінез-құлық сөзінен шыққан) факторы.

Математикалық моделдеудің қолданыс аясы қанша кең болғса да, ұйымдық басқарудың көптеген маңызды есебін қарастырғанда талдаудың мүлде басқа әдістеріне көңіл бөлу қажеттігі туады. Мәселен, математикалық моделдерді сандық шешу үшін шағын өлшемді жүйелер жағдайымен шектеліп, зерттелінетін обьекті құрылымына және олардың қызмет ету алгоритмдеріне қатысты ықшамдаушы ұйғарымдар жасауға тура келеді . Бұл кездегі алынған моделдер нақты жүйедегі өтетін процестердің қарабайыр жуықтауы болып қалуы мүмкін. Мұндайда жүйе қалпын компьютерде «айнытпай бейнелеуге» (имитациялауға) мумкіндік беретін имитациялық моделдерді қолданамыз. Имитациялық моделдеуде:

айнымалылар арасындағы қайбір функционалдық тәуелділіктерді кестелер немесе математикалық күрделі функциялар көмегімен ескере аламыз; анықталмаған факторларды да ескеруге, сонымен қатар үлестірім заңы кестелер немесе күрделі математикалық функциялар арқылы берілетін кездейсоқ шамаларды генерациялауға да мүмкіндік бар; жүйенің қызмет етуінің күрделі алгоритмдерінің программалай аламыз.

Сонымен, математикалық модел құрып, шешімін алу мүмкін емес жүйелердің қалпын имитациялауға мүмкіндік аламыз. Мұның сыртында имитациялық моделдер жүйені неғұрлым дәл бейнелеуге ықтияр береді. Имитациялық моделдеудің негізгі кемшілігі - көптеген эксперимент қажеттігі, экспериментті жоспарлау және бақылау нәтижелерін статистикалық өңдеу қиындықтары .

Моделдеу принциптері. Моделдің сапасы операциялық топтардың творчестволық қабілетіне аса тәуелді. Сондықтан, нақты операцияны зерттеу есептерінің моделдерін құру шеберлігіне бүкіл үміткерлерді үйрететін нұсқау беру мүмкін емес. Моделдер құрудан жинақталған тәжірибелерге сүйеніп, ой өрісті кеңейтетін және творчестволық ізденіс бағытын тура таңдауға септігі тиетін кебір принциптерді атап кетелік:

1) Жүйе қызметіне тікелей талдау жасау. Бұл жүйе құрылымы мейлінше қарапайым кезінде, жүйені тексеріп барып, оны бейнелей алатын жүйе қызметінің заңдылықтары белгілі болғанда қолданылады.

2) Аналогты пайдалану . Мұны жүйенің құрылымы мейлінше айқын болғанымен, оны математикалық бейнелеу тәсілі ұғынықсыз жағдайда, ал кейде қарастырылып отырған жүйенің өзінен құрылымы анағұрлым қарапайым аналогиялық жүйемен ұқсастығын іске асыруға болатын ахуалдарда пайдаланамыз.

3) Мәліметтерді талдау («жұмбақ жәшік» принципі) . Жүйе құрылымы айқын болмағанда оны жүйенің қызметін сипаттайтын мәліметтерге сүйеніп бейнелеуге тырысамыз. Жүйе құрылымы туралы қалыптасқан гипотеза негізінде осы гипотеза құрылған мәліметтермен сай келмейтін басқа эксперименттік мәліметтерді пайдаланып тексеру қажет. Физика, химия, астрономия және басқа ғылым салаларындағы көптеген іргелі заңдар әуелі эксперименттік мәліметтер мен бақылау нәтижелеріне талдау жасау арқасында дүниеге келгені мәлім.

4) Жүйеге эксперимент жасау . Маңызды айнымалыларды айыруға, жекеленген айнымалылардың жүйе жұмысының сипатына ықпалын анықтауға мәліметтерге талдау жасау мүмкіндік бермегенде натура-эксперимент жүргізу қажеттігі шығады.

5) «Жасанды нақтылықты» қолдану. Жүйені сипаттаушы мәліметтер жоқ, немесе оларды алу мүмкін емес кезде, ал жүйеге эксперимент жасау ұзақ уақытты қалайтын немесе қымбатқа түсетін, кейде мүлде мүмкін емес, жағдайларда ең қиын ахуалға тап боламыз. Мысалы, әлеуметтік ірі дау-дамайдың дамуын бақылауға мүмкіндік беретін әдістерді анықтау мақсатында зерттеулер жүргізу қажет болсын. Мұндай жағдайларға сандық талдау жасауға қажетті мәліметтер жоқ, оларды ешқайдан да ала алмаймыз. Бұл салада эксперимент жүргізуге қоғамның келіспейтіндігі айдан анық. Осындай ахуалдардың құрамы туралы ешқашан ешқандай ұсыныс болған емес. Мұндай дау-дамайдың моделін құруға қалай кірісер едік? Бәрінен бұрын, зерттелетін жүйенің қасиеттері мен құрылымына қатысты пайдаланылатын көптеген гипотезаларды тексеретін, «жасанды нақтылықты» моделдейтін күрделі эксперименттік ахуал құрастырылады. «Жасанды нақтылық» нағыз нақтылықтың моделі емес, моделдеуге болатын нақтылық ретінде қолданылады. Ол статистикалық жинақ (тәжірибе жинау) үшін пайдаланылады. Ахуалды бірқатар қарапайым эксперименттік ахуалдарға бөлшектеу (декомпозиция) мүмкіндігі болуы тиіс. Әр қарапайым ахуал үшін дербес «микро»-теориялар (мысалы, антагонистік ойындарды қолданып екі кісі дауының моделдері) жасалады да, осылайша алынған моделді жасанды нақтылықтың тұтас моделіне жалпылауға әрекеттенеміз. Мұнымен бірге осы жасанды нақтылықта жиналған статистиканың тікелей макро-талдамының көмегімен «жасанды нақтылықты» теориясын жасауға талпынамыз.

Моделдер құрудың осы екі бағыты «жасанды нақтылықтың» қайбір қанағаттанарлық ( 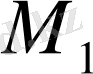) моделі алынғанша өзара байланыста жүзеге асады.

1-сурет. «Жасанды нақтылықты» қолданып моделдеу.

Одан соң «жасанды нақтылық» түрлендіріледі де, әуелде алынған 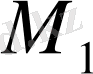моделін жалпылау нәтижесінде анағұрлым жалпы 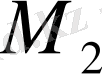моделі алынады. Осылайша күрделіленген сайын жалпылана түсетін моделдер тізбегі 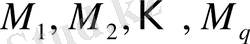қалыптасады (1. 2. 1-сурет) .

Нақтылықты ықшамдау әдістері. Операцияны зерттеудің нақты есептерінің математикалық моделдерің құрумен айналысатын операционист-ғалымдар алдында қарама-қайшы екі мақсат бар. Бір жағынан модель толық, яғни онда операцияның нәтижесі тәуелді болатын барлық маңызды факторлар ескерілуі керек, ал екінші жағынан модель белгілі математикалық әдістерді қолданып тиімді шешім аларлықтай мейлінше қарапайым болғаны дұрыс.

Көптеген қосалқы ұсақ факторларды ескеру моделдің математикалық талдамын қиындатып жібереді де, шешім табылғанның өзінде ол шешімнің ақылға сыйуы қиын. Демек, моделді құрғанда нақтылықты елестету дәлдігіне айтарлықтай нұқсан келтірмей ықшамдаған жөн.

Нақтылық келесі әдістермен ықшамдалады:

1) Айнымалыларды жою . Жүйедегі айтарлықтай ықпалды айнымалалардан айырылуға болмайды, ендеше қайбір айнымалыларды жоюдың нағыз қатаң талдауға негізделгені ләзім.

2) Айнымалылар табиғатын өзгерту (болмашы өзгеретін айнымалыларды константаға, дискретті айнымалыларды үзіліссізге, үзіліссіз айнымалыны дискреттіге, кездейсоқ шаманы оның математикалық күтіміне алмастыру т. с. с. ) .

3) Айнымалылар арасындағы функционалдық қатынастарды өзгерту (сызықтық емес функцияларды сызықтық аппроксимациялау, сызықтық еместікті құрақты-сызықты функциямен алмастыру, көпмүшеліктер мен тригонометриялық функциялар арқылы интерполяциялау және аппроксимациялау, дискретті (биномдық, пуассондық) үлестірім функцияларын үлестірімнің үзіліссіз нормалдік заңдарымен аппроксимациялау т. с. с. )

4) Шектеулерді өзгерту ( шектеулерді қосу, жою немесе түрлендіру) .

1. 3. Шешім алу

Шешім қабылдау процесінің ең жалпы математикалық моделі мына түрде болады:

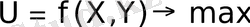(1. 1)

мұнда 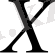- басқарылатын айнымалылар, 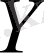- басқарылмайтын айнымалылар, - пайдалылық функциясы. Мұның сыртында, моделге шартты түрде төмендегіше жазылатын шектеулер енеді.

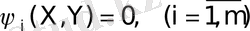(1. 2. )

Осы (1. 1) мақсат функциясын минимумдайтын, берілген (1. 2) шектеулерін қанағаттандыратын, 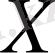- басқарылатын айнымалылар векторын анықтау қажет. Тиімді шешімді іздеуге математикалық программалаудың түрлі (сызықтық, дөңес, сызықтық емес, динамикалық, дискретті, стохастикалық т. б. ) әдістері қолданылады. - мақсат функциясының күрделі түрде болуы, айнымалылар мен шектеулердің көптігінен экстеремалдік есептерді шешудің классикалық әдістері қолдануға жарамай қалуы жиі ұшырасады. Мұндайда итерациялық әдістерді қолдануға мәжбүрміз. Бұл әдістің мәнісі - есептеу процесі (1. 2) облысындағы қайбір ұйғарымды шешімнен басталады да соңына (1. 1) мақсат функциясы мәнінің жақсаруын қамтамасыз ететін алгоритм қолданылады. Бұдан арғы жақсару мардымсыз екендігіне немесе әрі қарай есептеу «құны» мейлінше қымбаттығына көзіміз жеткенше процесс жалғаса береді.

Моделді тексеру және шешімді бағалау

Моделдің нақты шындыққа адекваттығын тағайындау және моделдегі кемшіліктерді түзеу мақсатында моделге тексеру жүргізіледі. Аталған кемшіліктер қатарына жататындар:

1) Модель маңызсыз айнымалылырды қамтиды;

2) Модель кейбір маңызды айнымалыларды қамти алмайды;

3) Кейбір маңызды айнымалы мәндеріне дәлдігі жеткіліксіз баға жасалған;

4) Моделдің құрылымы жалған.

Аталған кемшіліктерді аңғаруға көбіне статистикалық әдістер қолданылады.

Көптеген операцияны зерттеу есептерінде таңдалған тиімділік критерийіне біреулерінің ықпалы айтарлықтай, ал екіншілерінікі - мейлінше мардымсыз айнымалылар жиі кездеседі. Операционист қыруар айнымалылар арасынан ең маңыздысын таңдап, айнымалылардың аз мөлшерін қамтитын, адекватты моделді құруға ұмтылғаны жөн. Айнымалының тиімділік критерийіне ықпалының дәрежесін анықтайтын статистикалық әдістер: корреляциялық талдам мен регрессиялық талдам, сондай-ақ дисперсия мен ковариация талдамдары.

Қайбір шамасының мәнін бағалау үшін негізінде бағасы есептелінетін өлшемдері жүргізіледі. Сұрыптау арқылы бағалаудың жалпы үш әдісі бар: Пирсонның моменттер әдісі, Фишердің максимум шындыққа жанасым әдісі және Байес әдісі.

Өзі жалған функционалдық тәуелділіктерді қамтығандықтан, моделіміз қанағаттанарлықсыз болуы да мүмкін. Қолдағы эмпирикалық мәліметтерге мағанасы сай келетін тиімді функцияны таңдаудың қандай да бір жүйелік әдісі жоқ. Таңдау, әдетте, айнымалылар арасындағы қатынастар немесе қайбір кесімдер арқылы жүргізіледі. Зерттеуші сан алуан функционалдық тәуелділіктен хабардар болған сайын оның таңдауы әлдене түседі. Функция таңдалғандағы айнымалыларды пайдаланып функцияның бақылау мәліметтерімен беттесуін тексере алмаймыз. Моделдің нақты жүйеге адекваттылығын бағалау гипотезаларды статистикалық тексеру әдісімен жүзеге асады. Сонымен қатар, шешімді оның параметрлерінің өзгеруіне, өлшеу қателіктеріне т. с. с. сезімталдықтарына талдау жасау арқылы да бағалау қажет.

Нәтижелерді енгізу

Операцияны зерттеудің мақсаты - ұйымдық басқару жүйесі қызметінің көрсеткіштерін жетілдіру. Оған мына шарттарда ғана жете аламыз:

1) Уәкілдігі мінсіз бастық операциялық зерттеулер нәтижесінде табылған шешімді құптап, бекітеді;

2) Бұл шешім дұрыс жүзеге асады (енгізіледі) ;

3) Жүйе мен сыртқы орта қалай өзгерсе де шешімнің ұтымдылығы сақталады.

Жауапты басшының ұсынылған шешімді құптауы оның бұл шешімнің мәнісін қай деңгейде зерделегендігіне, сонымен қатар шешім алған әдісті қалай ұққандығына байланысты. Мұндай түсіністікке жету өз кезегінде басшының жеке басының операциялық зерттеулер процесіне қатынасу дәрежесіне тәуелді. Зерттеу жүргізу барысында туындаған сұрақтарды талқылау мен кеңес алу мақсатына мүдделі барлық басшылармен операционист-ғалым жеке кездесуі керек. Сондай-ақ барлық мүдделі басшылармен тұрақты түрдегі жұмыс- кеңестерін ұйымдастыруы қажет.

Алынған нәтижелерді енгізуге операционист-ғалымның қатысуы міндетті. Шешімді енгізу шағында зерттеу кезеңдерінде ойластырылмаған мәселелердің туындауы - заңды құбылыс. Сондықтан, алынған шешім жетілдіруді талап етіледі. Операционист осы шешімді жүзеге асыратындарға арнап бақайшағына дейін тәптіштелген нұсқау беруі қажет. Енгізу жоспарын жасауға тек басшылар (жоғары басшылық пен басқарудың төменгі буындарын) ғана емес, енгізілетін шешімге қатысы бар бүкіл кісілер қатыстырылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.