Ықтималдық теориясы мен математикалық статистиканың элементтері: мысалдар мен есептер


ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫ ЖӘНЕ МАТЕМАТИКАЛЫҚ СТАТИСТИКА ЭЛЕМЕНТТЕРІ
Кездейсоқ оқиғалар
Бірінші мысал. Қорапта 4ақ, 9 қара және 7 қызыл бірдей шарлар салынған. Қораптан кез-келген бір шар алынады. Сонда ақ шар пайда болуының ықтималдылығы қандай?
Шешуі: А-ақ шар пайда болуы болсын. Бұл тәжірибеде элементарлық оқиға дегеніміз қораптан кез-келген бір шар алу. Шарлар бірдей болғандықтан бұл оқиғалар тең мүмкінді және өзара үйлесімсіз. Элементарлық оқиғалардың жалпы саны осы қораптағы шарлар санына тең n=20, ал А оқиғасына қолайлы элементарлық оқиғалар саны қораптағы ақ шарлар санына тең. Сондықтан ықтималдықтың анықтамасы бойынша
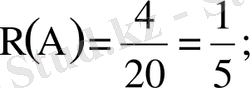
Екінші мысал:а:
а) Ө, Н, С, Е, Д, У әріптері бөлек карталарға жазылған. Содан кейін карталар араластырып кез-келген ретпен бір қатарға орналастырылған. Сонда сәндеу сөзінің пайда болуының ықтималдығы қандай?
б) Әрқайсысында бір әріп жазылған карталардан “Жарлық”сөзі құрылған. Карталарды араластырып, содан кейін бір-бірлеп алған ретімен сөз құрастырылады. Сонда ЖАҚ сөзінің пайда болуының ықтималдығы қандай?
Шешуі: а) Берілген алты карталардың бір қатарға әртүрлі орналасуларының бір-бірімен айырмашылығы олардың қандай ретпен орналасқандығында болады. Сондықтан ондай орналасулардың жалпы саны мына формуламен анықталады, яғни
n=
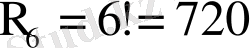
Берілген алты картаның әрбір орналасу комбинацияларын оқиға ретінде қарастырсақ, онда олар тең мүмкінді, үйлесімсіз оқиғалар болады. Ал бізге қолайлы элементарлық оқиғалар саны m=1.
Себебі карталар әртүрлі комбинациямен орналасқанда “Сәндеу” сөзі бір-ақ рет кезігеді. Сонда
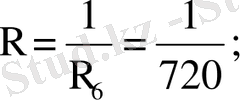
б) Берілген алты карталардан үш карта бойынша орналастырулар саны n=
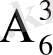 . Ал үш әріптен тұратын комбинациялардың бізге керегі біреу-ақ, яғни ЖАҚ, олай болса m=1. Сөитіп
. Ал үш әріптен тұратын комбинациялардың бізге керегі біреу-ақ, яғни ЖАҚ, олай болса m=1. Сөитіп
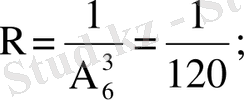
Үшінші мысал. Ұйымда 6 ер адам, 4 әйел адам жұмыс істейді. Табельдегі нөмірлері бойынша 7 адам таңдап алынды. Таңдап алынған адамдардың ішінде 3 әйел бар болуының ықтималдығын табу керек.
Шешуі: Табельдегі нөмірлері бойынша барлығы 10 адамнан 7 адам таңдап алудың жалпы саны 10 элементтен 7 элемент бойынша алынған терулер саны сияқты есептелінеді, яғни
n=
Ал 3 әйелді табельдік нөмерлері бойынша 4 әйелдің ішінен таңдап алудың саны
m
 =C
=C
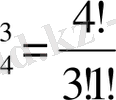
Сондай-ақ 6 ер адамнан 4 ер адам таңдаудың саны
m
 =C
=C
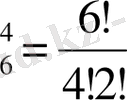
Енді көбейту ережесін пайдалансақ таңдап алынған 7 адамның ішінде 3 әйел 4 ер адам болу мүмліндіктерінің жалпы саны
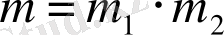 тең.
тең.
Сонымен анықталғалы отырған ықтималдық
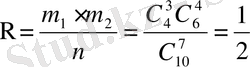
Бұдан былай ықтималдықтың анықтамасын пайдаланып есептер шығарғанда, әуелі оқиғаны белгілі бір әріп арқылы белгілеп алу қажет. Содан кейін тең мүмкінді, үйлесімсіз элементарлық оқиғалардың жалпы санын, сосын қолайлы элементарлық оқиғалар санын есептеген жөн.
Төртінші мысал: Кітап сөресінде кездейсоқ ретпен 5 томнан тұратын анықтама қойылған:
а) кітаптар бірінші томнан бесінші томға дейін дұрыс ретпен орналасуының ықтималдығын табу керек;
б) ең болмағанда бір томның ретті орнында тұрмаған жағдайдың ықтималдығын табу керек.
Шешуі: Сынақ ретінде кітап сөресінде кітаптардың кез-келген ретпен қойылуын қарастырайық. Сонда кітаптардың бұлай орналасуларының жалпы саны
n=P
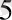 =5!=120
=5!=120
1) А әріпі арқылы кітап сөресінде кітаптардың том нөмірлерінің өсу ретімен орналасуын білдіретін оқиғаны белгілейік. Бұл оқиғаға қолайлы элементарлық оқиға біреу-ақ.
Сондықтан
P(A) =
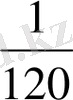
2) В әріпі арқылы, ең болмағанда бір том ретті орнында болмауын білдіретін оқиғаны белгілейік. Мұндай оқиғалар саны m=n-1, яғни m=119. Себебі кітаптардың том нөмірлері бойынша дұрыс орналасуы бірге тең, ал қалған орналасулар В оқиғасын анықтайды. Сонымен Р(В) =119/120;
Осы жерде А мен В оқиғаларының қарама-қарсы екенін ескерсек, онда Р(А) +Р(
 ) =1 екенін пайдаланып
) =1 екенін пайдаланып
Р(В) =1-Р(А) =1-
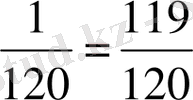 табамыз, яғни бұрынғы жауапты алдық.
табамыз, яғни бұрынғы жауапты алдық.
Бесінші мысал. Қорапта бірдей 5 бұйым бар. Оның үшеуі боялған. Қораптан кез-келген екі бұйым алынды:
1) алынған екі бұйымның біреуі боялған бұйым болуының ықтималдығын табу керек;
2) алынған бұйымның екеуі де боялған бұйым болуының ықтималдығын табу керек.
Шешуі:
1) қорапта 5 бұйымның екеуін барлығы n=C
 тәсілмен алуға болады, ал алынған екі бұйымның біреуі боялған болса, сол бір боялған, бір боялмаған бұйымдарды сәйкес m
тәсілмен алуға болады, ал алынған екі бұйымның біреуі боялған болса, сол бір боялған, бір боялмаған бұйымдарды сәйкес m
 =C
=C
 m
m
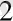 =C
=C
 тәсілмен алуға болады. Сонда екі бұйымның бірі боялған болудың барлық қолайлы элементарлық оқиғалар саны
тәсілмен алуға болады. Сонда екі бұйымның бірі боялған болудың барлық қолайлы элементарлық оқиғалар саны
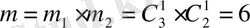
Сөйтіп Р=
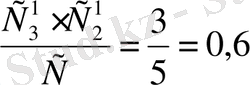
2) алдыңғы пунктегі шығару жолын пайдаланып
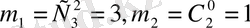
Сонда
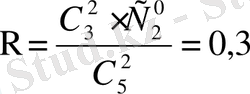
Алтыншы мысал. Екі 4 және 5 цифрларының көмегімен әртүрлі үш орынды қанша сан жазуға болады?
Шешуі: Барлығы екі 4 және 5 цифрлары берілгендіктен іздеп отырған комбинацияларды бірден жазуға болады: 444, 445, 454, 544, 555, 554, 545, 544 барлығы 8 сан болады. Ал осы жауапты қайталанбалы орналастыруды пайдаланып та алуға болады.
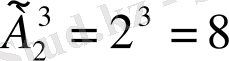
Жауабы: Барлығы 8 сан жазуға болады.
Жетінші мысал. Мына 5; 3; 1; 5; 5; 1 цифрлардың көмегімен алты таңбалы қанша сан жазуға болады.
Шешуі: Берілген алты цифрды үш группаға бөлеміз: 1; 1, 3; 5, 5; 5.
Есептің шартына қайталанбалы алмастырулар формуласын пайдалануға болады.
Сонда
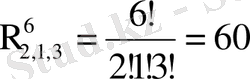
Жауабы: Барлығы 60 сан жазуға болады.
Сегізінші мысал. Гүл дүкенінде 3 түрлі гүлдер бар. Алынған 7 гүлден қанша әдіспен букет жасауға болады?
Шешуі: Сатып алынған гүл саны 7-ге тең. Сондықтан жасалған букет 7 гүлден тұрады. Ал осы букетке үш түсті гүлдердің әрбір түсінен бірнеше гүл кіруі мүмкін. Олай болса қайталанбалы терулер формуласын пайдаланып
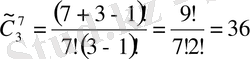
Жауабы: 36 әдіспен букет жасауға болады.
Тоғызыншы мысал. 1-ден 35-ке дейінгі бүтін сандар арқылы нөмірленген 35 емтихан билеттерінің ішінен қалай болса солай бір билет алынған. Суырылған билеттің нөмірі үшке еселі сан болу ықтималдығы қандай?
Шешуі: Тәжірибеміз - бір билет алу. Билет қалай болса солай суырылғандықтан тәжірибенің барлық нәтижелері тең ықтималды және оның үстіне, олар қиылыспайды. Тәжірибенің мүмкін нәтижелерінің саны 35-ке тең. А оқиғасы алынған билеттің нөмірі үшке еселі болатындығын көрсетеді. Бұл оқиғаға тәжірибенің 11 нәтижесі қолайлы болады.
{3; 6; …; 33}. Демек, ізделінді ықтималдық тең
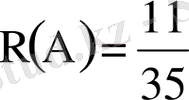
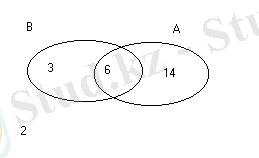 Оныншы мысал. Эйлер-Венн диаграммасы.
Оныншы мысал. Эйлер-Венн диаграммасы.
Группадағы 25 студенттің 20-сы спортсмен, (А оқиғасы), 9-ы музыкамен (Воқиғасы), 6-ы музыкамен және спортпен (АВ оқиғасы) . Эйлер-Венн диаграммасын құрып,
 ,
,
 ,
,
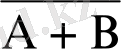 оқиғаларының не білдіретіндігін көрсетелік.
оқиғаларының не білдіретіндігін көрсетелік.
Шешу:
Эйлер-Венн диаграммасын құрамыз. Дөңгелектер А мен В оқиғаларын, дөңгелектердің қиылысуы АВ оқиғасын көрсетеді. Дөңгелектердің қиылысуына музыка және спортпен айналысатын студенттердің саны сәйкес келеді, яғни 6 адам.
 және
және
 оқиғалары, бұларға сәйкес, 14 студенттің тек спортсмен, ал 3 студент тек музыкамен айналысатындығын көрсетеді. Демек музыкамен немесе спортпен 23 студент айналысады, сондықтан да
оқиғалары, бұларға сәйкес, 14 студенттің тек спортсмен, ал 3 студент тек музыкамен айналысатындығын көрсетеді. Демек музыкамен немесе спортпен 23 студент айналысады, сондықтан да
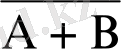 оқиғасы студенттердің ішінде тек екеуінің мұндай әуестенуі жоқтығын көрсетеді.
оқиғасы студенттердің ішінде тек екеуінің мұндай әуестенуі жоқтығын көрсетеді.
Студенттерге өзіндік есептер
1. Үш тиын лақтырылып тәжірибе жүргізілсін. Сонда С
 , С
, С
 және С
және С
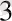 бірінші, екінші және үшінші тиындардың сәйкес сан жазылған жақтарының пайда болуын білдіретін оқиғалар болсын.
бірінші, екінші және үшінші тиындардың сәйкес сан жазылған жақтарының пайда болуын білдіретін оқиғалар болсын.
Енді С
 (i=1, 3) арқылы мына оқиғаларды өрнекте: А-бір сан жазылған жақтың, екі елтаңба жазылған жақтардың пайда болуы;
(i=1, 3) арқылы мына оқиғаларды өрнекте: А-бір сан жазылған жақтың, екі елтаңба жазылған жақтардың пайда болуы;
В-бір реттен артық елтаңба жазылған жақтардың пайда болмауы;
С-үш елтаңба жазылған жақтардың пайда болуы.
Д-үш сан жазылған жақтардың пайда болуы.
2. Мына оқиғаның ақиқат оқиға екенін дәлелде
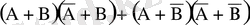
3. Өрнекті ықшамда:
а)
 в)
в)
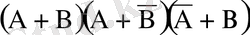
4. Төмендегі оқиғалар группалары толық группалар бола ма?
а) А
 -тиынның сан жазылған жағы
-тиынның сан жазылған жағы
А
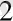 -тиынның елтаңба жазылған жағы
-тиынның елтаңба жазылған жағы
б) Екі тиын лақтырылған.
В
 ={екі елтаңба пайда болды} В
={екі елтаңба пайда болды} В
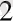 ={екі сан пайда болды}.
={екі сан пайда болды}.
в) Екі ойын кубы лақтырылған
С
 ={екі кубтада 6 цифры пайда болды}
={екі кубтада 6 цифры пайда болды}
С
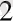 ={екі кубтада 6 цифры пайда болмады}
={екі кубтада 6 цифры пайда болмады}
C
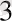 ={бір кубта 6 цифры болды, екінші кубта 6 цифры болмады}
={бір кубта 6 цифры болды, екінші кубта 6 цифры болмады}
5. Бір мезгілде 5 ойын кубы лақтырылсын. Сонда бір мезгілде 2 алты, 2 бес және 4 цифрлары жазылған жақтардың пайда болу ықтималдығы қандай?
6. 32 картадан 10 карта алынды. Осы 10 картаның ішінде 8 картаның бір түрлі болуының ықтималдығы қандай?
7. n бірдей шар салынған урнадан бір шар алынып қайта салыныды. Тәжірибе n рет қайталанғанда барлық шарлар түгел алынып шығуының ықтималдығы қандай?
8. Жеті перфокарта 1, 2, 3, 4, 5, 6, 7 цифрлар жазылған. Перфокарталар әбден қарастырылғаннанкейін кез-келген 4 перфокарта алынады да олар солдан оңға қарай қойылды. Сонда 5463 саны шығатындығының ықтималдығы қандай?
9. 36 картаның кез-келген 3 картасы алынады. Сонда тұз, король, дама шығуларының ықтималдығы қандай?
10. Группадағы 15 студентке, оның сегізі қыздар, театрға 8 билет берілді. Сонда театрға билет алған 8 студенттің екеуі қыздар болуының ықтималдығы қандай?
11. Ойын сүйегін лақтырғанда жүп сан шығуының ықтималдығы қандай?
12. Экспедициядағы 20 машинаның кез-келген 5 машинасы тексеруге алынды. Экспедицияда 2 машина істен шыққан болатын.
1. Алынған 5 машинаның барлығы да жарамды болуының ықтималдығы қандай?
2. Алынған 5 машинаның біреуі істен шыққан, ал төртеуінің жарамды болуының ықтималдығы қандай?
13. Әрбір 100 картаға 1-ден 100 дейін сан жазылған. Алынған кез-келген бір картада 5 цифріне еселі болатын сан шығуының ықтималдығы қандай?
14. Жәшіктегі 15 детальдың 10-ны боялған. Жинаушы кез-келген 3 деталь алды. Алынған 3 деталь де боялғандығының ықтималдығы қандай?
15. Бірінші жәшікте нөмірлері 1-ден 5-ке дейін, ал екіншісінде 6-дан 10-ға дейін шарлар бар. Әрбір жәшіктен бір-бірден шар алынды. Алынған екі шардың нөмірлерінің қосындысы болуының ықтималдығы қандай
16. Студент 60 сұрақтың 50-ін біледі. Әрбір билет екі сұрақтан тұрады. Алған билеттегі екі сұрақты да білетіндігінің ықтималдығы қандай?
17. Группадағы 30 оқушының бақылау жұмысында 6-ы “5”, 10-ы, “4”, ал 9-ы “3” деген бағалар алды. Тақтаға үш оқушы шақырылды. Шақырылған үш оқушының да “2” баға алғандығының ықтималдығы қандай?
18. Берілген кубтың барлық жақтары боялған. Куб бірдей 1000 бөлікке бөлінген. Пайда болған бөліктер, оларды кубтар, мұқият арастырылған, содан кейін бір кішкене куб алынған.
Алынған кішкене кубтың: а) бір жағы боялғандығының ықтималдығы қандай? б) екі жағы боялғандығының ықтималдығы қандай? в) үш жағы боялғандығының ықтималдығы қандай?
19. Белгілі бір 6 магазинді 3 ревизор тексеруі керек еді. Әр ревизор 2 магазинді тексеруі керек. Магазиндерге ревизорлар қалай болса солай бөлінеді. Сонда бірінші ревизордың кез-келген екі магазинге жіберілуінің ықтималдығы қандай?
20. 36 картаның кез-келген үшеуі алынды. Алынған үш картаның екеуі тұз болуының ықтималдығы қандай?
21. Қорапта нөмірленген бірдей 6 куб бар. Қораптан кез-келген ретпен барлық кубтар алынды. Алынған кубтар нөмірлерінің өсу ретімен шығуының ықтималдығын табу керек.
22. Партияда 10 детальдің 7-і сапалы. Алынған кез-келген 6 детальдің 4-і сапалы болуының ықтималдығын табу керек.
23. Екі ойын сүйегі лақтырылған. Екі сүйекте пайда болған сандардың айырмасының абсолют шамасы 2-ге тең болғандығының ықтималдығын табу керек.
24. Қораптағы бірдей 6 шар нөмірленген. Кез келген ретпен бір-бірлеп шарлар алынып бір қатарға солдан оңға қарай қойылған. Сонда алдын-ала ойланған бір сан шығатындығының ықтималдығын табу керек.
25. Орыс алфавитінің 32 әрпі әртүрлі карталарға жазылған. Содан кез келген 6 карта алынып бірінен соң бірі бір қатарға қойылған. Сонда “сурет” сөзінің пайда болуының ықтималдығын табу керек.
26. Урнада 5 ақ 3 қара шарлар бар. Кез келген екі шар алынды. Сонда алынған әр түсті болуының ықтималдығы қандай?
27. Винтовкадан 120 атыс жүргізілді. Сонда нысанаға тию жиілігі 0, 85-ке тең болды. Оқ қанша рет нысанаға дәл тиді?
28. Партиядағы 200 бұйымның бақылау кезінде 8 данасы сапасыз болды. Сапасыз бұйымдардың пайда болуының жиілігі қандай?
29. Ойын сүйегі лақтырылғанда 3-ке еселі болатын сан шығуының ықтималдығын табу керек?
2 Ықтималдақтарды қосу және көбейту теоремалары
Мысал 1 36 картаның ішінен кез-келген 2 карта алынсын. Осы екікартаның бір түсті болуының ықтималдығын табу керек.
Шешуі: Әуелі алынған екі картаның белгілі бір түске жататынының (айталық “қарға” болсын) ықтималдығын табалық. Белгілеу енгізелік. А-бірінші карта “қарға”болсын, В-екінші карта да “қарға” болсын. Бұл екі оқиға тәуелді оқиғалар, яғни В-ның пайда болу ықтималдығы А-ның пайда болуына, не пайда болмауына байланысты өзгеріп отырады. Сондықтан
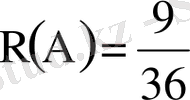 ,
,
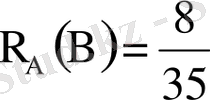
Осыдан
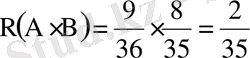
Ал енді
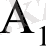 ,
,
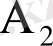 ,
,
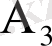 ,
,
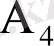 алынған екі карта сәйкес төрт түстің біріне жататындығын көрсететін өзара үйлесімсіз оқиғалар болсын. Сонда алынған екі картаның бірдей түсті (оқиға С) болуы
алынған екі карта сәйкес төрт түстің біріне жататындығын көрсететін өзара үйлесімсіз оқиғалар болсын. Сонда алынған екі картаның бірдей түсті (оқиға С) болуы
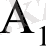 ,
,
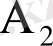 ,
,
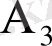 ,
,
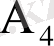 оқиғаларының кез-келгені орындалса пайда болады, яғни
оқиғаларының кез-келгені орындалса пайда болады, яғни
 С=
С=
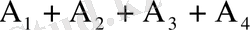 ;
;
Олай болса
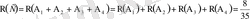
Мысал 2
Екі мерген атыс алаңында атыс жүргізуде. Бірінші мергеннің нысанаға тигізу ықтималдығы - 0, 7, екіншісінікі - 0, 8 тең. Егер екеуі де бір-бірден атыс жасаса, ең болмағанда біреуінің нысанаға дәл тигізетіндігінің ықтималдығы қандай?
Шешуі: Белгілеу енгізелік. А-бірінші мерген нысанаға дәл тигізді. В-екінші мерген нысанаға дәл тигізді. Бұл екі оқиға үйлесімді, себебі екі мерген де нысанаға дәл тигізуі мүмкін ғой. Сондықтан үйлесімді оқиғалардың қосындыларының ықтималдығы туралы теореманы пайдаланып:
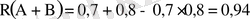
екенін табамыз.
Осы мысалды ең болмағанда бір оқиғаның пайда болуы (оқиға D) туралы теореманы пайдаланып та шығаруға болатынын көрсетелік. Шынында да D-оқиғасы ең болмаса біреуінің нысанаға тигізу болсын. Сонда
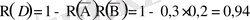
Бұл жерде
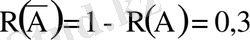 ,
,
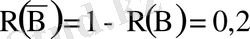 ,
,
Мысал 3
Екі жәшікке бөлшектер салынған. Бірінші жәшікте 10 бөлшек, оның үшеуі стандартты, екіншісінде -15 бөлшек онда 6 стандартты бар. Әрбір жәшіктен бір-бірден кез-келген бөлшек алынды. Алынған екі бөлшектіңде стандартты екенінің ықтималдығын табу керек.
Шешуі:
Белгілеу енгізелік. А-бірінші жәшіктен алынған бөлшек стандартты, В-екінші жәшіктен алынған бөлшек стандартты. Сондықтан
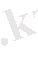
 /10,
/10,
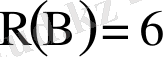 /15. Алынған екі бөлшекте стандартты болу үшін
/15. Алынған екі бөлшекте стандартты болу үшін
 оқиғасы пайда болуы керек. Бұл екі оқиғада үйлесімді, себебі екеуі бірдей пайда бола алады, сондай-ақ бұл оқиға тәуелсіз, себебі олардың пайда болуы бір-біріне байланыссыз. Сондықтан
оқиғасы пайда болуы керек. Бұл екі оқиғада үйлесімді, себебі екеуі бірдей пайда бола алады, сондай-ақ бұл оқиға тәуелсіз, себебі олардың пайда болуы бір-біріне байланыссыз. Сондықтан
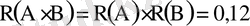
Мысал 4
Бөлшек дайындау процессі үш операциядан тұрады. Бірінші операция кезінде сапасыз бөлшек дайындалуының ықтималдығы - 0, 02, ал екінші операция кезінде -0, 03 және үшінші операция кезінде - 0, 02. Сапасыз бөлшектердің пайда болуын тәуелсіз оқиғалар деп қарастырып, осы үш операциядан кейін сапалы бөлшек дайындауының ықтималдығын табу керек.
Шешуі:
Белгілеу енгізелік. А оқиғасы деп бірінші операциядан кейін сапасыз бөлшектің пайда болуы; В - екінші операциядан кейін сапасыз бөлшек пайда; С - үшінші операциядан кейін сапасыз бөлшек пайда болуы. Есептің шарты бойынша А, В, С тәуелсіз оқиғалар. Олай болса
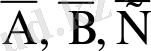 оқиғалары да тәуелсіз оқиғалар. Сондықтан
оқиғалары да тәуелсіз оқиғалар. Сондықтан
 D=
D=
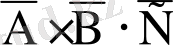 оқиғасы - үш операциядан кейін сапалы бөлшек дайындалуын анықтайды. Енді тәуелсіз оқиғалардың көбейтіндісінің ықтималдығының формуласын пайдаланып
оқиғасы - үш операциядан кейін сапалы бөлшек дайындалуын анықтайды. Енді тәуелсіз оқиғалардың көбейтіндісінің ықтималдығының формуласын пайдаланып
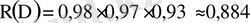
табамыз.
Мысал 5
Сүңгір қайықты іздеп табудың ықтималдығы 0, 8, ал оны жойып жіберудің ықтималдығы 0, 6 - ға тең. Іздеп табылған сүңгуір қайықты жойып жіберудің ықтималдығы қандай?
Шешуі: А - оқиғасы сүңгуір қайықты іздеп тауып алуды білдіреді. В - сүңгуір қайықты жқйып жіберуді білдіреді. Сонда
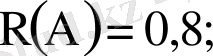
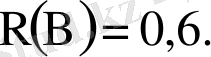
Есептің шарты бойынша іздеп табылған қайықты жойып жіберудің ықтималдығын табу керек, яғни
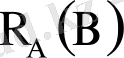 ықтималдығын табу керек.
ықтималдығын табу керек.
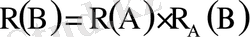
Сонда
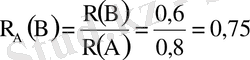
Мысал 6
Үш баскетболшы корзинаға бір-бірден доп лақтырды. Бірінші баскетболшының корзинаға доп түсіруінің ықтималдығы 0, 9, екіншісінікі -0, 8,
үшіншісінікі - 0, 7. Тек бір баскетболшының корзинаға доп түсіруінің ықтималдығы қандай?
Шешуі:
А - бірінші баскетболшының корзинаға доп түсіруі, В, С - екінші, үшінші баскетболшының корзинаға доп түсіруі. Бұл оқиғалар тәуелсіз. Енді мына оқиғаларды қарастырайық:
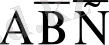 -тек А-оқиғасының пайда болуы,
-тек А-оқиғасының пайда болуы,
 -тек В оқиғасының пайда болуы,
-тек В оқиғасының пайда болуы,
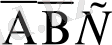 - тек С оқиғасының пайда болуы.
- тек С оқиғасының пайда болуы.
Бұл соңғы үш оқиғалар үйлесімсіз сондықтан
D=
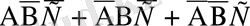
оқиғасы А, В, С оқиғаларының тек біреуінің пайда болуын білдіреді. Сөитіп
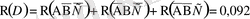
Мысал 7
Үш аңшы ұшып бара жатқан қазды сәйкес 2/3, ¾, ¼ ықтималдықтарымен атып түсіре алады. Ұшып бара жатқан қазды үшеуі де бір мезгілде атты. Қазды атып түсіргендіктің ықтималдығы қандай?
Шешуі: Қазды атып түсіру үшін ең болмағанда бір аңшының оғы дәл тиюі керек. Сондықтан мына формуланы пайдаланып
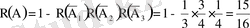
табамыз.
Мұндағы
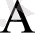 - қаз атып түсірілді;
- қаз атып түсірілді;
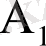 - қазды бірінші аңшы атып түсірді;
- қазды бірінші аңшы атып түсірді;
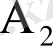 - қазды екінші аңшы атып түсірді;
- қазды екінші аңшы атып түсірді;
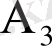 - қазды үшінші аңшы атып түсірді;
- қазды үшінші аңшы атып түсірді;
Мысал 8
Екі қорапқа ақ және қара түсті бірдей шарлар салынған. Айталық бірінші қорапта m
 ақ, n
ақ, n
 қара, ал екіншісінде - m
қара, ал екіншісінде - m
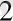 ақ, n
ақ, n
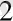 қара шарлар бар болсын. Екі қораптан бір мезгілде, бір-бірден кез-келген шарлар алынған. Алынған екі шардың ең болмағанда біреуі ақ шар болғандығының ықтималдығын табыңыз.
қара шарлар бар болсын. Екі қораптан бір мезгілде, бір-бірден кез-келген шарлар алынған. Алынған екі шардың ең болмағанда біреуі ақ шар болғандығының ықтималдығын табыңыз.
Шешуі: А- оқиғасы бірінші қораптан ақ шар алынғандығын білдірсін, В- екінші қораптан ақ шар алынғандығын білдірсін. Сонда А+В оқиғасы алынған екі шардың ең болмағанда біреуі ақ шар болғандығын білдіреді. Бұл екі оқиға үйлесімді. Сондықтан мына формуланы пайдаланымыз.
Бұл жерде
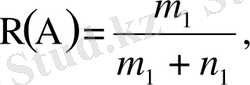
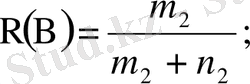
және А және В оқиғаларының тәуелсіздігін ескеріп
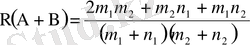
табамыз.
Мысал 9
Қорапта бірдей бұйым бар. Қораптан екі сапалы бұйым алудың ықтималдығы 4/15 тең. Қорапта қанша сапалы бұйым бар еді?
Шешуі:
Белгілеу енгізелік. А- қорап бірінші рет алғанда сапалы бұйым алынды, В- қорапта екінші рет алғанда сапалы бұйым алынды. Бұл екі оқиғалар тәуелді. Сондықтан, егер
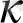 - сапалы бұйымдар сан десек онда
- сапалы бұйымдар сан десек онда
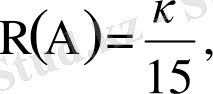
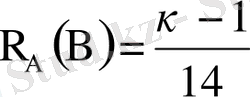
Есептің шарты бойынша
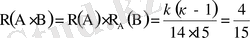
Осыдан
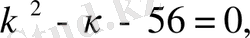
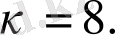
Сонымен жәшікте 8 сапалы бұйым болды.
Студенттерге өзіндік есептер1 Тоқ кернеуі ұлғайтылғанда бір-бірімен тізбектес жалғанған үш элементтің бірінің істен шығуына байланысты электр жүйесінде үзіліс пайда болуы мүмкін. Элементтердің істен шығуларының ықтималдықтары сәйкес 0, 2; 0, 3; 0, 4. Электр жүйесінде үзіліс болмауының ықтималдығын табу керек.
Нұсқау: Электр жүйесінде үзіліс болмау үшін ешбір элемент істен шықпауы керек.
2 Бір партияда 50 зат бар, оның 5-уі сапасыз. Осы партиядан алынған кез-келген 30 заттың ішінде сапасыз зат біреуденартық болмауының ықтималдығын табу керек.
Нұсқау: Белгілеу енгізейік. А- барлық 30 зат сапалы. В- 30 заттың біреуі сапасыз. Сонда А, В оқиғалары үйлесімсіз. Олай болса С=А+В - алынған 30 заттың ішінде сапасыз зат біреуден артық еместігін білдіретін оқиға.
3 Жәшіктегі10 детальдің 4-і боялған. Деталь жинаушы 3 деталь алды.
Алынған үш детальдің ең болмағанда біреуі боялғандығының ықтималдығын табу керек.
4 Ақшалай-заттай лотереяда әрбір 1 билетке 150 заттай және 50 ақшадайұтыс шығады. Бір билеті бар адамға не заттай, не ақшалай ұтыс шығуының ықтималдығы қандай?
5 Урнада он қызыл, 5 көк және 15 ақ шарлар бар. Түсті шардың алынуының ықтималдығы қандай?
6 Лотереяда 1000 билет бар. Оның әрбір екі билетінің біріне ұтыс шығады. Екі билет сатып алынған. Осы екі билетке де ұтыс шығуының ықтималдығы қандай?
7 Екі ойын сүйегі лақтырылған. Сонда пайда болған сандардың қосындысы 5-тен артық болмауының ықтималдығын табу керек.
8 Үш ойын сүйегі лақтырылған. Сонда үш сүйекте де бірдей сан пайда болуының ықтималдығы қандай?
9 Екі күміс теңгені лақтырғанда ең болмағанда бір рет “цифр” пайда болуының ықтималдығы қандай?
10 Урнада 9 қызыл, 6 көк шарлар бар. Кез-келген екі шар алынды. Алынған екі шардың да қызыл болуының ықтималдығын табу керек.
11 Жұмысшы үш станоктің істен шықпауын қамтамасыз етеді. Бір сағат ішінде жұмысшының қадағалауынсыз жұмыс істеу ықтималдығы бірінші станок үшін 0, 3-ке тең, екіншісі үшін - 0, 5 және үшіншісі 0, 6. Мына оқиғалардың ықтималдығын табу керек:
а) Бір сағат бойында ең болмағанда бір станок жұмысшының қадағалауынсыз жұмыс істейді;
в) Екі сағат бойы үш станок те жұмысшының қадағалауынсыз жұмыс істейді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz