Жылуөткізгіштік теңдеуінің анық айырымдық схемасы, оны шешудің сандық тәсілі

Пән: Автоматтандыру, Техника
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 85 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министірлігі

Абай атындағы Қазақ Ұлттық Педагогикалық Университеті

Физика - математика факультеті

Теориялық физика жене сандық модельдеу кафедрасы

Курстық жұмыс

Тақырыбы: «Жылуөткізгіштік теңдеуінің анық айырымдық схемасы, оны шешудің сандық тәсілі»

Қорғауға жіберілді.

«»2007 жыл.

Теориялық физика жене сандық модельдеу

кафедрасының меңгерушісі

профессор, фил-мат. ғ. д. Косов В. Н.

Ғылыми жетекшісі: профессор Құлбек М. Қ.

Орындаған: 6А0604 «Физика» мамандығының,

қазақ бөлімінің магистаранты Мәлік Т. З.

Алматы 2007

МАЗМҰНЫ

Кіріспе

І. Тарау Жылуөткізгіштік теңдеуі туралы жалпы түсінік

1. 1 Жылуөткізгіштік теңдеуі

1. 2 Жылуөткізгіштікке арналған қарапайым стационарлық тапсырмалар

1. 3 Стационарлы емес тапсырмалар. Жалғыздық теоремасы

ІІ. Тарау Стационарлық емес жағдайдағы жылу өткізгіштік теңдеуінің анық айырымдық схемасы және оны шешудің сандық әдістері

2. 1 Айырымдық схема теориясының элементтері

2. 2 Айырымдық схеманы құру

2. 3 Дифференциалды жылу өткізгіштік теңдеуінің анық айырымдық

схемасы

2. 4 Стационар емес жағдайдағы жылу өткізгіштік теңдеуін шешудің

сандық әдістері

Қорытынды

Компьютерлік бағдарлама және оның тәжірибелік нәтижелері

Пайдаланылған әдебиеттер

Кіріспе

Табиғатта, техникада және технологияда жылуөткізгіштік процестері өте күрделі жағдайларда жүреді. Біріншіден, олар стационарлы емес режимдерде өтеді. Екіншіден, материалдарды (мысалы, табиғи шикізаттарды, минералдарды, т. б) қыздыру барысында әртүрлі температуралар аймағында табиғаттары сан алуан фазалық және химиялық түрленулер орын алады. Бұл өзгерістер көбіне жылу эффектілерімен (эндотермиялық және экзотермиялық) байланысты жүріп, үлгінің бойында зат массасының тасымалдануына және құрылымдық өзгерістерге (деформацияға) әкеп соғады. Бұл процестер өз ретінде жылуөткізгіштік құбылысының бұрынғыдан да күрделене түсуіне әкеледі. Мысалы, табиғи шикізаттардан жасалынатын кирамикалық материалдар техналогиясында осындай күрделі физикалық, химиялық процестер мен тасымалдау құбылыстары орын алады.

Бұл курстық жұмыста жалпы жылуөткізгіштік және жылуөткізгіштік теңдеуінің анық айырымдық схемасы, оны шешідің сандық тәсілі қарастырылады. Есептеуіш машиналарды кең көлемді пайдалана отырып, жылдам әрі тиімді нәтижелерге қол жеткізу үшін сандық әдістерге көбірек көңіл бөлінген.

Курстық жұмысымның мақсаты стационарлық емес жағдайдағы жылу өткізгіштік процесін зерттеп, температуралық өрістерді алу болды. Сондықтан зерттеу нысаны ретінде керамикалық материал жазық үлгі пішінінде алынды. Есептің Turbo Pascal программалау тілінде компьютерлік бағдарламасы құрылып, нәтижесінде алынған мәндер бойынша температуралық өрістер салынады. Есептеу тәжірибелерінің нәтижесінде алынған температуралық өрістер геометрилық өлшемдері әр түрлі жазық керамикалық үлгілерді әр түрлі жылдамдықтармен қыздыру барысындағы жылуөткізгіштік процестерінің динамикасын анықтауға мүмкіндіктер береді.

І. Тарау Жылуөткізгіштік теңдеуі туралы жалпы түсінік

1. 1 Жылу өткізгіштік теңдеуі

1. ХІХ ғасырдың алғашқы жылдарында (1768-1830) француз математигі Фурье жылуөткізгіштіктің математикалық теориясының негізін қалады. Әрине ол кездегі көзқарас пен қазіргі кездегі тұжырымдардың арасында елеулі келіспеушіліктер мен айырмашылықтар көп болды. Сонан соң, жылу берілу міндетті түрде жылу алмасу процесі негізінде жүретіндігі ұсынылды. Конвекция жоқ деп қарастырылды. Қатты денелерде бұл мүмкін еді. Ал сұйықтар мен газдарда конвекцияны болдырмау үшін, мысалға алғанда, бұл денелерді үстінен (жоғарыдан ) қыздырды. Сонымен бірге, жүйенің көлемін тұрақты деп қарастырды, сондықтан жылу берілу процесі кезінде ешқандай зат алмасу жүрмейді.

2. Жылуөткізгіштіктің математикалық теориясында жылудың таралуы сұйық ағысы ретінде қарастырылады. Жылу ағынының бағытына перпендикуляр 1см ² жазықтықты 1с ішінде жүріп өтетін жылу мөлшерінің сан мәніне тең және бағыты жағынан жылудың таралу бағытымен бағыттас болатын j векторын жылу ағынының тығыздығы деп атайды.

Енді бір өлшемді есептердегі j векторын қанағаттандыратын дифференциалдық теңддеуді табайық.

х осіне параллель бағытта өтетін жылу ағыны туындайтын шектеусіз орта болсын делік. Бір өлшемді жалпы жағдайда жылу ағынын сипаттайтын ортаның құрылымы мен биіктігі осы бағытта өзгере алады. Сонымен қатар, олар уақыт бойынша да өзгеріске ұшырайды. Сондықтан, жылу ағынының тығыздығын j - x координатасы мен уақыт t:j=j(x, t) функциялары ретінде қарастыру керек. Ойша (1. 1-сурет)

Ортада шексіз ұзын призма немесе х осіне параллель цилиндрді ерекшелеп алып, осындай АВ цилиндірінің шексіз аз бөлігін dx қарастырамыз. S - цилиндр бетінің қиылысу ауданы болсын. АВ цилиндіріне А мен х координатасы аралығына dt уақытында берілетін жылу мөлшері j(x) Sdt тең. Сол уақыттағы В - дан өтетін жылу мөлшері j(x+dx) Sdt . Цилиндрдің бүйір бетінен жылу берілмейтіндіктен цилиндірдің қарастырылып отырған бөлігінен dt уақыт мезетінде берілетін толық жылу мөлшері:

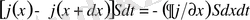
Бірақ, осы жылуды мына түрде беруге болады 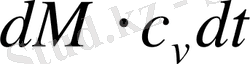, мұндағы 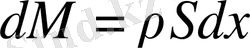- АВ цилиндірінің массасы, 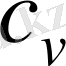- жылу сыйымдылығы, dt - температураның көтерілуі. Екі белгіленуді теңестіре және қарастыра отырып алатынымыз

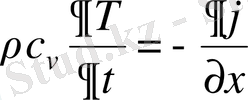(1. 1)

3. Енді жылу ағынының тығыздығы мен ортаның температурасы Т арасындағы байланысты енгізу керек. Орта температурасы нүктеден нүктеге өзгергенде ғана жылу ағыны орын алатындығын тәжірибе көрсетті. Жылу әрқашан жоғарғы температурадан төменгі температураға қарай өтеді. Ең қарапайым жағдай 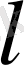қалыңдықты шексіз біртектіпластинка. Егер, пластинканың бір жазық шекарасында температура Т ₁ , ал екіншісінде температура Т ₂ , әрине 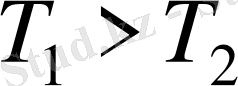болса, онда тәжірибе көрсеткендей жылу ағыны температуралар айырымына пропорционал және пластинканың қалыңдығына 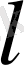кері пропорционал болады. Математикалық тұрғыдан бұны мына түрде көрсетеміз:

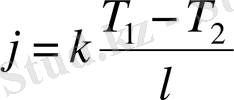(1. 2)

мұндағы 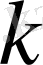- тек қана пластинканың материалы және оның физикалық жағдайына тәуелді оң мәнде тұрақтылығының жылуөткізгіштігі деп аталады.

Пластинканы шексіз жіңішке деп алайық. Егер х осі температураның төменгі бағытына қарай бағытталса, онда

, , ,

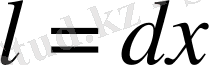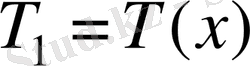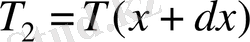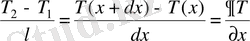(1. 1) формуласы мына түрге ие болады:

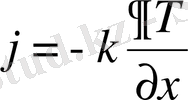(1. 3)

(1. 3) белгіленуі х осінің бағыты температураның өсуіне қарай бағытталса да дұрыс болып қала береді, өйткені бұл жағдайда

, , ,

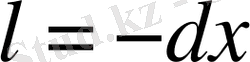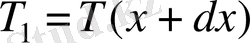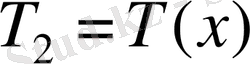сонымен бірге ол біртекті есмес ортаның жалпы жағдайында және тек қабатты орта емес, құрылымы мен температурасы барлық үш x, y, z кеңістік координаталарының функциясы болатын ортада да дұрыс болып табылады.

Жылуөткізгіштік 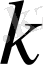барлық үш x, y, z кеңістік координаталарының функциясы. Біздің бір өлшемді есебімізде ол тек бір ғана кеңістік координаталарына х тәуелді болады: .

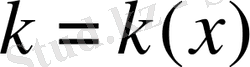(1. 3) белгіленуін (1. 1) формуласына қойсақ,

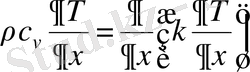(1. 4)

Бұл теңдеу жылуөткізгіштік теңдеуі деп аталады. Жеке жағдайда, орта біртекті болғанда, 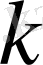жылуөткізгіштік температураға тәуелді болмайды, онда теңдеу мына түрге ие болады.

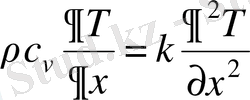(1. 5)

немесе

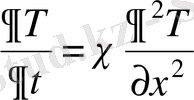(1. 6)

мұндағы 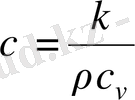(1. 7)

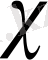- тұрақтысы ортаның температура өткізгіштігі деп аталады.

Ортада жылу көздері болуы мүмкін. Мысалға, радиоактивті ыдырау немесе электор тогының өтуі нәтижесінде жылу бөлінуі мүмкін. Бұндай жылу көздерін біз ескермедік. Оларды ескеру үшін, 1 м ³ орта көлемінде 1с уақыт аралығында жылу көздерінен бөлінетін жылу мөлшеріне тең q шамасын енгіземіз. Сонда (1) теңдеуі былайша жазамыз:

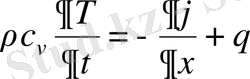(1. 8)

Осыған сәйкес қалған теңдеулер де өзгеріске ұшырайды.

4. Ортаның құрылымы мен температурасы барлық үш x, y, z кеңістік координаталарына тәуелді болатын жалпы жағдайда дененің жылу балансын бейнелейтін жылуөткізгіштік теңдеуі :

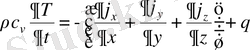
(1. 9)

Бірақ, бұндай теңдеулердің шешімдерін аналогиялық түрде тек қана қарапайым жағдайларда алуға болады. Орта мен ондағы температураның таралуы сфералық немесе цилиндірлік симметриялы болған жағдай ең маңызды болып табылады. Сондықтан, біз (1. 9) теңдеуін шешпей-ақ сфералық және цилиндірлік симметрия жағдайымен шектелеміз. Бұл жағдайларда тікбұрышты жүйе координаталарының орнына сфералық және цилиндірлік координаталар жүйесін қолданған тиімді.

Бірінші сфералық симметрия жағдайын қарастырамыз. Уақытпен бірге тек қана r-ге тәуелді болатын жылу ағыны тығыздығының векторы j радиус бойымен бағытталған. Симметрия центірінің айналасына r және r + dr радиустарымен бірге екі концентрациялық сфераларды жазамыз (1. 2-сурет) . dt уақыт мезетінде осы екі сфераның аралығындағы кеңістікке олардың бірі арқылы келіп түсетін жылу мөлшері: 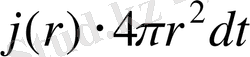. Сол уақыт мезетінде екінші сфера арқылы өтетін жылу мөлшері: 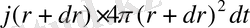. Мәселе аргументтің әр түрлі мәндеріндегі r және r + dr сол бір ғана jr ² функция жөнінде екендігін ескеру үшін осы екі жылу мөлшерін мына түрде жазған ыңғайлы:

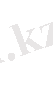
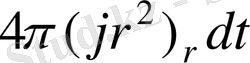
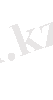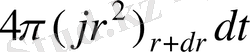
және 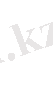. Олардың арасындағы айырмашылық

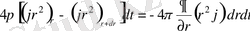
қоршаған кеңістіктегі қарастырылып отырған

сфералық қабаттан dt уақыт мезетінде өтетін жылу мөлшерін береді. Жылу көздері бар кезде одан түскен 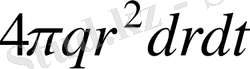жылу мөлшерін қосу керек. Бірақ қабаттағы жылу мөлшерінің өзгерісін мына түрде беруге болады: 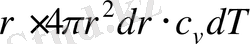. Сондықтан, жылу балансының теңдеуі

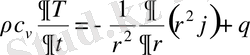(1. 10)

(1. 3) қатынасының орнына 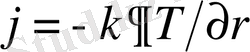, ендеше

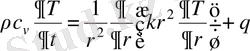(1. 11)

Цилиндірлік симметрия жағдайында да аналогиялық талқылаулар жүргізіледі. r - ді симметрия осіне дейінгі қашықтық деп есептеп, алатынымыз

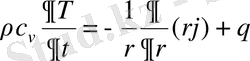(1. 12)

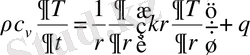(1. 13)

5. Екі еркін орта бөліктерінің шекарасында орындалуы тиіс жалпы қатынастарды жылуөткізгіштік теңдеуіне қосу қажет. (1. 3-сурет)

Шекаралық шарт: Белгіленген шекараның екі жақ беті де бірдей нормаль құраушы векторлар болуы тиіс. Шынымен де, АВ - орта бөлігінің шекарасы болсын, ал n- нормальдың бірлік векторы, мысалға бірінші ортадан екіншіге үргізілген. Бөлік шекарасына перпендикуляр және одан әр түрлі бағытта негізделген құрылымды шексіз аз цилиндрді ойша жүргіземіз. Цилиндрдің биіктігі h негіздің сызықтық өлшемдерімен салыстырғанда жоғары ретті шексіз аз болу керек. Сонда, цилиндрдің бүйір беті арқылы өтетін жылу ағынынан қорғауға болады. Егер S- цилиндр негізінің ауданы болса, онда 1с ішінде оған түсетін жылу мөлшері мынаған тең:

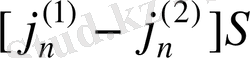
Бірақ, бұл өлшем цилиндірдегі жылу мөлшері сияқты оның көлеміне Sh пропорционал болуы тиіс, яғни 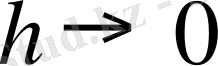шегінде нольге айналуы қажет. Сондықтан, шекте, АВ шекарасында цилиндрдің екі негізі бір-бірімен біріккенде,

(1. 14)

Болуы керек. Демек, кез келген шекарада жылу ағыны векторының нормаль құраушысы үздіксіз болады. Бұл дәлелдеме, бөлік шекарасында шекті беттік тығыздықты жылу көздері жоқ екендігін жорамалдайды.

1. 2 Жылуөткізгіштікке арналған қарапайым стационарлық тапсырмалар .

Жылуөткізгіштікке арналған барлық тапсырмалар стационарлық және стационарлық емес болып бөлінеді. Уақыт өтуіне қатысты температура Т өзгермесе тапсырмалар стационарлық деп аталады. Ол тек кеңістік кординаталарының функциясы болып табылады. Бұл жағдайда 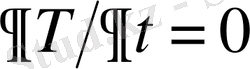. Бірмәнді есептерде Т тек бір ғана кеңістік координатасына тәуелді болады, демек белгіде дербес туындылар қажет емес. Қарапайым стационарлық бірмәнді есептерді қарастырайық.

1. Шексіз жазық параллель пластинкадағы температураның стационарлық таралуы.

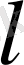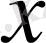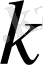
Айталық, беті тұрақты Т ₁ және Т ₂ температураларымен ұсталған, қалыңдығы шексіз пластинка болсын. Осындай пластинканың ішіндегі Т температураның таралуын анықтау керек. Пластинкаға перпендикуляр түзуді осі деп есептейміз. Пластинканы шектейтін 1 жазықтыққа координаталар басын орналастырамыз. Жылуөткізгіштік 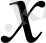координатасына тәуелді болуы мүмкін. (1. 4) теңдеуі былай түрленеді:

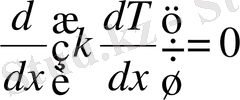
Бұдан, 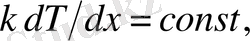немесе (3), 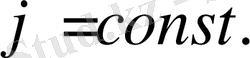Жылу ағыны тығыздығының тұрақтылығы пластинканың біртекті немесе біртекті емес екендігіне тәуелсіз. Енді, біртекті пластинканың қарапайым жағдайын қарастырамыз. Бұл жағдайда 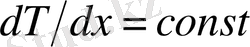болғандықтан 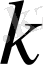жылуөткізгіштік тұрақты болады. Тұрақтыны 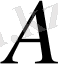әріпімен белгілеп және интегралдай отырып, алатынымыз

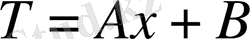
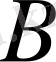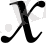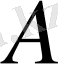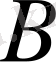мұндағы, - екінші интегралдау тұрақтысы. Пластинкаға кесе температура координатасымен сызықтық заң бойынша өзгереді. және тұрақтылары жылуөткізгіштікке мүлде тәуелсіз. Олар шекаралық шарттан анықталады. болғанда, , ал 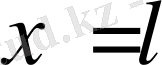болғанда 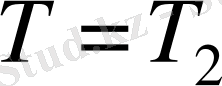. Бұдан мына теңдеулер жүйесіне келеміз:

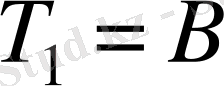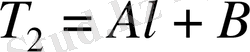
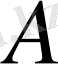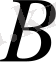Одан және тұрақтыларын анықтай отырып, температураның таралуын табамыз:

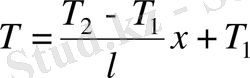(1. 15)

2. Екі концентрациялық сфералар аралығындағы температураның температураның стационарлық таралуы.

Ішкі сфераның радиусын 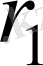, ал сыртқы сфераның радиусын 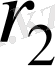деп белгілейміз. Сфералар арасындағы кеңістік жылуөткізгіштігі 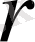- ге тәуелді болатындай ортамен толтырылған. (1. 11) сәйкес, ортада жылу көздері болмаса температураның таралуы мына теңдеу арқылы жазылады:

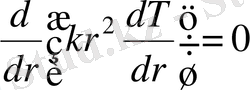
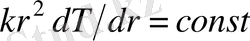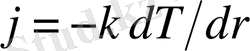
Ол береді. Сонымен, жылу ағынының тығыздығы 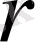арақашықтықтың квадратына кері пропорционал өзгереді. Сондай болуы қажет те, себебі 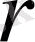сфера радиусы арқылы өтетін жылу ағыны 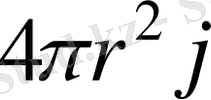тең, ал бұл ағын барлық сфераға бірдей болуы керек. Енді, айталық, сфералар аралығындағы орта біртекті болсын. Сонда, 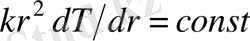болғандықтан, 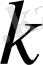жылуөткізгіштігі тұрақты болады. Тұрақтыны 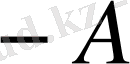белгілеп, алатынымыз 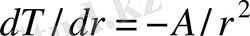, немесе интегралдағаннан кейін

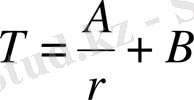
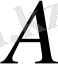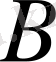және интегралдау тұрақтылары сфералық қабат шекарасындағы температурасы қабылдайтын мәннен анықталады. Бұл мына теңдеулер жүйесіне әкеледі:

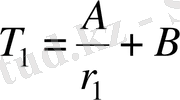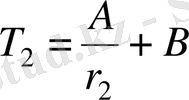
Одан 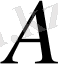және тұрақтыларын анықтау арқылы, сфералар аралығындағы температуралар таралуын табамыз:

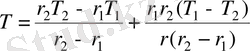(1. 16)

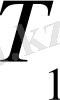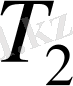3. Екі концентрациялық шексіз ұзын цилиндрлер аралығындағы температураның стационарлық таралуы. Ішкі цилиндр радиусын , ал сыртқы цилиндрлер радиусын деп белгілейміз. Олардың температуралары және тұрақты мәндерінде ұсталады. Цилиндрлер аралығындағы температураның стационарлық таралуы алдыңғы жағдайлардағыдай болады. Егер, цилиндрлер аралығындағы орта біртекті болса,

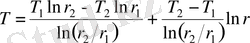(1. 17)

болады.

1. 3 Стационарлы емес тапсырмалар. Жалғыздық теоремасы.

1. Жылу таралатын орта біртекті , яғни ортаның барлық параметрлері координатаға тәуелсіз болсын деп есептейік. Сонымен қатар, олар уақыт пен температураға тәуелсіз, яғни тұрақты болсын делік. Егер, температурасы тек бір ғана 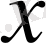кеңістік координатасы мен уақытқа тәуелді болса, жылу көздері бар кезде жылуөткізгіштік теңдеуі (1. 8) немесе (1. 3) ескерсек:

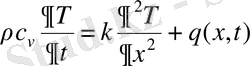(1. 18)

болады. жылу көздері “қуатының тығыздығы” берілген функциясының координатасы мен уақыты деп есептелуі керек. Бірақ, (1. 18) теңдеуінің көздерін шешу тапсырмалары әлі бірмәнді анықталмайды. Күнделікті бастапқы және шекаралық шарттар келесілерден құралады. Бастапқы шарттар бастапқы санақ уақыты ретінде қабылдауға тиімді болатын уақыттың қандай да бір моментінде бүкіл дененің температурасын анықтайды.

Бұл шартты мына түрде жазуға болады:

(1. 19)

мұндағы 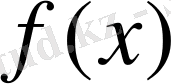- 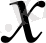координатаның берілген функциясы. Шекаралық шарттар уақыттың барлық моментінде дене шекарасындағы дене температурасын анықтайды. Бірмәнді жағдайларда, және 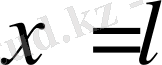жазықтықтарымен шектелген дене жазықпараллель пластинка түріне ие болады. Сондықтан шекаралық шарттар мына түрде жазылады:

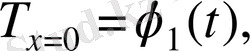
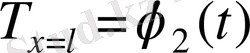(1. 20)

мұндағы, 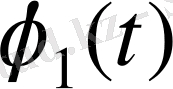және 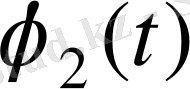- берілген уақыт функциялары.

2. Біріктірілген шеткі тапсырманың жалғыздық шешімі былай түсіндіріледі, яғни - қалыпты орынды шама болып табылады.

Шешімнің жалғыздығын дәлелдеу үшін, (1. 18) теңдеуі (1. 19) бастапқы және (1. 20) шеттік шарттарды қанағаттандыратын 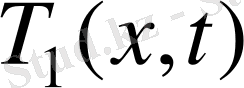және 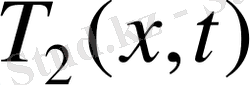екі шешімге ие болады деп есептейміз. Сонда,

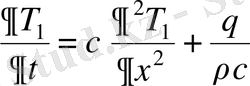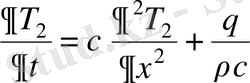
Көлемді есептеу және белгіленуін жаза отырып,

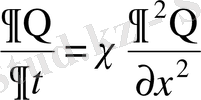(1. 21)

аламыз, яғни 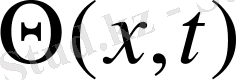функциясы жылу көздерінсіз жылуөткізгіштік теңдеулерін қанағаттандырады. Сонымен қатар, бұл функция “нольдік” бастапқы және шекаралық шартты белгілі:

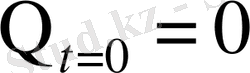кез келген 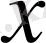; (1. 22)

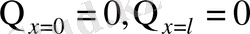кез келген . (1. 23)

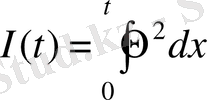интегралын қарастырайық. Бұл теріс болмайтындығы түсінікті. Сонымен бірге (1. 22) ескерсек, 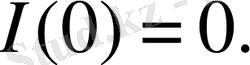Уақыт бойынша 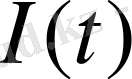туындысының интегралын табамыз:

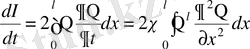
Бөліктеу интегралдау арқылы алатынымыз:

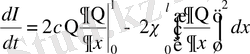
Оң бөліктің бірінші қосындысы (1. 23) шекаралық шарттың нольдік түріне айналады. Екінші қосынды теріс немесе ноль, өйткені 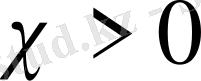. Сол себепті, 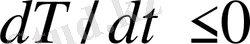. Уақыт өтуіне байланысты интеграл тек жойылуы немесе тұрақты болып қалуы мүмкін. Біріншісі мүмкін емес, себебі 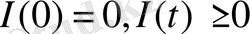болуы тиіс. Жалғыз қалатын мүмкіндік , яғни 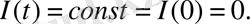Бұл тек 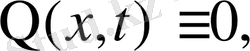яғни 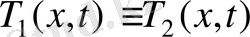болғанда ғана мүмкін. Шешімнің жалғыздығы дәлелденді. Талқылай отырып, жалғыздық теоремасының сфералық немесе цилиндірлік симметриялы тапсырмаларға да орынды екендігін оңай көрсетуге болады. Бұл барлық үш кеңістік координатасына тәуелді болғандағы көлденең формалы денеге де орынды болып қалады. Дәлелдеу дәл осылайша жүргізіледі, тек жәй интегралдың орнына көлемді және беттік интегралдарды қолдану керек. Егер, қандай да бір әдіспен, бастапқы және шекаралық шарттарды қанағаттандыратын жылуөткізгіштік теңдеуінің шешімін табу мүмкін болса, онда, жалғыздық теоремасы тапсырманың ізделініп отырған шешімі болып табылады.

3 . Сонымен қатар, шешімнің жалғыздығы басқа да себептерге байланысты шартталған есептер болуы мүмкін. Мысал ретінде келесі есепті қарастырамыз.

Әр түрлі температуралы 1 және 2 жылудан оқшауланған екі дене дәл сондай бүйір беті жылудан оқшауланған біртекті жылу өткізетін стерженмен жалғанған. Дененің бастапқы температурасы сәйкесінше, және . Осы денелердің уақыт бойынша температура өзгерісінің заңын табу керек.

Анықталмағандықтың таралуы үшін ең бірінші екі дененің де жылуөткізгіштігі өте жоғары (математикалық - шексіз үлкен) деп есептейміз. Сонда дененің әр түрлі бөліктері температураларының теңесуі тез жүреді. Сондықтан, t уақыттың әрбір моментінде 1 және 2 денені түгелдей дерлік сипаттайтын белгілі 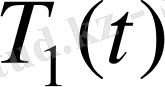және 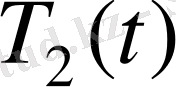температураларды енгізу қажет. Бірақ, тапсырманың түгелдей анықталуы үшін бұл жеткіліксіз. Сондықтан стерженге қатысты кейбір қосымша болжамдар енгіземіз. Стерженнің көлденең қимасы арқылы өтетін жылу ағыны ондағы температураның бастапқы таралуына тәуелді болады. Егер, стерженнің бастапқы температурасы тең болса, 1-ші денемен шекарада стерженде бастапқы уақыт моментінде ешқандай жылу ағыны жүрмейді, бірақ дәл сол кезде 2-ші денемен шекарада ағын максимал болады. Егер стержен және аралығында аралық температураны иеленсе, бастапқы жылу ағыны қимадан қимаға стержен бойымен өткенде өзгеріп отырады. Дегенмен, стерженнің жылу сыйымдылығы 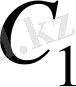және денелермен салыстырғанда жеткілікті аз. Біраз уақыт өткен соң стерженде температураның біркелкі төмендеуі байқалады, ондағы стержен бойындағы жылу ағыны өзгермейді. Осы уақытта сыйымдылығы жоғары 1 және 2 денелердің температурасы өзгермейді. Сондықтан да жылу ағынының қондырылу процесін ескермейміз, себебі о бастан стержен бойындағы жылу ағыны оның барлық қималарында бірдей болады. Сонда тапсырма матиматикалық анықталған болады, яғни бірмәнді. Анықтылық үшін 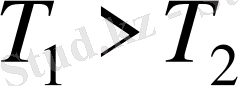делік. 1 денеден 2 денеге стержен бойымен өтетін жылу ағыны :

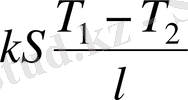мұндағы, 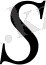стерженнің көлденең қимасының ауданы, 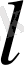- оның ұзындығы. Бұл ағын сан мәні бойынша 1 денедегі жылу жылдамдығының кемуіне немесе 2 денедегі жылу жылдамдығының өсуіне тең. 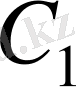және жылу сыйымдылықтарын тұрақты деп, 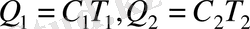жазуға болады. Бұдан шығатын теңдеу:

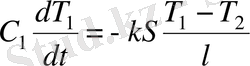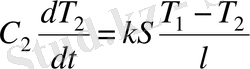, (1. 24)

(1. 24) бөлігінің қосындысы

+ ,

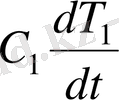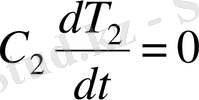
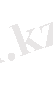немесе интегралдағаннан соң 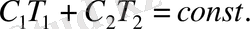Бұл теңдеу 1 және 2 денелердегі толық жылу мөлшерінің сақталуын білдіреді. Бастапқа кезде 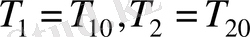, өйткені

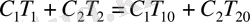(1. 25)

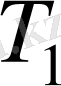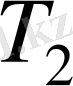және белгісіздерін анықтау үшін бұл теңдеу жеткіліксіз. Бұл жеткіліксіз теңдеуді табу үшін 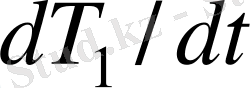және 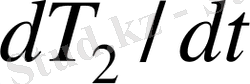туындыларына қатысты (1. 24) теңдеуін шешеміз және бірінші теңдеуден екіншісін мүшелеп есептейміз. Сонда алатынымыз

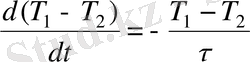(1. 26)

мұндағы,

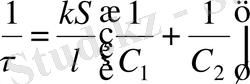(1. 27)

тұрақты уақыт өлшемдеріне ие. (1. 26) теңдеуді интегралдай отырып, алатынымыз

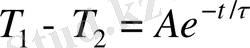
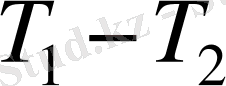температуралар айырымы уақытқа байланысты экспоненциальды заң бойынша азаяды. уақыт мезетінде бұл айырма рет азаяды. Сол үшін 1 және 2 денелер арасындағы жылулық тепе-теңдіктің тұрақталу уақытын білдіреді. Ол қарастырылып отырған денелердің релаксация уақыты немесе температуралардың теңгерілу уақыты деп аталады. Интегралдау тұрақтысы 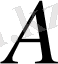бастапқаы шарттардан табылады: 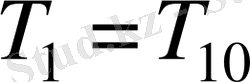, 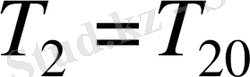егер, . Бұл

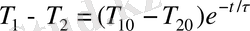(1. 28)

Енді (1. 25) және (1. 28) теңдеулер жүйесін есептей отырып алатынымыз

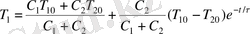
(1. 29)

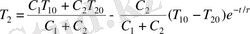
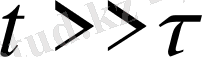болса, бұл теңдеулердің экспоненциальдық мүшілері елеусіз аз, және (1. 29) формуласы “қосынды температурасы” анықтайтын жалпыға белгілі теңдеуге өтеді.

ІІ. Тарау Стационарлық емес жағдайдағы жылу өткізгіштік теңдеуінің анық айырымдық схемасы және оны шешудің сандық әдістері.

2. 1 Айырымдық схема теориясының элементтері.

Қарапайым дифференциалдық теңдеулердің шешімі тек бір ғана айнымалыға тәуелді: 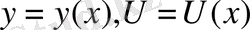және т. с. с. көптеген практикалық есептерде бастапқы функциялар бірнеше айнымалыларға тәуелді болады және осындай есептерді сипаттайтын теңдеулер бастапқы функцияның дербес туындыларынан тұруы мүмкін. Мұндай теңдеулер дербес туындылы теңдеулер деп аталады.

Дербес туындылы теңдеулердің шешіміне мысалға тұтас орта механикасының көптеген есептерін келтіреді. Мұнда бастапқы функция қызметін әдетте, аргументтерді қарастырып жатқан кеңістік нүктелерінің координатасы уақыт болып табылатын: тығыздық, температура, кернеу және т. б. атқарады. Есептің толық математикалық қойылуы дифференциалдық теңдеулермен қатар, сондай - ақ кейбір қосымша шарттардан тұрады. Егер шешім белгілі бір шектелген облыста ізделсе, онда оның шекарасына шектік шарттар деп аталатын шарттар қойылады. Мұндай есептер дербес туындылы теңдеулерге арналған шектік есептер деп аталады.

Егер қарастырып жатқан есепте тәуелсіз айнымалылардың бірі - уақыт болып табылатын болса, онда бастапқы моментке t _o бастапқы шарттар деп аталатын кейбір шарттар қойылады. Берілген бастапқы шарттар кезіндегі теңдеудің шешімінде тұратын есеп, дербес туындылы теңдеулер үшін Коши есебі деп аталады. Сонымен қатар есебіміз шексіз кеңістікте шешіледі және шекара шарттары қойылмайды. Қалыптасуы кезінде бастапқы және шекара шарттары қойылатын есептер стационар емес шектік есептер деп аталады. Осы кезде алынған шешім уақыт өтуімен өзгереді.

Алдағы уақытта тек нақты қойылған есептерді қарастыратын боламыз, яғни кейбір кластағы бастапқы және шекара шарттарында шешімі бар және ол жалғыз болатын.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.